Как построить правильную шестиугольную призму

Как научиться правильно изображать призму

Главная страница » Основы Академического рисунка » Как построить призму. Правильное изображение фигуры на рисунке

Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.

В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.

Рисуем четырехгранную призму

Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.

Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).

Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.

Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.

Шестигранная призма

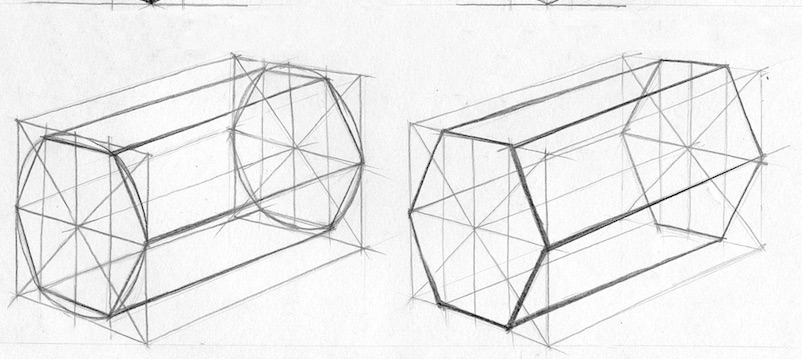
Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.

Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.

Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.

Зачем уметь строить эту геометрическую фигуру?

Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.

С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.

Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.

Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.

В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.

Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.

Источник

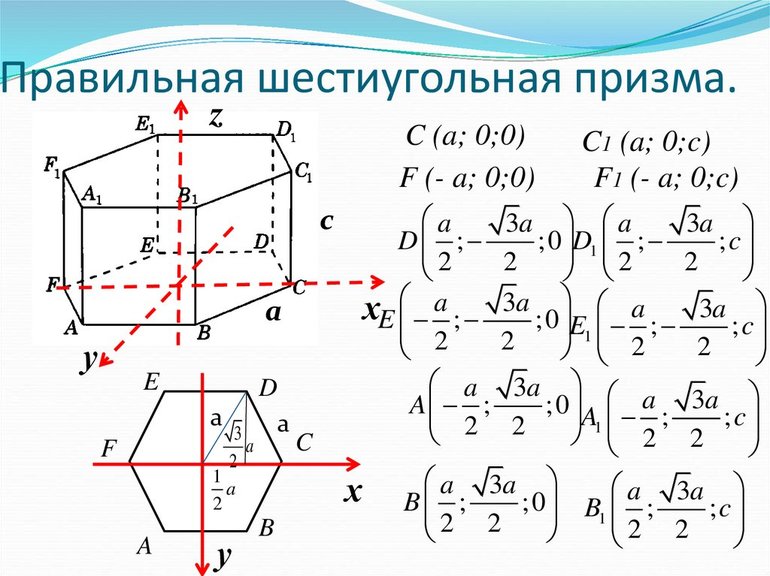
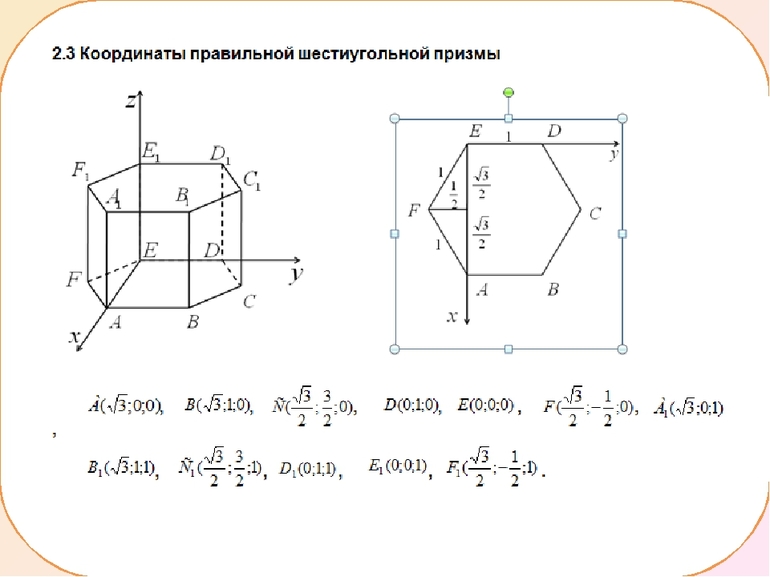
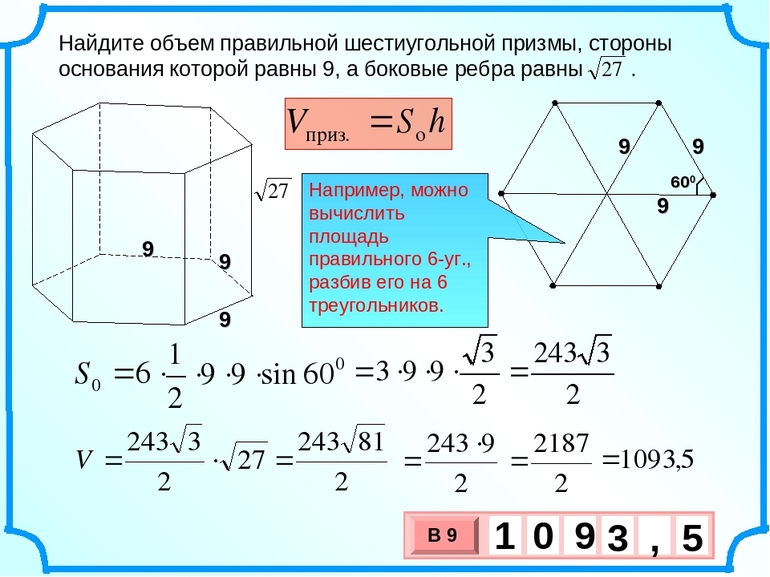
Правильная шестиугольная призма

Шестиугольная призма — это многогранник, две грани которого являются равными шестиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.

Основания призмы являются равными правильными шестиугольниками.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности шестиугольной призмы:

Источник

Презентация «Аксонометрические проекции. Диметрия правильной шестигранной призмы»

Аксонометрические построения Автор презентации: учитель Изо и черчения ГБОУ школы №93 Столяренко Юлиана Федоровна.

Вопросы для повторения Фамилия имя____________________ класс___________________________________ 1. Какие виды аксонометрических проекций вы знаете? 2. Чем они отличаются? 3. Под какими углами располагаются оси в диметрии? 4. Под какими углами располагаются оси в изометрии? 5. Какая ось всегда вертикальна? 6. Как с помощью клеточек отложить угол в 30 градусов?

Задача: Построить фронтальную диметрическую проекцию правильной шестиугольной призмы С чего начнем построение? 2. Размеры: основание призмы вписано в окружность радиусом R 20, высота призмы 45 мм (достаточно ли этих размеров для построения?)

Построение Вычерчиваем основание призмы – правильный шестигранник вписанный в окружность R 20

Построение Чертим окружность R 20

Построение Проводим оси через центр окружности

Построение Начиная с точки пересечения оси и окружности радиусом R 20 ставим засечки по окружности

Построение Из точки пересечения оси и окружности тем же радиусом ставим засечки на окружности

Построение Соединяем точки разметки на окружности

Построение Соединяем точки разметки на окружности получаем правильный шестигранник вписанный в окружность радиусом R20

Построение Нумеруем вершины правильного шестигранника

Построение Сверху построим оси для фронтальной диметрической проекции

Построение Вверху листа построим оси для фронтальной диметрической проекции (ось У под углом 45 градусов)

Построение Продлить ось У под углом 45о градусов в другую сторону от (.)0

Построение Отметить ось У и ось Х точку 0 на чертеже основания

Построение Взять раствор циркуля равный радиусу по оси ОХ от 0 до точки 3

Построим основание в диметрии Отметить раствором R20 засечки по оси ОХ от (.)0 до точки 3 и в противоположную сторону до точки 7 (или линейкой отложив размер в натуральную величину)

Построение Линейкой измерить расстояние по оси ОУ от 0 до точки 5 (вычислить размер для диметрии поделив натуральную величину на 2)

Построение Отложить полученный размер по оси ОУ от 0 до точки 4 и в противоположную сторону до точки 1 поставить нумерацию точек

Построение Провести линии параллельные оси ОХ через точку 4 и точку 1

Построение Измерить расстояние от точки 5 до точки 4 отложить его на аксонометрическом чертеже

Построение Измерить расстояние от точки 5 до точки 4 отложить его на аксонометрическом чертеже то же до точки 6, и то же до точки 1 и до точек 2, 8.

Построение Соединить точки 6 и7, точки 3 и 2, и далее последовательно все точки шестигранника.

Построение Поднять высоты из точек основания шестигранника на высоту h = 45 (мм), соединить точки верхнего основания.

Построение Получилась правильная шестигранная призма высотой 45 мм.

Домашнее задание Построить в диметрии и изометрии правильную шестигранную пирамиду с основанием вписанным в окружность R=20 высотой 45 мм.

Источник

Линейно-конструктивный рисунок шестигранной призмы

ЦЕЛЬ ЗАДАНИЯ. Научиться изображать шести­гранную призму в различных положениях.

ПОСТАНОВКА ЗАДАНИЯ. Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольни­ков постройте шестигранные призмы.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основа­нии шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — оди­наковые прямоугольники. Для того, чтобы правиль­но изобразить шестигранник в перспективе, необ­ходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифра­ми от одного до шести.

Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности де­лят диаметр 5— 2 на четыре равных отрезка (эти от­резки обозначены дугами). Противоположные сто­роны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяю­щей две вершины (например, стороны 6— 1 и 4— 3 параллельны прямой 5— 2). Эти наблюдения помо­гут вам построить шестиугольник в перспективе, а также проверить правильность этого построения.
Построить правильный шестиугольник по представ­лению можно двумя способами: на основе описан­ной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольни­ка принадлежат описанной окружности, радиус ко­торой равен стороне шестиугольника.

Горизонтальный шестиугольник

Изобразите го­ризонтальный эллипс произвольного раскрытия, т.е. описанную окружность в перспективе. Теперь необ­ходимо найти на ней шесть точек, являющихся вер­шинами шестиугольника. Проведите любой диа­метр данной окружности через ее центр (рис. 3.57).
Крайние точки диаметра — 5 и 2, лежащие на эллип­се, являются вершинами шестиугольника. Для на­хождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диа­метр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус попо­лам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины ради­усов — точки А и В — прямые, перпендикулярные пря­мой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В парал­лельно этим касательным, будут также перпендику­лярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямы­ми линиями (рис. 3.61).

Проверьте правильность вашего построения разными способами. Если построение верно, то ли­нии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шести­угольника параллельны соответствующим диамет­рам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.

Вертикальный шестиугольник

В таком шести­угольнике прямые, соединяющие точки 1 и 3, 6 и 4, а также касательные к описанной окружности в точ­ках 5 и 2, имеют вертикальное направление и сохра­няют его на перспективном рисунке. Таким обра­зом, проведя две вертикальные касательные к эл­липсу, найдем точки 5 и 2 (точки касания). Соедини­те их прямой линией, а затем разделите полученный диаметр 5— 2 на 4 равных отрезка, учитывая их пер­спективные сокращения (рис. 3.65). Проведите вер­тикальные прямые через точки А и В, а на их пере­сечении с эллипсом найдите точки 7, 3, 6 и 4. Затем последовательно соедините точки 1— 6 прямыми (рис. 3.66). Правильность построения шестиуголь­ника проверьте аналогично предыдущему примеру.

Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружно­сти, изобразить которую в перспективе проще, чем
квадрат заданных пропорций. Поэтому данный спо­соб построения шестиугольника представляется наиболее точным и универсальным. Способ постро
ения на основе квадрата позволяет легко изобра­зить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизон­тальному направлению 5— 2 равен стороне квадра­та, а по вертикали — меньше ее длины.

Вертикальный шестиугольник

Нарисуйте вер­тикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5— 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68).
Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изоб­разите их на некотором расстоянии (1/14 а) от гори­зонтальных сторон квадрата и параллельно им. Со­единив найденные таким образом точки 1 и 3 с точ­кой 2, а точки 6 и 4 — с точкой 5, получим шести­угольник (рис. 3.69).

Гэризонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).

Этот способ построения уместен только для ше­стиугольников с достаточным раскрытием. В слу­чае, если раскрытие шестиугольника незначитель­но, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиуголь­ника, построенного через квадрат, можно использо­вать уже известные вам методы.

Кроме того существует еще один — описать вок­руг полученного шестиугольника окружность (на ва­шем рисунке — эллипс). Все вершины шестиуголь­ника должны принадлежать этому эллипсу.

Овладев навыками изображения шестиугольни­ка, вы свободно перейдете к изображению шести­гранной призмы. Внимательно рассмотрите схему
на рис. 3.72, а также схемы построения шестигран­ных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78).

Изобразите вертикальные и горизон­тальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке гори­зонтального шестигранника длинные стороны боко­вых граней будут сходиться в точке схода на гори­зонте, а раскрытие шестиугольника основания бу­дет тем больше, чем дальше от зрителя он находит­ся. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходи­лись в перспективе (рис. 3.79; 3.80).

Источник

Общие сведения

Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.

Кроме основания и граней, в состав стереофигуры входит:

Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.

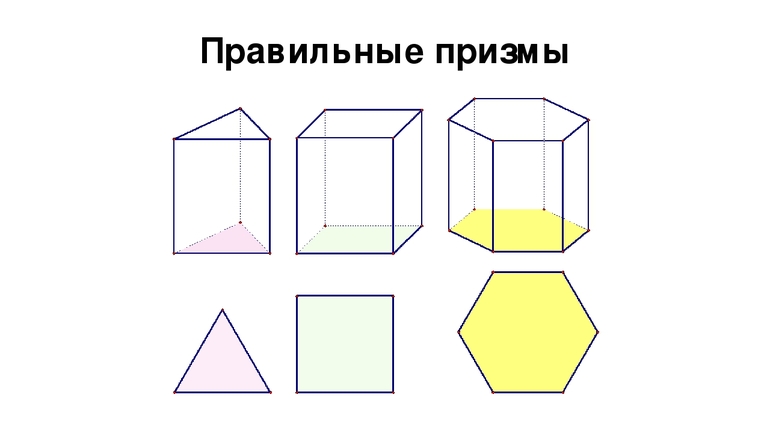
В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.

Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.

Свойства шестигранника

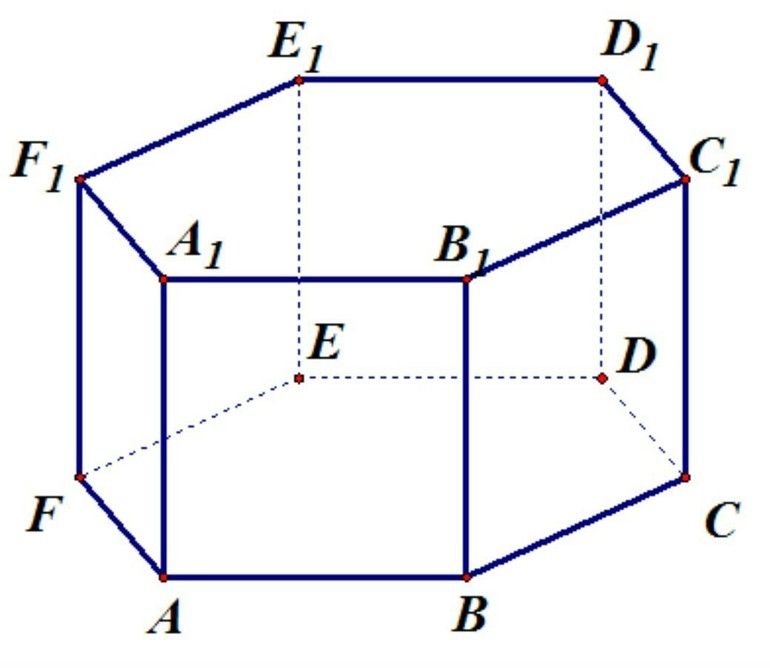
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.

Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.

По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1 2 + AE 2 )= √(h 2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1 2 + BE 2 ) = √(h 2 + 4 *a) = √5 *a. Сторона FE1 = √(FE 2 + EE 2 ) = √(h 2 + a 2 ) = √2 *a.

Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h 2 + a 2 ), что и следовало доказать.

Решение простого примера

Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.

Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.

Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.

Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.

С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.

Задача высокого уровня

Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.

Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

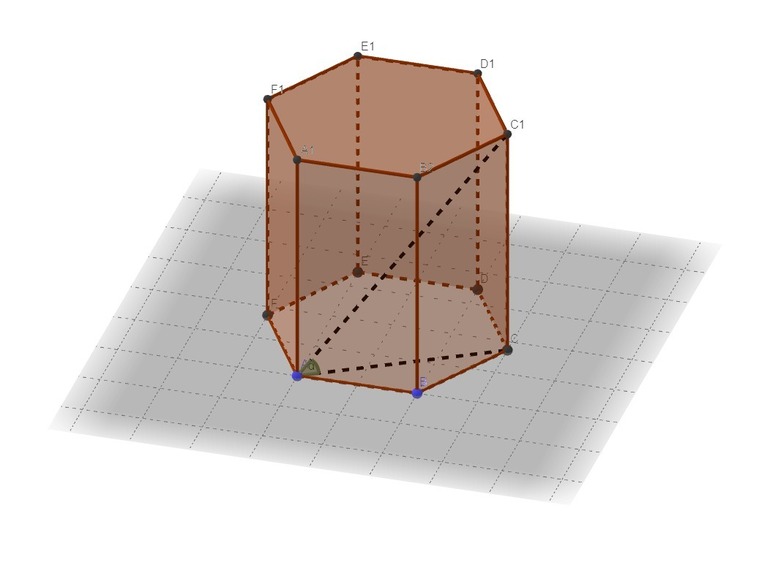
В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.

Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.

Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.

Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R 2 = (12 * 2) / 3 √ 3 = 8 /√3.

Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a 2 * sin60 / 2 = (R 2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.

Источник