Как построить плоскость перпендикулярную прямой

Как построить плоскость перпендикулярную прямой

Контрольные задания по теме: Рабочая тетрадь задача 44, задача 45

Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.

Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.

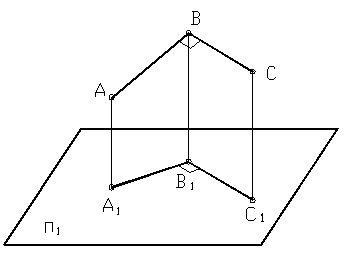
Рисунок 28

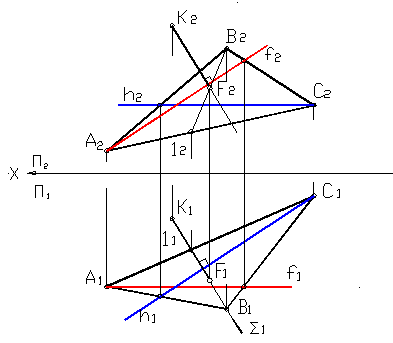
Рисунок 29

На рисунке 29 изображено построение перпендикуляра КF к плоскости АВС.

Две плоскости перпендикулярны, если прямая, лежащая в одной плоскости, перпендикулярна двум пересекающимся прямым другой плоскости. Построение плоскости перпендикулярной данной плоскости АВС показано на рисунке 30. Через точку М проводится прямая МN, перпендикулярная плоскости АВС. Горизонтальная проекция этой прямой перпендикулярна АС, так как АС является горизонталью, а фронтальная проекция перпендикулярна АВ, так как АВ – фронталь. Затем через точку М проводится произвольная прямая EF. Таким образом, плоскость перпендикулярна АВС и задана двумя пересекающимися прямыми EF и MN.

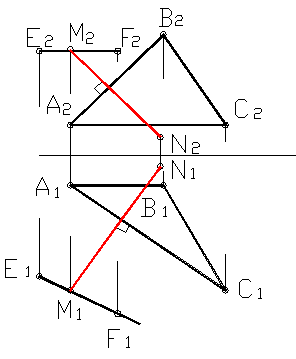
Рисунок 30

Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.

Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.

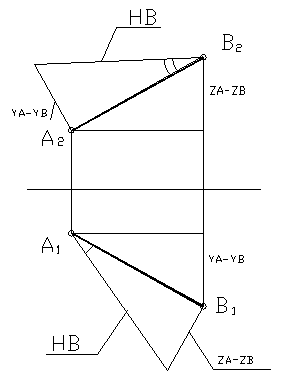
Рисунок 31

1. Сформулируйте теорему о свойстве прямого угла.

2. В каком случае прямая перпендикулярна плоскости?

3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства?

4. Для чего применяется способ прямоугольного треугольника?

5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Как построить плоскость перпендикулярную прямой

Контрольные задания по теме: Рабочая тетрадь задача 44, задача 45

Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.

Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.

Рисунок 28

Рисунок 29

На рисунке 29 изображено построение перпендикуляра КF к плоскости АВС.

Две плоскости перпендикулярны, если прямая, лежащая в одной плоскости, перпендикулярна двум пересекающимся прямым другой плоскости. Построение плоскости перпендикулярной данной плоскости АВС показано на рисунке 30. Через точку М проводится прямая МN, перпендикулярная плоскости АВС. Горизонтальная проекция этой прямой перпендикулярна АС, так как АС является горизонталью, а фронтальная проекция перпендикулярна АВ, так как АВ – фронталь. Затем через точку М проводится произвольная прямая EF. Таким образом, плоскость перпендикулярна АВС и задана двумя пересекающимися прямыми EF и MN.

Рисунок 30

Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.

Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.

Рисунок 31

1. Сформулируйте теорему о свойстве прямого угла.

2. В каком случае прямая перпендикулярна плоскости?

3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства?

4. Для чего применяется способ прямоугольного треугольника?

5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Как построить плоскость перпендикулярную прямой

Признак перпендикулярности прямой и плоскости позволяет построить взаимно перпендикулярные прямую и плоскость, т. е. доказать существование таких прямых и плоскостей. Начнем с построения плоскости, перпендикулярной данной прямой и проходящей через данную точку. Решим две задачи на построение, соответствующие двум возможностям в расположении данной точки и данной прямой.

Задача 1. Через данную точку А на данной прямой a провести плоскость, перпендикулярную этой прямой.

Проведем через прямую а любые две плоскости и в каждой их этих плоскостей через точку А проведем по прямой, перпендикулярной прямой а, обозначим их b и с (рис. 2.17). Плоскость а, проходящая через прямые бис, содержит точку А и перпендикулярна прямой а (по признаку перпендикулярности прямой и плоскости). Поэтому плоскость а искомая. Задача решена.

Итак, предположив, что через точку А проходят две плоскости, перпендикулярные прямой а, мы пришли к противоречию. Поэтому задача имеет единственное решение.

Задача 2. Через данную точку А, не лежащую на данной прямой а, провести плоскость, перпендикулярную этой прямой.

Через точку А проводим прямую b, перпендикулярную прямой а. Пусть В — точка пересечения а и b. Через точку В проводим еще прямую с, перпендикулярную прямой а (рис. 2.19). Плоскость, проходящая через обе проведенные прямые, будет перпендикулярна а по признаку перпендикулярности (теорема 2).

Как и в задаче 1, построенная плоскость единственная. Действительно, возьмем любую плоскость, проходящую через точку А перпендикулярно прямой а. Такая плоскость содержит прямую, перпендикулярную прямой а и проходящую через точку А. Но такая прямая только одна. Это прямая b, которая проходит через точку В. Значит, плоскость, проходящая через А и перпендикулярная прямой а, должна содержать точку В, а через точку В проходит лишь одна плоскость, перпендикулярная прямой а (задача 1). Итак, решив эти задачи на построение и доказав единственность их решений, мы доказали следующую важную теорему.

Теорема 3 (о плоскости, перпендикулярной прямой). Через каждую точку проходит плоскость, перпендикулярная данной прямой, и притом только одна.

Следствие (о плоскости перпендикуляров). Прямые, перпендикулярные данной прямой в данной ее точке, лежат в одной плоскости и покрывают ее.

крыта прямыми, перпендикулярными прямой а в точке А, т.е. через каждую точку плоскости а в ней проходит прямая, перпендикулярная прямой а.

Пример к следствию теоремы 3 дают спицы в колесе, перпендикулярные его оси: при вращении они зачерчивают плоскость (точнее, круг), принимая все положения, перпендикулярные оси вращения.

Теоремы 2 и 3 помогают дать простое решение следующей задачи.

Задача 3. Через точку данной плоскости провести прямую, перпендикулярную этой плоскости.

Пусть даны плоскость а и точка А в плоскости а. Проведем в плоскости а через точку А какую-либо прямую а. Через точку А проведем плоскость , перпендикулярную прямой а (задача 1). Плоскость пересечет плоскость а по некоторой прямой b (рис. 2.21). Проведем в плоскости Р через точку А прямую с, перпендикулярную прямой b. Так как (поскольку с лежит в плоскости

и ), то по теореме 2 . Единственность ее решения установлена в п. 2.1.

Замечание. О построениях в пространстве. Напомним, что в главе 1 мы изучаем «строительную геометрию». А в этом пункте мы решили три задачи на построение в пространстве. Что же понимают в стереометрии под терминами «построить”, «провести», «вписать» и т.п.? Сначала вспомним о построениях на плоскости. Указав, например, как строить окружность, описанную около треугольника, мы тем самым доказываем ее существование. Вообще, решая задачу на построение, мы доказываем теорему существования фигуры с заданными свойствами. Это решение сводится к составлению некоторого алгоритма построения искомой фигуры, т.е. к указанию последовательности выполнения простейших операций, приводящих к необходимому результату. Простейшие операции — это проведение отрезков, окружностей и нахождение точек их пересечения. Затем с помощью чертежных инструментов выполняется непосредственное построение фигуры на бумаге или на доске.

Итак, в планиметрии решение задачи на построение имеет как бы две стороны: теоретическую — алгоритм построения — и практическую — реализацию этого алгоритма, например, циркулем и линейкой.

У стереометрической задачи на построение остается лишь одна сторона — теоретическая, так как нет инструментов для построения в пространстве, аналогичных циркулю и линейке.

За основные построения в пространстве принимают те, которые обеспечиваются аксиомами и теоремами о существовании прямых и плоскостей. Это — проведение прямой через две точки, проведение плоскости (предложения п. 1.1 и аксиома 1 п. 1.4), а также построение прямой пересечения любых двух построенных плоскостей (аксиома 2 п. 1.4). Кроме того, мы, естественно, будем считать, что можно выполнять планиметрические построения в уже построенных плоскостях.

Решить задачу на построение в пространстве — это значит указать последовательность основных построений, в результате которых получается нужная фигура. Обычно явно указываются не все основные построения, а делаются ссылки на уже решенные задачи на построение, т.е. на уже доказанные предложения и теоремы о возможности таких построений.

Кроме построений — теорем существования в стереометрии, возможны еще два вида задач, связанных с построениями.

Во-первых, задачи на рисунке или на чертеже. Таковы задачи на сечения многогранников или других тел. Мы не строим на самом деле само сечение, а только изображаем его на

рисунке или чертеже, который у нас уже есть. Такие построения осуществляются как планиметрические с учетом аксиом и теорем стереометрии и правил изображений. Задачи такого типа постоянно решают в черчении и в конструкторской практике.

Во-вторых, задачи на построение на поверхностях тел. Задача: «Построить точки на поверхности куба, удаленные от данной его вершины на данное расстояние» — решается с помощью циркуля (как?). Задача: «Построить точки на поверхности шара, удаленные от данной точки на данное расстояние» — также решается с помощью циркуля (как?). Задачи такого типа решают не на уроках геометрии — их постоянно решает разметчик, разумеется, с точностью, которой позволяют добиться его инструменты. Но, решая такие задачи, он опирается на геометрию.

Источник

Построение плоскости перпендикулярной к прямой

Провести через точку С плоскость Р, перпендикулярную к прямой АВ.

Поскольку фронтальная проекция прямой АВ параллельна оси проекций ОХ, искомая плоскость будет горизонтально-проектирующей – во фронтальной плоскости след плоскости Р будет перпендикулярным оси ОХ.

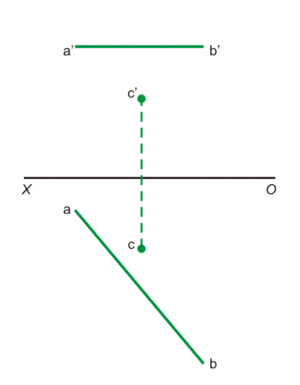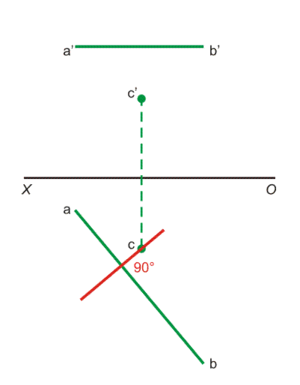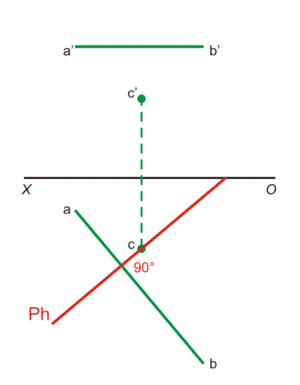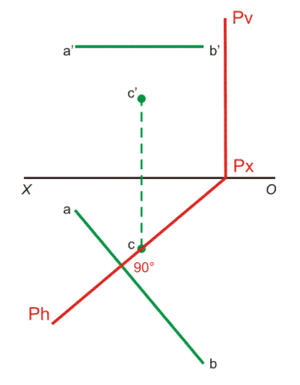
Поэтому построить надо только горизонтальный след плоскости Р, проходящий через вертикальную проекцию точки С и перпендикулярный вертикальной проекции прямой АВ.

Горизонтальный след плоскости Р – перпендикуляр из точки пересечения вертикального следа плоскости Р с осью проекций.

Исходная статья

Литература

Х. А. Арустамов «Сборник задач по начертательной геометрии», М., 1971 г.

Полезное

Смотреть что такое «Построение плоскости перпендикулярной к прямой» в других словарях:

Построение плоскости перпендикулярной к прямой (2) — Дано. Прямая АВ и точка С. Требуется. Провести через точку С плоскость Р, перпендикулярную к прямой АВ. Решение. Поскольку и горизонтальная и вертикальная проекции прямой АВ перпендикулярны оси проекций ОХ, любая плоскость со следами… … Википедия

Перпендикуляр — Перпендикулярность бинарное отношение между различными объектами (векторами, прямыми, подпространствами и. т. д.) в евклидовом пространстве. Частный случай ортогональности. Содержание 1 Перпендикулярность прямых на плоскости … Википедия

Свет* — Содержание: 1) Основные понятия. 2) Teopия Ньютона. 3) Эфир Гюйгенса. 4) Принцип Гюйгенса. 5) Принцип интерференции. 6) Принцип Гюйгенса Френеля. 7) Принцип поперечности колебаний. 8) Завершение эфирной теории света. 9) Основание эфирной теории.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Свет — Содержание: 1) Основные понятия. 2) Теория Ньютона. 3) Эфир Гюйгенса. 4) Принцип Гюйгенса. 5) Принцип интерференции. 6) Принцип Гюйгенса Френеля. 7) Принцип поперечности колебаний. 8) Завершение эфирной теории света. 9) Основание эфирной теории.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ГОСТ 22268-76: Геодезия. Термины и определения — Терминология ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа: 114. Абрис Ндп. Кроки D. Gelandeskizze Gelandekroki E. Outline Field sketch F. Croquis Схематический чертеж участка местности Определения термина из разных документов … Словарь-справочник терминов нормативно-технической документации

Начертательная геометрия — раздел геометрии, в котором пространственные фигуры изучаются при помощи построения их изображений на плоскости, в частности построения проекционных изображений, а также методы решения и исследования пространственных задач на плоскости.… … Большая советская энциклопедия

МИКРОСКОП — (от греч. mikros малый и skopeo смотрю), оптический инструмент для изучения малых предметов, недоступных непосредственному рассмотрению невооруженным глазом. Различают простой М., или лупу, и сложный М., или микроскоп в собственном смысле. Лупа… … Большая медицинская энциклопедия

Двойное лучепреломление — Прозрачный кристалл минерала, называемого исландским шпатом (известковый шпат, кальцит), будучи положен на рисунок или чертеж, показывает их линии раздвоенными. Покрывая одну грань такого кристалла непрозрачной пластинкой, в которой сделан… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Часы прибор для измерения времени — Содержание: 1) Исторический очерк развития часовых механизмов: а) солнечные Ч., b) водяные Ч., с) песочные Ч., d) колесные Ч. 2) Общие сведения. 3) Описание астрономических Ч. 4.) Маятник, его компенсация. 5) Конструкции спусков Ч. 6) Хронометры … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Часы — Содержание. 1) Исторический очерк развития часовых механизмов: а) солнечные Ч., b) водяные Ч., с) песочные Ч., d) колесные Ч. 2) Общие сведения. 3) Описание астрономических Ч. 4.) Маятник, его компенсация. 5) Конструкции спусков Ч. 6) Хронометры … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Как построить плоскость перпендикулярную прямой

Из всех возможных положений прямой, пересекающей плоскость, отметим случай, когда прямая перпендикулярна к плоскости, и рассмотрим свойства проекций такой прямой.

На рис. 185 задана плоскость, определяемая двумя пересекающимися прямыми AN и AM, причем AN является горизонталью, а AM — фронталью этой плоскости. Прямая АВ, изображенная на том же чертеже, перпендикулярна к AN и к AM и, следовательно, перпендикулярна к определяемой ими плоскости.

Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости. Но чтобы при этом проекция перпендикуляра к плоскости общего положения оказалась перпендикулярной к одноименной проекции какой-либо прямой этой плоскости, прямая должна быть горизонталью, или фронталью, или профильной прямой плоскости. Поэтому, желая построить перпендикуляр к плоскости, берут в общем случае две такие прямые (например, горизонталь и фронталь, как это показано на рис. 185).

Итак, у перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проекции фронтали, профильная проекция перпендикулярна к профильной проекции профильной прямой этой плоскости.

Очевидно, в случае, когда плоскость выражена следами (рис. 186), мы получаем следующий вывод: если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна к горизонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоскости.

Итак, если в системе π₁ п₂ горизонтальная проекция прямой перпендикулярна к горизонтальному следу и фронтальная проекция прямой перпендикулярна к фронтальному следу плоскости, то в случае плоскостей общего положения (рис. 186), а также горизонтально и фронтально-проецирующих прямая перпендикулярна к плоскости. Но для профильно-проецирующей плоскости может оказаться, что прямая к этой плоскости не перпендикулярна, хотя проекции прямой соответственно перпендикулярны к горизонтальному и фронтальному следам плоскости. Поэтому в случае профильно-проецирующей плоскости надо рассмотреть также взаимное положение профильной проекции прямой и профильного следа данной плоскости и лишь после этого установить, будут ли перпендикулярны между собой данные прямая и плоскость.

Очевидно (рис. 187), горизонтальная проекция перпендикуляра к плоскости сливается с горизонтальной проекцией линии ската, проведенной в плоскости через основание перпендикуляра.

На рис. 188 показано построение перпендикуляра к плоскости, определяемой треугольником АВС. Перпендикуляр проведен через точку А.

Так как фронтальная проекция перпендикуляра к плоскости должна быть перпендикулярна к фронтальной проекции фронтали плоскости, а его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, то в плоскости через точку А проведены фронталь с проекциями A’D’ и A»D» и горизонталь А»Е», А’Е’. Конечно, эти прямые не обязательно проводить именно через точку А.

Далее проведены проекции перпендикуляра: M»N» ⊥ A»D», M’N’ ⊥ А’Е’. Почему проекции на рис. 188 на участках A»N» и А’М’ показаны штриховыми линиями? Потому, что здесь рассматривается плоскость, заданная треугольником АВС, а не только этот треугольник: перпендикуляр находится частично перед плоскостью, частично за ней.

На рис. 189 и 190 показано построение плоскости, проходящей через точку А перпендикулярно к прямой ВС. На рис. 189 плоскость выражена следами. Построение начато с проведения через точку А горизонтали искомой плоскости: так как горизонтальный след плоскости должен быть перпендикулярен к В’С’ то и горизонтальная проекция горизонтали должна быть перпендикулярна к В’С’. Поэтому A’N’ ⊥ В’С. Проекция A»N» || оси х, как это должно быть у горизонтали. Затем проведен через точку N» (N» — фронтальная проекция фронтальною следа горизонтали AN) след f’_0a ⊥ »ѻ, получена точка Х_a и проведен след h’_0a || A’N’ (h’_0a ⊥ В’С’).

На рис. 190 плоскость определена ее фронталью AM и горизонталью AN. Эти прямые перпендикулярны к ВС (А»М» ⊥ »ѻ, A’N’ ⊥ В’С); определяемая ими плоскость перпендикулярна к ВС.

Так как перпендикуляр к плоскости перпендикулярен к каждой прямой, проведенной в этой плоскости, то, научившись проводить плоскость перпендикулярно к прямой, можно воспользоваться этим для проведения перпендикуляра из некоторой точки А к прямой общего положения ВС. Очевидно, можно наметить следующий план построения проекций искомой прямой:

1) через точку А провести плоскость (назовем ее ϒ), перпендикулярную к ВС;

2) определить точку К пересечения прямой ВС с пл. ϒ;

3) соединить точки А и К отрезком прямой линии.

Прямые АК и ВС взаимно перпендикулярны.

Пример построения дан на рис. 191. Через точку А проведена плоскость (ϒ), перпендикулярная к ВС. Это сделано при помощи фронтали, фронтальная проекция A»F» которой проведена перпендикулярно к фронтальной проекции »ѻ и горизонтали, горизонтальная проекция которой перпендикулярна к В’С’.

Затем найдена точка К, в которой прямая ВС пересекает пл. ϒ. Для этого через прямую ВС проведена горизонтально-проецируюшая плоскость β (на чертеже она задана только горизонтальным следом β’). Пл. β пересекает пл. ϒ по прямой с проекциями 1’2‘ и 1″2″. В пересечении этой прямой с прямой ВС получается точка К. Прямая АК является искомым перпендикуляром к ВС. Действительно, прямая АК пересекает прямую ВС и находится в пл. ϒ, перпендикулярной к прямой ВС; следовательно, АК ⊥ ВС.

На рис. 192 изображены плоскость общего положения а, проходящая через точку А, и перпендикуляр AM к этой плоркости, продолженный до пересечения с пл. п₁, в точке В’.

Угол ф₁ между пл. а и пл. п₁ и угол ф между прямой AM и пл. п₁ являются острыми углами прямоугольного треугольника В’АМ’ и, следовательно, ф₁ +ф = 90°. Аналогично, если пл. а составляет с пл. п₂ угол σ₂, а прямая AM, перпендикулярная к а, составляет с пл. п₂ угол σ, то σ₂ + σ = 90°. Из этого, прежде всего, следует, что плоскость общею положения, которая должна составлять с пл. п₁ угол ф₁ а с пл. п₂ угол σ₂, может быть построена, лишь если 180° > Ф₁ + σ2 > 90°.

Действительно, складывая почленно Ф₁ + Ф = 90° и σ₂ + σ = 90°, получим Ф₁ + σ₂ + Ф + σ = 180°, т. е. Ф₁ + σ₂ 90°. Если взять Ф₁ + σ₂ =90°, то получится профильно-проецирующая плоскость, а если взять Ф₁ + σ₂ = 180°, то получится профильная плоскость, т. е. в обоих этих случаях плоскость не общего положения, а частного.

ПОСТРОЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЕЙ

Построение плоскости β, перпендикулярной к плоскости a, может быть произведено двумя путями: 1) пл. β проводится через прямую, перпендикулярную к пл. а; 2) пл. β проводится перпендикулярно к прямой, лежащей в пл. а или параллельной этой плоскости. Для получения единственного решения требуются дополнительные условия.

На рис. 193 показано построение плоскости, перпендикулярной к плоскости, заданной треугольником CDE. Дополнительным условием здесь служит то, что искомая плоскость должна проходить через прямую А В. Следовательно, искомая плоскость определяется прямой АВ и перпендикуляром к плоскости треугольника. Для проведения этого перпендикуляра к пл. CDE в ней взяты фронталь CN и горизонталь СМ: если B»F» ⊥ C“N» и B’F’⊥C’M’, то BF⊥ пл. CDE.

Образованная пересекающимися прямыми АВ и BF плоскость перпендикулярна к пл. СОЕ, так как проходит через перпендикуляр к этой плоскости. На рис. 194 горизонтально-проецирующая плоскость β проходит через точку К перпендикулярно к плоскости, заданной треугольником АВС. Здесь дополнительным условием являлась перпендикулярность искомой плоскости сразу к двум плоскостям: к пл. АВС и к пл. п₁. Поэтому и ответом служит горизонтально-проецирующая плоскость. А так как она проведена перпендикулярно к горизонтали AD, т. е. к прямой, принадлежащей пл. АВС, то пл. β перпендикулярна к пл. АВС.

Может ли перпендикулярность одноименных следов плоскостей служить признаком перпендикулярности самих плоскостей?

К очевидным случаям, когда это так, относится взаимная перпендикулярность двух горизонтально-проецирующих плоскостей, у которых горизонтальные следы взаимно перпендикулярны. Также это имеет место при взаимной перпендикулярности фронтальных следов фронтально-проецирующих плоскостей; эти плоскости взаимно перпендикулярны.

Рассмотрим (рис. 195) горизонтально-проецирующую плоскость β, перпендикулярную к плоскости общего положения а.

Итак, перпендикулярность горизонтальных следов плоскости общего положения и горизонтально-проецирующей соответствует взаимной перпендикулярности этих плоскостей.

Очевидно, перпендикулярность фронтальных следов фронтально-проецирующей плоскости и плоскости общего положения также соответствует взаимной перпендикулярности этих плоскостей.

Но если одноименные следы двух плоскостей общего положения взаимно перпендикулярны, то самые плоскости не перпендикулярны между собой, так как здесь не соблюдается ни одно из условий, изложенных в начале этого параграфа.

В заключение рассмотрим рис. 196. Здесь имеет место случай взаимной перпендикулярности одноименных следов в обеих их парах и перпендикулярности самих плоскостей: обе плоскости особого (частного) положения — профильная ϒ и профильно-проецирующая а.

Источник