Как построить плоскость параллельную прямой

Лекция 3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

\left.\begin\alpha=m\parallel n,\\D\in\alpha\\C\in\alpha\\\end\right\> \Longrightarrow CD\in\alpha

Упражнение

Рисунок 3.7 – Решение задачи

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

\alpha=m\cap n\\\left.\begina_2\parallel m_2\\a_1\parallel m_1\\\end\right\> \Rightarrow a\parallel\alpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Упражнение

Алгоритм решения задачи :

\left.\beginAB\cap\sigma=K\\AC\cap\sigma=L\\\end\right\> \left.\begin\Rightarrow A_1B_1\cap\sigma_1=K_1 \rightarrow K_2\\\Rightarrow A_1C_1\cap \sigma_1=L_1 \rightarrow L_2\\\end\right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

\left.\begin\alpha\cap\sigma=(4-5)\\\beta\cap\sigma=(3-2)\\\end\right\>\\\left.\begin\alpha\cap\tau=(6-7)\\\beta\cap\tau=(1-8)\\\end\right\>\left.\begin(4_1-5_1)\cap(3_1-2_1)=M_1\rightarrow M_2\\(6_1-7_1)\cap(1_1-8_1)=N_1\rightarrow N_2\\\end\right\>\rightarrow\\\left.\beginM_1N_1\\M_2N_2\\\end\right\>\Rightarrow\alpha\cap\beta=MN

Упражнение

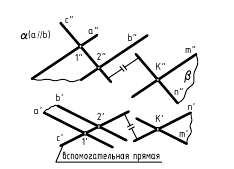
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Источник

Как построить плоскость параллельную прямой

Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:

1. тремя точками, не лежащими на одной прямой линии (рис. 41 );

Рисунок 41. Плоскость, заданная тремя точками, не лежащими на одной прямой

2. прямой линией и точкой, не принадлежащей этой прямой (рис. 4 2);

Рисунок 42. Плоскость, заданная прямой линией и точкой, не принадлежащей этой линии

3. двумя пересекающимися прямыми (рис.43);

Рисунок 43. Плоскость, заданная двумя пересекающимися прямыми

4. двумя параллельными прямыми (рис.44);

Рисунок 44. Плоскость, заданная двумя п араллельны ми прямы ми

5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).

С ледом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a _П1, фронтальный a _П2 и профильный a _П3 следы.

Рисунок 45. Плоскость, заданная следами

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.

Источник

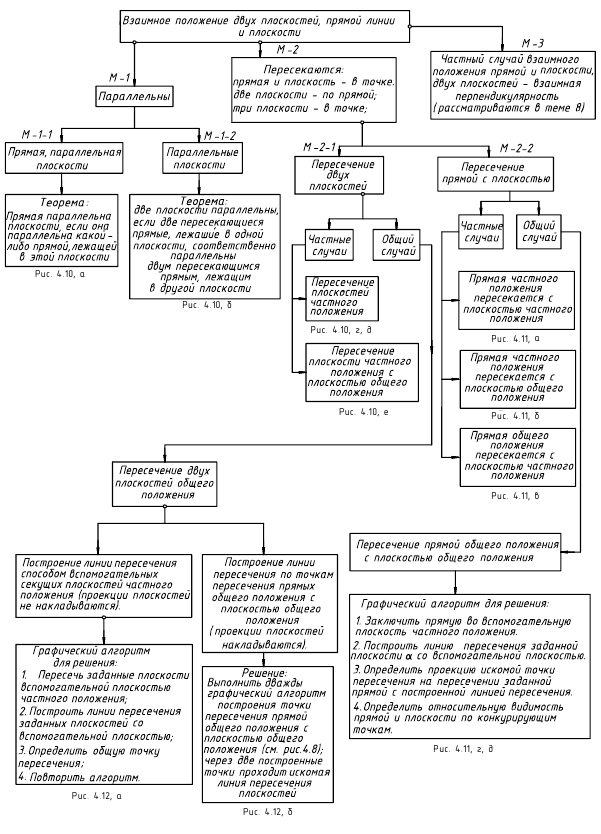
Взаимное положение двух плоскостей, прямой линии и плоскости с примерами

Содержание:

Взаимное положение двух плоскостей, прямой линии и плоскости:

Плоскости в пространстве могут быть параллельными или пересекающимися.

Из геометрии известно: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Следовательно, на чертеже у параллельных плоскостей должны быть соответственно параллельны одноименные проекции двух пересекающихся прямых, лежащих в каждой из плоскостей. Этот признак параллельных плоскостей используется для определения на чертеже параллельности двух заданных плоскостей и построения параллельных плоскостей.

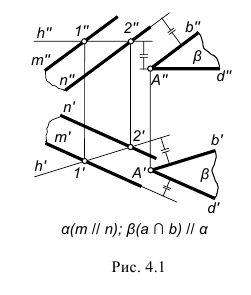
На рис. 4.1 показано построение плоскости β, проведенной через заданную точку А(A»‘A’), параллельно заданной плоскости α(m//n).

Для решения задачи следует выполнить следующие графические действия:

1-е действие. В заданной плоскости α, построить вспомогательную прямую, например, горизонталь h(h»h’), то есть создать в плоскости пересекающиеся прямые.

2-е действие. Через заданную точку А(A»‘A’) провести две пересекающиеся прямые b и d, параллельные двум пересекающимся прямым m и h заданной плоскости α:

Построенная плоскость β(b∩d) будет параллельна заданной плоскости α(m//n), так как две пресекающиеся прямые m и h плоскости α соответственно параллельны двум пересекающимся прямым b и d построенной плоскости β.

Параллельность прямой и плоскости

Из геометрии известно: прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. Следовательно, на чертеже (рис. 4.1) прямая, например, b параллельна плоскости α(m//n), так как проекции прямой b проведены параллельно одноименным проекциям прямой m(m»,m’), лежащей в этой плоскости.

Плоскости пересекающиеся

Общим элементом пересечения двух плоскостей является прямая линия, принадлежащая обеим плоскостям.

Плоскости, как известно, могут занимать частные и общее положения относительно плоскостей проекций, и поэтому при пересечении двух плоскостей возможны три случая:

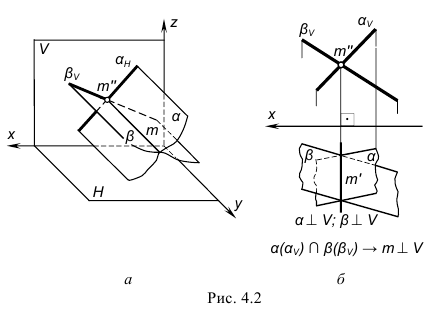
1-й случай – обе плоскости занимают частное положение относительно плоскостей проекций. В этом случае искомой линией пересечения является проецирующая прямая, проекция которой, вырожденная в точку, лежит на пересечении вырожденных в прямые проекциях плоскостей.

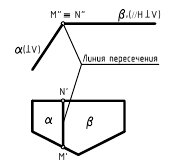
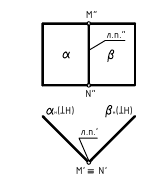
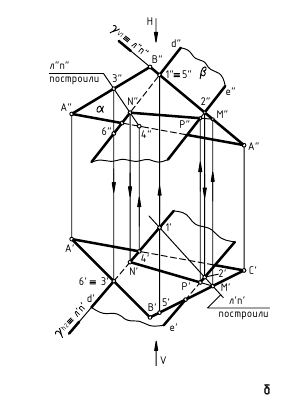
На рис. 4.2 изображены две пересекающиеся фронтально-проецирующие плоскости α и β, элементом пересечения которых является фронтально-проецирующая прямая m (соответственно, горизонтально-проецирующие плоскости пересекаются по горизонтально-проецирующей прямой). Фронтальная m(m») и вырожденная в точку проекция линии пересечения лежит на пересечении фронтальных, вырожденных в прямые, проекциях (следах) плоскостей, а горизонтальная m(m’) проекция линии пересечения – прямая, перпендикулярная оси x.

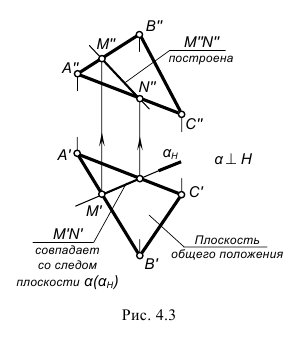
2-й случай – только одна из плоскостей занимает частное положение относительно плоскостей проекций. В этом случае одна из проекций искомой линии пересечения совпадает с вырожденной проекцией плоскости частного положения, а другую проекцию линии пересечения требуется построить.

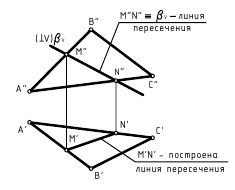
На рис. 4.3 изображены две пересекающиеся плоскости, из которых плоскость α, заданная своим горизонтальным следом α_h, является горизонтально-проецирующей, а другая плоскость, заданная треугольником ABC, – плоскость общего положения. Горизонтальная проекция MN(M’N’) искомой линии пересечения плоскостей в этом случае совпадает со следом αh плоскости α, а фронтальная проекция M»N» линии пересечения построена по принадлежности точек M и N сторонам треугольника ABC.

3-й случай – пересечение двух плоскостей общего положения, проекции которых в пределах чертежа накладываются, рассмотрим ниже.

. Если пересекаются три плоскости, то элементом их пересечения является точка!

Пересечение прямой с плоскостью

Общим элементом пересечения прямой с плоскостью является точка, принадлежащая и прямой и плоскости. Поскольку и прямая и плоскость могут занимать различные положения относительно плоскостей проекций, то при их пересечении также возможны три случая:

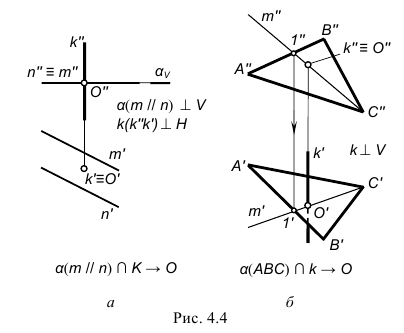
1-й случай – и прямая и плоскость занимают частное положение относительно плоскостей проекций. В этом случае проекции искомой точки пересечения определяются на характерных (вырожденных) проекциях прямой и плоскости.

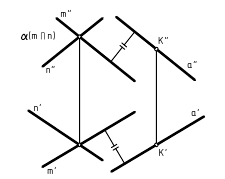
На рис. 4.4, а изображена горизонтальная плоскость уровня α(m//n), пересекающаяся с горизонтально-проецирующей прямой k(k»k’). Фронтальная проекция O(О») точки их пересечения совпадает с фронтальным следом плоскости α_V, а горизонтальная проекция O(O’) точки их пересечения совпадает с вырожденной в точку горизонтальной k(k’) проекцией прямой.

2-й случай – только один элемент (или прямая или плоскость) занимает частное положение относительно плоскостей проекций. В этом случае одна из проекций точки пересечения совпадает с характерной (вырожденной) проекцией элемента частного положения, а другую проекцию точки пересечения требуется построить.

На рис. 4.4, б изображены пересекающиеся фронтально-проецирующая прямая k(k»,k’) и плоскость общего положения, заданная треугольником АВС. В этом случае фронтальная проекция точки пересечения O(O») совпадает с вырожденной в точку проекцией прямой, а горизонтальная проекция O(O’) точки пересечения построена по принадлежности точки О плоскости АВС с помощью вспомогательной прямой m.

3-й случай – оба пересекающихся элемента занимают общее положение относительно плоскостей проекций, то есть пересекается плоскость общего положения с прямой общего положения. В этом самом сложном для решения случае для построения точки пересечения элементов следует применить вспомогательные построения, чтобы привести условие задачи к более легкому для решения 2-му случаю (см. рис. 4.4), то есть прямую общего положения заменить элементом частного положения, «заключив» эту прямую в плоскость частного положения (см. рис. 3.12 б, в).

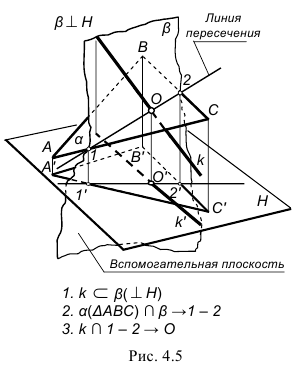
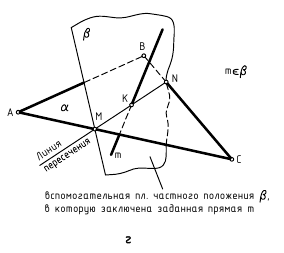
На рис. 4.5 показана наглядная картина этого действия. Прямая общего положения k пересекается с плоскостью общего положения α(ABC). Для решения задачи через прямую проведена некоторая вспомогательная плоскость β, то есть прямая «заключена» в плоскость β.

Определяется вспомогательная линия 1-2 пересечения двух плоскостей – заданной и вспомогательной. Искомая точка О лежит на пересечении заданной прямой k и вспомогательной линии пересечения 1-2.

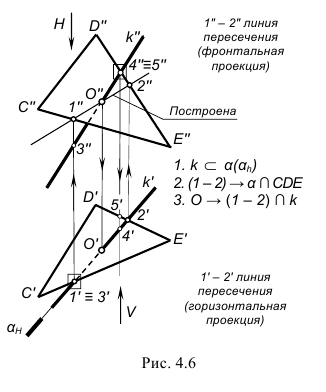
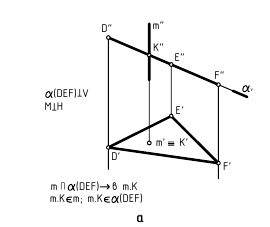
На рис. 4.6 показано построение на ч е р т е ж е точки пересечения O(O»,O’) плоскости общего положения, заданной треугольником CDE, c прямой общего положения k(k»,k’).

Для решения задачи в этом случае выполняется следующий графический алгоритм (графические действия):

1-е действие. Заключить прямую k во вспомогательную, например горизонтально-проецирующую плоскость α, задав ее горизонтальным следом α_H(k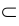α(α_H)).

2-е действие. Построить проекции вспомогательной линии пересечения 1-2(1″-2″,1′-2′) заданной плоскости CDE со вспомогательной плоскостью α(α∩β(∆CDE)):

– 1′-2′ совпадает со следом вспомогательной плоскости α(α_H);

– 1″-2″ строится по принадлежности точек 1 и 2 сторонам CE и DE плоскости β(∆CDE).

3-е действие. Определить проекции искомой точки пересечения O(O»,O’) заданных элементов: – фронтальная проекция O» определяется на пересечении фронтальной проекции заданной прямой k(k») и построенной фронтальной проекции 1″-2″ вспомогательной линии пересечения ((1″-2″)∩ k»);

– горизонтальная проекция O’ определяется на горизонтальной проекции k(k’) заданной прямой по линии связи (O’ 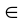k’).

4-е действие. Определить на проекциях относительную видимость прямой и плоскости по конкурирующим точкам 1-3 и 4-5.

На рис. 4.6 показано определение относительной видимости заданной прямой k и плоскости CDE с помощью конкурирующих точек, лежащих на скрещивающихся прямых. На горизонтальную проекцию наблюдатель смотрит сверху вниз по стрелке H. Чтобы определить, какой из элементов – прямая или плоскость – находится ближе к наблюдателю, рассмотрим проекции конкурирующих точек 1 и 3, лежащих на одном проецирующем луче, но на скрещивающихся прямых – точка 1 лежит на прямой СЕ, а точка 3 лежит на прямой k. Видно, что ближе к наблюдателю находится точка 1 на прямой СЕ, а точка 3 на прямой k расположена ниже. Это значит, что на горизонтальной проекции прямая k(k’) вниз от точки пересечения (О’) «уходит» плоскость CDE.

Аналогичными рассуждениями, рассмотрев конкурирующие точки 4 и 5 по стрелке V, определяем относительную видимость прямой и плоскости на фронтальной проекции чертежа – прямая k(k») находится над плоскостью CDE вверх от точки О(О»).

Пересечение двух плоскостей общего положения (3-й случай)

При задании пересекающихся плоскостей на чертеже возможны два варианта:

Для каждого варианта есть разные рациональные способы построения линии пересечения. Для варианта «а» рационально использовать две произвольные плоскости частного положения.

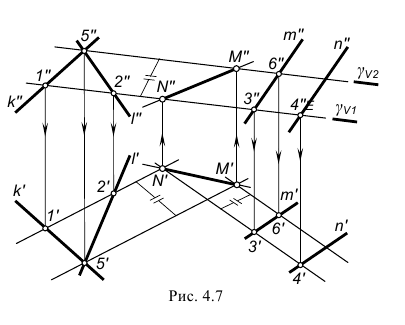
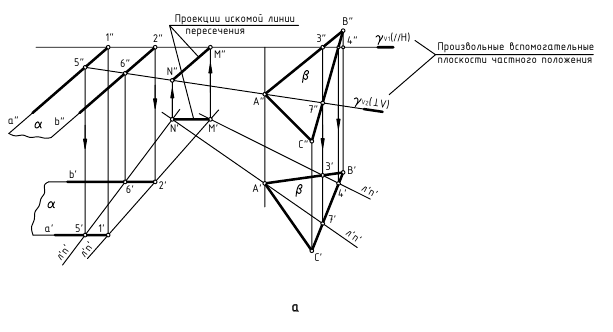
На рис. 4.7 показан пример построения линии пересечения плоскостей общего положения – α(k∩l) и β(m//n), проекции которых на чертеже не накладываются.

Линия пересечения заданных плоскостей построена по точкам N и M пересечения между собой вспомогательных линий пересечения этих плоскостей произвольными вспомогательными фронтально-проецирующими плоскостями γ₁ и γ₂ в соответствии со следующим графическим алгоритмом:

I. Построить точку N(N»,N’) пересечения заданных плоскостей α(k∩l) и β(m//n) вспомогательной горизонтальной плоскостью уровня γ₁:

1-е действие. Пересечь плоскости α(k∩l) и β(m//n) вспомогательной фронтально-проецирующей плоскостью уровня γ₁, обозначив ее фронтальный след γ_V1.

2-е действие. Построить проекции 1-2(1″-2″, 1′-2′) и 3-4(3″-4″, 3′-4′) вспомогательных линий пересечения заданных плоскостей α(k∩l) и β(m//n) вспомогательной плоскостью γ₁(γ_V1).

3-е действие. Определить проекции точки N(N»,N’) пересечения между собой вспомогательных линий 1-2(1″-2″, 1′-2′) и 3-4(3″-4″, 3′-4′).

II. Построить точку M(M»,M’) пересечения заданных плоскостей α(k∩l) и β(m//n) вспомогательной фронтально-проецирующей плоскостью γ₂(γ_V2), повторив графические действия 1, 2 и 3, и соединить прямой линией построенные точки N и M. Если при этом плоскость γ₂(γ_V2) задавать параллельно ранее заданной плоскости γ₁(γ_V1), то построения можно упростить и использовать не четыре, а только две точки 5 и 6, так как пересечение параллельными плоскостями будет давать параллельные вспомогательные линии.

Рассмотрим наиболее часто встречающийся в различных задачах вариант «б» – проекции плоскостей накладываются. Построение проекций линии пересечения сводится здесь к построению точек пересечения двух любых прямых одной плоскости с другой плоскостью, то есть к выполнению дважды графического алгоритма построения точки пересечения прямой общего положения с плоскостью общего положения, изложенного выше (см. рис. 4.6).

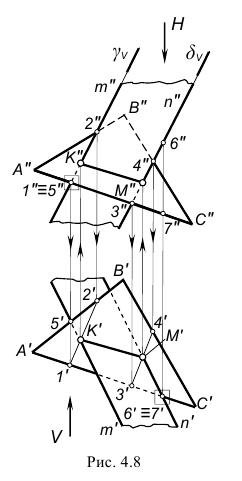
На рис. 4.8 показан пример построения линии пересечения плоскостей общего положения – α(ABC) и β(m//n), проекции которых на чертеже накладываются.

Линия пересечения построена по точкам K и M пересечения прямых m и n, которыми задана плоскость β(m//n), с плоскостью α(∆ABC), то есть дважды выполнен вышеприведенный графический алгоритм.

I. Построить точку K(K»,K’) пересечения прямой m с плоскостью α(∆ABC):

1-е действие. «Заключить» прямую m во вспомогательную фронтально-проецирующую плоскость γ и обозначить ее фронтальный след γ_V.

2-е действие. Построить проекции 1-2(1″-2″, 1′-2′) вспомогательной линии пересечения плоскостей – заданной α(∆ABC) со вспомогательной γ.

3-е действие. Определить проекции точки K(K»,K’) пересечения прямой m с плоскостью α.

II. Построить проекции точки M(M»,M’) пересечения прямой n с плоскостью α, повторив графические действия 1, 2 и 3 и соединить прямой линией построенные точки K и M.

4-е действие. Определить видимость плоскостей относительно построенной линии пересечения K–M, рассмотрев пары конкурирующих точек:

Структуризация материала четвертой лекции в рассмотренном объеме схематически представлена на рис. 4.9 (лист 1). На последующих листах 2–4 компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 4.10–4.12).

Взаимное положение двух плоскостей, прямой линии и плоскости:

Прямая, параллельная плоскости

Требуется: провести через т.К (К’,К») прямую, параллельную плоскости.

Решение: прямая а//α (m∩n), так как а∩m.

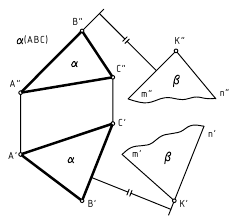
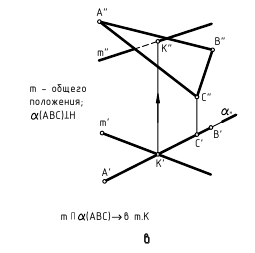
Требуется: провести через т.К (К’,К») плоскость β, параллельную заданной плоскости α(АВС).

Решение: плоскость β(m∩n) // α(АВС), так как m//АВ, а n//ВС.

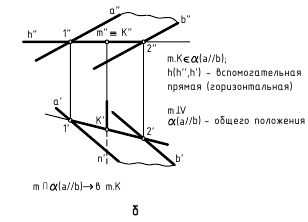
Требуется: провести через т.К (К’,К») плоскость β, параллельную заданной плоскости α(а//b).

Пересечение плоскостей частного положения

— знак «заключить»

Пересечение плоскости частного положения с плоскостью общего положения

Пересечение прямой частного положения с плоскостью частного положения

Пересечение прямой частного положения с плоскостью общего положения

Пересечение прямой общего положения с плоскостью частного положения

Пересечение прямой общего положения с плоскостью общего положения

Пересечение прямой общего положения с плоскостью общего положения

Пересечение плоскостей общего положения, проекции которых не накладываются (способ вспомогательных секущих плоскостей частного положения)

1. Пересечь заданные плоскости α(а//b) и β(АВС) вспомогательной горизонтальной плоскостью уровня γ₁(γ_V1)

2. Построить линии пересечения заданных плоскостей со вспомогательной:

3. Определить общую точку М(М’,М»), принадлежащую искомой линии пересечения М→1-2∩3-4

4. Повторить алгоритм и построить вторую точку N(N’,N»), принадлежащую искомой линии пересечения МN.

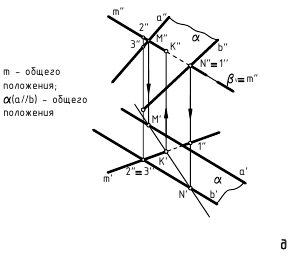
Пересечение плоскостей общего положения, проекции которых накладываются

Линия пересечения плоскостей строится по двум точкам пересечения прямых общего положения с плоскостью общего положения по алгоритму, приведённому для рис. 4.8.

1. Заключить прямую AB во вспомогательную фронтально-проецирующую плоскость γ₁(γ_V1).

2. Построить линию пересечения 1-2 заданной плоскости α(∆ABC) со вспомогательной плоскостью γ₁.

3. Определить первую общую точку M(M’,M») линии пересечения заданных плоскостей.

4. Повторить алгоритм, заключив прямую α заданной плоскости β (d//e) во вспомогательную горизонтально-проецирующую плоскость γ₂(γ_h2) и определить вторую общую точку N(N»,N’).

6. Определить относительную видимость плоскостей по конкурирующим точкам: 1 и 5, 6 и 3.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник