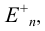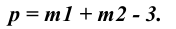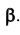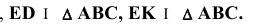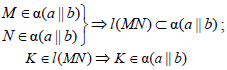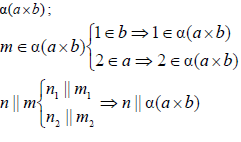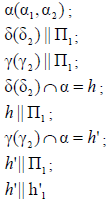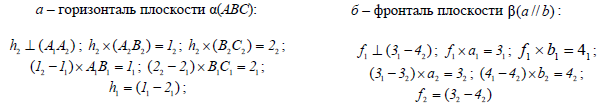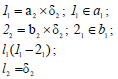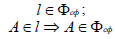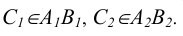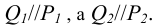Как построить плоскость параллельную данной

Позиционные задачи в начертательной геометрии с примерами

Содержание:

Позиционными задачами называются задачи на построение элементов, общих для взаимодействующих объектов, и задачи на взаимное положение геометрических объектов. Первая группа задач включает задачи на принадлежность и задачи на пересечение. Ко второй группе задач относятся задачи на параллельность геометрических объектов.

Задачи на перпендикулярность объектов относят к метрическим задачам, которые будут рассмотрены в следующем разделе. Позиционные задачи, в которых участвуют поверхности, будут рассмотрены в главе «Поверхности».

Классификация позиционных задач, относящихся к элементарным геометрическим объектам (точка, прямая, плоскость), представлена на рисунке 4.1.

Позиционные задачи

Задачи, связанные с определением взаимного расположения геометрических объектов в пространстве, традиционно называют позиционными.

Поскольку Начертательная геометрия изучает объекты расширенного Евклидова пространства

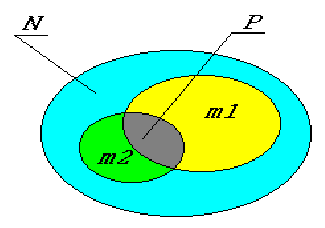
В линейной алгебре утверждается, что для всех объектов пространства справедливо выражение (в соответствии с рисунком 4.1)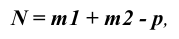

где N— размерность рассматриваемого пространства,

— размерность объектов этого пространства, р — размерность пересечения этих объектов.

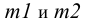
Очевидно, все позиционные задачи, с точки зрения линейной алгебры, можно свести к определению вида и размерности пересечения.

Полагая, что рассматриваемое
пространство трехмерно, при вычислении размерности пересечения исходное выражение примет вид

Задачи на принадлежность

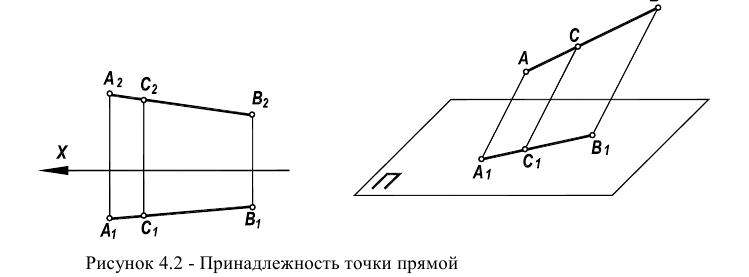
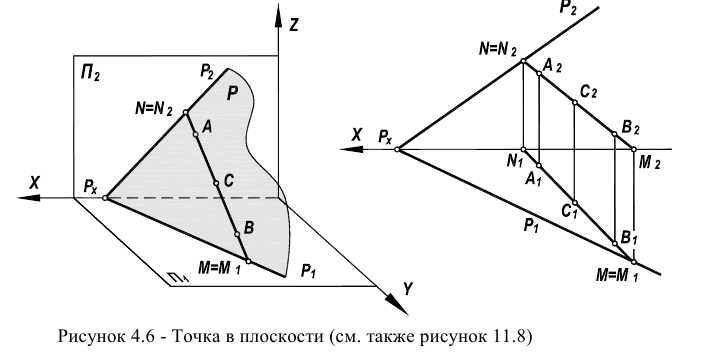
Точка принадлежит плоскости, если она принадлежит прямой, находящейся в этой плоскости (рисунок 4.2а). Прямая принадлежит плоскости, если она проходит через две точки, принадлежащих плоскости. Поэтому для того, чтобы указать в плоскости какую-либо точку, необходимо сначала указать в плоскости прямую, а затем на этой прямой указать положение точки.

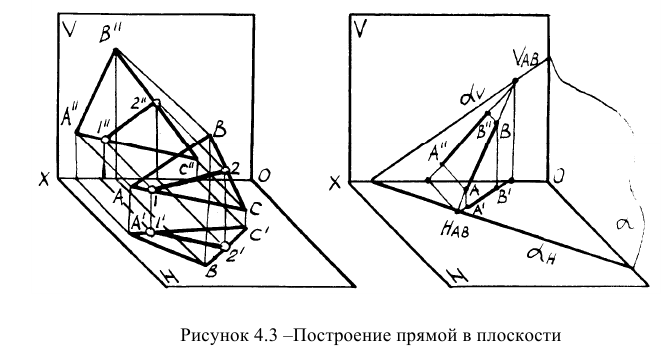
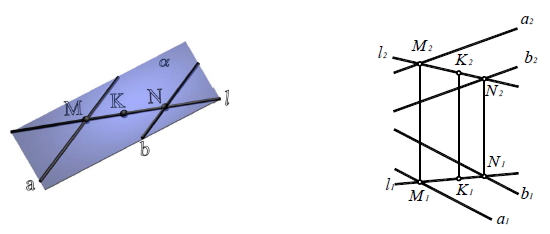
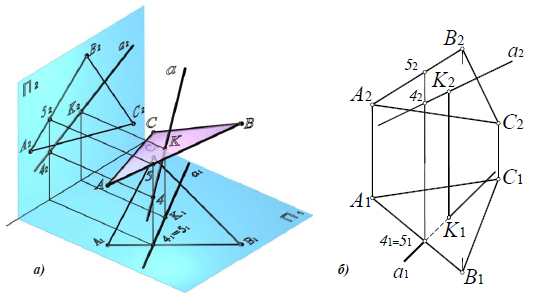
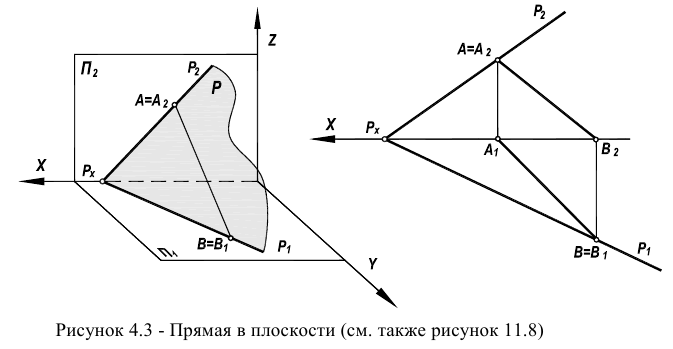
На рисунках 4.3 показано построение прямой в плоскостях, заданных треугольником и следами. Если плоскость задана треугольником, то целесообразно упомянутые точки взять на сторонах треугольника. Если плоскость задана следами, то в качестве двух точек целесообразно взять следы прямой. Это основано на следующем свойстве: если плоскость задана следами и в ней находится прямая, то следы прямой лежат на одноименных следах плоскости.

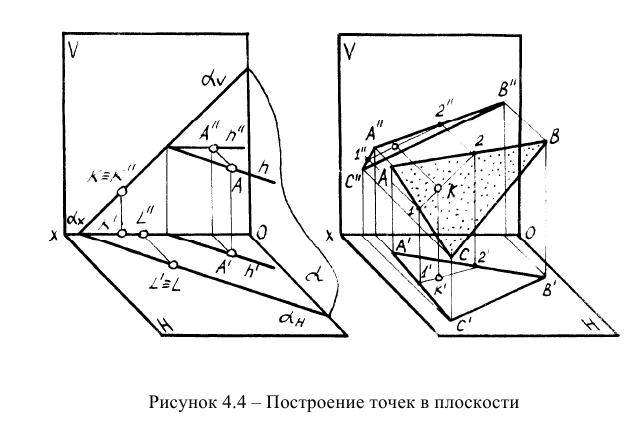
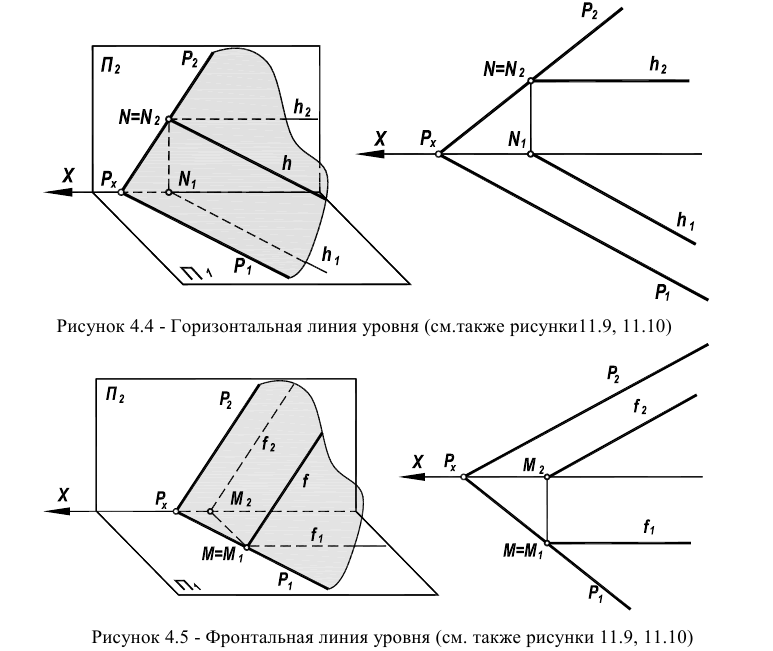
На рисунке 4.4 представлено построение точек в плоскости, заданной следами и точки в плоскости, заданной треугольником. В первом случае точка А построена с помощью горизонтали. На этом же рисунке показано построение точек (К и L), находящихся на следах плоскости. Во втором случае точка К построена с помощью прямой 1-2.

С рассматриваемым вопросом тесно связан вопрос о проведении плоскости частного положения (например, проецирующих плоскостей) через прямую.

Если прямая принадлежит плоскости частного положения и плоскость задается следами, то одна из проекций прямой будет совпадать с собирательным следом плоскости в соответствие с рисунком 4.5.

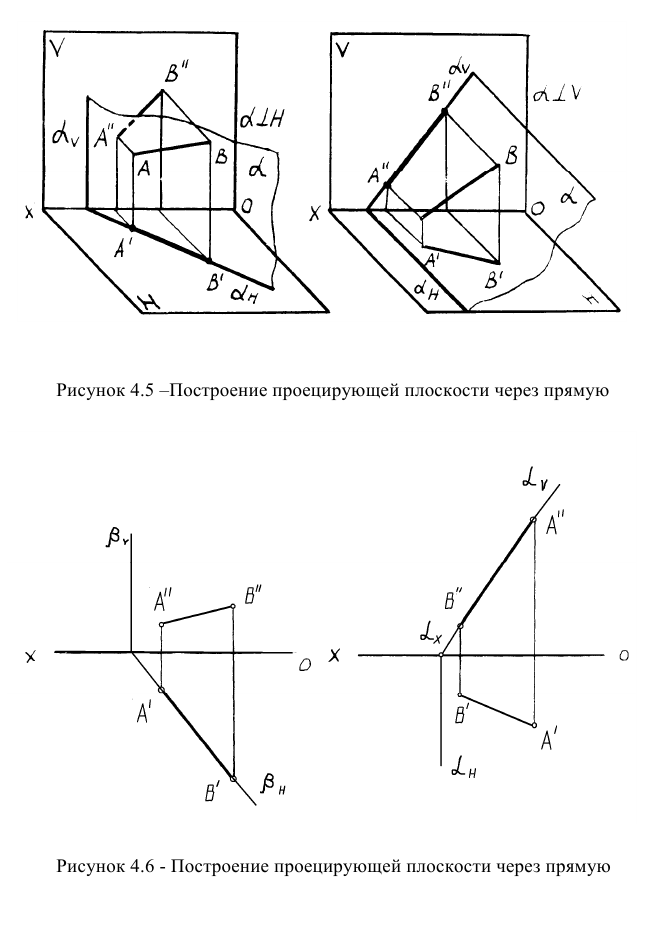
На рисунке 4.6 в эпюрной форме показано проведение через прямую фронтально проецирующей плоскости а и горизонтально проецирующей плоскости

Задачи на пересечение

Задача на пересечение двух прямых рассмотрена ранее в разделе «Пересекающиеся прямые».

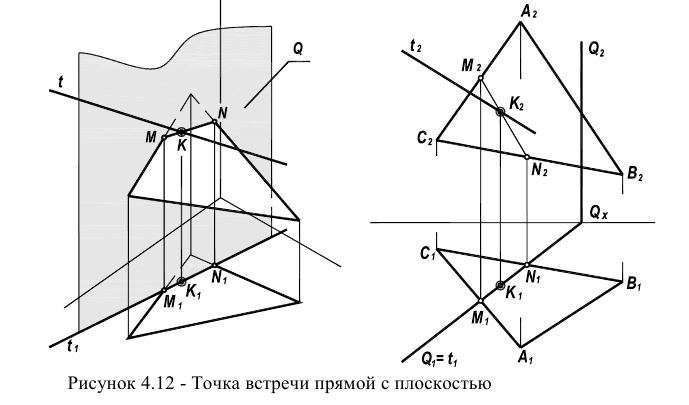
Наиболее важной позиционной задачей является задача о пересечении прямой с плоскостью. При решении задачи могут встретиться следующие случаи пересечения:

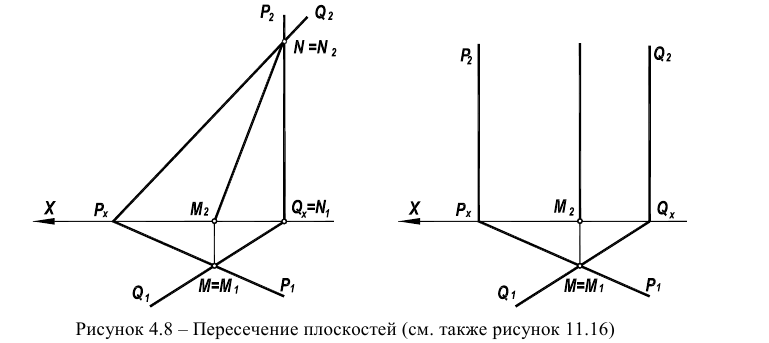
Для решения задачи о пересечении прямой с плоскостью в общем положении разработана следующая методика (рисунок 4.8а):

На рисунке 4.86 дана пространственная схема решения задачи, в которой прямая пересекается с плоскостью, заданной следами. В качестве вспомогательной плоскости взята горизонтально-проецирующая плоскость.

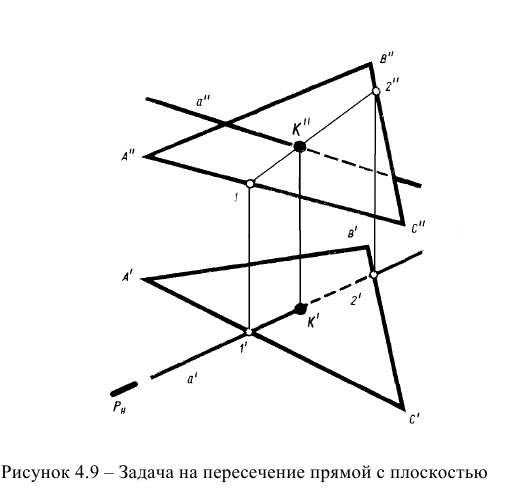
На рисунке 4.9 дано решение задачи на пересечение прямой общего положения с плоскостью общего положения, заданной треугольником. В качестве вспомогательной плоскости использована горизонтально-проецирующая плоскость.

Видимость проекций определена методом конкурирующих точек (прямых).

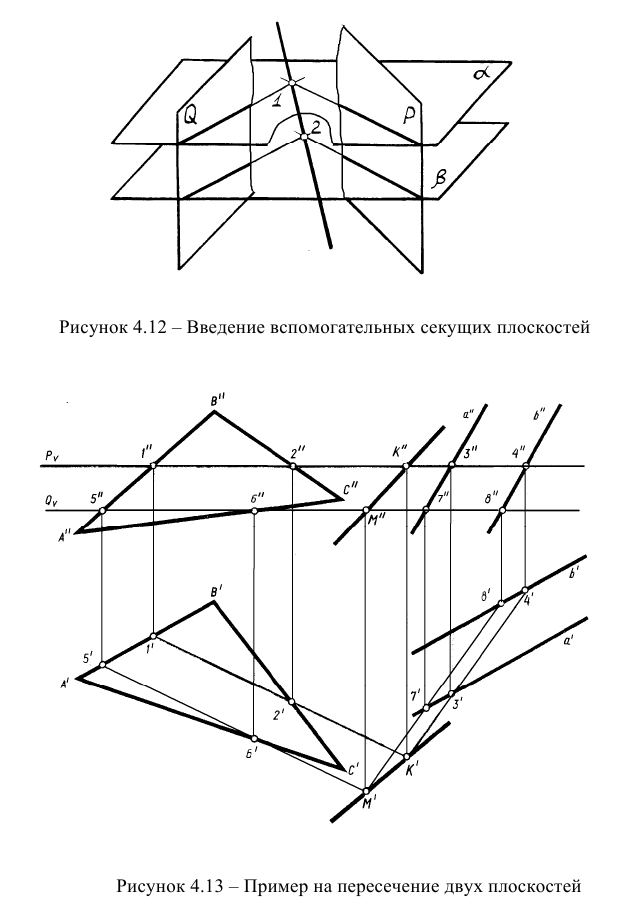
Сущность метода заключается в том, что заданные плоскости Q и Р дважды пересекают вспомогательными плоскостями а и 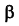(например, горизонтальными). Находят линии их пересечения с заданными плоскостями, далее находят точки 1 и 2 пересечения найденных линий и соединяют полученные точки прямой линией, которая является линией пересечения заданных плоскостей.

Если пересекающиеся плоскости являются плоскостями частного положения, или если одна из пересекающихся плоскостей является плоскостью частного положения, то задача упрощается. На рисунке 4.14 представлены примеры решения задач на пересечение упомянутых плоскостей. И более трудоемкой задачей является задача на пересечение двух плоскостей общего положения, заданных плоскими фигурами, например, треугольниками, многоугольниками и т.д.

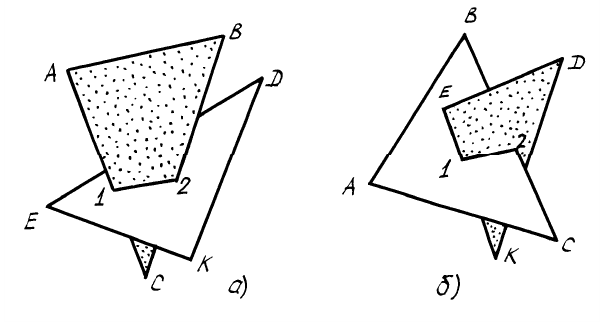
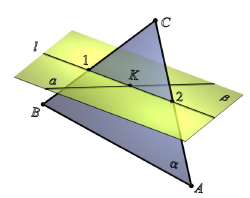
При пересечении плоских фигур возможны два случая пересечения (рисунок 4.15): полное пересечение (а) и неполное пересечение (б).

В обоих случаях линия пересечения треугольников определяется двумя точками 1 и 2, каждая из которых определяется как точка пересечения стороны одного треугольника с плоскостью другого. Отсюда следует вывод: для того, чтобы построить линию пересечения

треугольников, необходимо дважды решить задачу о пересечении стороны одного треугольника с плоскостью другого треугольника (типовая задача о пересечении прямой с плоскостью). При этом пару пересекающихся объектов можно подбирать произвольно. В любом случае линия пересечения будет построена.

Задачи на параллельность

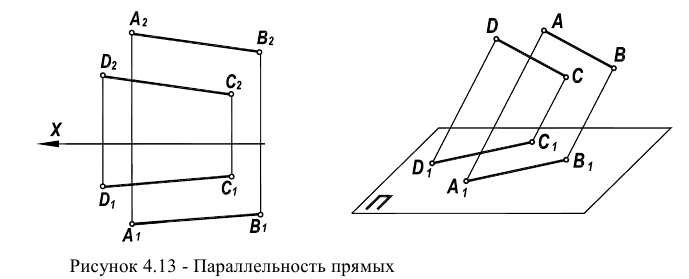
Задача на параллельность двух прямых была рассмотрена ранее в разделе «Параллельные прямые».

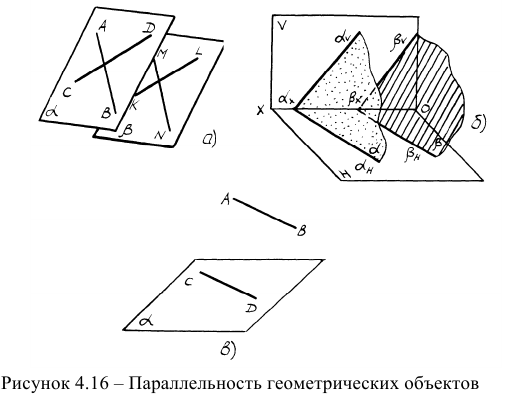
Задачи на параллельность плоскостей основываются на положениях элементарной геометрии. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости взаимно параллельны двум пересекающимся прямым другой плоскости (рисунок 4.16а).

Если две параллельные плоскости заданы следами, то одноименные следы таких плоскостей параллельны друг другу (рисунок 4.166).

Прямая будет параллельна плоскости в том случае, если она параллельна любой прямой, находящейся в этой плоскости.

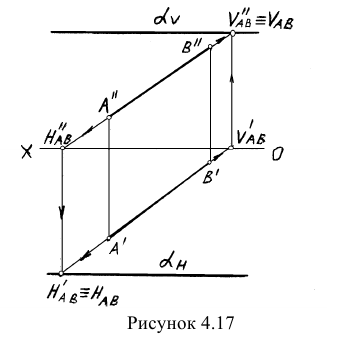
Пример: Через прямую АВ провести профильно-проецирующую плоскость (рисунок 4.17).

Решение: Как было показано ранее горизонтальный и фронтальный следы профильно-проецирующей плоскости располагаются параллельно оси ОХ. Было также показано, что если прямая принадлежит плоскости, заданной следами, то следы прямой находятся на одноименных следах плоскости. Сказанное позволяет разработать план решения задачи:

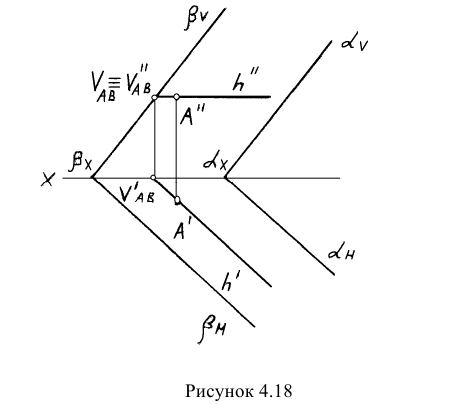
Пример: Через точку провести плоскость, параллельную заданной (рисунок 4.18).

Решение: Плоскость задана следами. Искомую плоскость целесообразно тоже задать следами. Чтобы обеспечить параллельность плоскостей, необходимо следы искомой плоскости провести параллельно одноименным следам заданной плоскости.

Для того чтобы искомая плоскость проходила через заданную точку, необходимо через точку провести прямую (например, горизонталь), которая принадлежала бы искомой плоскости. Исходя из изложенного, определяется следующий план решения задачи:

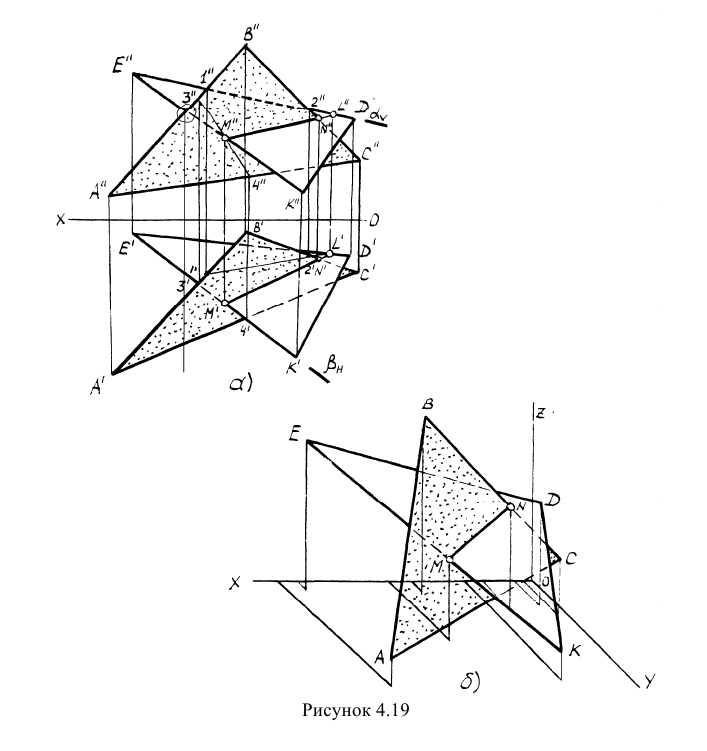
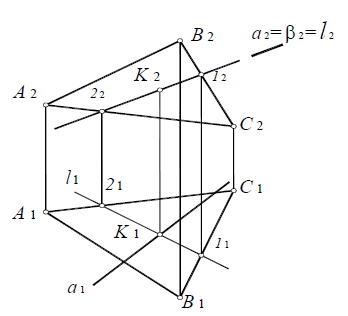
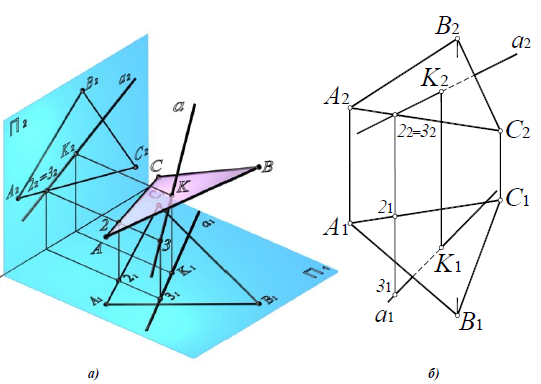
Пример: Построить линию пересечения треугольников АВС и EDK, определить видимость проекций (рисунок 4.19).

Построить линию пересечения треугольников АВС и EDK, определить видимость проекций (рисунок 4.19).

Решение: Предварительно намечаем две произвольные задачи на пересечение стороны одного треугольника с плоскостью другого (произвольно). Например,

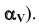
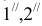
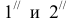
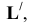
Решаем первую задачу. Через ED проводим вспомогательную фронтально-проецирующую плоскость а (след плоскости — Она пересекает треугольник АВС в двух точках на сторонах АВ и ВС. Находим горизонтальные проекции этих точек и соединяем их. Линия 1-2 является линией пересечения вспомогательной плоскости с плоскостью треугольника АВС. Ищем точку пересечения линии 1-2 с прямой ED. Это точка , которая лежит вне треугольника АВС, но является точкой линии пересечения треугольников.

Аналогично решаем вторую задачу. В качестве вспомогательной плоскости берем горизонтально-проецирующую плоскость 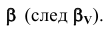В результате решения задачи получаем точку М.

Далее соединяем полученные точки L и М. Однако не вся эта линия будет являться линией пересечения треугольников, а лишь участок MN, который принадлежит обоим треугольникам. Таким образом, в результате решения двух произвольно выбранных задач получили линию MN пересечения заданных треугольников.

Определяем видимость проекций треугольников. При определении видимости проекций методом конкурирующих точек (прямых) необходимо учитывать следующие особенности:

Учет перечисленных особенностей позволяет определить видимость проекций треугольников по анализу одного конкурирующего места на каждой проекции, что значительно ускоряет решение задачи.

Отметим на фронтальной проекции любое конкурирующее место из шести (отмечено кружочком). Проведем через него линию связи и вдоль линии связи сравним ординаты конкурирующих прямых ЕК и АВ. Наибольшую ординату имеет прямая АВ. Она и будет видна на рассматриваемой фронтальной проекции. Видимость остальных сторон треугольников определяется с учетом особенностей, отмеченных выше.

На горизонтальной проекции отметим конкурирующее место, в котором конкурируют прямые АВ и ED. Аналогично описанному определяем, что на горизонтальной проекции будет видна прямая АВ, так как у ней наибольшая аппликата. Видимость остальных сторон треугольников определим аналогично рассмотренному выше.

Для усиления эффекта видимости треугольников на проекциях целесообразно один их треугольников заштриховать с учетом видимости или раскрасить оба треугольника.

Относительное положение прямой и плоскости

Прямая по отношению к плоскости может занимать три различных
положения:

Принадлежность точки и прямой линии плоскости

Прямая линия принадлежит плоскости, если две точки этой прямой принадлежат плоскости (рис. 8.2).

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости (см. рис. 8.2).

Рис. 8.2. Принадлежность точки и прямой линии плоскости:

Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости (рис. 8.3).

Рис. 8.3. Параллельность прямой и плоскости:

Линии уровня плоскости

Прямые, лежащие в данной плоскости и параллельные одной из плоскостей проекций, называются линиями уровня плоскости.

Прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций П1, называется горизонталью плоскости (рис. 8.4). Все горизонтали плоскости параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и горизонтальной плоскости уровня.

Рис. 8.4. Горизонтали плоскости:

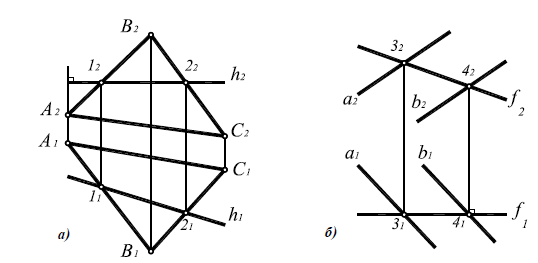
Рассмотрим построение горизонтали плоскости общего положения α(ABC) (рис. 8.5,а).

Рис. 8.5. Линии уровня плоскости:

Фронталь плоскости β( a||b )строится аналогично, но построение фронтали начинается с построения ее горизонтальной проекции (рис. 8.5,б). Все фронтали плоскости также параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и фронтальной плоскости уровня.

Пересечение прямой общего положения и плоскости частного положения

Рассмотрим построение точки пересечения K фронтально-проецирующей плоскости γ(γ₂)П₂ и прямой a(α₁,a₂) общего положения (рис. 8.6).

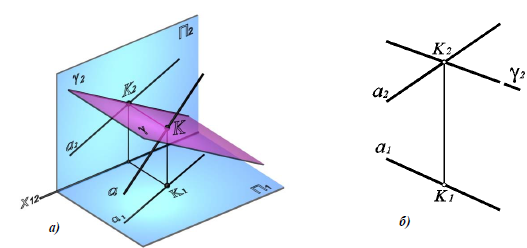
Пересечение двух плоскостей частного положения

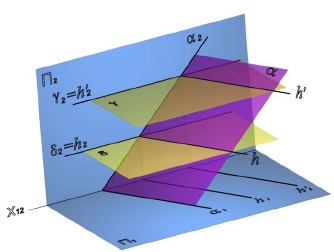
Линией пересечения двух фронтально-проецирующих плоскостей δ(δ₂) и σ(σ₂) является фронтально-проецирующая прямая l (рис. 8.7).

линии пересечения двух фронтально-проецирующих плоскостей δ(δ₂)и σ(σ₂)определяется как точка пересечения фронтальных следов плоскостей δ₂ и σ₂: l₂=δ₂×σ₂, а горизонтальная проекция строится по линии связи, перпендикулярно направлению оси x₁₂.

Пересечение плоскости общего положения и плоскости частного положения

Линией пересечения двух плоскостей (рис. 8.8) является прямая, для построения которой достаточно определить две точки, принадлежащие обеим плоскостям одновременно.

Рассмотрим построение линии пересечения l плоскости общего положения α(a×b) и фронтально-проецирующей плоскости δ(δ₂)(рис. 8.8, б). Линия, по которой пересекаются две плоскости, принадлежит обеим плоскостям одновременно, следовательно, для ее построения достаточно определить две точки, общие для пересекающихся плоскостей, или одну точку и направление линии пересечения.

В данном случае, достаточно определить точки пересечения прямых а и b с плоскостью δ(δ₂). Они однозначно определят линию пересечения l.

Пересечение прямой общего положения и плоскости общего положения. Первая позиционная задача

Задача об определении точки пересечения прямой общего положения с плоскостью общего положения называется первой позиционной задачей. На рис. 8.9 представлено наглядное изображение решения первой позиционной задачи.

Рис. 8.9. Пересечение прямой общего положения и плоскости общего положения

Определить: K=a×α(ABC).

Решение:

1. Прямую заключить во вспомогательную плоскость частного положения: αeβ.

2. Определить линию l как линию пересечения вспомогательной и заданной плоскостей l=α (ABC) β.

3. Определить взаимное положение заданной прямой a и полученной прямой l.

Поскольку прямые a и l лежат в одной плоскости, они могут пересекаться или быть параллельными. Точка пересечения K=a×l и является искомой точкой пересечения прямой а с плоскостью α(ABC). Если прямые a и l параллельны, то прямая а параллельна плоскости α(ABC).

Определение точки пересечения прямой a(a1,a2) и плоскости α(ABC) на комплексном чертеже:

2. Определить линию пересечения l(1-2) вспомогательной плоскости β(β₂) и заданной плоскости α(ABC):
l = α(ABC) β(β₂); 1₂=β₂; l₁=( 1₁-2₂).

Рис. 8.10. Пересечение прямой a(a₁,a₂ )и плоскости α( ABC)

3. Определить взаимное положение заданной прямой a и полученной прямой l. В данном случае, прямые а и lпересекаются в точке K, которая и является искомой точкой пересечения прямой a(a1,a2) и плоскости α(ABC):
1₁×a ₁=K₁; K₂∈a₂; K= a(a_1,a₂)×α(ABC).

Видимость прямой а по отношению к плоскости α(ABC) на фронтальной плоскости проекций (рис. 8.12) определяется с помощью конкурирующих точек 2на прямой (AC) и 3-на прямой а. Глубина точки 3 больше, следовательно, видима будет прямая а.

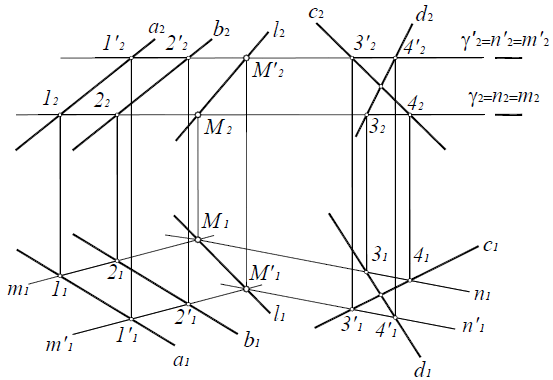
Пересечение двух плоскостей общего положения. Вторая основная позиционная задача

Рис. 8.13. Пересечение двух плоскостей общего положения

Алгоритм решения второй позиционной задачи состоит в следующем:

1. Заданные плоскости α(a||b) и β(c×d) пересечь вспомогательной плоскостью частного положения γ.

3. Определить точку M пересечения линий m и n. Точка M принадлежит прямой m, а, следовательно, и плоскости α (a||b). Точка M принадлежит прямой n, следовательно, и плоскости β(c×d). Таким образом, точка M принадлежит обеим плоскостям, то есть является одной из точек линии пересечения.

4. Вторую точку линии пересечения определяют аналогично, рассекая плоскости α(a||b) и β(c×d) вспомогательной плоскостью частного положения γ’.

Определение линии пересечения двух плоскостей общего положения α(a||b) и β(c×d) на комплексном чертеже:

1. Пересечь данные плоскости вспомогательной фронтально-проецирующей плоскостью γ(γ₂)П₂ (рис. 8.14).

2. Определить линии пересечения вспомогательной плоскости с каждой из заданных плоскостей:
m =γ(γ₂)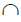α(a||b); m₂=γ₂;
n =γ(γ₂)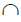β(c×d); n₂=γ₂;

3. Определить точку пересечения прямых n и m:M=n× m.

4. Точка M ⊂ m M ⊂ a(a || b); M ⊂ nM ⊂ β(c ×d) таким образом, точка M является одной из точек искомой линии пересечения плоскостей.

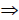
5. Точка M’ определяется аналогично, вспомогательной плоскости γ / (γ / ₂).

Рис. 8.14. Вторая позиционная задача

Сечение поверхности плоскостью

Если проекция линии пересечения этими точками не определяется полностью, то строят дополнительные, промежуточные между опорными, точки. При построении сечений секущая плоскость обычно считается прозрачной и определяется только видимость поверхности и линии сечения.

Точка на поверхности

Рис. 8.15. Точка на поверхности сферы:

Любая плоскость рассекает поверхность сферы по окружности (рис. 8.15), но без искажения на соответствующую плоскость проекций проецируются только окружности, лежащие в плоскостях уровня. Таким образом, для построения точки на поверхности сферы в качестве вспомогательных плоскостей используются только плоскости уровня.

На поверхности конуса можно получить как окружности, так и прямые линии.
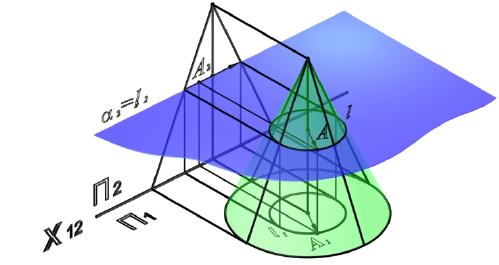
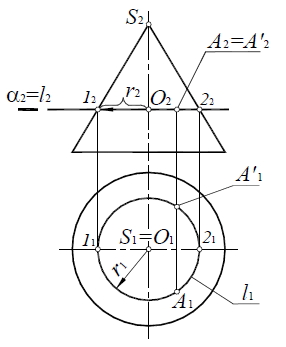
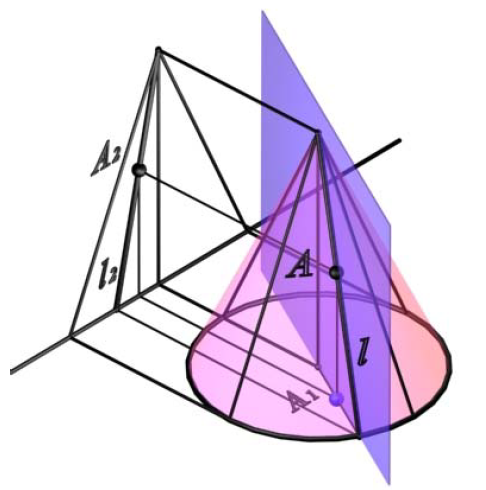
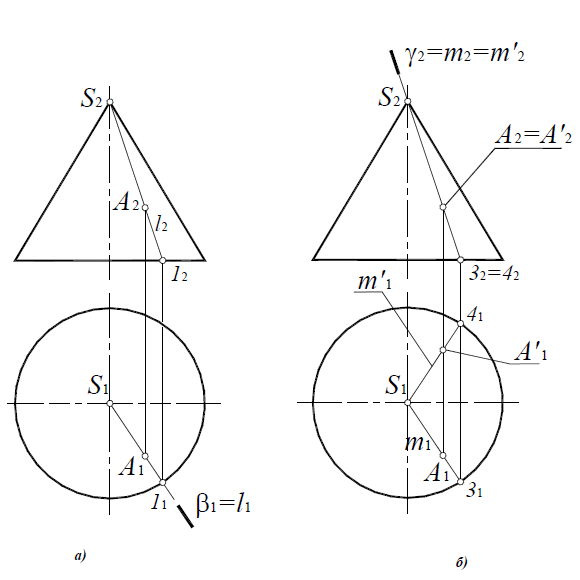
Для построения горизонтальной проекции точки A на поверхности конуса (рис. 8.16, 8.17), конус рассекается горизонтальной плоскостью уровня α(α₂), проходящей через точку A.

Рис. 8.16. Точка на поверхности конуса

Рис. 8.17. Построение точки на поверхности конуса

Поскольку любая плоскость, проходящая через вершину конуса, рассекает его по двум пересекающимся прямым, вспомогательную плоскость можно задать точкой A и осью вращения конуса (рис. 8.18).

Рис. 8.18. Точка на поверхности конуса

Если необходимо определить фронтальную проекцию точки A, принадлежащей поверхности конуса (рис. 8.19,а), конус рассекается вспомогательной горизонтально-проецирующей плоскостью β(A, i), проходящей через ось вращения конуса и искомую точку. Плоскость β(A, i) пересекает основание конуса в точке 1. Вершина конуса S и точка 1 определят образующую конуса l, проходящую через точку A:

.

Сечение поверхности вращения плоскостью частного положения

Точки 4 и 5 пересечения полученных линий принадлежат секущей плоскости μ(μ 2 ) и линии l поверхности тора, то есть принадлежат плоскости и поверхности одновременно, а следовательно, являются точками искомой линии пересечения m.

Точки 6, 7, 8 и 9 определяются аналогично. Полученные точки соединяют плавной лекальной кривой и определяют видимость линии пересечения m относительно поверхности.

Рис. 8.20. Сечение поверхности вращения плоскостью частного положения

При построении сечений поверхности плоскостью общего положения выполняют такое преобразование комплексного чертежа, при котором плоскость займет частное положение.

Цилиндрические сечения

В сечении цилиндрической поверхности вращения плоскостью могут быть получены следующие линии:

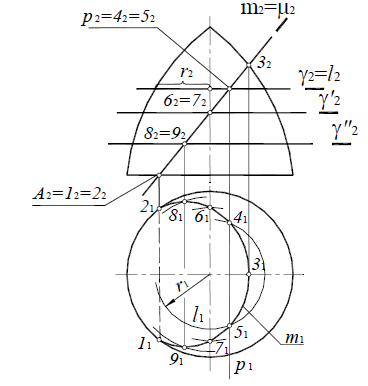
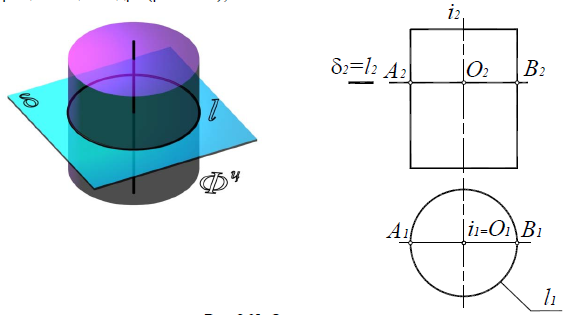
Окружность, если секущая плоскость δ(δ₂) перпендикулярна оси вращения цилиндра (рис. 8.21);

Рис. 8.21. Окружность

Эллипс, если секущая плоскость α(α₂) наклонена под произвольным углом к оси цилиндра (рис. 8.22);

Рис. 8.22. Эллипс

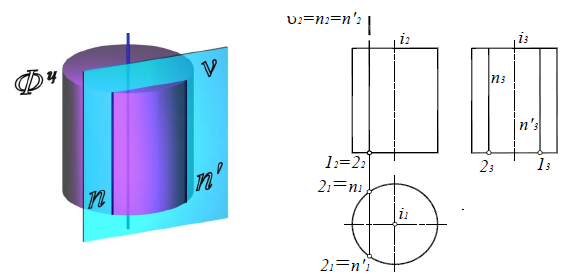
Две параллельные прямые (образующие), если секущая плоскость ν(ν2)
параллельна оси цилиндра (рис. 8.23)

Рис. 8.23. Параллельные прямые

На плоскость, перпендикулярную оси вращения поверхности, окружность и эллипс на поверхности цилиндра проецируются в окружность, совпадающую с проекцией всей поверхности.

Конические сечения

Кривые линии, которые получаются в сечении прямого кругового конуса плоскостью, называются коническими сечениями. В зависимости от положения секущей плоскости по отношению к конической поверхности образуются
следующие линии:

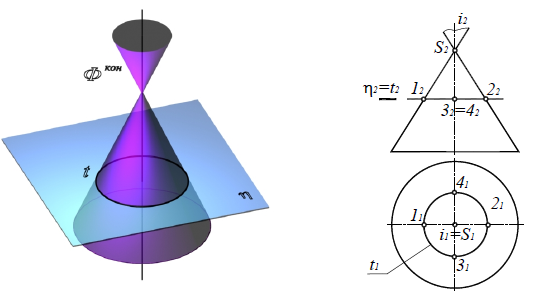
Окружность, если секущая плоскость η(η₂) перпендикулярна оси вращения конуса i (рис. 8.24).

Рис. 8.24. Окружность

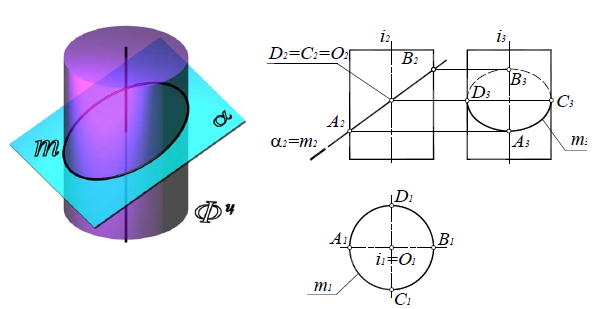
Две пересекающиеся прямые, если секущая плоскость β(β₂) проходит через вершину поверхности конуса (рис. 8.25).

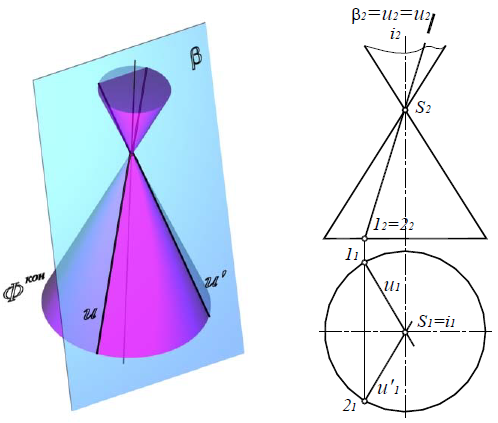
Рис. 8.25. Пересекающиеся прямые

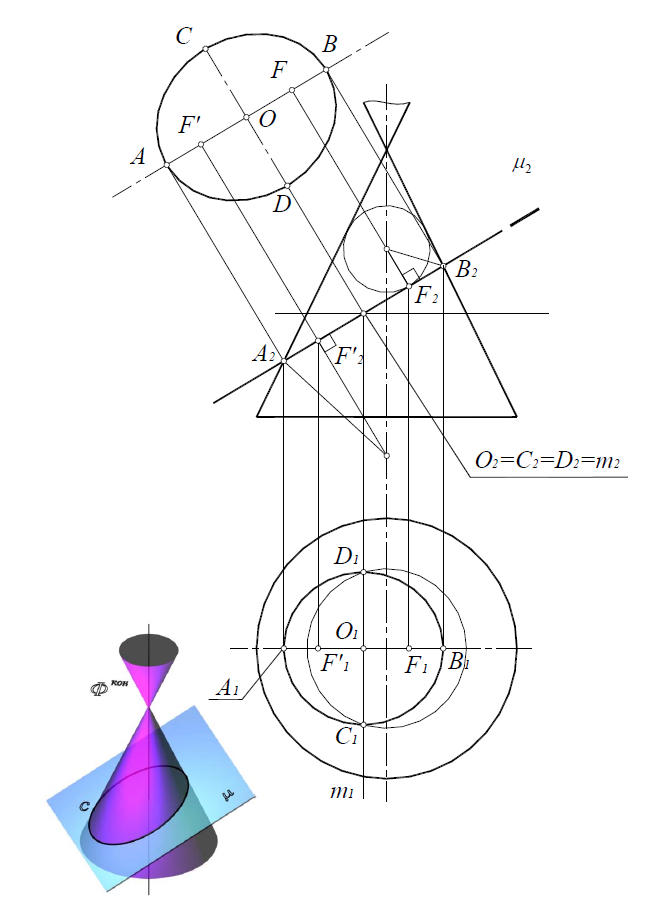
Эллипс (рис. 8.26), если секущая плоскость μ(μ₂) пересекает все образующие, расположенные по одну сторону от вершины конуса.

Для построения фокуса проводят биссектрису угла S₂B₂A₂, между образующей конуса и следом секущей плоскости μ₂ до пересечения с осью конуса. Из полученной точки опускают перпендикуляр на след плоскости μ2. Эта точка F и является фокусом. Из точки A₂ откладывают расстояние AF’=FB.

Свойство эллипса: сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равна большой оси эллипса АВ=FP+F’P.

Рис. 8.26. Эллипс

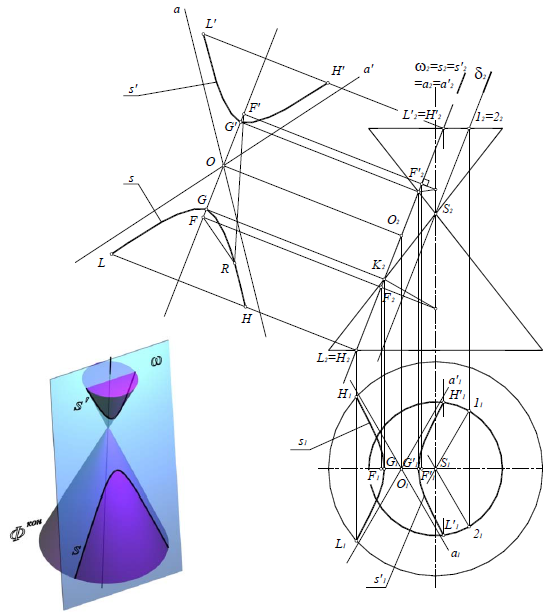
Парабола (рис. 8.27), если секущая плоскость λ(λ₂) параллельна одной из образующих поверхности конуса.

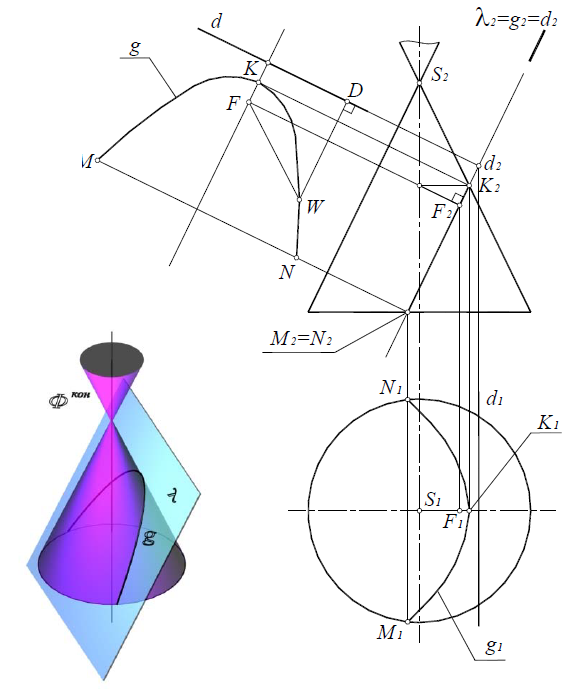
Рис. 8.27. Парабола

Свойство параболы: расстояние от любой точки параболы до ее фокуса равно расстоянию от этой точки до директрисы WD=WF.

Гипербола (рис. 8.28), если секущая плоскость ω(ω₂) пересекает обе половины поверхности конуса.

Рис. 8.28. Гипербола

Свойство гиперболы: разность расстояний от любой точки гиперболы до ее фокусов есть величина постоянная, равная расстоянию между вершинами гиперболы RF-RF’=GG’.

Пересечение прямой с поверхностью

Прямая по отношению к поверхности может занимать следующие положения:

Алгоритм решения задач об определении взаимного положения поверхности и прямой аналогичен решению первой позиционной задачи (рис. 8.29):

Рис. 8.29. Пересечение прямой с поверхностью

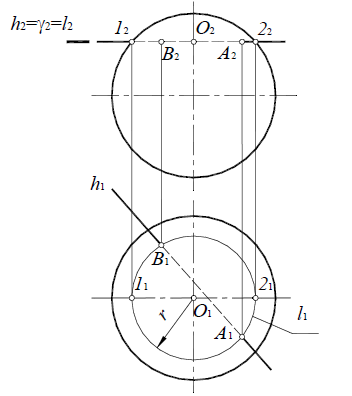
Для построения точки пересечения поверхности сферы с горизонталью (рис. 8.30), горизонталь заключают во вспомогательную горизонтальную плоскость уровня γ(γ₂).

Сечение сферы горизонтальной плоскостью уровня представляет собой окружность l с центром в точке O₂ и радиусом r=O₂l₂, которая проецируется на П₁ без искажения. Затем определяются точки пересечения окружности l₁ и заданной горизонтали h₁ :
h ₁×1₁=A₁, B₁; A₂, B₂∈h₂.

Рис. 8.30. Пересечение прямой с поверхностью сферы

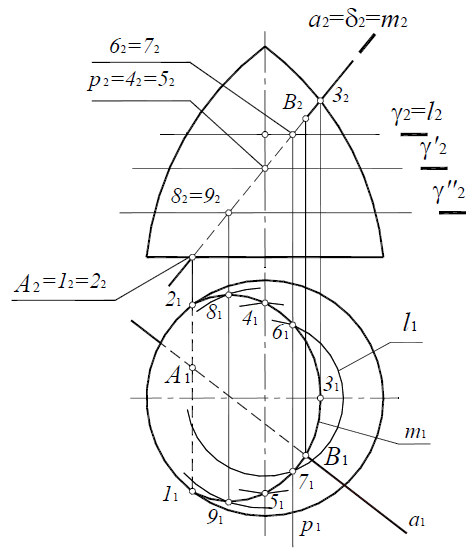
Для построения точки пересечения поверхности закрытого тора с прямой общего положения (рис. 8.31), прямую заключают во вспомогательную фронтально-проецирующую плоскость δ(δ₂). Далее строится сечение тора плоскостью δ(δ2):

Точки 4 и 5 также опорные (лежат на образующих, проекции которых совпадают с осью тора). Точки 4 и 5 определяются как точки на поверхности тора с помощью вспомогательной плоскости γ’.

Промежуточные точки 6,7,8,9 определяются аналогично.

Рис. 8.31. Пересечение прямой общего положения с поверхностью тора

3. Определить видимость прямой относительно поверхности тора.

Принадлежность точки и прямой

Вопрос о принадлежности точки прямой решается на основе свойств (особенностей) метода проецирования. Точка С лежит на прямой АВ, если ее проекции, в соответствии с рисунком 4.2, лежат на одноименных проекциях Прямой

В геометрии принято считать, что прямая принадлежит плоскости, если две ее точки (действительные или несобственные) принадлежат этой плоскости (рисунки 4.3, 11.8)

При условии, что одна из точек плоскости, через которые проходит прямая, лежит на следе и является несобственной (в соответствии с рисунками 4.4 и 4.5), прямая общего положения переходит в прямую частного положения (линию уровня).

В плоскости различают горизонтальную линию уровня h (рисунки 4.4, 11.9) и фронтальную линию уровня 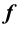(рисунки 4.5, 11.9).

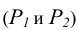
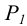
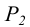
В силу специального расположения следов плоскости они (следы) являются линиями уровня. След является горизонталью, а — фронталью этой плоскости.

Фронтали и горизонтали плоскости получили название главных линии плоскости.

Вопрос о принадлежности точки плоскости можно свести к предыдущей задаче. Достаточно добиться того, чтобы точка лежала на одной из прямых плоскости (рисунки 4.6, 11.8)

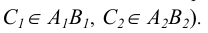
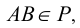
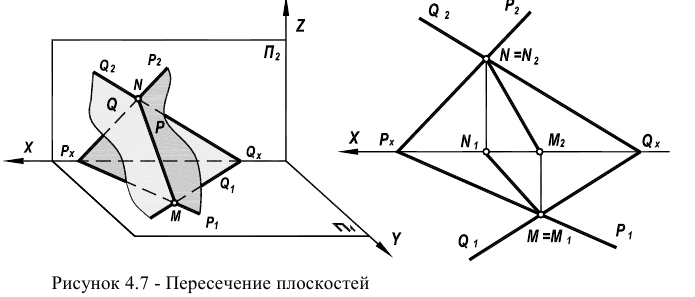
Точка С лежит на прямой АВ (ее проекции, в соответствии с рисунком 4.2, лежат на одноименных проекциях прямой Прямая т.к. две ее точки принадлежат плоскости Последнее утверждение очевидно вследствие того, что эти точки лежат на следах плоскости. Следовательно, можно утверждать что (рисунок 4.6).

Пересечение плоскостей

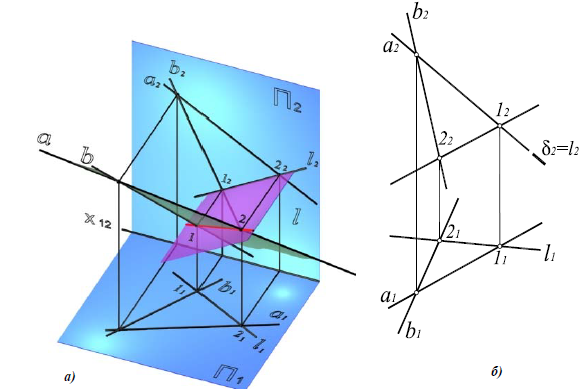
В соответствии с формулой р=2+2-3=1 пересечение двух плоскостей должно привести к появлению одномерного объекта, т.е. прямой линии. Для построения линии пересечения двух плоскостей общего положения (Р и 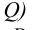достаточно найти две точки, одновременно принадлежащие этим плоскостям. В случае задания плоскостей следами (в соответствие с рисунком 4.7) решение очевидно.

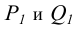
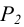
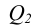
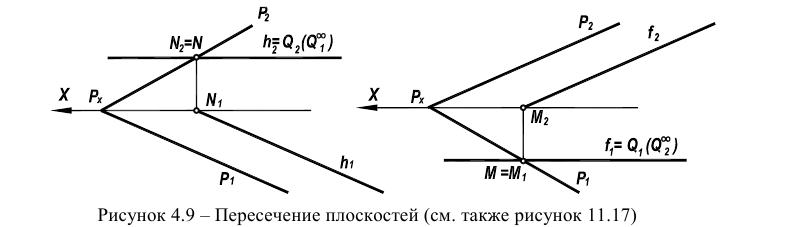
Пересечение горизонтальных следов дает возможность определить положение одной общей точки М, а пересечение фронтальных следов и

— другой общей точки N. Линия NM по определению лежит одновременно в двух плоскостях и, следовательно, она является линией пересечения.

При пересечении плоскости общего положения плоскостью уровня в сечении получается соответствующая линия уровня (рисунок 4.9).

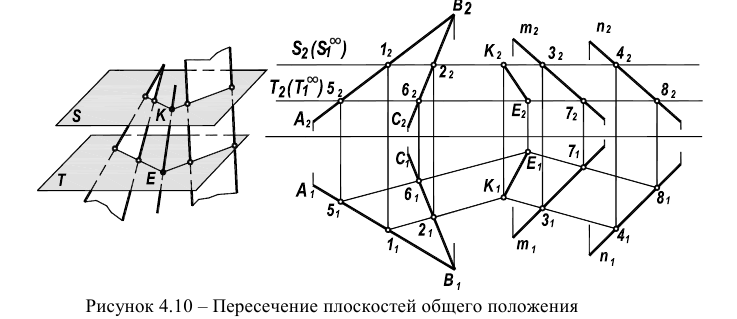
Определение линии пересечения двух плоскостей для других случаев, например, при задании плоскостей треугольником (симплексом) и параллельными прямыми, базируется на следующей идее. Три плоскости всегда пересекаются в одной точке. Следовательно, введение дополнительной плоскости к двум, уже имеющимся, позволит определить точку, одновременно принадлежащую заданным плоскостям. Проиллюстрируем это на рисунке 4.10.
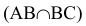
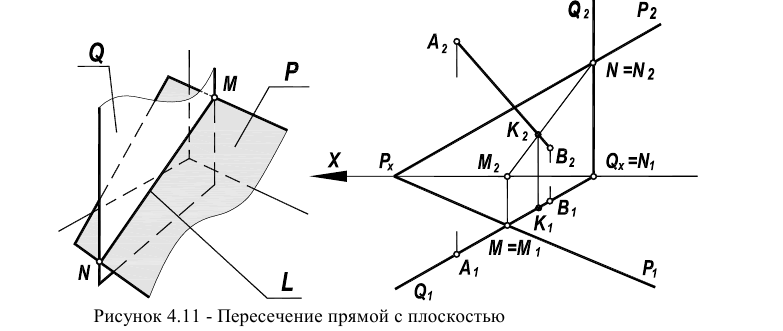
Две плоскости, заданные параллельными и пересекающимися прямыми, пересекаются по прямой ЕК, найденной с помощью секущих плоскостей уровня S и Т. Плоскость S пересекает по прямой 12, а плоскость (m//n) по прямой 34. На пересечении прямых 12 и 34 отмечается точка К. Аналогично строится точка Е, полученная с помощью секущей плоскости Т.

Пересечение прямой и плоскости

Пересечением прямой и плоскости в пространстве является точка, что подтверждается и вычислением по формуле р=1 +2-3=0.

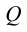
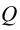
Прямая L в пространстве (в соответствии с рисунком 4.11) может рассматриваться как результат пересечения проецирующих плоскостей и Р. При этом проекции прямой нужно рассматривать как соответствующие следы этих плоскостей и Р.

Параллельность

Частным случаем пересечения прямых и плоскостей является взаимная параллельность. В трехмерном пространстве отсутствует полная параллельность. Понятие параллельности вводится с помощью признаков (условий).

При параллельности пересечением является несобственный элемент.
Признак параллельности прямых следует непосредственно из определения пересечения прямых (раздел 2.1). В соответствии с рисунком 4.13 одноименные проекции параллельных прямых попарно параллельны (параллельные прямые пересекаются в несобственной точке).

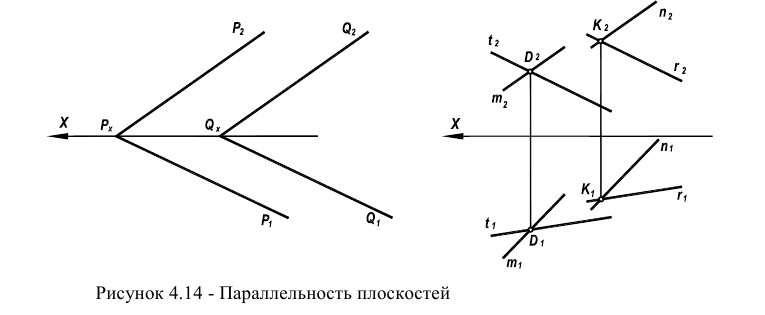
Признаком параллельности плоскостей является то, что две пересекающиеся прямые одной плоскости должны быть параллельны двум пересекающимся прямым другой плоскости (рисунок 4.14).

Такими прямыми могут быть следы. В этом случае одноименные следы должны быть параллельны между собой

В любом другом случае (в соответствии с рисунком 4.14) должна соблюдаться параллельность пересекающихся прямых, образующих плоскости,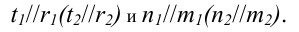

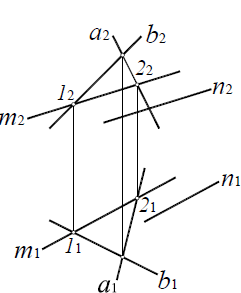
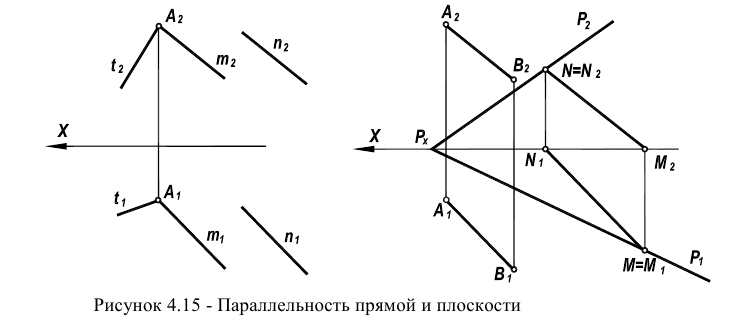
Параллельность прямой и плоскости должны отвечать следующему условию: прямая параллельна плоскости, если она параллельна одной из прямых этой плоскости. В соответствии с вышесказанным и рисунком 4.15 проекции

пространственной прямой должны быть параллельны соответствующим проекциям прямой, лежащей в плоскости.

Прямая n параллельна прямой m, лежащей в плоскости 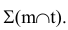Прямая АВ параллельна прямой MN, лежащей в плоскости Р, заданной следами.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник