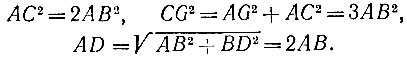Как построить перпендикуляр на местности
Три варианта построения прямого угла на местности. Как проверить угол уже построенного дома, когда замер диагоналей невозможен?
В данной статье описываются три распространенных варианта построения прямых углов при разметке участка для будущего дома, а также описываются методы проверки углов уже возведенных зданий и сооружений без доступа к замеру их диагоналей.
На самом же деле, вариантов существует множество и большинство из них выражаются через тригонометрические функции или с помощью сложных геометрических построений, но здесь это ни к чему, на стройплощадке ни один строитель не возьмется за сложные вещи, упуская время.
Поэтому, рассмотрим три самых простых, но тем не менее надежных метода построения прямых углов:
Теорема Пифагора
Это самый часто используемый и очень надежный способ.
Теорема Пифагора устанавливает соотношение между сторонами прямоугольного треугольника и звучит так: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Для построения прямого угла можно воспользоваться готовым решением (рисунок ниже) или же зная стороны дома, можно без труда вычислить значение диагонали для своего дома и в дальнейшем работать с полученным значением.
Основное соотношение сторон треугольника Пифагора — 3, 4 и 5 единиц. Для удобства, существуют производные треугольники от основного, получаемые при умножении сторон треугольника Пифагора на какой-либо коэффициент. К примеру, стороны 3,4,5 умноженные на К=2 (коэффициент 2), дают треугольник со сторонами 6,8,10, при К=3, стороны 9,12,15 и т.д.
Геометрическое построение
Данный способ ни чуть не хуже Пифагорова треугольника, но редко используемый (в силу забывчивости школьных знаний), хотя очень даже эффективный!
Выглядит сложнее, чем на самом деле.
Зная угол здания (точка О), отмечаем две точки О1 и О2 по оси А, равноудаленные от точки О. Одинаковое расстояние откладывается с помощью рулетки.
Точки О1 и О2 являются центрами окружностей одинакового радиуса. Прямая, проведенная через точку пересечения двух окружностей (точка В) и точку О будет давать прямой угол с прямой А.
По факту, этот способ ни чуть не хуже треугольника Пифагора, имея под рукой два колышка и отрезок веревки, построение осей будущего дома производится всего за 20-40 минут в зависимости от размера и сложности здания.
Две рулетки
Вместо построения окружностей из точек О1 и О2, используются две рулетки (рулетки без погрешности между собой, допустимое отклонение 2-3 мм. на 10 м. по размерной шкале) и прикладываются нулевой отметкой к каждой из точек О1 и О2.
Далее, совмещаем их одинаковыми значениями по мерным шкалам (точка Х) и получаем точку Х, соединив которую с точкой О получим перпендикуляр. В данном случае, построен равнобедренный треугольник, где его высота делит основание ровно пополам и образует с ним прямой угол.
На практике это делается следующим образом: отмечается три контрольные точки по двум рулеткам на пересечении делений (к примеру 1 м., 3м. и 7м.). Далее, через них протягивается разметочный шнур из точки О. Если все точки пересечения шкал лежат на одной прямой (совпадают со шнуром), то построение выполнено верно.
Это настолько быстро делается, что на первый взгляд может показаться неправдоподобным, но поверьте — геометрия работает со 100% гарантией.
Проверка прямого угла построенного здания
Все вышеописанные способы так же применимы и к уже стоящим зданиям. Они используются как проверка за строителями, а так же в случаях, если требуется сооружать фундамент по периметру старого дома и/или ровно облицевать ветхий домик каким-либо материалом.
Все действия аналогичны и главное правило заключается в том, чтобы вынести замеры за пределы строения.
Используя бечевку, протягиваем ее параллельно стенам и закрепляем колышками, а после — снимаем замер.
При геометрическом построении, точка пересечения двух окружностей будет лежать не в основании стены, а по «невидимому» продолжению стены в её же плоскости (на рисунке обозначена точкой Х).
При необходимости, все способы свободно комбинируются или взаимозаменяются.
На этом всё, спасибо Вам за уделенное внимание!
§ 9. Простейшая геометрия на местности
Во-первых, откажемся от проведения настоящих прямых на земле. Будем эти прямые прокладывать, т. е. отмечать на них, например, колышками, достаточно густую сеть точек. Для практических нужд этого обычно хватает, поскольку передвижение по прямой от одного колышка к другому, расположенному на близком расстоянии от первого,- действие, вполне осуществимое.
При указанных двух ограничениях, не пользуясь к тому же транспортиром, работать, конечно, трудно, но все же попробуйте решить предложенные ниже задачи!
На местности колышками обозначены две удаленные друг от друга точки. Как проложить через них прямую и, в частности, как можно без помощника устанавливать колышки на прямой между данными точками?
На местности колышками обозначены две точки одной прямой и две точки другой прямой. Как найти точку пересечения этих прямых?
На местности обозначены точки A и В. Найдите точку С, симметричную точке A относительно точки В.
На местности обозначены три данные точки A, В и С, не лежащие на одной прямой. Через точку A проложите прямую, параллельную прямой ВС.
Найдите середину отрезка AВ, заданного на местности двумя точками A и В.
Отрезок, заданный на местности двумя точками A и В, требуется разделить в отношении, в котором находятся длины двух отрезков KL и MN, заданных на местности точками К, L и М, N. Как это сделать?
На местности обозначены три точки A, М и N, не лежащие на одной прямой. Проложите биссектрису угла MAN.
Проложите на местности какую-нибудь прямую, перпендикулярную прямой, проходящей через заданные точки A и В. Как проложить перпендикуляр к прямой АВ, проходящий через данную точку Я?
На местности обозначены точки A и В. Найдите точки С, D и В, для которых выполнены равенства ∠ ВAС = 45°, ∠ BAD = 60° ∠ ВAE = 30°.
Решения
9.2. Пользуясь зрительным эффектом, указанным в решении задачи 9.1, легко найти точку пересечения прямых в том случае, если сразу ясно, что она лежит на продолжениях своих отрезков с концами в данных точках. В противном случае достаточно сначала проложить одну или обе прямые так, чтобы на каждой из них с одной стороны от предполагаемой точки пересечения были отмечены по две точки.
9.3. Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Для этого понадобится измерить в подходящих единицах длины расстояние между точками А и В.
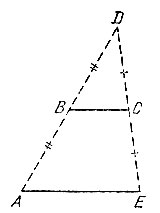
9.4. Продолжим прямую АВ за точку В и отложим на ней точку D на расстоянии АВ от точки В (рис. 8). Продолжим прямую CD за точку С и отложим на ней точку Е на расстоянии CD от точки С. Тогда отрезок АЕ будет параллелен отрезку ВС, являющемуся средней линией треугольника ADE. Заметим, что предложенный способ выгодно отличается от множества других способов, опирающихся на измерение углов или на деление отрезка пополам.
Рис. 8
Рис. 9
Быть может, приведенный способ нахождения середины отрезка покажется вам не самым простым. Однако его преимущества хорошо проявляются в следующей задаче, решив которую вы сможете делить отрезок не только на две, но и на любое число равных частей.
Рис. 10
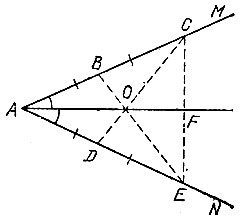
Найдем точку О пересечения прямых BE и CD. Тогда прямая АО будет искомой биссектрисой, поскольку в равнобедренном треугольнике АСЕ биссектриса AF является одновременно и медианой, а значит, проходит через точку О пересечения медиан ЕВ и CD.
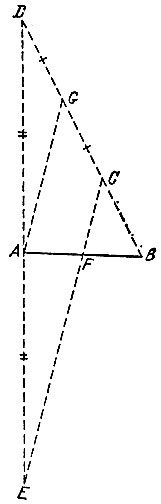
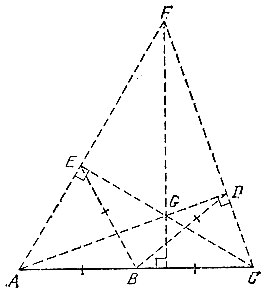
9.8. Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Кроме того, отложим на том же расстоянии от точки В еще две точки D и Е в двух разных, но не противоположных направлениях (рис. 11). Найдем точку F пересечения прямых АЕ и CD, а также точку G пересечения прямых AD и СЕ.
Рис. 11
9.9. Проложим перпендикуляр к прямой АВ (см. задачу 9.8), пересекающий в какой-то точке луч АВ. Без ограничения общности считаем для удобства, что эта точка пересечения и есть точка В. На перпендикуляре по разные стороны от точки В отложим точки С и F (рис. 12), удаленные от точки В на расстояние АВ. Тогда угол ВАС равен 45° (из равнобедренного прямоугольного треугольника ABC). На прямой AF отложим точку G на расстоянии АВ от точки А, а затем на прямой ВС отложим точку D на расстоянии CG от точки В. Тогда угол BAD равен 60Q, так как по теореме Пифагора для прямоугольных треугольников ABC, ACG и ABD имеют место равенства
Рис. 12
Для построения точки Е теперь остается проложить биссектрису угла BAD (см. задачу 9.7).
Как провести перпендикуляр к прямой — правило построения
Перпендикуляр — это прямая линия, пересекающая другую линию под углом 90°. Построением перпендикуляров на начальном уровне занимаются школьники на уроке геометрии. В будущем эти знания могут пригодиться как в быту, так и в профессиональной сфере. Чтобы правильно провести перпендикуляр к прямой, рекомендуется изучить все возможные способы. Они подразделяются на простые и сложные. Кроме того, для каждого из них потребуются определенные канцелярские принадлежности.
Использование транспортира
Одним из наиболее простых способов построения перпендикуляра к прямой является чертеж при помощи специального инструмента, который называется транспортир. Чтобы правильно начертить отрезок, необходимо по пунктам выполнить следующие действия:
Этот способ широко используется на уроках геометрии. Его преимущество заключается в быстром и простом построении. Для выполнения требуется только транспортир и простой карандаш.
Циркуль и линейка
Перпендикулярный луч можно опустить на отрезок при помощи еще одного незамысловатого способа. Для этого необходимы простой карандаш, линейка и циркуль. Построить прямой угол можно, выполнив следующие действия:
В результате этих действий должен получиться перпендикуляр, составляющий с прямой линией угол в 90°. Метод более сложный, если сравнивать его с первым. Его целесообразно использовать в том случае, если под рукой не оказалось транспортира.
Теорема Пифагора
Чтобы построить перпендикуляр по этому способу, мало знать одного определения, поскольку потребуется теорема Пифагора и ее доказательство. Наиболее распространенный вариант — свойство египетского треугольника со сторонами 5, 4 и 3.
От основной точки А необходимо отмерить и отметить отрезок, равный 3. В результате получается точка В. Далее необходимо построить две одинаковые окружности. При этом центр первой будет располагаться в А, а центр второй — в В. Отметка пересечения этих окружностей обозначается как С. Значит, искомый перпендикуляр — это линия, соединяющая две точки (А и С). Конечно, этот способ лучше посмотреть наглядно на картинке или показать в виде чертежа.
Эту тему проходят на геометрии в 7 классе. Школьники должны дать определение перпендикуляра к прямой. А на его основании построить линию его под углом 90°.
Геометрические построения на местности
Муниципальное образовательное учреждение
основная общеобразовательная школа №16
Руководитель: учитель математики первой квалификационной категории
§1. Построения на местности
В школе мы довольно подробно изучаем геометрические построения с помощью циркуля и линейки и решаем много задач. А как решить такие же задачи на местности? Ведь невозможно вообразить себе такой огромный циркуль, который мог бы очертить окружность школьного стадиона или линейку для разметки дорожек парка.
На практике картографам для составления карт, геодезистам для того, чтобы размечать участки на местности, например, для закладки фундамента дома, приходится использовать специальные методы.
Цель настоящего реферата – ознакомление с литературой по данной теме и изучение некоторых методов решения геометрических задач на местности.
§1. ПОСТРОЕНИЯ НА МЕСТНОСТИ
Знание геометрии и умение применять эти знания на практике полезно в любой профессии. Традиционно построения на местности производят геодезисты для съемки плана земельного участка и строители для закладки фундаментов. Однако, такие знания бывают довольно часто нужны и в других областях деятельности. Всемирно известный писатель Артур Конан Дойль был врачом. Но он очень хорошо, видимо, знал геометрию. В рассказе «Обряд дома Месгрейвов» он описал, как Шерлоку Холмсу нужно было определить, где будут конец тени от вяза, который срубили. Он знал высоту этого дерева ранее. Шерлок Холмс так объяснил свои действия: «… я связал вместе два удилища, что дало мне шесть футов, и мы с моим клиентом отправились к тому месту, где когда-то рос вяз. Я воткнул свой шест в землю, отметил направление тени и измерил ее. В ней было девять футов.
Дальнейшие мои вычисления были уж совсем несложны. Если палка высотой в шесть футов отбрасывает тень в девять футов, то дерево высотой в шестьдесят четыре фута отбросит тень в девяносто шесть футов, и направление той и другой, разумеется, будет совпадать».
Можно подумать, что работа на местности ничем существенно не отличается от работы циркулем и линейкой на обыкновенной бумаге. Но это не так. На местности расстояния между точками довольно велики и нет таких линеек и циркулей, которые могли бы помочь нам. Да и вообще чертить на земле какие-либо линии затруднительно. Таким образом, построения на местности, основываясь на геометрических законах, имеют свою специфику:
Во – первых, все прямые не проводятся на земле, а прокладываются, т. е. отмечается на них, например, колышками, достаточно густая сеть точек. Обычно прокладку прямых на местности называют провешиванием прямых.
Во – вторых, запрещается при построениях проводить какие–либо дуги. Поэтому, циркуля у нас фактически нет. Все, что остается от циркуля, это возможность откладывать на данных (проложенных) прямых конкретные расстояния, которые должны быть заданы не численно, а с помощью двух точек, уже обозначенных колышками, где-то на местности. Сами расстояния будут измеряться шагами, ступнями, пальцами рук, или любыми подходящими для этой цели предметами.
При геодезических работах используются специальные колышки длиной 15-20 см и диаметром 2-3 см, в торец которых забиваются гвоздики для более точного обозначения концов отмеряемого отрезка, и вехи – деревянные заостренные шесты длиной 1,5-2 м и диаметром 2-4 см.
Как правило, участки местности представляют собой не идеально ровную поверхность, как тетрадный лист, на земле есть возвышения и углубления. Чтобы они не искажали геометрические образы прокладываемых линий, на местности строят не наклонные отрезки, а их ортогональные проекции на горизонтальную плоскость – горизонтальные проложения. Их можно определить, зная угол наклона – угол, образованный линией местности и ее проекцией на горизонтальную плоскость. Эти углы измеряются специальными приборами эклиметрами.
Задача 1. Проложить прямую
На местности колышками обозначены две удалённые друг от друга точки. Как проложить через них прямую и, в частности, как можно без помощника устанавливать колышки на прямой между данными точками?
Задача 2. Точка пересечения прямых
На местности колышками обозначены две точки одной прямой и две точки другой прямой. Как найти точку пересечения этих прямых?
Пользуясь зрительным эффектом, указанным в решении задачи 1, легко найти точку пересечения прямых в том случае, если сразу ясно, что она лежит на продолжениях обоих отрезков с концами в данных точках. В противном случае достаточно сначала проложить одну или обе прямые так, чтобы на каждой из них с одной стороны от предполагаемой точки пересечения были отмечены по две точки.
Задача 3. Симметрия относительно точки
На местности обозначены точки А и В. Найдите точку С, симметричную точке А относительно точки В.
Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Для этого понадобится измерить в подходящих единицах длины расстояние между точками А и В.
Задача 4. Параллельная прямая
На местности обозначены три данные точки: А, В и С, не лежащие на одной прямой. Через точку А проложите прямую, параллельную прямой ВС.
Продолжим прямую АВ за точку В и отложим на ней точку D на расстоянии АВ от точки В. Продолжим прямую СD за точку С и отложим на ней точку Е на расстоянии СD от точки С. Тогда отрезок АЕ будет параллелен отрезку ВС, являющемуся средней линией треугольника АDЕ. Заметим, что предложенный способ выгодно отличается от множества других способов, опирающихся на измерение углов или на деление отрезка пополам.
Задача 5. Нахождение середины отрезка.
Найдите середину отрезка АВ, заданного на местности двумя точками А и В.
Задача 6. Деление отрезка в данном отношении
Отрезок, заданный на местности двумя точками А и В, требуется разделить в отношении, в котором находятся длины двух отрезков KL и MN, заданных на местности точками K, L и M, N. Как это сделать?
Задача 7. Построение биссектрисы угла
На местности обозначены три точки A, M и N, не лежащие на одной прямой. Проложите биссектрису угла MAN.
Найдём точку О пересечения прямых ВЕ и CD. Тогда прямая АО будет искомой биссектрисой, поскольку в равнобедренном треугольнике ACE биссектриса AF является одновременно и медианой, а значит, проходит через точку О пересечения медиан EB и CD.
Задача 8. Построение перпендикуляра к прямой
Проложите на местности какую-нибудь прямую, перпендикулярную прямой, проходящей через заданные точки А и В. Как проложить перпендикуляр к прямой АВ, проходящей через данную точку H?
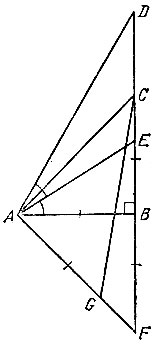
Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Кроме того, отложим на том же расстоянии от точки В ещё две точки D и E в двух разных, но не противоположных направлениях. Найдём точку F пересечения прямых AE и CD, а также точку G пересечения прямых AD и CE. Прямая FG перпендикулярна прямой АВ. Действительно, точка А, Е,D и С равноудалены от точки В, т. е. лежат на одной окружности с центром В и диаметром АС. Следовательно, вписанные углы ADC и AEC прямые, поэтому AD и CE – высоты треугольника AFC. Так как все три высоты этого треугольника пересекаются в одной точке G, то прямая FG перпендикулярна стороне АС. Для того чтобы проложить перпендикуляр к прямой АВ через данную точку H, достаточно теперь проложить через эту точку прямую, параллельную прямой FG.
Задача 9. Построения под заданным углом
На местности обозначены точки А и В. Найдите точки C, D и E, для которых выполнены равенства 


Проложим перпендикуляр к прямой АВ, пересекающий в какой–то точке луч АВ. Без ограничения общности считаем для удобства, что эта точка пересечения и есть точка В. На перпендикуляре по разные стороны от точки В отложить точки С и F, удалённые от точки В на расстояние АВ. Тогда угол ВАС равен 45° (из равнобедренного прямоугольного треугольника АВС). На прямой AF отложим точку G на расстоянии АВ от точки А, а затем на прямой ВС отложим точку D на расстоянии CG от точки В. Тогда угол ВАD равен 6О°, так как по теореме Пифагора для прямоугольного треугольников АВС, ACG и ABD имеют место равенства
Для построения точки Е теперь остаётся проложить биссектрису угла BAD.
Задача 10. Измерение высоты дерева.
Высоту деревьев можно определить при помощи шеста. Этот способ состоит в следующем.
Расстояния bc, aC легко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние CD (которое также измеряется непосредственно), чтобы узнать искомую высоту дерева.
В настоящем реферате рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями на местности – провешиванием прямых, делением отрезков и углов, измерением высоты предмета. Приведены задачи и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ. Ценно то, что для их решения не требуется знаний больших, чем в объеме 8 классов.
Таким образом, цель реферата – изучение методов геометрических построений на местности – достигнута
3. «Методы геометрических построений», М., Учпедгиз, 1952.