Как построить перпендикуляр к плоскости
Как построить перпендикуляр к плоскости
Контрольные задания по теме: Рабочая тетрадь задача 44, задача 45
Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.
Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.

Рисунок 28

Рисунок 29
На рисунке 29 изображено построение перпендикуляра КF к плоскости АВС.
Две плоскости перпендикулярны, если прямая, лежащая в одной плоскости, перпендикулярна двум пересекающимся прямым другой плоскости. Построение плоскости перпендикулярной данной плоскости АВС показано на рисунке 30. Через точку М проводится прямая МN, перпендикулярная плоскости АВС. Горизонтальная проекция этой прямой перпендикулярна АС, так как АС является горизонталью, а фронтальная проекция перпендикулярна АВ, так как АВ – фронталь. Затем через точку М проводится произвольная прямая EF. Таким образом, плоскость перпендикулярна АВС и задана двумя пересекающимися прямыми EF и MN.

Рисунок 30
Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.
Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.

Рисунок 31
1. Сформулируйте теорему о свойстве прямого угла.
2. В каком случае прямая перпендикулярна плоскости?
3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства?
4. Для чего применяется способ прямоугольного треугольника?
5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Алгоритм построения перпендикуляра к плоскости
Перпендикулярность прямой и плоскости
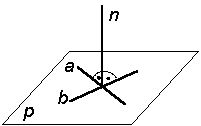
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (рис. 6.3).
Если прямая перпендикулярна плоскости, то она будет перпендикулярна любой прямой, лежащей в этой плоскости. Из множества этих прямых при построении перпендикуляров к плоскости выбирают горизонталь и фронталь плоскости. В этом случае, пользуясь свойством проецирования прямого угла на комплексном чертеже, фронтальную проекцию перпендикуляра проводим под углом 90 0 к фронтальной проекции фронтали, а горизонтальную проекцию перпендикуляра – под углом 90° к горизонтальной проекции горизонтали.
Рассмотрим алгоритм построения перпендикуляра n к плоскости Р(D АВС) (табл. 6.6).
| Вербальная форма | Графическая форма |
| 1. Для того чтобы построить перпендикуляр к плоскости Р(D АВС) через точку D, необходимо сначала построить любую горизонталь в данной плоскости Р(D АВС) – h (h1h2) | 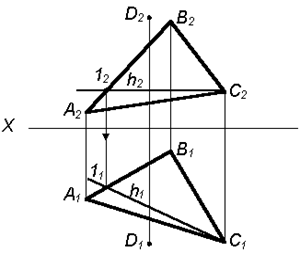 |
| 2. Строим фронталь в плоскости Р(D АВС) – f ( f1f2) | 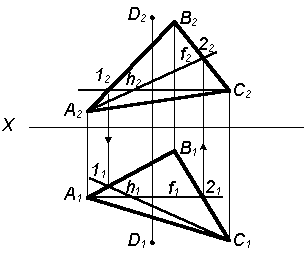 |
3. Строим перпендикуляр n к плоскости Р(D АВС). Для этого через точку D2 проводим n2, перпендикулярно f2, а через D1 проводим n1, перпендикулярно h1. n (n1n2) ^Р (DАВС), так как n1^h1; h1  P1 ( DА1В1С1) n2^f2; f2 P1 ( DА1В1С1) n2^f2; f2 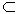 P2 (DА2В2С2) P2 (DА2В2С2) | 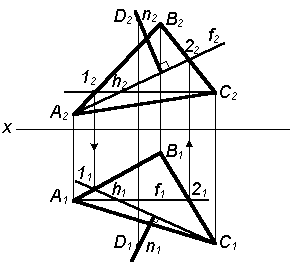 |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Построение перпендикуляра к плоскости, проходящего через заданною точку
Известно, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости. При построении перпендикуляра в качестве таких двух пересекающихся прямых плоскости используются линии уровня плоскости (фронтали и горизонтали). Это связано с тем, что согласно теоремы о проецировании прямого угла, именно с этими прямыми сохраняется прямой угол на плоскостях проекциях.
Пример построения перпендикуляра к плоскости, проходящего через заданною точку (рис. 59).
Постановка задачи. Задана плоскость α треугольником ∆АВС и точка К. Построить перпендикуляр т к плоскости α, проходящей через точку К. Координаты точек: А(75; 50; 20), В(30; 10; 55), С(5; 30;10) и К(45; 5; 10).
1. В плоскости α проводится горизонталь h: hÌα и h‖π1.
2. Используя теорему о прямом угле строится первая проекция перпендикуляра m: m1⊥h1 и К1⊂m1.
3. В плоскости α проводится фронталь f: fÌα и f‖π2.
4. Используя теорему о прямом угле строится вторая проекция перпендикуляра m: m2⊥f2 и К2⊂m2.
Варианты заданий приведены в табл. 9.
Построение прямой параллельной заданной плоскости
Известно, что если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Построение прямой параллельно заданной плоскости основывается на использовании этого утверждения и инварианта параллельности прямых.
Пример построения (рис. 60).
Постановка задачи. Задана плоскость α треугольником ∆АВС и точка М не принадлежащая этой плоскости. Координаты точек: А(75; 50; 20); В(30; 10; 55); С(5; 30;10) и М(45; 30; 30).
Построить прямую l параллельную плоскости α, проходящую через точку М.
1. В заданной плоскости α выбирают или строят прямую, которая принадлежит этой плоскости (в примере выбрана сторона АС треугольника ∆АВС).
Варианты заданий приведены в табл. 9.
Исходные данные по темам «Перпендикулярность и параллельность прямой и плоскости»
| Вариант | Численные значения координат точек | |||||||||||||
| А | В | С | К | М | ||||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | x | y | z |
продолжение табл. 9
| Вариант | Численные значения координат точек | |||||||||||||
| А | В | С | К | М | ||||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | x | y | z |
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Как построить перпендикуляр к плоскости
Контрольные задания по теме: Рабочая тетрадь задача 44, задача 45
Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.
Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.
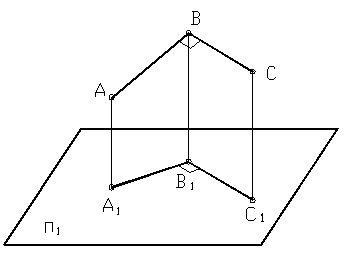
Рисунок 28
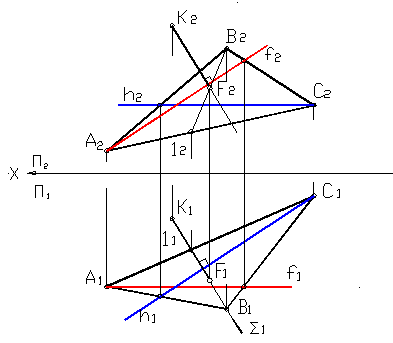
Рисунок 29
На рисунке 29 изображено построение перпендикуляра КF к плоскости АВС.
Две плоскости перпендикулярны, если прямая, лежащая в одной плоскости, перпендикулярна двум пересекающимся прямым другой плоскости. Построение плоскости перпендикулярной данной плоскости АВС показано на рисунке 30. Через точку М проводится прямая МN, перпендикулярная плоскости АВС. Горизонтальная проекция этой прямой перпендикулярна АС, так как АС является горизонталью, а фронтальная проекция перпендикулярна АВ, так как АВ – фронталь. Затем через точку М проводится произвольная прямая EF. Таким образом, плоскость перпендикулярна АВС и задана двумя пересекающимися прямыми EF и MN.
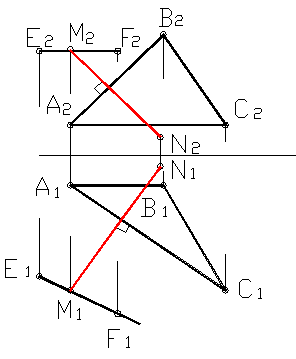
Рисунок 30
Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.
Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.
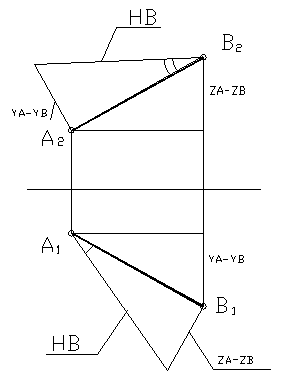
Рисунок 31
1. Сформулируйте теорему о свойстве прямого угла.
2. В каком случае прямая перпендикулярна плоскости?
3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства?
4. Для чего применяется способ прямоугольного треугольника?
5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Как построить перпендикуляр к плоскости
Из всех возможных положений прямой, пересекающей плоскость, отметим случай, когда прямая перпендикулярна к плоскости, и рассмотрим свойства проекций такой прямой.
На рис. 185 задана плоскость, определяемая двумя пересекающимися прямыми AN и AM, причем AN является горизонталью, а AM — фронталью этой плоскости. Прямая АВ, изображенная на том же чертеже, перпендикулярна к AN и к AM и, следовательно, перпендикулярна к определяемой ими плоскости.
Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости. Но чтобы при этом проекция перпендикуляра к плоскости общего положения оказалась перпендикулярной к одноименной проекции какой-либо прямой этой плоскости, прямая должна быть горизонталью, или фронталью, или профильной прямой плоскости. Поэтому, желая построить перпендикуляр к плоскости, берут в общем случае две такие прямые (например, горизонталь и фронталь, как это показано на рис. 185).
Итак, у перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проекции фронтали, профильная проекция перпендикулярна к профильной проекции профильной прямой этой плоскости.
Очевидно, в случае, когда плоскость выражена следами (рис. 186), мы получаем следующий вывод: если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна к горизонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоскости.
Итак, если в системе π1 п2 горизонтальная проекция прямой перпендикулярна к горизонтальному следу и фронтальная проекция прямой перпендикулярна к фронтальному следу плоскости, то в случае плоскостей общего положения (рис. 186), а также горизонтально и фронтально-проецирующих прямая перпендикулярна к плоскости. Но для профильно-проецирующей плоскости может оказаться, что прямая к этой плоскости не перпендикулярна, хотя проекции прямой соответственно перпендикулярны к горизонтальному и фронтальному следам плоскости. Поэтому в случае профильно-проецирующей плоскости надо рассмотреть также взаимное положение профильной проекции прямой и профильного следа данной плоскости и лишь после этого установить, будут ли перпендикулярны между собой данные прямая и плоскость.
Очевидно (рис. 187), горизонтальная проекция перпендикуляра к плоскости сливается с горизонтальной проекцией линии ската, проведенной в плоскости через основание перпендикуляра.
На рис. 188 показано построение перпендикуляра к плоскости, определяемой треугольником АВС. Перпендикуляр проведен через точку А.
Так как фронтальная проекция перпендикуляра к плоскости должна быть перпендикулярна к фронтальной проекции фронтали плоскости, а его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, то в плоскости через точку А проведены фронталь с проекциями A’D’ и A»D» и горизонталь А»Е», А’Е’. Конечно, эти прямые не обязательно проводить именно через точку А.
Далее проведены проекции перпендикуляра: M»N» ⊥ A»D», M’N’ ⊥ А’Е’. Почему проекции на рис. 188 на участках A»N» и А’М’ показаны штриховыми линиями? Потому, что здесь рассматривается плоскость, заданная треугольником АВС, а не только этот треугольник: перпендикуляр находится частично перед плоскостью, частично за ней.
На рис. 189 и 190 показано построение плоскости, проходящей через точку А перпендикулярно к прямой ВС. На рис. 189 плоскость выражена следами. Построение начато с проведения через точку А горизонтали искомой плоскости: так как горизонтальный след плоскости должен быть перпендикулярен к В’С’ то и горизонтальная проекция горизонтали должна быть перпендикулярна к В’С’. Поэтому A’N’ ⊥ В’С. Проекция A»N» || оси х, как это должно быть у горизонтали. Затем проведен через точку N» (N» — фронтальная проекция фронтальною следа горизонтали AN) след f’0a ⊥ »ѻ, получена точка Хa и проведен след h’0a || A’N’ (h’0a ⊥ В’С’).
На рис. 190 плоскость определена ее фронталью AM и горизонталью AN. Эти прямые перпендикулярны к ВС (А»М» ⊥ »ѻ, A’N’ ⊥ В’С); определяемая ими плоскость перпендикулярна к ВС.
Так как перпендикуляр к плоскости перпендикулярен к каждой прямой, проведенной в этой плоскости, то, научившись проводить плоскость перпендикулярно к прямой, можно воспользоваться этим для проведения перпендикуляра из некоторой точки А к прямой общего положения ВС. Очевидно, можно наметить следующий план построения проекций искомой прямой:
1) через точку А провести плоскость (назовем ее ϒ), перпендикулярную к ВС;
2) определить точку К пересечения прямой ВС с пл. ϒ;
3) соединить точки А и К отрезком прямой линии.
Прямые АК и ВС взаимно перпендикулярны.
Пример построения дан на рис. 191. Через точку А проведена плоскость (ϒ), перпендикулярная к ВС. Это сделано при помощи фронтали, фронтальная проекция A»F» которой проведена перпендикулярно к фронтальной проекции »ѻ и горизонтали, горизонтальная проекция которой перпендикулярна к В’С’.
Затем найдена точка К, в которой прямая ВС пересекает пл. ϒ. Для этого через прямую ВС проведена горизонтально-проецируюшая плоскость β (на чертеже она задана только горизонтальным следом β’). Пл. β пересекает пл. ϒ по прямой с проекциями 1’2‘ и 1″2″. В пересечении этой прямой с прямой ВС получается точка К. Прямая АК является искомым перпендикуляром к ВС. Действительно, прямая АК пересекает прямую ВС и находится в пл. ϒ, перпендикулярной к прямой ВС; следовательно, АК ⊥ ВС.
На рис. 192 изображены плоскость общего положения а, проходящая через точку А, и перпендикуляр AM к этой плоркости, продолженный до пересечения с пл. п1, в точке В’.
Угол ф1 между пл. а и пл. п1 и угол ф между прямой AM и пл. п1 являются острыми углами прямоугольного треугольника В’АМ’ и, следовательно, ф1 +ф = 90°. Аналогично, если пл. а составляет с пл. п2 угол σ2, а прямая AM, перпендикулярная к а, составляет с пл. п2 угол σ, то σ2 + σ = 90°. Из этого, прежде всего, следует, что плоскость общею положения, которая должна составлять с пл. п1 угол ф1 а с пл. п2 угол σ2, может быть построена, лишь если 180° > Ф1 + σ2 > 90°.
Действительно, складывая почленно Ф1 + Ф = 90° и σ2 + σ = 90°, получим Ф1 + σ2 + Ф + σ = 180°, т. е. Ф1 + σ2 90°. Если взять Ф1 + σ2 =90°, то получится профильно-проецирующая плоскость, а если взять Ф1 + σ2 = 180°, то получится профильная плоскость, т. е. в обоих этих случаях плоскость не общего положения, а частного.
ПОСТРОЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЕЙ
Построение плоскости β, перпендикулярной к плоскости a, может быть произведено двумя путями: 1) пл. β проводится через прямую, перпендикулярную к пл. а; 2) пл. β проводится перпендикулярно к прямой, лежащей в пл. а или параллельной этой плоскости. Для получения единственного решения требуются дополнительные условия.
На рис. 193 показано построение плоскости, перпендикулярной к плоскости, заданной треугольником CDE. Дополнительным условием здесь служит то, что искомая плоскость должна проходить через прямую А В. Следовательно, искомая плоскость определяется прямой АВ и перпендикуляром к плоскости треугольника. Для проведения этого перпендикуляра к пл. CDE в ней взяты фронталь CN и горизонталь СМ: если B»F» ⊥ C“N» и B’F’⊥C’M’, то BF⊥ пл. CDE.
Образованная пересекающимися прямыми АВ и BF плоскость перпендикулярна к пл. СОЕ, так как проходит через перпендикуляр к этой плоскости. На рис. 194 горизонтально-проецирующая плоскость β проходит через точку К перпендикулярно к плоскости, заданной треугольником АВС. Здесь дополнительным условием являлась перпендикулярность искомой плоскости сразу к двум плоскостям: к пл. АВС и к пл. п1. Поэтому и ответом служит горизонтально-проецирующая плоскость. А так как она проведена перпендикулярно к горизонтали AD, т. е. к прямой, принадлежащей пл. АВС, то пл. β перпендикулярна к пл. АВС.
Может ли перпендикулярность одноименных следов плоскостей служить признаком перпендикулярности самих плоскостей?
К очевидным случаям, когда это так, относится взаимная перпендикулярность двух горизонтально-проецирующих плоскостей, у которых горизонтальные следы взаимно перпендикулярны. Также это имеет место при взаимной перпендикулярности фронтальных следов фронтально-проецирующих плоскостей; эти плоскости взаимно перпендикулярны.
Рассмотрим (рис. 195) горизонтально-проецирующую плоскость β, перпендикулярную к плоскости общего положения а.
Итак, перпендикулярность горизонтальных следов плоскости общего положения и горизонтально-проецирующей соответствует взаимной перпендикулярности этих плоскостей.
Очевидно, перпендикулярность фронтальных следов фронтально-проецирующей плоскости и плоскости общего положения также соответствует взаимной перпендикулярности этих плоскостей.
Но если одноименные следы двух плоскостей общего положения взаимно перпендикулярны, то самые плоскости не перпендикулярны между собой, так как здесь не соблюдается ни одно из условий, изложенных в начале этого параграфа.
В заключение рассмотрим рис. 196. Здесь имеет место случай взаимной перпендикулярности одноименных следов в обеих их парах и перпендикулярности самих плоскостей: обе плоскости особого (частного) положения — профильная ϒ и профильно-проецирующая а.