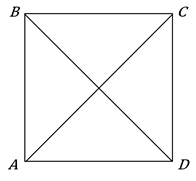
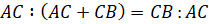Как построить параллелограмм 6 класс

Конспект урока по математике 6 класс по теме Параллелограмм

Базовый учебник : Учебник: Математика. Арифметика. Геометрия. 6 класс: учеб. для общеобразоват. учреждений с приложением на электронном носителе / Е.А. Бунимович и др. –2-е изд. – М.: Просвещение, 2013. – 223 с.: ил. – (Академический школьный учебник)

образовательная – обобщение и развитие знаний обучающихся о геометрических фигурах группы многоугольников и их свойствах, формирование навыка применения полученных знаний в жизненных ситуациях.

развивающая – развитие логического мышления, математического аппарата, познавательного интереса к предмету, самостоятельности; читательских компетенций.

воспитательная – формирование морально-этической стороны личности, эстетического сознания, научной эстетики; тренировка стрессоустойчивости.

— образовательные ( формирование познавательных УУД ) :

применять знания о многоугольниках, уметь выделять данный тип из многообразия геометрических фигур, определять их общие свойства, изображать их на плоскости.

— воспитательные ( формирование коммуникативных и личностных УУД ) :

умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи; понимать смысл поставленной задачи; слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

— развивающие ( формирование регулятивных УУД )

развивать умение анализировать, сравнивать, обобщать, делать выводы, самостоятельно ставить цели, развивать внимание, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

по источникам знаний: словесные, наглядные;

по степени взаимодействия учитель-ученик: эвристическая беседа;

относительно дидактических задач: подготовка к восприятию;

относительно характера познавательной деятельности: репродуктивный, частично-поисковый.

4. Планируемые результаты: Распознавать на чертежах рисунках в окружающем мире параллелограммы. Изображать параллелограммы с использованием чертежных инструментов. Исследовать свойства параллелограмма используя эксперимент, наблюдение, измерение, моделирование. Использовать компьютерное моделирование и эксперимент для изучения свойств параллелограмма. Формулировать, обосновывать и опровергать с помощью контрпримеров утверждения о свойствах параллелограмма. Сравнивать свойства параллелограмма различных видов: ромба, квадрата, прямоугольника.

5. Оборудование: Учебник: Математика. Арифметика. Геометрия. 6 класс: учеб. для общеобразоват. учреждений с приложением на электронном носителе / Е.А. Бунимович и др. –2-е изд. – М.: Просвещение, 2013. – 223 с.: ил. – (Академический школьный учебник) (Сферы), Тетрадь-тренажер Математика. Арифметика. Геометрия. 6 класс: пособие для учащихся общеобразовательных учреждений/ Е.А. Бунимович и др. – 3-е изд. – М.:Просвещение, 2013. – 128 с.: ил., мультимедиа проектор, компьютер, рабочие тетради учащихся, раздаточный материал (калька), циркуль.

6. Тип и особенности: урок открытия и изучения новых знаний через экспериментальную проверку, с помощью наблюдений. Урок в форме эвристической беседы

Технологическая карта урока математики в 6 классе по учебнику Е.А. Бунимовича.

Источник

Презентация по математике 6 класса на тему : » Параллелограмм»

Описание презентации по отдельным слайдам:

Разбейте прямые на 2 группы: 1) Пересекающиеся 2) непересекающиеся А) Б) В) Г) Д) Ж) З)

Пересекающиеся прямые 2) Непересекающиеся прямые k∩l x∩y s∩t g∩z z∩e Какими другими словами можно назвать непересекающиеся прямые? nꓵm cꓵd aꓵb eꓵg

2) Непересекающиеся прямые Какими другими словами можно назвать непересекающиеся прямые? Прямые, которые не пересекаются называются параллельными.

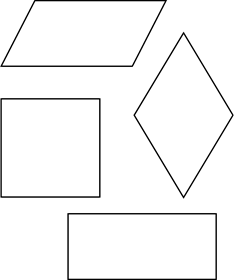
Из предложенных фигур выберете : 1)Фигуры, в которых нет пар параллельных прямых 2)Фигуры, в которых есть одна или более двух пар параллельных прямых 3) Фигуры, в которых есть 2 пары параллельных прямых. 1 3 8 2 10 5 6 4 7 9

1)Фигуры, в которых нет пар параллельных прямых 2)Фигуры, в которых есть одна или более двух пар параллельных прямых 3) Фигуры, в которых есть 2 пары параллельных прямых.

Тема : Параллелограмм Цели и задачи урока: 1)Определить какая фигура называется параллелограммом. 4)Узнать какие бывают виды параллелограммов. 2)Узнать какими свойствами обладает параллелограмм. 3) Узнать, как построить параллелограмм

Изучаем свойства (Эксперимент) Повернем параллелограмм вокруг точки О на 180 градусов при повороте противоположные стороны (углы) параллелограмма «поменялись местами», значит они равны. 3)Противоположенные стороны параллелограмма равны. Противоположенные углы равны Вывод: о

Физминутка Крепко зажмурить глаза на 3-5 секунд, а затем открыть их на такое же время. Повторять 5-6 раз Быстро моргать в течение 10-12 секунд, открыть глаза, отдыхать 10-12 секунд. Повторять 3 раза. Исходное положение: сидя, закрыть веки, массировать их с помощью легких круговых движений пальца. Повторять в течении 20-30 секунд.

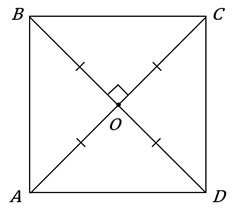
Свойства параллелограмма 1)Параллелограмм является центрально-симметричной фигурой. 2) Диагонали параллелограмма точкой пересечения делятся пополам. (АО=ОС, ОD=OB) 3)Противоположенные стороны параллелограмма равны. (АВ=СD, AD=BC) Противоположенные углы равны (˂A= ˂C, ˂B= ˂D)

Практическая работа (в тетради) Выполните построение параллелограмма 1 вариант 2 вариант 3 вариант АО=ОВ=ОС=ОD, AC BD АО=ОВ=ОС=ОD, AC BD AC BD АО=ОС, ОВ= ОD виды параллелограмма: прямоугольник, квадрат, ромб. Квадрат Прямоугольник Ромб Вывод: Каким свойством обладает прямоугольник? Каким свойством обладает ромб? Каким свойством обладает квадрат? Какие фигуры получились?

Работа с учебником №994 (устно) №998 Скопируйте параллелограмм в тетрадь (рис.12.8) и проведите их диагонали

ПАРАЛЛЕЛОГРАММ «мы повторили»

ПАРАЛЛЕЛОГРАММ «мЫ УЗНАли»

Домашнее задание (учебник) №996 №999 Представьте, что вам необходимо вырезать из листа бумаги ромб, а у вас нет никаких чертежных инструментов. Решите задачу с помощью перегибания листа бумаги. Подсказка. Воспользуйтесь тем, что у ромба две оси симметрии. №1003 Проведите в тетради две параллельные прямые, расстояние между которыми равно 3 см. Начертите какой−нибудь параллелограмм, одна пара сторон которого лежит на этих прямых и равна 4 см. Начертите прямоугольник, удовлетворяющий этим условиям а) Начертите в тетради, используя свойства клетчатой бумаги, какой−нибудь параллелограмм. б) Точки A, B и C − вершины параллелограмма, AB − его сторона (рис.12.9). Постройте точку D − четвертую вершину параллелограмма. Сколькими способами это можно сделать?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1275346

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Костромская область разработала программу привлечения педагогических кадров

Время чтения: 2 минуты

При детском омбудсмене в России создадут платформу для взаимодействия с родителями

Время чтения: 2 минуты

Московские школьники победили на международной олимпиаде по информатике

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Презентация по математике на тему «Построение параллелограмма.» (6 класс)

Описание презентации по отдельным слайдам:

Описание слайда:

ПОСТРОЕНИЕ ПАРАЛЛЕЛОГРАММА
Далее
Глава 12. Урок 151

Описание слайда:

Заполните «солнышко»:
Устная работа.
Далее
Устная работа.

Описание слайда:

Актуализация знаний.
Далее
– Что такое параллелограмм?
– Перечислите его свойства.
– Как можно построить параллелограмм, исходя из его определения?
Алгоритм.
а) Построить две параллельные
прямые.
б) Построить, пересекающие их
еще две параллельные прямые.

Описание слайда:

Далее
– Можно ли построить параллелограмм, исходя из его свойств?
– С помощью какого именно свойства можно построить параллелограмм?
– Какие инструменты нужны, чтобы построить параллелограмм по параллельным сторонам?
– Какие инструменты нужны, чтобы построить параллелограмм по диагоналям?
Актуализация знаний.

Описание слайда:

Далее
Формирование умений и навыков.
№ 1182. Постройте на нелинованной бумаге несколько различных параллелограммов с помощью: а) угольника и линейки; б) одной линейки.
Постройте параллелограмм, диагонали которого равны 5 см и 8 см.
Сколько параллелограммов с такими диагоналями можно построить?
Постройте другой параллелограмм с такими же диагоналями.

Описание слайда:

Далее
Формирование умений и навыков.
№ 1193. Постройте параллелограмм, диагонали которого равны 4 см и 5 см и пересекаются под углом 30°.
№ 1194. Постройте параллелограмм по заданным сторонам и диагонали

Описание слайда:

Далее
Формирование умений и навыков.
Постройте ромб, диагонали которого равны 3 см и 6 см.
Сколько ромбов с такими диагоналями можно построить?
Постройте ромб со стороной 5 см и углом между сторонами 60°.
Сколько ромбов с такими данными можно построить?

Описание слайда:

Далее
Формирование умений и навыков.
№ 1190. Диагонали прямоугольника равны, а диагонали квадрата не только равны, но и перпен­дикулярны друг другу.
а) Постройте прямоугольник, диагонали которого равны 6 см. Постройте другой прямоугольник с такими же диагона­лями.
б) Постройте квадрат с диагоналями, равными 8 см. Можно ли постро­ить другой квадрат с такими же диагоналями?

Описание слайда:

Далее
Формирование умений и навыков.
№ 1195. На рисунках а — г показаны способы построения прямоугольника, квадрата, ромба и параллелограмма. Опишите словами способ построения каждого четырехугольника и выполните построения.

Описание слайда:

Тест.
Далее
25) Можно построить несколько разных квадратов с данными диагоналями.
1) Параллелограмм – это фигура, у которой стороны параллельны.
2) Параллелограмм является четырехугольником.
3) У параллелограмма диагонали равны.
4) У параллелограмма все стороны равны.
5) У параллелограмма противоположные стороны равны.
6) Диагонали параллелограмма в точке пересечения делятся пополам.
7) Параллелограмм имеет ось симметрии.
8) Параллелограмм имеет центр симметрии.
9) Диагональ параллелограмма делит его на два равнобедренных треугольника.
10) Диагональ параллелограмма делит его на два равных треугольника.
11) Параллелограмм можно построить с помощью циркуля и линейки.
12) Можно построить только один параллелограмм с заданными диагоналями.
13) Ромб является параллелограммом.
14) Диагонали ромба в точке пересечения делятся пополам.
15) У ромба все углы равны.
16) Диагонали ромба равны.
17) Диагонали ромба перпендикулярны.
18) Прямоугольник не является параллелограммом.
19) Диагонали прямоугольника перпендикулярны.
20) Диагонали прямоугольника равны.
21) Диагонали квадрата перпендикулярны.
22) Диагонали квадрата равны.
23) Можно построить несколько разных ромбов с данными диагоналями.
24) Можно построить несколько разных прямоугольников с данными диагоналями.

Описание слайда:

Итоги урока.
Далее
– Что такое параллелограмм? Ромб? Прямоугольник? Квадрат?
– Перечислите свойства параллелограмма.
– Какое особое свойство имеют диагонали ромба? Прямоугольника? Квадрата?
– Как построить параллелограмм с помощью угольника и линейки? На чем основано это построение?
– Как построить параллелограмм с помощью линейки и циркуля? На чем основано это построение?
– Как можно построить ромб? Прямоугольник? Квадрат?
Домашнее задание.
1) № 1189.
2) Исследовательское задание. Рассмотреть все случаи построения параллелограмма, то есть по каким элементам он может быть построен. Оформить все эти случаи, выполнив построение на нелинованном листе бумаги.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Параллелограммы

Урок 21. Наглядная геометрия 5–6 классы ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Параллелограммы»

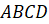
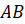
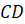
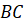
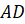
Проведём две пары параллельных прямых. Образованный при этом четырёхугольник назовём . У этого четырёхугольника сторона параллельна стороне , а сторона параллельна стороне . Такой четырёхугольник называется параллелограммом.

Запомните! Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

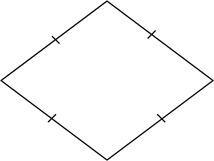
Посмотрите на следующие фигуры. Каждая из этих фигур является параллелограммом.

Ромб, прямоугольник и квадрат – тоже параллелограммы. Только это параллелограммы с некоторыми дополнительными свойствами.

Так, ромб – это параллелограмм, у которого все стороны равны.

А прямоугольник действительно является параллелограммом?

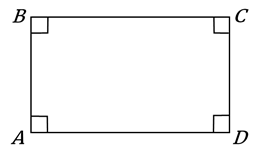
Прямоугольник – это параллелограмм, у которого все углы прямые.

Вспомним свойство, которое говорит о том, что два перпендикуляра к одной прямой, расположенные в одной плоскости, параллельны между собой.

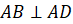
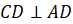
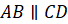
Так как у прямоугольника все углы прямые, то можем записать, что и . Значит, .

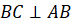
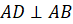
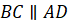
Также запишем, что и . А значит, .

Получилось, что у прямоугольника стороны попарно параллельны. Следовательно, прямоугольник 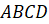является параллелограммом.

А вот квадрат – очень интересный четырёхугольник.

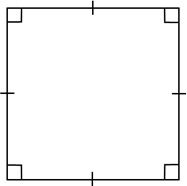
Как и у ромба, у квадрата все стороны равны. Только у него ещё все углы прямые. А значит, квадрат – это ромб, у которого все углы прямые.

Как и у прямоугольника, у квадрата все углы прямые. При этом у него ещё все стороны равны. Значит, квадрат – это прямоугольник, у которого все стороны равны.

Также у квадрата, как и у параллелограмма, стороны попарно параллельны. Только они ещё и равны. Все углы у квадрата прямые. А значит, квадрат – это параллелограмм с прямыми углами, у которого все стороны равны.

Таким образом, из этого следует, что квадрат – это параллелограмм, который одновременно является и прямоугольником, и ромбом.

Квадрат обладает рядом интересных свойств. Исследуем с вами квадрат и отыщем его свойства. Но прежде проведём отрезок, который соединяет две противоположные вершины квадрата. Такой отрезок называется диагональю квадрата. У квадрата две диагонали.

Сравним диагонали по длине.

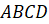
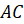
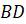
Давайте возьмём квадрат . Проведём диагонали и . Измерим с помощью линейки длину каждой диагонали. Их длины равны.

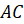
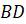
Выясним, как диагонали расположены одна относительно другой. Для этого возьмём чертёжный угольник. Совместим точку пересечения диагоналей с вершиной прямого угла угольника и расположим его так, чтобы одна из диагоналей совпала со стороной прямого угла угольника. Видим, что вторая диагональ квадрата совпала со второй стороной прямого угла угольника, а значит, диагонали и взаимно перпендикулярны.

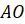
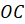
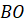
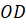
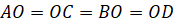
Теперь выясним, на какие части делятся диагонали квадрата точкой пересечения. Обозначим пересечение диагоналей квадрата точкой О. Измерим с помощью линейки отрезки и , и . Длины этих отрезков равны: . А значит, диагонали квадрата точкой пересечения делятся пополам.

Сформулируем основные свойства квадрата. Все углы квадрата прямые. Диагонали квадрата равны, взаимно перпендикулярны и точкой пересечения делятся пополам.

Сейчас проведём эксперимент. Возьмём лист бумаги в форме квадрата. Проведём диагональ. Она разделила квадрат на два треугольника. Эти треугольники равны.

Проверим это. Перегнём лист бумаги по диагонали. Видим, что треугольники, на которые диагональ делит квадрат, совпали при наложении, а значит, они равны.

Таким же образом можно проверить равенство треугольников, на которые делит квадрат его вторая диагональ.

Итак, сформулируем ещё одно свойство: диагональ квадрата делит его на два равных треугольника.

А сейчас давайте посмотрим на изображение храма Парфенон в Афинах.

Даже сейчас, когда он стоит в развалинах, – это одно из самых знаменитых сооружений в мире. Храм был построен в эпоху расцвета древнегреческой математики. И его красота основана на математических законах.

Если мы опишем около фасада Парфенона прямоугольник, то окажется, что его длина больше ширины примерно в 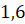раза.

Такой прямоугольник называют золотым прямоугольником. Вычислить точное значение нельзя. Греки умели строить золотые прямоугольники, но не умели находить длины их сторон.

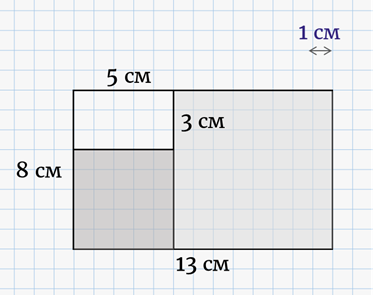
Отличительной особенностью такой фигуры является то, что после удаления квадрата оставшаяся часть остаётся золотым прямоугольником. Проверим это. Вырежем из бумаги прямоугольник со сторонами 13 см и 8 см. Его длина больше ширины примерно в 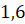раза. Убедитесь в этом самостоятельно.

Отрежем от этого прямоугольника квадрат со стороной 8 см. Тогда у нас останется прямоугольник со сторонами 5 см и 8 см. У него также одна сторона больше другой в 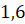раза. Затем от этого прямоугольника отрежем квадрат со стороной 5 см. Останется прямоугольник со сторонами 5 см и 3 см. У этого прямоугольника снова одна сторона больше другой примерно в раза.

Этот процесс можно продолжать и дальше.

На прямоугольники, в которых стороны относятся как 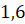к 1, обратили внимание очень давно.

Говорят, что стороны золотого прямоугольника образуют золотое сечение. Слово «сечение» здесь употреблено в смысле «деление на части».

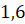
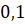
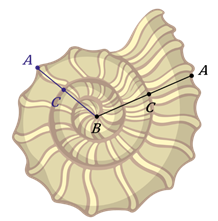
Математики дают точное определение золотому сечению. Золотое сечение – это такое деление целого на две неравные части, при котором большая часть относится к целому как меньшая к большей. Число лишь приближённо (с точностью до ) представляет величину золотого сечения.

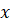
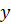
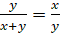
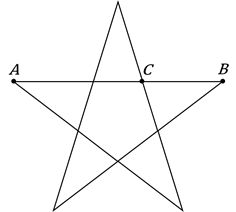
Если отрезок разделён на две части так, что меньшая часть имеет длину , а большая часть имеет длину , то в случае золотого сечения длина большей части отрезка относится к длине всего отрезка как длина меньшей части отрезка относится к длине большей части отрезка ().

В правильной пятиконечной звезде каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения.

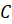
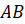
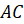
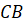
Точка делит отрезок на два отрезка – и .

Тогда

На следующем рисунке изображена раковина. Точка 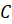делит отрезок приблизительно в отношении золотого сечения.

Золотое сечение очень часто использовалось в архитектуре. В природе золотое сечение тоже не редкость. Линия глаз, на которой человек привык концентрировать своё внимание, слушая собеседника, делит длину лица в отношении золотого сечения.

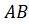
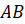
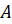
Сейчас давайте с вами построим золотой прямоугольник. Для этого возьмём квадрат и разделим его на два равных прямоугольника. Затем проведём диагональ одного из прямоугольников. Обозначим её. Теперь проведём дугу окружности радиусом и с центром в точке .

Далее продлим основание квадрата до пересечения с этой дугой. Проведём боковую сторону под прямым углом и закончим построение золотого прямоугольника.

Источник