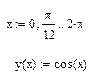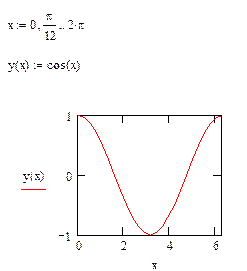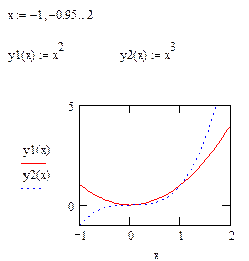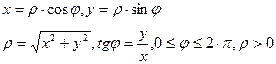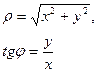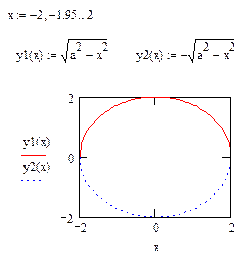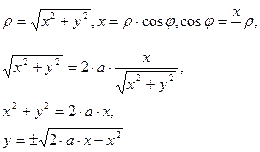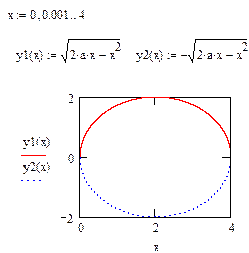Как построить параболу в маткаде

Построение графиков в MathCad

В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:

Построение графика по точкам

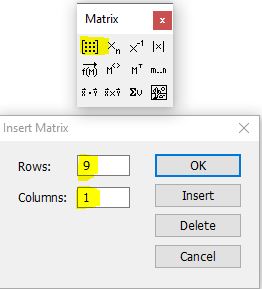
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)

Рис. 1. Создание матриц-столбцов

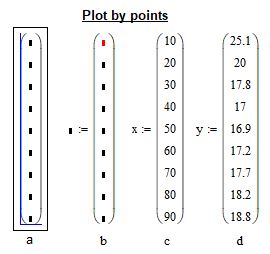
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.

Рис. 2. Заполнение матриц-столбцов для графика

На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)

Рис. 3. Создание заготовки для графика

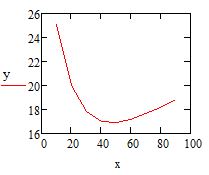
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)

Рис. 4. График по точкам

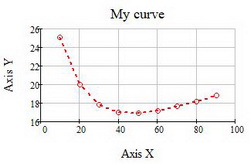
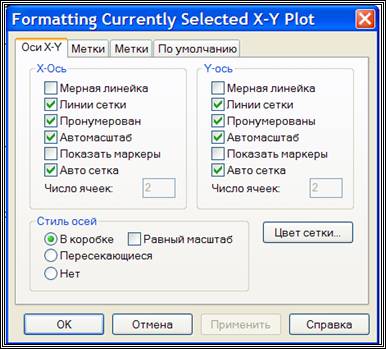
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)

Рис. 5. Настройка отображения графика

Построение графика функции f(x)

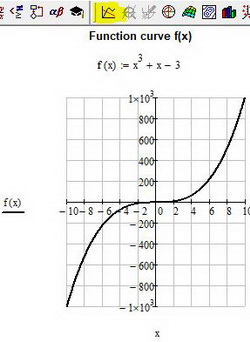
Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой

Рис. 6. Построение графика функции f(x)

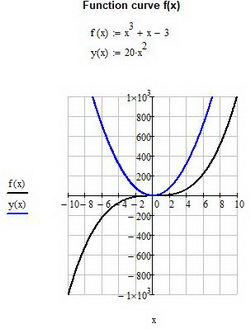
Рис. 7. Построение двух графиков функции

Построение эпюры в mathcad

Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:

— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании

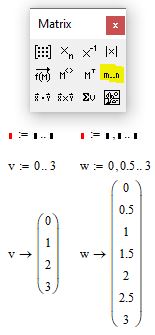
Рис. 8. Ввод ранжированной переменной

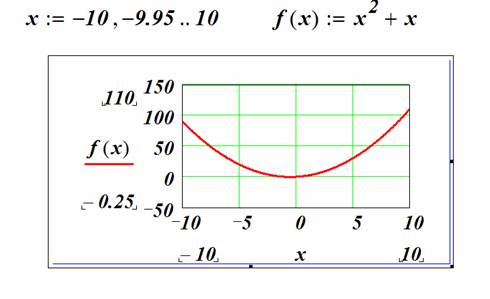
Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже

Рис. 9. Ввод ранжированной переменной

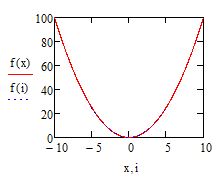
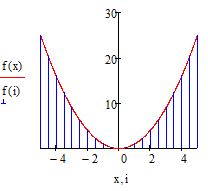
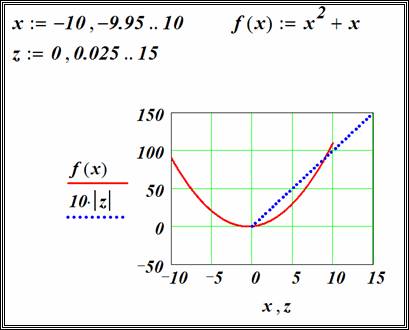
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже

Рис. 10. Построение эпюры. Шаг 1

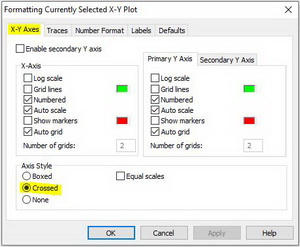
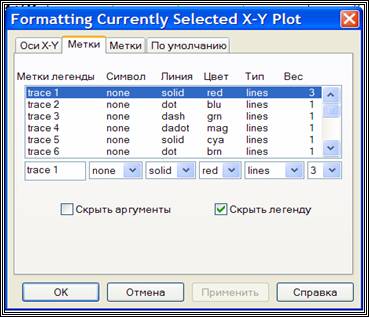
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.

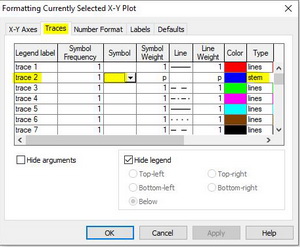
Рис. 11. Построение эпюры. Шаг 2

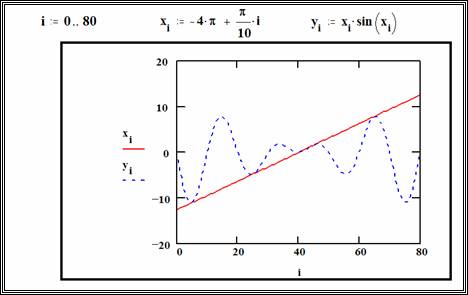
В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)

Рис. 12. Построение эпюры. Шаг 3

Построение графика в полярных координатах в mathcad

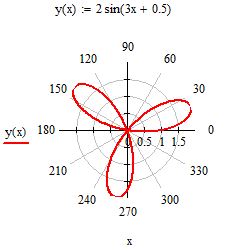
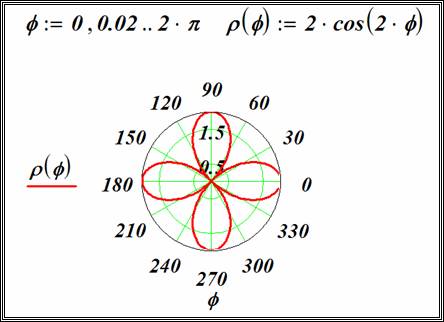
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)

Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph

Рис. 13. Создание загатовки для графика в полярных координатах

Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.

Рис. 14. Построение графика в полярной системе координат

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Источник

Урок 9. 3D-графики функций в Mathcad

Графики двух переменных в PTC Mathcad схожи с 2D-графиками. Однако существуют различия, о которых следует знать. В PTC Mathcad есть два типа 3D-графиков:

Контурный график

Контурный график отражает изменение поверхности по высоте. Он представляет собой линий равных высот. Чтобы вставить контурный график, выберите Графики –> Кривые –> Вставить график –> Контурный график:

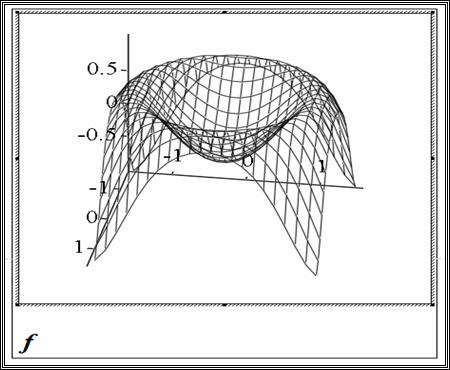
Построим график параболоида:

Функция имеет минимум в начале координат и возрастает при увеличении расстояния от начала координат. Цвет графика зависит от величины функции z:

Попробуйте использовать кнопки для управления видом графика в левом верхнем углу, потом нажмите «Сброс вида».

Щелкните по оси Z на кнопке выбора оси. Измените значение последней (верхней) метки с 200 на 400, затем щелкните по пустой области, чтобы посмотреть, что получилось. Если нужно изменить значение обратно на 200, то нужно сделать это вручную – кнопка сброса вида здесь не сработает.

На втором графике мы изменили цвет графика и добавили заливку поверхности. Попробуйте сделать это с помощью меню Графики –>Стили:

Две функции

Чтобы добавить график второй функции, поместите курсор на местозаполнитель с легендой и нажмите Графики –> Кривые –> Добавить кривую. Ниже мы построили графики параболоида и плоскости:

Для графиков выбрали контрастные цвета, чтобы можно было увидеть их пересечение. Повращайте график, чтобы изучить форму этого пересечения.

Использование вектора

Мы строили 2D-графики с помощью векторов. Нечто похожее можно проделать для 3D-графиков, но нужен вектор со значениями по осям X, Y и Z. Мы показали это на примере функции, известной под названием «Мексиканская шляпа»:

Сфера

Построить параметрическую поверхность несколько сложнее, чем 2D-график, так как Вы можете добавить лишь значение Z на график. Мы проиллюстрируем, как это сделать на примере построения графика сферы с помощью функции CreateMesh. Параметрические уравнения сферы:

Матрица для построения поверхности формируется функцией CreateMesh:

Поместите имя переменной-матрицы в местозаполнитель 3D-графика. и щелкните по пустой области, чтобы увидеть результат:

Резюме

Трехмерные графики имеют некоторые существенные отличия от двухмерных графиков, рассмотренных в предыдущих уроках:

Источник

Лекция 3. Построение графиков в программе Mathcad

ПрограммаMathcad позволяет строить графики в декартовых и полярных координатах. Можно строить двумерные и трехмерные графики.

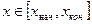
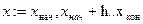
При построении графика сначала должна быть определена независимая переменная. Например, если график строится для всех , тогда необходимо определение независимой переменной:

,

если шаг изменения переменной h. Промежуток изменения переменной можно не задавать, тогда по умолчанию будет строиться график на отрезке 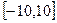. Далее определяется функция, график которой строится.

Пусть необходимо построить график функции

.

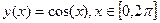
В Mathcad-документе определяются пределы изменения аргумента и сама функция

Если необходимо представить в одном окне два или более графика, то в ячейку рядом с осью ординат вводятся через запятую необходимых имена функций. При этом кривые графиков представляются различным цветом.

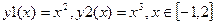
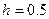
Например, необходимо построить два графика функций с . В Mathcad-документе необходимо выполнить следующие действия.

В программе Mathcad возможно строить графики функций, заданных в полярной системе координат.

В случае, когда начало декартовой системы, совмещено с полюсом, а полярная ось с 0х, то координаты точки 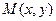связаны с полярными формулами:

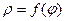
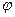
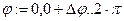
Если функция, график которой следует построить, задана полярным уравнением, т.е. , необходимо в Mathcad-документе определить переменную, задающую границы изменения полярного угла :

.

Задать функцию пользователя

.

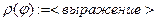
Для ввода греческих букв используется панель Greek(меню View, подменю Toolbars).

.

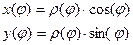
можно записать уравнение, заданное в полярных координатах, в декартовых координатах.

Пример 1.

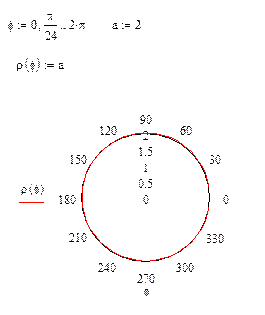
Уравнение 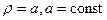определяет уравнение окружности в полярной системе координат.

Уравнение в декартовой системе для этой окружности можно записать;

.

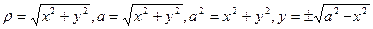
Если построить график в декартовой системе координат, то получим окружность с центром в начале координат.

Пример 2.

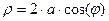
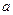
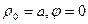
Задано уравнение . Это уравнение окружности радиуса , центр которой находится в точке .можно записать данное уравнение окружности в декартовых координатах. Для этого будем использовать формулы

В полярных координатах график будет иметь вид

Лекция 4.

Mathcad имеются мощные возможности выполнения операций с векторами и матрицами. При этом операции можно производить как символами, так и численно.

Дата добавления: 2015-12-26 ; просмотров: 7747 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Построение графиков в пакете Mathсad

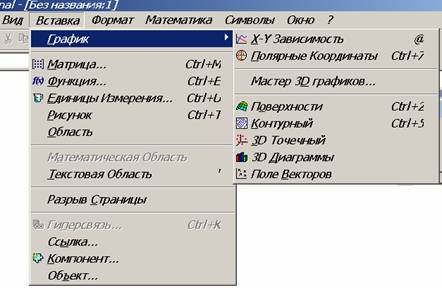
Для построения обратиться к пункту ВСТАВКА команда ГРАФИК (см. рисунок)

Построение графиков функций одной переменной

· щелкнуть мышью в том месте, где нужно создать график;

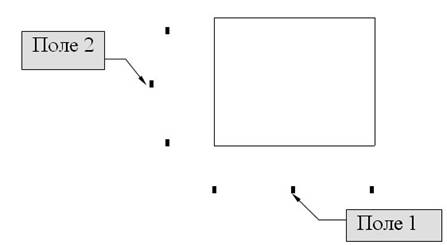
· обратиться к пункту Вставка, командам График – Х-У Зависимость. В рабочем документе создается пустой график с шестью полями ввода;

Другие четыре поля используются для выбора границ на осях координат

Форматирование и редактирование графиков

Для изменения формата осей, способа их оцифровки, цвета графиков необходимо:

· щелкнуть мышью на графике, чтобы он заключился в синюю рамку;

· обратиться к появившемуся пункту X-Y-Plot, команде Format;

· используя закладки X-Y-оси, Графики, надписи выполнить форматирование

Построение нескольких графиков

Графическое представление вектора

Графики в полярной системе координат

График параметрической функции

Графики функций двух переменных (поверхностей)

Для создания трехмерного графика (графика функции двух переменных) необходимо щелкнуть на одной из следующих кнопок палитры Графика с изображением требуемого типа графика. В документе появится шаблон графика с тремя осями и пустым полем. В это поле вводится либо имя массива, либо имя функции двух переменных.

В первом случае предварительно необходимо сформировать матрицу из значений функции в узлах прямоугольной сетке.

Во втором случае предварительно надо описать функцию от двух переменных.

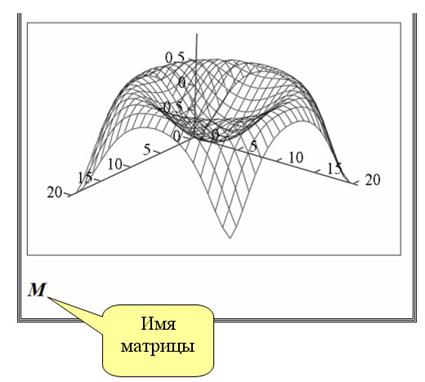
Пример построения графика с формированием матрицы. Необходимо построить график функции

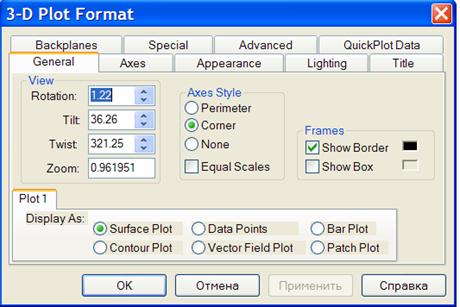
Окно форматирования трехмерных графиков вызывается аналогично и имеет ряд вкладок:

· общие – установка общих параметров форматирования;

· ось – установка параметров форматирования координатных осей;

· вид – установка вида графика;

· освещение – задание условий освещения и выбор схемы освещения;

· название – задание титульных надписей и их параметров;

· основание – установка параметров форматирования граней;

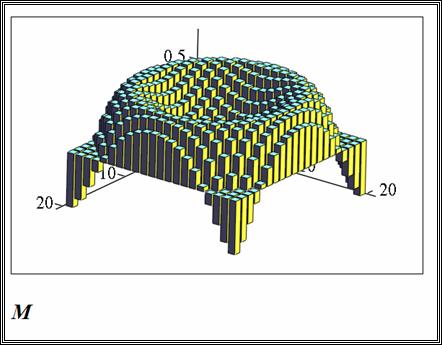
· особый – задание специальных эффектов форматирования;

· дополнительно – установка дополнительных параметров;

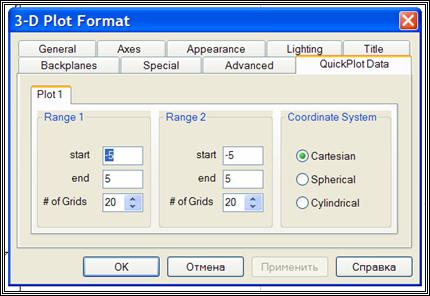
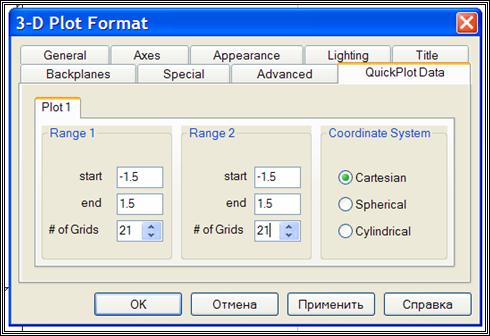
· данные QuickPlot – параметры быстрого построения графика.

Автоматическое формирование матрицы

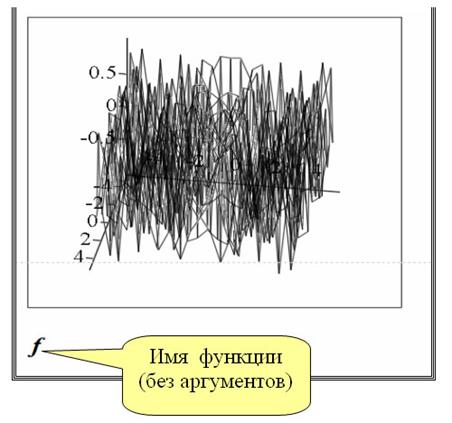
Графики векторных полей

Для отрисовки векторного поля ( в каждой точке такого поля задается не скалярная величина, а вектор с двумя проекциями ) необходимо :

· вычислить две матрицы ( первая содержит проекции вектора на ось Х, вторая на ось У ) или сформировать комплексную матрицу;

· заполнить в нижней части появившегося шаблона поле, введя туда имена двух вещественных массивов или имя одного комплексного массива.

Источник