Как построить ось симметрии прямой

Осевая симметрия

Осевая симметрия — это симметрия относительно прямой.

Пусть дана некоторая прямая g.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

1) Провести из точки A к прямой g перпендикуляр AO.

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

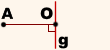
Полученная точка A1 симметрична точке A относительно прямой g.

Прямая g называется осью симметрии.

Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.

Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.

Преобразование фигуры F в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.

Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.

Примеры фигур, симметричных относительно прямой.

1) Прямоугольник.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

Ромб имеет две оси симметрии:

прямые, на которых лежат его диагонали.

3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

Окружность имеет бесконечное множество осей симметрии:

любая прямая, содержащая диаметр, является осью симметрии окружности.

Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.

Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.

Равнобедренный треугольник имеет одну ось симметрии:

прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

8) Равносторонний треугольник.

Равносторонний треугольник имеет три оси симметрии:

прямые, содержащие его высоты (медианы, биссектрисы).

Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

Осевая симметрия является движением.

Источник

Осевая и центральная симметрия

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

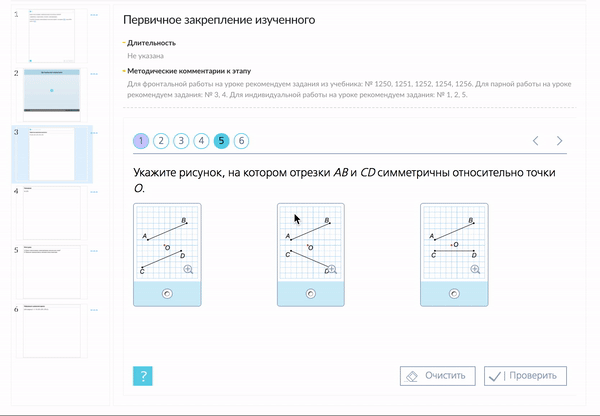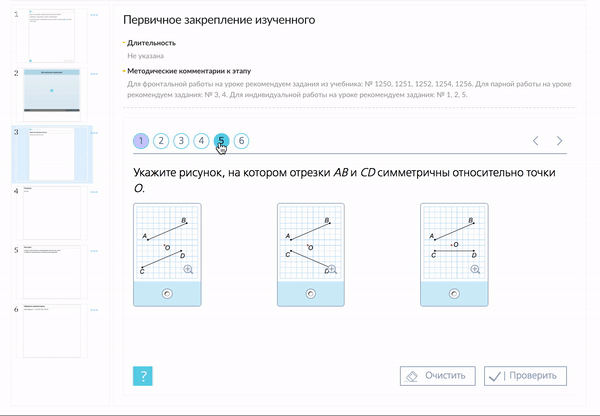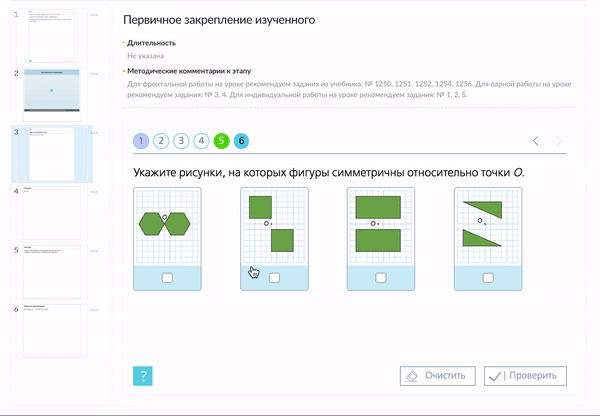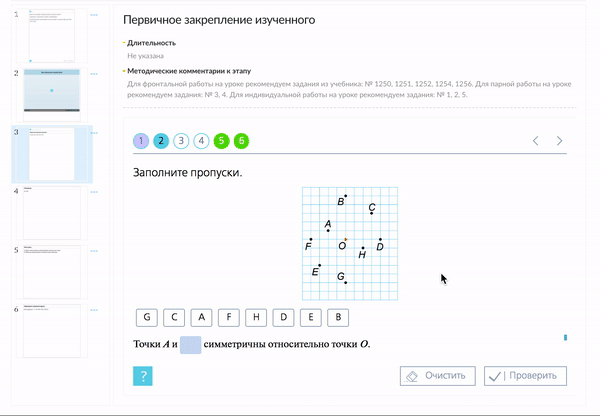
Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Геометрия. 8 класс

Конспект
Рассмотрим прямую a и точку, не принадлежащую ей.

Точки А и А₁ называются симметричными относительно прямой а, если:
— эта прямая проходит через середину отрезка АА₁
— а ⊥ АА₁.
Прямая a называется осью симметрии. Если точка принадлежит прямой а, то она симметрична сама себе.
Составим алгоритм построения точки, симметричной данной.
Алгоритм построения
• Провести прямую b перпендикулярную прямой а
• Отложить от точки О на прямой b расстояние, равное ОА
• Получить точку А₁

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.

(Цвет линий и букв черный)
Равносторонний треугольник имеет три оси симметрии. Неразвернутый угол имеет одну ось симметрии – прямую, содержащую биссектрису угла.

Подумайте, какие из данных фигур имеют ось симметрии и сколько?
Рассмотрим симметрию относительно точки.
Симметрия относительно точки
Две точки А и А₁ называются симметричными относительно точки О, если О – середина отрезка АА₁.

Составим алгоритм построения точки, симметричной данной относительно точки О.
Алгоритм построения
• Соединить точку А и точку О прямой и продолжить прямую за точку О
• От точки О отложить расстояние равное ОА
• Получить точку А₁

Фигура называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

Центр симметрии имеет круг, квадрат.

Подумайте, какие из данных фигур имеют центр симметрии?

Слово «симметрия» греческое (συμμετρία), оно означает «соразмерность, пропорциональность, одинаковость в расположении частей», неизменность при каких-либо преобразованиях.
В словаре С.И. Ожегова симметрия – это соразмерность, пропорциональность частей чего-нибудь, расположенных по обе стороны от середины, центра.
С симметрией мы часто встречаемся в природе, архитектуре, искусстве, технике и быту. Симметрия в одежде – это символ строгости. Симметрия в архитектуре – это признак красоты и надежности. Некоторые люди утверждают, что симметрия – это совершенство.
Симметрией обладают некоторые буквы латинского и русского алфавита. Например, буква М обладает осевой симметрией, а буква Х – центральной симметрией.
Многие дорожные знаки обладают осевой или центральной симметрией. Гуляя по городу, приглядитесь к знакам. Найдите такие, которые имеют несколько осей симметрии и такие, которые не имеют осей симметрии.

Есть ось симметрии, центра симметрии нет Есть центр симметрии и 4 оси симметрии
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Источник

Осевая и центральная симметрии. Проводим урок с ЭФУ

Повторение материала

Из курса математики 5 класса учащиеся уже узнали, как выглядят и строятся фигуры, имеющие ось симметрии. Перед изучением темы «Осевая и центральная симметрии» будет целесообразно повторить материал 5 класса. Следует разъяснить учащимся, что построение фигуры во многих случаях возможно по положению ключевых точек.

Для закрепления этого интуитивно-наглядного понимания, учитель может предложить детям перегнуть лист бумаги, на котором изображены симметричные фигуры.

.

Понятие симметрии

Слово «симметрия» происходит от греческого symmetria, что означает соразмерность. В нашем случае, симметрия — это свойство геометрических фигур к отображению.

Учитель: Симметрия используется в рисунках, орнаментах, архитектуре с давних времен. Где еще симметрию могут использовать люди?
Ученики: при строительстве домов; в изготовлении предметов быта.
Учитель: верно, но ведь симметрия распространена не только там, где творил человек! Мы видим симметричные объекты природы каждый день. Назовите мне три таких объекта!
Ученики: Бабочка, цветы, форма листа! Морская звезда, снежинка, яблоко в разрезе.

Симметрий, как это не покажется вам странным и любопытным, много, но мы будем рассматривать две симметрии на плоскости: относительно точки и прямой.

Осевая симметрия

Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Заметим, что любые две фигуры, симметричные относительно некоторой прямой, равны (Рис.131). Все точки фигуры, имеющей ось симметрии, не принадлежащие этой оси, можно разделить на пары симметричных точек (Рис. 132).

Центральная симметрия

Симметрию относительно точки называют центральной симметрией.

Фигуры, имеющие центр симметрии — понятие, воспринимающееся учащимися сложнее, чем фигуры, имеющие ось симметрии. Для удобства восприятия и понимания, рекомендуется привести как можно больше примеров из окружающей природы.

В зависимости от уровня математической подготовки учащихся класса, можно обратить их внимание на то, что прямая — это фигура, имеющая бесконечно много осей и центров симметрии.

С помощью заданий из «Классной работы» материал можно закрепить в различных графических форматах.

Актуализация знаний

Предложите ребятам решить задание № 1260. Какие печатные буквы русского алфавита имеют 1) вертикальную ось симметрии; 2) горизонтальную ось симметрии; 3) горизонтальную и вертикальную оси?

Готовый яркий раздаточный материал «Алфавит» вы можете скачать в конце этой статьи.

Также рекомендуем вам применять на уроке различные методы преподнесения информации: как визуальный, так и аудио. Попробуйте аудиодиктант.

Источник

Класс: 6

Презентация к уроку

Аннотация

Уроки в школе – это значительная часть жизни школьников, требующая элементарного комфорта, благоприятного общения. Эффективность учебного процесса зависит не только от способностей прилежания и трудолюбия учеников, наличия целенаправленной мотивации учителя, но и от формы проведения уроков.

Использование информационных технологий позволяет экономить время при объяснении нового материала, представлять материал в наглядном, доступном для восприятия виде, воздействовать на разные системы восприятия учащихся, обеспечивая тем самым лучшее усвоение материала.

Большое внимание уделяется применению полученных знаний по математике в повседневной жизни. Знакомство с красотой в жизни и искусстве не только воспитывает ум и чувство ребёнка, но и способствует развитию воображения и фантазии. Я считаю, что урок с элементами творческой деятельности помогает активизировать мыслительную деятельность школьников и поэтому проходит на высоком эмоциональном уровне, что позволяет рассмотреть большое количество теоретических вопросов и задач, привлечь к работе всех учащихся класса. С целью повышения активности учащихся на протяжении всего урока используется чередование видов деятельности.

На завершающем этапе урока ученики выполняют проверочную работу в виде теста, проводят самопроверку, оценивая свою работу по заданным критериям. Наиболее активной группе учащихся предложен дополнительный материал по изученным темам.

Рефлексия в конце урока помогает определить уровень усвоения материала и поставить цели для дальнейшей работы.

Домашнее задание состоит из двух частей, что позволяет не только продолжить закрепление полученных знаний, но развивать творческие способности детей.

На мой взгляд, такие уроки дают возможность учителю творить, искать, работать на высокие результаты, формировать у учеников универсальные учебные действия – таким образом, готовить их к продолжению образования и к жизни в постоянно изменяющихся условиях.

Тип урока: урок «открытия» нового знания.

Оборудование: компьютер, булавка или циркуль, проектор, карточки, геометрические фигуры из бумаги.

1. Оргмомент

(Слайд 1) Легко отыскать примеры прекрасного, но как трудно объяснить, почему они прекрасны. (Платон )

– Сегодня на уроке мы попытаемся разобраться в некоторых особенностях создания прекрасного.

2. Актуализация

– Посмотрите на кленовый лист, снежинку, бабочку. (Слайд 2) Что их объединяет, что у них общего? То, что они симметричны.
– Напомните мне, пожалуйста, что же означает слово «симметрия».
– «Симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». Если поставить зеркальце вдоль прочерченной на каждом рисунке прямой, то отраженная на зеркале половинка фигуры дополнит ее до целой. Потому такая симметрия называется зеркальной (осевой).

(Учитель показывает опыт на елочке вырезанной из цветной бумаги)

– Прямая, вдоль которой поставлено зеркало, называется осью симметрии. Если согнуть лист по этой прямой, то эти фигуры полностью совпадут, и мы сможем видеть только одну фигуру. Как вы думаете, какова тема сегодняшнего урока? (Осевая симметрия)

– Ребята, сегодня мы научимся строить фигуры симметричные относительно прямой, а также вы узнаете, где применяется осевая симметрия.
– А как же получить симметричные фигуры?
– Для начала рассмотрим самый простой способ получения симметричных фигур.
У каждого из вас на столе лист белой бумаги. Возьмите лист бумаги и перегните его пополам. Теперь на одной стороне постройте треугольник (1 ряд – остроугольный, 2 ряд – прямоугольный, 3 ряд – тупоугольный).
Далее проколите вершины данной фигуры так, чтобы были проколоты обе половинки. Теперь разверните лист и соедините по линейке полученные точки-дырочки. Таким образом, мы с вами построили фигуры, симметричные данным относительно прямой (линии перегиба). Убедитесь в этом. Для этого сложите лист по линии сгиба и посмотрите через него на свет.
– Что вы видите? (Фигуры совпали.)
– Это самый простой способ построения симметричных фигур.
– Но всегда ли на практике, таким образом, мы сможем построить симметричные фигуры?
– А что мы сделали для того, что бы построить симметричные треугольники?
– Перегнули лист пополам.
– Т.е. провели ось симметрии. Дальше.
– Прокололи вершины треугольника.
– Т.е. построили точки, которыми ограничен наш треугольник.
– А это значит, что прежде чем построить фигуру симметричную данной мы должны научится строить в первую очередь что? (Точку симметричную данной.)
– Как это можно сделать, давайте разберемся.

3. Сейчас выполним практическую работу:

– Отметьте точку Аа. Из точки А опустите перпендикуляр АО на прямую а. Теперь от точки О отложите перпендикуляр ОА1= АО. Две точки А и А1 называются симметричными относительно прямой а. Такая прямая называется осью симметрии.

(Учитель строит на доске, ученики в тетрадях).

– Какие две точки называются симметричными относительно прямой?
– А как построить фигуру симметричную относительно некоторой прямой?
– Давайте попробуем построить треугольник симметричный относительно прямой.

(Учитель вызывает к доске желающего ученика, остальные работают в тетрадях).

После проделанной работы ученики делают вывод вместе с учителем.

Вывод: Чтобы построить геометрическую фигуру, симметричную данной относительно некоторой прямой, надо построить точки, симметричные значимым точкам (вершинам) данной фигуры относительно этой прямой и потом соединить эти точки отрезками.

– Ребята, симметричными могут быть не только 2 фигуры, в некоторых фигурах тоже можно провести ось симметрии. Говорят, что такие фигуры обладают осевой симметрией. Назовите фигуры, обладающие осевой симметрией.

(Учитель называет и показывает геометрические фигуры, вырезанные из цветной бумаги)

– А как вы думаете, сколько осей симметрии у равнобедренного треугольника, прямоугольника, квадрата? (Прямоугольник имеет 2 оси симметрии. Квадрат имеет 4 оси симметрии) – А у круга? (Круг имеет бесконечно много осей симметрии).

– Назовите фигуры, которые не имеют оси симметрии. (Параллелограмм, разносторонний треугольник, неправильный многоугольник).

– Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Симметрично практически все транспортные средства, предметы домашнего обихода (мебель, посуда), некоторые музыкальные инструменты.
– Приведите примеры предметов имеющих осевую симметрию.

– Законы природы, управляющие неисчерпаемой в своем многообразии картиной явлении, в свою очередь, также подчиняются принципам симметрии. Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.

Симметрия часто встречается в предметах созданных человеком.
Симметрия встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.

Впечатляющие результаты дает симметрия в изобразительном искусстве. (Слайды 20-21)
Художники эпохи Возрождения часто использовали язык симметрии в построении своих композиций. Это следовало из их логики понимания картины как изображения идеального мироустройства, где царит разумная организованность и уравновешенность, которые человек может познать и осмыслить.
В удивительной картине «Обручение девы Марии» великий Рафаэль воспроизвел такой образ мира, существующего по законам гармонии и строгой логики. Использованный принцип симметрии создает впечатление покоя и торжественности и в то же время некой отстраненности от зрителя. Вход в изящную ротонду и кольцо, одеваемое Иосифом на руку Марии, совпадают с центральной осью симметрии картины.
В работе Леонардо «Тайная вечеря» преобладают строгие построения перспективы интерьера. Композиционное развитие здесь базируется на зеркальном повторе правой и левой частей. Конечно, чаще всего в изобразительном искусстве мы говорим о неполной симметрии.
В картине «Три богатыря» русского художника В. Васнецова сами герои полны сдерживаемой силы. Из-за этих небольших отклонений от строгой симметричности возникает ощущение внутренней свободы персонажей, их готовности к движению.
Буквы русского языка тоже можно рассмотреть с точки зрения симметрии. (Слайды 22-23)
Весь алфавит разделен на 4 группы, как вы думаете, по каким критериям я это сделала?
Буквы А, М, Т, Ш, П имеют вертикальную ось симметрии, В, З, К, С, Э, В, Е – горизонтальную. А буквы Ж, Н, О, Ф, Х имеют по две оси симметрии.
Симметрию можно увидеть и в словах: казак, шалаш. Есть и целые фразы с таким свойством (если не учитывать пробелы между словами): “Искать такси”, “Аргентина манит негра”, “Ценит негра аргентинец”. Такие слова называются палиндромами. Ими увлекались многие поэты.
Рассмотрим примеры слов, имеющих горизонтальную ось симметрии:
СНЕЖОК, ЗВОНОК, КОНЕК, НОС
Слова, имеющие вертикальную ось симметрии:

Х	Т
О	О
Л	П
О	О
Д	Т

Некоторые композиторы, в том числе и великий Бах, писали музыкальные палиндромы.

(Слайд 24) Те, кому повезло иметь симметричное лицо, вероятно, уже заметили, что пользуются успехом у противоположного пола. Также это может свидетельствовать об их хорошем здоровье. Дело в том, что лицо с идеальными пропорциями является признаком того, что организм его обладателя хорошо подготовлен для борьбы с инфекциями. Обычная простуда, астма и грипп с высокой вероятностью отступают перед людьми, у которых левая сторона в точности похожа на правую.

Физкультминутка (Слайд 25)

Раз – подняться, потянуться,
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
Головою тори кивка.
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту сесть опять.

Проводится тест с последующей самопроверкой.

– Не забудем про гимнастику ума. Примеры у нас сегодня тоже симметричные. Кто уже выполнил задание, можете посчитать устно вот эти симметричные примеры. (Слайд 30)

Вариант 1 Вариант 2

1) Б 2) Г 3) Б 4) А 5) В 1) В 2) Б 3) Б 4) Г 5) Г

Оценивание выполненной работы по соответствующим критериям:

«5» – 5 заданий;
«4» – 4 задания;
«3» – 3 задания;
«2» – менее трёх заданий.

– Попробуйте ответить на вопрос какая фигура лишняя и почему? (Слайд 31)

(Фигура № 3, т.к не имеет ось симметрии)

5. Итог урока. Рефлексия

– Подходит к концу наш урок, но знакомство с симметрией продолжается. На протяжении всего урока мы выполняли разнообразные задания.
– С каким понятием вы сегодня познакомились?
– Какие цели мы ставили на урок? Мы выполнили поставленные цели? Кто же лучше всех трудился? Кто на уроке отличился? Какое задание вам показалось самым трудным? Какой теоретический материал помог справиться с заданием?
– Какое задание вам показалось самым интересным? Что нового «открыли» вы для себя на уроке? Как вы думаете, над чем, каждому из вас следует потрудиться?

– Ребята, спасибо вам за работу! Без помощи и поддержке друг друга мы не смогли бы достичь цели. Я очень довольна вашей работой на уроке. Считаете ли вы, что мы не напрасно провели эти минуты вместе? Поделитесь своими впечатлениями о нашем уроке.

7. Заключение

Действительно симметричные объекты окружают нас буквально со всех сторон, мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Симметрия противостоит хаосу, беспорядку. Получается, что симметрия – это уравновешенность, упорядоченность, красота, совершенство.
Весь мир можно рассмотреть как проявление единства симметрии и асимметрии. Симметрия многообразна, вездесуща. Она создает красоту и гармонию.
И на вопрос: “Есть ли будущее без симметрии?” мы можем ответить словами классика современного естествознания, мыслителя Владимира Ивановича Вернадского “Принцип симметрии охватывает все новые и новые области…”

Источник