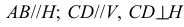Как построить окружность в плоскости

Как построить окружность в плоскости

§ 14. Построение аксонометрических проекций окружности

Рассмотрите рис. 92. На нем дана фронтальная диметрическая проекция куба с вписанными в его грани окружностями.

Рис. 92. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Окружности, расположенные на плоскостях, перпендикулярных к осям х и z, изображаются эллипсами. Передняя грань куба, перпендикулярная к оси у, проецируется без искажения, и окружность, расположенная на ней, изображается без искажения, т. е. описывается циркулем. Поэтому фронтальная диметрическая проекция удобна для изображения предметов с криволинейными очертаниями, подооных представленными на рис. 93.

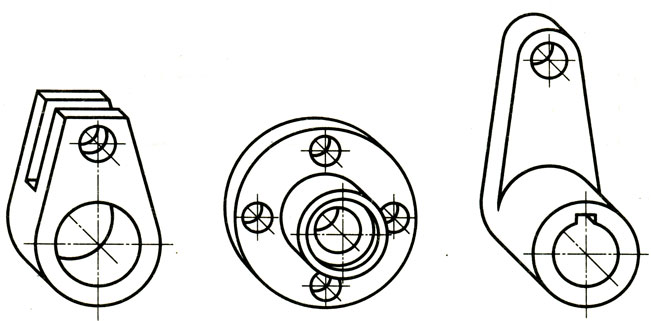
Рис. 93. Фронтальные диметрические проекции деталей

Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием. Фронтальную диметрическую проекцию плоской детали с цилиндрическим отверстием выполняют следующим образом.

1. Строят очертания передней грани детали, пользуясь циркулем (рис. 94, а).

2. Через центры окружности и дуг параллельно оси у проводят прямые, на которых откладывают половину толщины детали. Получают центры окружности и дуг, расположенных на задней поверхности детали (рис. 94, б). Из этих центров проводят окружность и дуги, радиусы которых должны быть равны радиусам окружности и дуг передней грани.

Рис. 94. Построение фронтальной диметрической проекции детали с цилиндрическими элементами

3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 94, в).

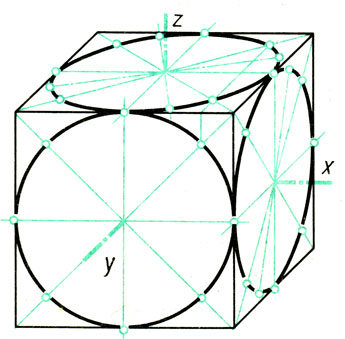
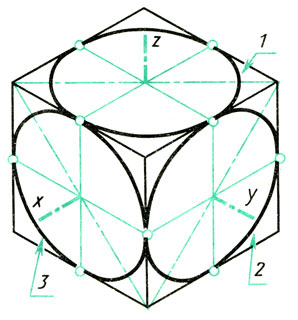
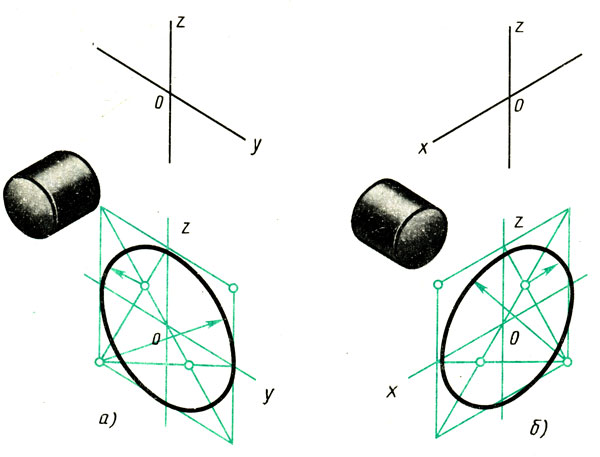
Изометрические проекции окружностей. Квадрат в изометрической проекции проецируется в ромб. Окружности, вписанные в квадраты, например, расположенные на гранях куба (рис. 95), в изометрической проекции изображаются эллипсами. На практике эллипсы заменяют овалами, которые вычерчивают четырьмя дугами окружностей.

Рис. 95. Изометрические проекции окружностей, вписанных в грани куба

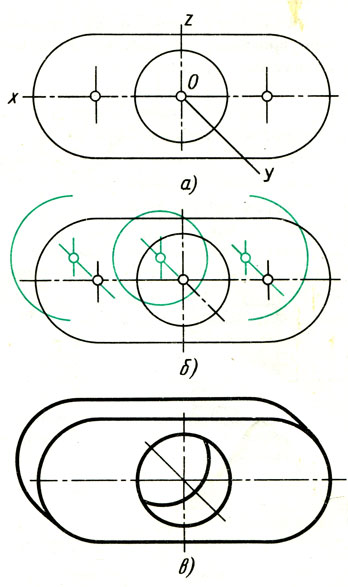
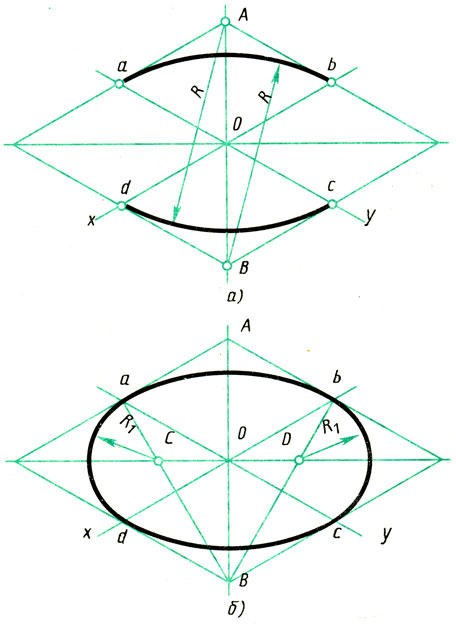
Построение овала, вписанного в ромб.

1. Строят ромб со стороной, равной диаметру изображаемой окружности (рис. 96, а). Для этого через точку О проводят изометрические оси х и у и на них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, w, с и d проводят прямые, параллельные осям; получают ромб. Большая ось овала располагается на большой диагонали ромба.

Рис. 96. Построение овала в плоскости, перпендикулярной оси z

Рис. 97. Построение овала в плоскостях, перпендикулярных осям х и у

Построение изометрической проекции детали с цилиндрическим отверстием.

Как применить рассмотренные построения на практике?

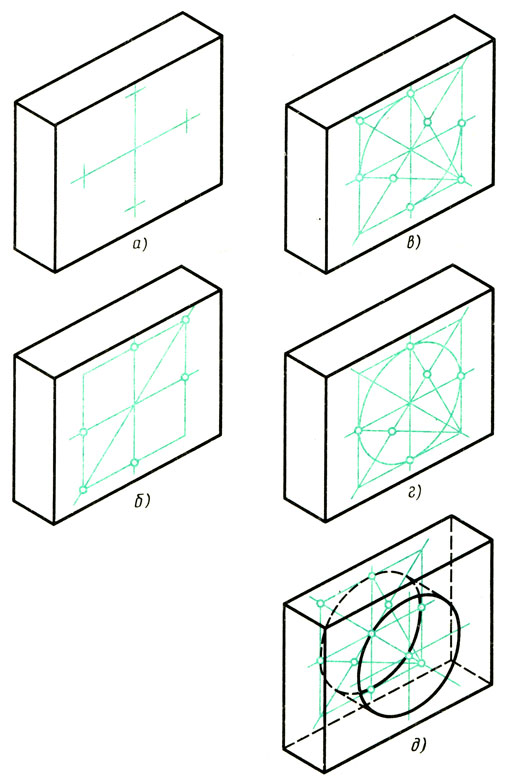
Дана изометрическая проекция детали (рис. 98, а). Нужно изобразить сквозное цилиндрическое отверстие, просверленное перпендикулярно передней грани.

Построения выполняет следующим образом.

1. Находят положение центра отверстия на передней грани детали. Через найденный центр проводят изометрические оси. (Для определения их направления удобно воспользоваться изображением куба на рис. 95.) На осях от центра откладывают отрезки, равные радиусу изображаемой окружности (рис. 98, а).

2. Строят ромб, сторона которого равна диаметру изображаемой окружности; проводят большую диагональ ромба (рис. 98, б).

3. Описывают большие дуги овала; находят центры для малых дуг (рис. 98, в).

4. Проводят малые дуги (рис. 98, г).

5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 98, д).

Рис. 98. Построение изометрической проекции летали с цилиндрическим отверстием

Ответьте на вопросы

1. Какими фигурами изображаются во фронтальной диме-трической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х и у?

2. Искажается ли во фронтальной диметрической проекции окружность, если ее плоскость перпендикулярна оси у?

4. Какими фигурами изображаются в изометрической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х, у, z?

5. Какими фигурами в практике заменяют эллипсы, изображающие окружности в изометрической проекции?

6. Из каких элементов состоит овал?

7. Чему равны диаметры окружностей, изображенных овалами, вписанными в ромбы на рис. 95, если стороны этих ромбов равны 40 мм?

Задания к § 13 и 14

Упражнение 42

Рис. 99. Задание для упражнений

Упражнение 43

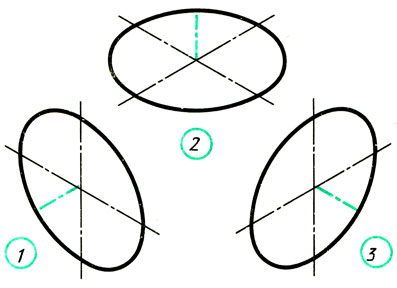
Запишите, какой оси (х, у или z) перпендикулярны плоскости овала на рис. 100. В какой аксонометрической проекции даны здесь окружности?

Рис. 100. Задание для упражнений

Упражнение 44

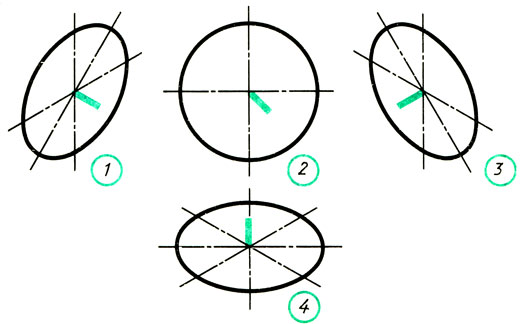
В каких аксонометрических проекциях даны окружности на рис. 101? Какой оси перпендикулярна плоскость каждой из них?

Рис. 101. Задание для упражнений

Упражнение 45

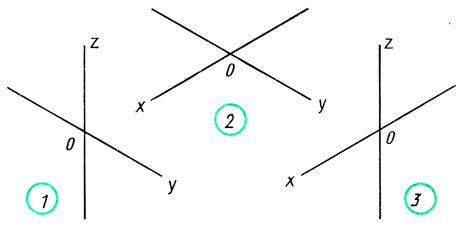
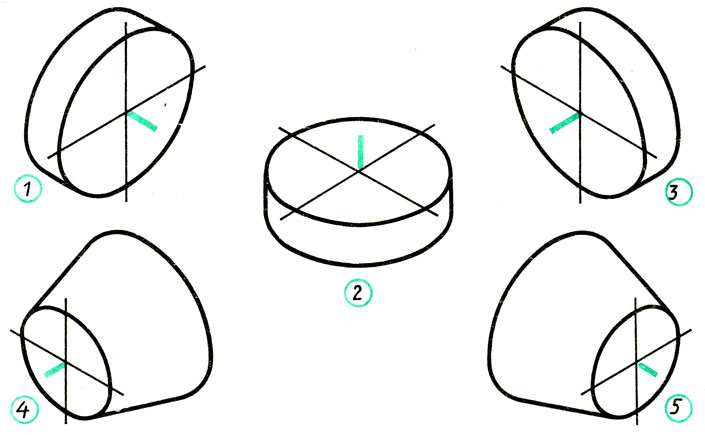
Запишите, в каких аксонометрических проекциях даны геометрические тела на рис. 102.

Каким осям (х, у или z) параллельна высота каждого из них?

Рис. 102. Геометрические тела для задания для упраждений

Упражнение 46

Источник

Построение окружности в начертательной геометрии с примером

Построение окружности:

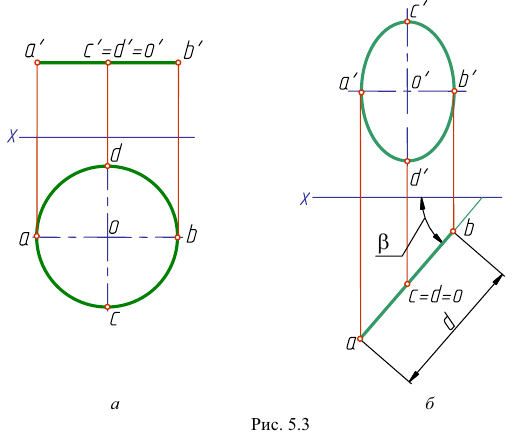
Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров.

Если окружность расположена в плоскости уровня, например в плоскости, параллельной плоскости Н (рис. 5.3, а), то в этом случае фронтальной проекцией окружности служит отрезок, равный d, а гори­ зонтальной проекцией является окружность.

Если окружность расположена в проецирующей плоскости, то проекции ее диаметров параллельны плоскостям проекций. Например,

Если окружность расположена в плоскости общего положения, она проецируется на все плоскости проекций в виде эллипсов, которые можно построить по сопряженным диаметрам. Эти диаметры являются проекциями диаметров, параллельных плоскостям проекций.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

ИЗОБРАЖЕНИЕ ОКРУЖНОСТИ В ПЕРСПЕКТИВЕ.

Перспектива окружности в горизонтальной плоскости.

Множество предметов, находящихся вокруг нас, имеют формы,

очертанием которых является окружность.

Чаще всего эта окружность находится в горизонтальной плоскости: это могут быть края чашки, стоящей на столе или табуретка с круглым сидением.

Если такая окружность находится на уровне наших глаз, на линии горизонта, мы видим ее как прямую линию.

Если мы смотрим на окружность сверху, то мы видим ее без искажений, как окружность.

Во всех остальных случаях, когда окружность располагается в горизонтальной плоскости, мы видим ее как эллипс.*

То есть, как лекальную кривую, симметричную относительно двух взаимно перпендикулярных осей.

При чем, одна из этих осей ВСЕГДА строго вертикальна, а другая, соответственно, горизонтальна.

*Строго говоря, изображение окружности в перспективе не является эллипсом, так как дальняя от нас его часть чуть меньше, чем ближняя. И, соответственно, он не симметричен относительно горизонтальной оси.

Соотношение между длинами осей эллипса называют раскрытием.

Грубо говоря, чем больше эллипс похож на круг, тем более он раскрытый.

В изображении эллипсов в горизонтальной плоскости есть два основных правила:

Упражнение 1.

Постройте окружность тем же способом, с той же точкой схода, но выше линии горизонта. Выделите более толстой линией ее передний край.

ОБРАТИТЕ ВНИМАНИЕ что в рисунке окружности, лежащие в горизонтальной плоскости мы НЕ строим с помощью описанного квадрата. Так как этот даёт искажения, если точка схода для квадрата не лежит на вертикальной оси эллипса.

Мы проводим две оси эллипса и задаем степень раскрытости на глаз, но учитываем положение эллипса относительно линии горизонта и других эллипсов.

Упражнение 2.

На рисунках изображена последовательность построения цилиндра и конуса.

Перспектива окружности в вертикальной или наклонной плоскости.

С окружностями в вертикальной плоскости нам приходится иметь дело достаточно часто. Например, рисуя арки в архитектуре.

Самый простой случай — когда окружность находится в плоскости параллельной картинной. Тогда мы видим ее без искажений.

View of the Tiber with the Castel Sant’Angelo
Bernardo Bellotto1743/1744

В этом курсе мы только знакомимся со способом построения окружности в вертикальной плоскости. Но если у вас есть желание, подробно об этом можно прочитать в учебнике Осмоловской (ст. 26) или, в упрощенном виде у Шарова и Барщ.

Перспективные зарисовки с натуры.

Мы закончили блок теории построений. Теперь начинаем работать с натуры.

На этом этапе важно осознать, что рисунок — не черчение. В рисунке мы не пользуемся линейкой, редко строим точки схода на дополнительном листе. Наша задача, зная, какие построения применялись бы для перспективного чертежа, сделать минимум из них на глаз так, чтобы в результате получилось убедительное изображение, соответствующее основным правилам перспективы.

Рисование с фотографии.

Я вас очень прошу, по крайней мере на начальном этапе не срисовывать с фотографии, даже называя это рисованием с референсов.

Рисуя с фото вы НЕ развиваете пространственное воображение и умение на плоскости изображать объем. Вы только учитесь копировать с одного листа на другой пятна тона. Это, конечно, тоже полезный навык но для хорошего рисунка его не достаточно.

Постановка натуры.

Правильная постановка натуры помогает избежать многих ошибок в рисунке и делает работу легче и приятнее.

Поэтому я очень прошу вас уделить этому внимание.

Рисунок с натуры коробки или книжки.

Упражнение 4

Нарисуйте с натуры предмет с прямыми ребрами ( книжку, коробку и т. п.)

Мы НЕ рисуем с фото, мы НЕ копируем рисунок, разобранный выше.

Упражнение 5

Нарисуйте два предмета с прямыми ребрами, один из которых стоит на другом.

РИСУНОК С НАТУРЫ КРУЖКИ.

Для постановки нужно выбрать кружку простой цилиндрической формы, с ручкой. Саму кружку мы видим без сокращений, поэтому отношение высоты и ширины можно измерить, приложив карандаш непосредственно к натуре.

Упражнение 6

Нарисуйте кружку с натуры.

Упражнение 7.

Нарисуйте ту же кружку в другом ракурсе по представлению(не глядя на натуру)

Источник

Изображение кругов в изометрических и диметрических проекциях

Из геометрии известно, что круг можно рассматривать как правильный многоугольник с большим количеством сторон. Следовательно, изометрическое изображение круга можно строить так же, описывая вокруг него квадрат (рис. 155, а). Точки касания А, В, С и D будут находиться на средине сторон квадрата и легко могут быть нанесены на аксонометрическое изображение (рис. 155, б). Промежуточные точки Е’, F’ и другие находим с помощью их координат. Изометрической проекцией круга является эллипс; его большая ось EG расположена под углом 60° к горизонту по большой диагонали ромба, а малая ось — под углом 30° по малой диагонали ромба.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451018_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Аксонометрические изображения круга чаще строят, проводя оси х и у через центр окружности (рис. 156, а); при этом отпадает надобность в построениях квадрата и ромба. Выбрав точку О’, проводим через нее оси х’ и у’ (рис. 156, б), откладываем на осях величины, равные радиусу окружности, получаем точки А’, В’, С и D’. Другие точки находим с помощью их координат; построение точки Е показано двойными тонкими линиями. Два координатных отрезка для точки Е составляют так называемую координатную ломаную, которая будет в дальнейшем широко применяться при построении точек, расположенных в пространстве. Большая ось эллипса E’G’ для круга, лежащего в плоскости х’О’у’, расположена горизонтально, а малая ось — вертикально.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451012_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В начертательной геометрии доказывается, что отношение осей эллипса, являющегося изображением окружности, в прямоугольной изометрии равняется 0,58, т. е. если большую ось эллипса d принять за единицу, то малая ось будет равна 0,58d. Это положение иллюстрируем так: расположим плоскость квадрата, в который вписана окружность, параллельно плоскости П₂ (рис. 157, а); повернем квадрат вокруг его горизонтальной диагонали на угол, равный 54° 30′ (рис. 157, б); спроецируем квадрат и окружность на плоскость, параллельную горизонтальной диагонали квадрата (рис. 157, е). Диагональ ромба и горизонтальный диаметр окружности спроецируются при этом в действительную величину, стороны ромба изобразятся прямыми, составляющими =0,82 от величины d; наклоненные диагональ и диаметр окружности спроецируются с искажением и составят 0,58 от своей действительной величины, поскольку sin 35°30′ = 0,58.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451023_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Изображение окружности на рис. 157, в является натуральным. Чтобы перейти к «приведенному» изображению, которое, как известно, увеличено в 1,22 раза, умножим все три величины на указанное количество раз. Получим: сторона ромба 0,82dxl,22 = 1,004d = d; большая ось эллипса dx 1,22 = 1,22d; малая ось эллипса 0,58dx1,22= 0,71d.

Зная эти зависимости, мы можем по заданному диаметру круга быстро найти размеры большой и малой осей эллипса, являющегося изометрической проекцией окружности. Пусть требуется построить прямоугольную изометрию круга, диаметр окружности которого равен 50 мм. Определяем размеры большой и малой осей эллипса: большая ось А’В’ равна 50х X 1,22 = 61 мм, малая ось CD’ равна 50’х0,71=35 мм. Строим по этим размерам оси эллипса на чертеже (рис. 158, а).

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451055_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Из геометрического черчения известно (см. рис. 47), что по осям эллипса можно построить его кривую. Практически эллипс в изометрии обычно заменяют овалом, который строят следующим образом (рис. 158, б). На большой А’В’ и малой CD’ осях строим две окружности; они пересекают продолжение малой оси в точках 1 и 2, а большую ось — в точках 3 и 4; эти точки являются центрами для дуг овала; используя их, вычерчиваем овал с радиусами r = О’В’—О’С и R = CD’ + г. Точку сопряжения дуг радиусов R и г находим, соединяя точки 1 и 4 прямой и продолжая эту прямую до пересечения с дугами в точке 5.

В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу и лишь расположены различно. В отличие от этого в прямоугольной диметрии имеются две различные формы эллипса: одна для плоскости х’О’z’, а другая — для плоскостей х’О’у’ и z’O’y’.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451008_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Пусть требуется построить прямоугольную диметрию окружности, лежащей в плоскости хОz (рис. 159, а). Описываем вокруг окружности квадрат и проводим его диагонали. Отмечаем точки пересечения диагоналей с окружностью и координатные отрезки, нужные для построения точек Е, F и др. Строим квадрат в прямоугольной диметрии (рис. 159, б), проводим его средние линии А’С и B’D’ и диагонали. Пользуясь координатными отрезками (помечены на чертежах тонкими двойными линиями), находим точки Е’, F’, G’ и H’. Большая ось эллипса F’G’ в прямоугольной диметрии будет равна l,06d, малая ось Е’Н’ будет равна 0,95d (отношение 9 : 10). Полученные восемь точек соединяем от руки, а затем обводим по лекалу. Если требуется более точное построение, то находят с помощью координатных ломаных еще ряд промежуточных точек.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451062_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В практике эллипс нередко заменяют овалом (рис. 160, а). Центры дуг для построения овала находим так: строим ромб, его средние линии и диагонали, Из центра О’ радиусом r=d/7 проводим вспомогательную окружность.

Она пересекает малую диагональ ромба в точках 1 и 2; используем эти центры для проведения дуг А’В’ и CD’. Соединяем точки А’ и I, С и 2; эти линии пересекают большую диагональ в точках 3 и 4. Пользуясь этими центрами, проводим дуги A’D’ и В’С. При этом способе также не требуется откладывать размеры большой и малой осей; они получаются сами собой при проведении дуг.

Если требуется построить прямоугольную диметрию окружности, лежащей в плоскости х’О’у’, то на осях х’ и у’ строим параллелограмм и намечаем средние точки его сторон (рис. 160, б). Затем через точку О’ проводим горизонтальную прямую — направление большой оси эллипса. Откладываем на этой прямой размер большой оси эллипса, равный 1,06d. Перпендикулярно к ней проводим малую ось эллипса, размер которой равен 0,35d (отношение 3 : 10). Таким путем получаем восемь точек, принадлежащих эллипсу. В практике избегают построения параллелограмма и строят вместо эллипса овал по его осям А’В’ и CD’ (рис. 160, в). Последовательность построения такая: от центра О’ на продолжении малой оси эллипса откладываем величину большой оси А’В’; получаем точку 1 — центр верхней дуги радиуса R. Тем же радиусом из точки 2 (не показана на чертеже) проводим нижнюю дугу овала. Слева и справа овал дочерчиваем кривыми радиуса r, величину которого принимаем равным r=O’C’/2 Центры 3 и 4 находим, делая засечки дугами r из точек А’ и В’. Точку сопряжения 5 находим, соединяя прямой точки I и 4 и продолжая эту прямую до пересечения с дугой.

Окружность, находящаяся в плоскости, параллельной фронтальной плоскости проекций, проецируется на нее во фронтальной изометрической проекции в виде окружности (рис. 161, а), а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в эллипсы, большие оси которых наклонены к осям х’ и z’ под углами 22° 30′. Большие оси эллипсов равны 1,3 диаметра окружности, малые — 0,54 диаметра окружности.

Пусть требуется построить во фронтальной изометрии окружность диаметра 40 мм, находящуюся в плоскости х’О’у’. Определяем большую и малую оси эллипса. Большая ось А’В’ = 1,3d = 1,3 40 = 52 мм, малая ось CD’ = 0,54d = 0,54-40 = 21,6 мм. Овал, заменяющий собой эллипс, удобно строить из четырех центров радиусами, равными R = 1,3d и r = = 0,16d (рис. 161, б). В нашем примере R — 52 мм, г = 0,16d = 6,4 мм. Точка 5 — точка сопряжения.

Источник

Как построить окружность?

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
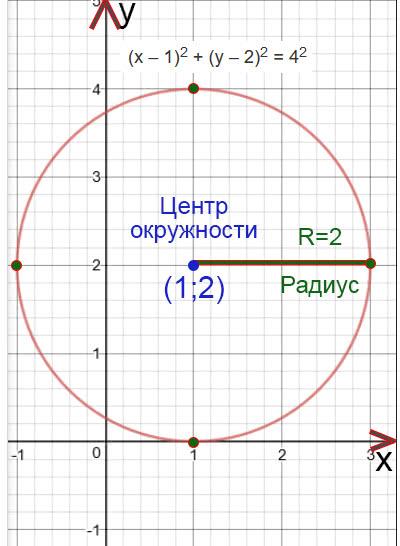
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Источник