Как построить недостающую проекцию точки
Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
Определение координат точек по их проекциям
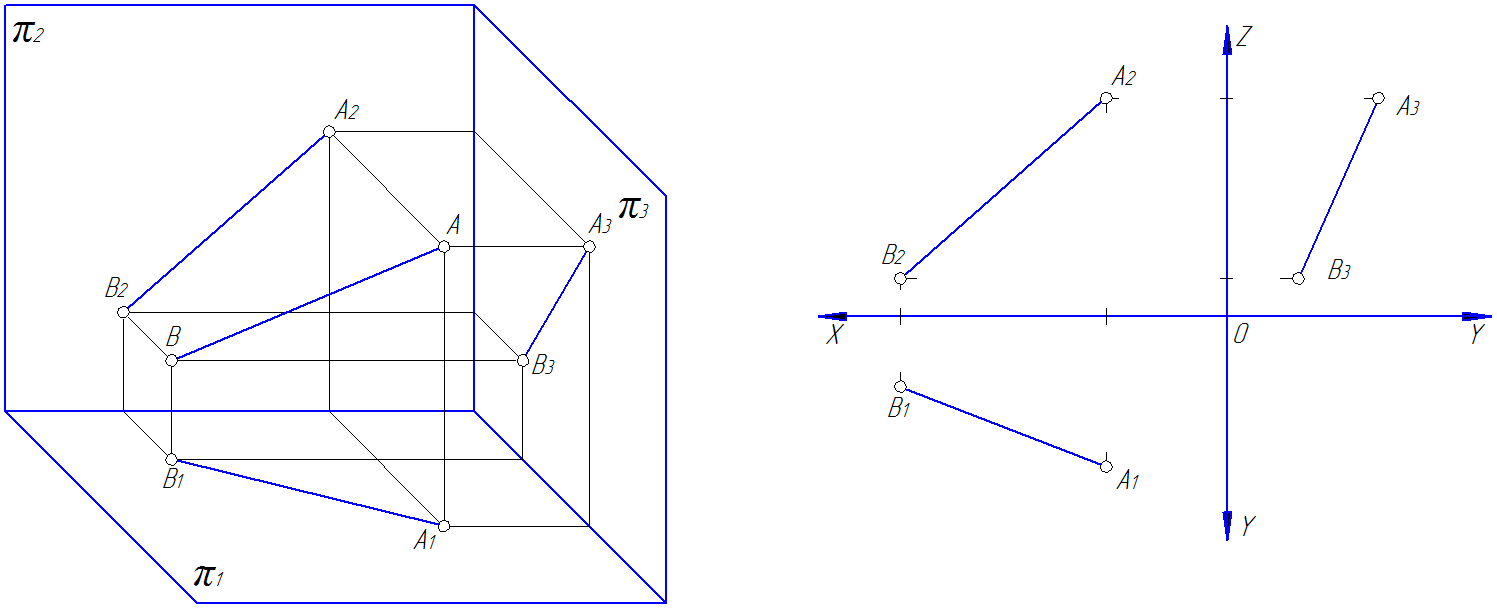
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A» имеет координаты х и z. Опустим перпендикуляр из A» на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Построение проекций точек
Точки A и B в плоскости П3 имеют следующие координаты: A»’ (y, z); B»’ (y, z). При этом A» и A»’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B» и B»’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A» к оси z. Точка пересечения этих двух перпендикуляров определяет положение A»’.
Точка B»’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B» к оси z. Точка пересечении этого перпендикуляра с осью z есть B»’.
Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Построение наглядного изображения точек в системе плоскостей П1, П2, П3
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Определение недостающих проекций точки.
На практике при решении позиционных задач возникают ситуации когда по двум известным проекциям необходимо определить на эпюре недостающею проекцию точки.
Для нахождения недостающей проекции точки, например точки А, используют вертикальную и горизонтальную линии связей и координату yА точки следующим образом (см. рис. 15).
1. Известны горизонтальная и фронтальная проекции точки А1 и А2, то для нахождения профильной проекции точки А3 через проекцию А2 проводят горизонтальную линию связи и от оси OZ откладывают координату yA.
2. Известны фронтальная и профильная проекции точки А2 и А3, то для нахождения горизонтальной проекции точки А1 через проекцию А2 проводят вертикальную линию связи и от оси OХ откладывают координату yA.
3. Известны горизонтальная и профильная проекции точки А1 и А3, то фронтальная проекция точки А2 лежит на пересечении вертикальной и горизонтальной линий связей, проходящих через А1 и А3 соответственно.
3.5. Контрольные вопросы
1. В чем заключается сущность метода двух изображений и чем он отличается от метода трех изображений?
2. Как осуществляется переход от аппарата проецирования к плоскому чертежу при методе двух изображений?
3. Характерные признаки точек частного положения на эпюре Монжа при методе двух изображений.
4. Характерные признаки точек общего и частного положений на эпюре при использовании метода двух изображений?
5. Какие точки называются конкурирующими и в чем заключается их конкуренция?
6. Характерный признак конкурирующих точек на эпюре и порядок определения видимости их проекций.
7. В чем заключается сущность прямой и обратной задач для точки.
8. Как определяется недостающая горизонтальная проекция точки?
9. Как определяется недостающая фронтальная проекция точки?
10. Как определяется недостающая профильная проекция точки?
Лекция 4. ПРЯМАЯ НА ЭПЮРЕ МОНЖА
4.1. Задание прямой на эпюре.
4.2. Характеристика прямых.
4.3. Определение точки принадлежащей прямой.
4.4. Деление отрезка прямой в заданном соотношении.
4.4. Контрольные вопросы.
Задание прямой на эпюре
Чтобы построить прямую на эпюре необходимо на прямой взять две точки и спроецировать их на плоскости проекций (рис. 28). Затем проведя прямые через одноименные проекции точек получим проекции прямой.
 Рис. 29 Рис. 29 |
В общем случае прямые в пространстве могут задаваться (рис. 29) двумя точками (точки А и В), отрезком ([АВ]) или точкой и направлением прямой (например, точкой А и условиями, характеризующими направление прямой).
Примечание. В последующем все эпюры будут выполнятся методом двух изображений и только при необходимости будет использоваться полное проецирование (метод трех изображений).
Характеристика прямых
Все прямые пространства подразделяются на прямые общего и частного положений.
Прямая общего положения. Прямая общего положения не параллельны и не перпендикулярны ни одной из плоскостей проекций.
Примеры таких прямых показаны на рис. 28 и 29.
Особенностью изображения этих прямых является то, что на эпюре проекции прямой составляют с осями проекций произвольные углы и поэтому величина каждой проекции меньше истинной величины самой прямой (рис. 28).
Прямая частного положения. Прямые, параллельные или перпендикулярные плоскостям проекций называют прямыми частного положения.
Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня.
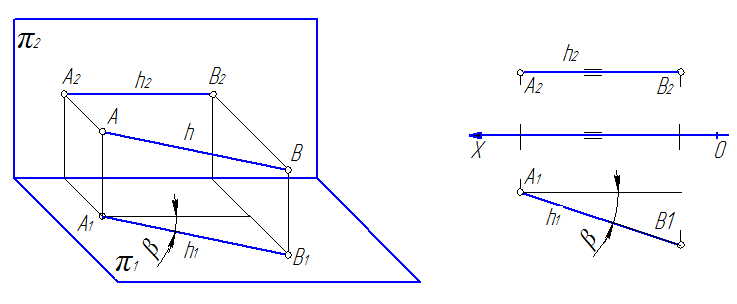
1. Прямые, параллельные горизонтальной плоскости проекций; называют горизонтальными или горизонталями h (рис. 30).
Характерным признаком таких прямых на эпюре является то, что их фронтальные проекции параллельны оси 0Х.
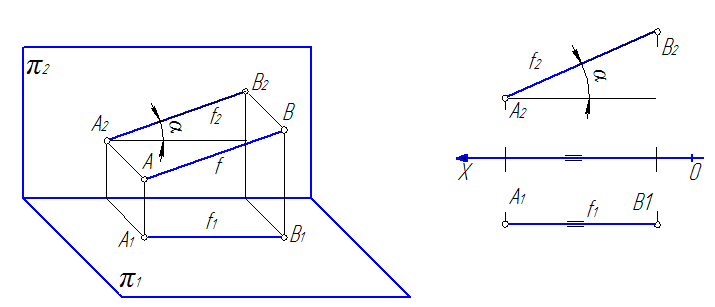
2. Прямые, параллельные фронтальной плоскости проекций; называют фронтальными или фронталями f (рис. 31).
Характерным признаком таких прямых на эпюре является то, что их горизонтальные проекции параллельны оси 0Х.
3. Прямую, параллельную профильной плоскости проекций, называют профильной р (рис. 32).
Характерным признаком таких прямых на эпюре является то, что их горизонтальные и фронтальные проекции перпендикулярны оси 0Х.
Следует отметить, что каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона a и b, которые эта прямая образует с двумя другими плоскостями проекций, так же будут проецироваться на эту плоскость без искажения.
Так на рис. 30 проекция [A1B1]=[AB], а угол b – угол наклона отрезка [AB] к плоскости π2. На рис. 31 проекция [A2B2]=[AB], а угол a – угол наклона отрезка [AB] к плоскости π1. На рис. 32 видно, что все проекция [A2B2]=[AB], а углы a и b – углы наклона отрезка [AB] к плоскостям π1 и π1 соответственно.
Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевыми горизонталями, нулевыми фронталями и нулевыми профильными прямыми.
Прямые, перпендикулярные к одной из плоскостей проекций называются проецирующими:
1) горизонтально-проецирующая – прямая l, перпендикулярная к горизонтальной плоскости проекций (рис. 33);
2) фронтально-проецирующая – прямая m, перпендикулярная к фронтальной плоскости проекций (рис. 34);
3) профильно-проецирующая – прямая n, перпендикулярная к профильной плоскости проекций (рис. 35).
На рис. 33 34 и 35 видно, что проекции прямых, перпендикулярных к плоскостям проекций, на этих плоскостях представляют собой точки, а на тех плоскостях, которым прямые параллельны, проекции прямых будут перпендикулярны к осям и равны по величине самим прямым.
Как построить недостающую проекцию точки
Проекции плоскости на комплексном чертеже будут различны в зависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана: а) тремя точками, не лежащими на одной прямой; б) прямой линией и точкой, лежащей вне этой прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми.
На рис. 100 плоскость задана прямыми линиями, по которым эта плоскость пересекает плоскости проекций. Такие линии называются следами плоскости.
Линия пересечения данной плоскости Р с горизонтальной плоскостью проекций Н называется горизонтальным следом плоскости Р и обозначается Рн.
Линия пересечения плоскости Р с фронтальной плоскостью проекций V называется фронтальным следом этой плоскости и обозначается Рv.
Линия пересечения плоскости Р с профильной плоскостью проекций W называется профильным следом этой плоскости и обозначается Pw.
Следы плоскости пересекаются на осях проекций. Точки пересечения следов плоскости с осями проекций называются точками схода следов. Эти точки обозначаются Рx, Рy и Рz.
Горизонтальная, фронтальная и профильная плоскости, перпендикулярные к двум плоскостям проекций, называются плоскостями уровня. Если на комплексном чертеже плоскость уровня задана не следами, а какой-нибудь плоской фигурой, например, треугольником или параллелограммом (рис. 101, г, д, е), то на одну из плоскостей проекций эта фигура проецируется без искажения, а на две другие плоскости проекций — в виде отрезков прямых.
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
Плоскость, перпендикулярная к плоскости Н (рис. 102, а),называется горизонтально-проецирующей плоскостью. Фронтальный след Pv этой плоскости перпендикулярен оси Ох, а горизонтальный след Рн расположен под углом к оси Ох (комплексный чертеж на рис. 102, а)
Если горизонтально-проецирующая плоскость задана не следами, а какой-либо фигурой, например треугольником АВС (рис. 102, 6), то горизонтальная проекция этой плоскости представляет собой прямую линию, а фронтальная и профильная проекции — искаженный вид треугольника АВС.
Фронтально-проецирующей плоскостью называется плоскость, перпендикулярная к фронтальной плоскости проекций (рис. 102, в).
Горизонтальный след этой плоскости перпендикулярен оси Ох, а фронтальный след расположен под некоторым углом к оси Ох (комплексный чертеж на рис. 102, в).
При задании фронтально-проецирующей плоскости не следами, а, например, параллелограммом ABCD фронтальная проекция такой плоскости представляет собой прямую линию (рис. 102, г), а на горизонтальную и профильную плоскости проекций параллелограмм проецируется с искажением.
Профильно-проецирующей плоскостью называется плоскость, перпендикулярная к плоскости W (рис. 102, д). Следы Pv и Рн этой плоскости параллельны оси Ох.
При задании профильно-проецирующей плоскости не следами, а, например, треугольником АВС (рис. 102, е) профильная проекция такой плоскости представляет собой прямую линию. Плоскости, перпендикулярные двум плоскостям проекций, как было сказано, называются плоскостями уровня.
Если плоскость Р не перпендикулярна ни одной из плоскостей проекций (рис. 102, ж), то такая плоскость называется плоскостью общего положения. Все три
следа Pv, Рн и Pw плоскости Р наклонены к осям проекций.
Если плоскость общего положения задана не следами, а, например, треугольником АВС (рис. 102, з), то этот треугольник проецируется на плоскости H, V и W в искаженном виде.
ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ
Если прямая расположена на плоскости, то она должна проходить через две какие-либо точки, принадлежащие этой плоскости. Такие две точки могут быть взяты на следах плоскости — одна на горизонтальном, а другая на фронтальном. Так как следы прямой и плоскости находятся на плоскостях проекций и то следы прямой, принадлежащей плоскости, должны быть расположены на одноименных следах этой плоскости (рис. 103, а);например, горизонтальный след Н прямой — на горизонтальном следе плоскости, фронтальный след V прямой — на фронтальном следе Рv плоскости (рис. 103, б).
Для того чтобы на комплексном чертеже плоскости Р, заданной следами, провести какую-либо прямую общего положения, необходимо наметить на следах плоскости точки v’ или считать их следами искомой прямой (точнее, v’ — фронтальной проекцией горизонтального следа прямой).
Опустив перпендикуляры из v’ и на ось проекций х, находим на ней вторые проекции следов прямой: v — горизонтальную проекцию фронтального следа прямой и h’ — фронтальную проекцию горизонтального следа прямой. Соединив одноименные проекции следов, т. е. v’c h и v c h прямыми, получим две проекции прямой линии, расположенной в плоскости общего положения Р.
Очень часто требуется провести на плоскости горизонталь и фронталь, которые называются главными линиями плоскости или линиями уровня. Главные линии помогают решать многие задачи проекционного черчения.
Горизонталь и фронталь имеют в системе двух плоскостей V и Н только по одному следу (например, горизонталь имеет только фронтальный след). Поэтому, зная один след главной линии, проекцию главной линии проводят по заранее известному направлению. Это направление для горизонтали видно из рис. 104, а, где показана плоскость общего положения и горизонталь, лежащая на ней. Из рисунка видно, что горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.
Таким образом, чтобы на комплексном чертеже плоскости Р провести в этой плоскости какую-либо горизонталь, нужно наметить на следе Рv плоскости точку v’ (рис. 104, б) и считать ее фронтальной проекцией фронтального следа горизонтали. Затем через точку v’ параллельно оси х проводят прямую, которая будет фронтальной проекцией горизонтали.
11 с редко требуется провести горизонталь и фронталь на проецирующих плоскостях. Рассмотрим, например, построение горизонтали на фронтально-проецирующей плоскости (рис. 105). На следе плоскости Рv намечаем фронтальную проекцию фронтального следа горизонтали и на оси находим его горизонтальную проекцию v (рис. 105, а). Затем через точку проводим параллельно Рн горизонтальную проекцию горизонтали; фронтальная проекция горизонтали совпадает с точкой v’.
Если плоскость задана не следами, а пересекающимися или параллельными прямыми, то построение проекций горизонтали или фронтали, расположенных в этой плоскости, выполняется следующим образом.
Пусть плоскость задана двумя параллельными прямыми AВ и СD (рис. 105, 6). Для построения горизонтали, лежащей в этой плоскости, проводим параллельно оси х фронтальную проекцию горизонтали и отмечаем точки е’и f’ пересечения фронтальной проекции горизонтали с фронтальными проекциями параллельных прямых, которыми задана плоскость. Через точки е’и f’ проводим вертикальные линии связи до пересечения с ab и cd в точках е и f. Точки е и f соединяем прямой линией, которая и будет горизонтальной проекцией горизонтали.
Если требуется найти следы плоскости, заданной пересекающимися или параллельными прямыми, надо найти следы этих прямых и через полученные точки провести искомые следы плоскости.
Рассмотрим комплексный чертеж параллелограмма ABCD (рис. 106, a),который задает некоторую плоскость X. Отрезок DC расположен в плоскости H, следовательно, его горизонтальная проекция dc является горизонтальным следом плоскости (точнее — горизонтальной проекцией горизонтального следа плоскости).
Чтобы найти фронтальный след этой плоскости, необходимо продолжить горизонтальную проекцию dc прямой DC до пересечения с осью х в точке Рх, через которую должен пройти искомый фронтальный след плоскости.
Второй точкой v’, через которую пройдет искомый фронтальный след плоскости, является фронтальный след прямой АВ (фронтальная проекция фронтального следа). Фронтальную проекцию фронтального следа прямой АВ находим, продолжая горизонтальную проекцию ab прямой АВ до пересечения с осью х в точке v, которая будет горизонтальной проекцией искомого фронтального следа прямой АВ. Фронтальная проекция фронтального следа этой прямой находится на перпендикуляре, восставленном из точки v к оси х, в точке v’ его пересечения с продолжением фронтальной проекции а’в’ прямой АB. Соединив точки Px с v’, находим фронтальный след Pv плоскости.
Пример решения подобной задачи приведен на рис 106, б.
Часто на комплексных чертежах приходится решать такую задачу: по одной из заданных проекций точки, расположенной на заданной плоскости, определить две другие проекции точки. Ход решения задачи следующий.
Через заданную проекцию точки, например фронтальную проекцию n’ точки N, расположенной на плоскости треугольника АВС (рис. 107), проводим одноименную проекцию вспомогательной прямой любого направления, например m’к’.
Горизонталью плоскости называется прямая, принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций Н.
Строим другую проекцию mк вспомогательной прямой. Для этого проводим вертикальные линии связи через точки m’ и к’ до пересечения с линиями ас и вс. Из точки n’ проводим линию связи до пересечения с проекцией mк в искомой точке n.
Профильную проекцию n» находим по общим правилам проецирования.
В качестве вспомогательной прямой для упрощения построения чаще используются горизонталь или фронталь.
Проводим проекции горизонтали: фронтальную — через v’ параллельно оси х, горизонтальную — через v параллельно следу Рн плоскости Р. На фронтальной проекции горизонтали намечаем фронтальную проекцию а’ искомой точки и, проводя вертикальную линию связи, определяем горизонтальную проекцию а точки А.
Если точка лежит на проецирующей плоскости, то построение ее проекций упрощается. В этом случае одна из проекций точки всегда расположена на следу плоскости (точнее, на его проекции). Например, горизонтальная проекция а точки А, расположенной на горизонтально-проецирующей плоскости Р, находится на горизонтальной проекции горизонтального следа плоскости (рис. 108, в и г)
Если точка расположена на фронтально-проецирующей плоскости Р (рис. 108, д и е), то ее фронтальная проекция а’ находится на фронтальном следе Хv плоскости Р.
ПРОЕКЦИИ ПЛОСКИХ ФИГУР
Зная построение проекций прямых и точек, расположенных на плоскости, можно построить проекции любой плоской фигуры, например, прямоугольника, треугольника, круга.
Как известно, каждая плоская фигура ограничена отрезками прямых или кривых линий, которые могут быть построены по точкам.
Проекции фигуры, ограниченной прямыми линиями (треугольника и многоугольника), строят по точкам (вершинам). Затем одноименные проекции вершин соединяют прямыми линиями и получают проекции фигур.
Проекции круга или другой криволинейной фигуры строят при помощи нескольких точек, которые берут равномерно по контуру фигуры. Одноименные проекции точек соединяют плавной кривой по лекалу.
Проекции плоской фигуры строят различными способами в зависимости от положения фигуры относительно плоскостей проекций и Наиболее просто построить проекции фигуры, расположенной параллельно плоскостям Н и V; сложнее — при расположении фигуры на проецирующей плоскости или на плоскости общего положения.
Рассмотрим несколько примеров.
Если треугольник АВС расположен на плоскости, параллельной плоскости H (рис. 109, a), то горизонтальная проекция этого треугольника будет его действительным видом, а фронтальная проекция — отрезком прямой, параллельным оси х. Комплексный чертеж треугольника АВС показан на рис. 109, 6. Такой треугольник можно видеть на изображении резьбового резца (рис. 109, в),передняя грань которого треугольная.
Трапеция ABCD расположена на фронтально-проецирующей плоскости (рис. 110, а). Фронтальная проекция трапеции представляет собой отрезок прямой линии, а горизонтальная — трапецию (рис. 110, б)
Задняя грань отрезного резца (рис. 110, в) имеет форму трапеции.
Рассматривая плоскость, параллельную горизонтальной, фронтальной или профильной плоскости проекций (плоскость уровня), можно заметить, что любая фигура, лежащая в этой плоскости, имеет одну из проекций, представляющую собой действительный вид этой фигуры; вторая и третья проекции фигуры совпадают со следами этой плоскости.
Рассматривая проецирующую плоскость, заметим, что любая точка, отрезок прямой или кривой линии, а также фигуры, расположенные на проецирующей плоскости, имеют одну проекцию, расположенную на следе этой плоскости. Например, если круг лежит на фронтально-проецирующей плоскости Р (рис. 111), то фронтальная проекция круга совпадает с фронтальным следом Pv плоскости Р. Две другие проекции круга искажены и представляют собой эллипсы. Большие оси эллипсов равны проекциям диаметра круга 37. Малые оси эллипсов равны проекциям диаметра круга 15, перпендикулярного диаметру 37.
На рис. 111,6 показано колено трубы с двумя фланцами. Горизонтальная проекция контура нижнего фланца, который расположен в горизонтальной плоскости, будет действительным видом окружности. Горизонтальная проекция контура верхнего фланца изобразится в виде эллипса.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Две плоскости могут быть взаимно параллельными или пересекающимися.
Из стереометрии известно, что если две параллельные плоскости пересекают какую-либо третью плоскость, то линии пересечения этих плоскостей параллельны между собой. Исходя из этого положения, можно сделать вывод, что одноименные следы двух параллельных плоскостей Р и Q также параллельны между собой.
Если даны две профильно-проецирующие плоскости Р и К (рис. 112, а), то параллельность их фронтальных и горизонтальных следов на комплексном чертеже в системе V и Н недостаточна для того, чтобы определить, параллельны эти плоскости или нет. Для этого необходимо построить их профильные следы в системе V, Н и W (рис. 112, б). Плоскости Р и K будут параллельны только в том случае, если параллельны их профильные следы Pw и Kw.
Одноименные следы пересекающихся плоскостей Р и Q (рис. 112, в) пересекаются в точках V и H, которые принадлежат обеим плоскостям, т. е. линии их пересечения. Так как эти точки расположены на плоскостях проекций, то, следовательно, они являются также следами линии пересечения плоскостей. Чтобы на комплексном чертеже построить проекции линии пересечения двух плоскостей Р и Q, заданных следами Pv, Рн и Qv,Qh, необходимо отметить точки пересечения одноименных следов плоскостей, т. е. точки v’ и h (рис. 112, г); точка v’ — фронтальная проекция фронтального следа искомой линии пересечения плоскостей Р и Q, h — горизонтальная проекция горизонтального следа этой же прямой. Опуская перпендикуляры из точек v’ и h на ось х, находим точки v и h’. Соединив прямыми одноименные проекции следов, т. е. точки v’ и h’, v и h’ получим проекции линии пересечения плоскостей Р и Q.
ПРЯМАЯ, ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ
Для этого фронтальную проекцию отрезка m’n’ продолжаем до пересечения с отрезками a’b’ и c’d’ (проекциями сторон треугольника АВС), получаем точки (рис. 113, б).
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ
Если прямая АВ пересекается с плоскостью Р, то на комплексном чертеже точка их пересечения определяется следующим образом.
Вспомогательная плоскость Q пересекает данную плоскость Р по прямой VH, следы которой лежат на пересечении следов плоскостей Р и Q. Заметив точки пересечения следов Pv и Qv — точку v’ и следов Qн и PH — точку h,опускают из этих точек на ось х перпендикуляры, основания которых — точки v’ и h’ — будут вторыми проекциями следов прямой VH. Соединяя точки v’и h’, v и h, получают фронтальную и горизонтальную проекции линии пересечения плоскостей.
Точка пересечения М заданной прямой AB и найденной прямой VH и будет искомой точкой пересечения прямой АВ с плоскостью Р. Фронтальная проекция m’ этой точки расположена на пересечении проекций a’b’ и v’h’. Горизонтальную проекцию m точки М находят, проводя вертикальную линию связи из точки m’ до пересечения с ab.
Если плоскость задана не следами, а плоской фигурой, например, треугольником (рис. 114, 6), то точку пересечения прямой MN с плоскостью треугольника АВС находят следующим образом.
Затем находят линию ED пересечения плоскости Р с плоскостью данного треугольника ABC. Фронтальная проекция e’d’ линии ED совпадает с m’n’. Горизонтальную проекцию ed находят, проводя вертикальные линии связи из точек е’и d’ до встречи с проекциями ab и ас сторон треугольника АВС. Точки e и d соединяют прямой. На пересечении горизонтальной проекции ed линии ED с горизонтальной проекцией прямой MN находят горизонтальную проекцию k искомой точки К. Проведя из точки k вертикальную линяю связи, на ходят фронтальную проекцию k’ Точка К — искомая точка пересечения прямой МК с плоскостью треугольника АВС.
В частном случае прямая может быть перпендикулярна плоскости Р.Из условия перпендикулярности прямой к плоскости следует, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим на этой плоскости (в частности, этими прямыми могут быть следы плоскости). Тогда проекции прямой АВ будут перпендикулярны одноименным следам этой плоскости (рис 115, а) Фронтальная проекция а’b’ перпендикулярна фронтальному следу Ру, а горизонтальная проекция ab перпендикулярна горизонтальному следу Рн плоскости Р.
Если плоскость задана параллельными или пересекающимися прямыми, то проекции прямой, перпендикулярной этой плоскости, будут перпендикулярны горизонтальной проекции горизонтали и фронтальной проекции фронтали, лежащих на плоскости.
Таким образом, если, например, на плоскость, заданную треугольником АВС необходимо опустить перпендикуляр, то построение выполняется следующим образом (рис. 115, б).
На плоскости проводят горизонталь СЕ и фронталь FA. Затем из заданных проекций d и d’ точки D опускают перпендикуляры соответственно на ce и f’a’. Прямая, проведенная из точки D будет перпендикулярна плоскости треугольника АВС.
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Задачи на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение плоскости с прямыми линиями. На рис. 116 показано построение линии пересечения плоскостей, заданных треугольниками АВС и DEF. Прямая MN построена по найденным точкам пересечения сторон DE и EF треугольника DEF с плоскостью треугольника АВС.
Например, чтобы найти точку M, через прямую DF проводят фронтально-проецирующую плоскость Р, которая пересекается с плоскостью треугольника АВС по прямой 12. Через полученные точки 1′ и 2′ проводят вертикальные линии связи до пересечения их с горизонтальными проекциями ав и ас сторон треугольника АВС в точках 1 и 2. На пересечении горизонтальных проекций df и 12 получают горизонтальную проекцию m искомой точки М, которая будет точкой пересечения прямой DF с плоскостью АВС. Затем находят фронтальную проекцию m’ точки M. Точку N пересечения прямой EF с плоскостью АВС находят так же, как и точку М.
Соединив попарно точки m’ и n’, m и n, получают проекции линий пересечения MN плоскостей АВС и DEF.