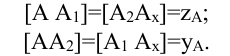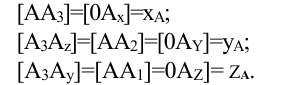Как построить недостающие проекции точек
Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
Определение координат точек по их проекциям
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A» имеет координаты х и z. Опустим перпендикуляр из A» на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Построение проекций точек
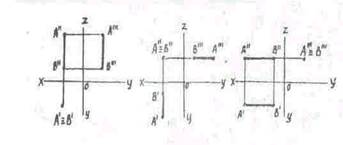
Точки A и B в плоскости П3 имеют следующие координаты: A»’ (y, z); B»’ (y, z). При этом A» и A»’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B» и B»’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A» к оси z. Точка пересечения этих двух перпендикуляров определяет положение A»’.
Точка B»’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B» к оси z. Точка пересечении этого перпендикуляра с осью z есть B»’.
Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
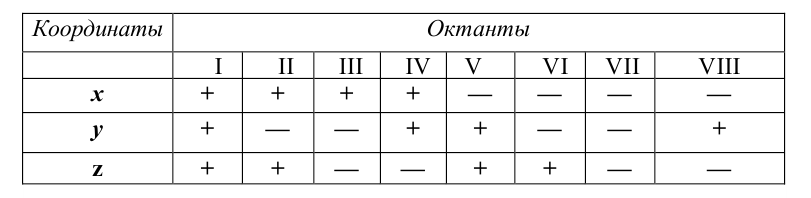
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Построение наглядного изображения точек в системе плоскостей П1, П2, П3
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Прямая и точка в плоскости. Построение недостающих проекций.
Кчислу основных задач, решаемых на плоскости, относят:
· проведение любой прямой в плоскости;
· построение в плоскости некоторой точки;
· построение недостающей проекции точки;
· проверка принадлежности точки плоскости.
Решение этих задач основывается на известных положениях геометрии:
прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости, или через одну точку этой плоскости параллельно прямой, лежащей в этой плоскости или ей параллельной. При этом используется известное условие, что если точка принадлежит плоскости, то ее проекции лежат на одноименных проекциях прямой, принадлежащей плоскости.
Проведение любой прямой в плоскости.Для этого достаточно (рис. 3.10) на проекциях плоскости взять проекции двух произвольных точек, например a’, а и 1′, 1,и через них провести проекции a’1′, а–1 прямой А–1.На рисунке 3.11 проекции b’1′, b–1 прямой В–1 проведены параллельно проекциям a’c’, ас стороны AС треугольника, заданного проекциями a’b’c’, abc. Прямая В–1 принадлежит плоскости треугольника ABC.
Построение в плоскости некоторой точки.Для построения в плоскости точки в ней проводят вспомогательную прямую и на ней отмечают точку.На чертеже (рис. 3.12) плоскости, заданной проекциями a’, а точки, b’c’, bc прямой, проведены проекции а’1′, а–1 вспомогательной прямой, принадлежащей плоскости. На ней отмечены проекции d’, d точки D,принадлежащей плоскости.
Рис.3.10 Рис.3.11 Рис.3.12
Построение недостающей проекции точки.На рисунке 3.13 плоскость задана проекциями a’b’c’, abc треугольника. Принадлежащая этой плоскости точка D задана проекцией d’.Следует достроить горизонтальную проекцию точки D.Ее строят с помощью вспомогательной прямой, принадлежащей плоскости и проходящей через точку D.Для этого проводят, например, фронтальную проекцию b’1’d’ прямой, строят ее горизонтальную проекцию b–1 и на ней отмечают горизонтальную проекцию d точки.
Проверка принадлежности точки плоскости.Для проверки принадлежности точки плоскости используют вспомогательную прямую, принадлежащую плоскости. Так, на рисунке 3.14 плоскость P задана проекциями a’b’, ab и c’d’, cd параллельных прямых, точка – проекциями e’, е.Проекции вспомогательной прямой проводят так, чтобы она проходила через одну из проекций точки. Например, фронтальная проекция 1’2′ вспомогательной прямой проходит через проекцию e’.Построив горизонтальную проекцию 1–2 вспомогательной прямой, убеждаемся, что точка E не принадлежит плоскости Р.
13.Прямые особого положения в плоскости. Главные линии плоскости.
К прямым, занимающим особое положение в плоскости, относят горизонтали, фронтали, профильные прямые и линии наибольшего наклона к плоскостям проекций. Эти линии называют главными линиями плоскости.
Горизонталь – прямая, лежащая в плоскости и параллельная плоскости проекций H.На рисунке 3.15 проекции горизонтали проведены через проекции c’, с точки С и 1‘, 1 точки 1 прямой AB плоскости, заданной проекциями точки С и прямой AB.Фронтальная проекция c’1′ горизонтали параллельна оси x.
Рис.3.15 Рис.3.16
Фронталъ – прямая, лежащая в плоскости и параллельная плоскости проекций V.На рисунке 3.16 проекции фронтали проведены через проекции 1′, 1 и 2′, 2 точек 1 и 2 проекций а’b’, ab, c’d’, cd параллельных прямых AB и CB заданной плоскости. Горизонтальная проекция 1 – 2 фронтали параллельна оси x.
Линиями наибольшего наклона плоскости к плоскостям H, V и W называют прямые, лежащие в ней и перпендикулярные или к горизонталям плоскости, или к ее фронталям, или к ее профильным прямым.Соответственно определяется наклон плоскости к плоскостям H, V или W.
Рассмотрим линию наибольшего наклона к плоскости H, называемую линией ската.
Линия ската BK плоскости Q и горизонталь С–1 показаны на рисунке 3.17: BK 

Вначале на горизонтальной проекции а проведен перпендикуляр а–2 к проекции с–1 горизонтали, построена фронтальная проекция 2′ точки 2 и через нее проведена фронтальная проекция a’2′ линии ската.
Угол между линией ската и ее горизонтальной проекцией является линейным углом между плоскостью, которой принадлежит линия ската, и плоскостью проекций H.
Построения недостающих проекций точек
Точка в пространстве определяется своими координатами, которые, как правило, имеют числовые значения, например А (х, у, z), А (10, 45, 15). Прямоугольные проекции точки на плоскостях проекций определяются
как основания перпендикуляров, опущенных с точки на каждую с плоскостей проекций. Проекции точек обозначаются большими буквами латинского алфавита или числами. А’ — горизонтальная проекция точки А;
 |
А» — фронтальная проекция точки А;
А'» — профильная поекция точки А. Для получения проекционного чертежа совмещают плоскости П и П с
(фронтальной плоскостью проекций П поворотом соответственно около осей Х и
Z. Тогда на чертеже проекции А’ и А» размещаются на одном перпендикуляре к оси ОХ, а А» и А'» — на одном перпендикуляре к оси OZ. Известно три способа
построения профильной проекции точки по данным двум проекциям.
Прямая линия общего и частного положения на эпюре
 |
Монжа.
Для того, чтобы выполнить чертеж прямой, необходимо
найти проекции двух её точек. В начертательной геометрии,
в зависимости от положения прямых относительно
плоскостей проекций, они могут иметь свое название —
прямые общего и частного положения. Прямая не параллельная ни одной с плоскостей проекций, назы-
вается прямой общего положения. Прямые частного положения бывают параллельными или перпендикулярными плоскостям проекций. Прямые, параллельные одной из плоскости проекций, делятся на: горизонтальные прямые — параллельные горизонтальной плоскости проекций; фронтальные прямые— параллельные фронтальной плоскости проекций; профильные прямые — параллельные профильной плоскости проекций. Прямые, перпендикулярные одной из плоскостей проекций, делятся на: горизонтально-проецирующие прямые, перпендикулярные горизонтальной плоскости проекций; фронтально-проецирующие прямые, перпендикулярные фронтальной плоскости проекций; профильно-проецирующие прямые, перпендикулярные профильной плоскости проекций.
 |
4. Следы прямой линии. Сформулировать последовательность построения горизонтальною и фронтального следов прямой.
Следом прямой линии называется точка пересечения прямой с соответствующей плоско-. стью проекций. Для определения горизонтального следа М (М’, М») прямой АВ (А’В’, А»В») надо:
продлить фронтальную проекцию А»В» до
пересечения с-осью ОХ (М»), затем повести перпендикуляр к оси ОХ до пересечения с продолжением горизонтальной проекции А’В’. Для определения фронтального следа N (N’, N») прямой надо: продлить горизонтальную проекцию А’В’ до пересечения с осью ОХ, затем провести перпендикуляр к оси ОХ до пересечения с подолжением фронтальной проекции А»В». М (М’, М») — горизонтальный след рпямой АВ (А’В’, А»В»);
N (N’, N») — фронтальный след прямой АВ (А’В’, А»В»).
Построение недостающих проекций точек на поверхностях детали
Нахождение недостающих проекций точек на поверхностях детали производят в следующей последовательности.
1. Определяют вид поверхности, которой принадлежит точка.
2. Уясняют какие простые линии (окружность или прямую) можно провести на данной поверхности через заданную точку.
3. Вспоминают условие принадлежности точки поверхности: точкапринадлежит поверхности, если она принадлежит любой линии на ней.
4. Выбирают простую линию (окружность или прямую) на поверхности, проходящую через точку.
5. Проводят проекцию этой линии через известную проекцию искомой точки.
6. Строят вторую проекцию этой линии.
7. На построенной проекции линии с помощью линии связи находят недостающую проекцию точки, учитывая при этом видимость известной проекции точки. Рассмотрим изложенное выше на примере.
Пример. На рис. 2.116,а изображены главный вид и вид сверху детали. На главном виде заданы фронтальные проекции видимых 19,39,59,7C и невидимых (29), (49), (69),(8C),(9C) точек, находящихся на поверхности детали. Построить горизонтальные проекции этих точек на виде сверху.
Деталь состоит из торовой Т, сферической С, цилиндрическойЦ, конической К и пирамидальной ПР поверхностей. Простыми линиями на первых четырёх поверхностях являются окружности параллельные горизонтальной плоскости проекций. Они проецируются на главном виде в отрезки, перпендикулярные к оси детали, а на виде сверху в окружности. Простыми линиями на пирамидальной поверхности являются прямые линии. С помощью указанных линий, проходящих через искомые точки, и будем находить недостающие их проекции.
Точки 1 и (2) принадлежат торовой поверхности. Проведём через их проекции 19 и (29) фронтальную проекцию окружности К9, которая проецируется в отрезок. Строим еёгоризонтальную проекцию, которая представляет собой окружность К, и на ней с помощью линии связи, проходящей через проекции точек 19=(29), построим горизонтальные проекции 1 и 2 этих точек с учётом их видимости на главном виде.
Аналогично строят недостающие проекции точек 39=(49) с помощью проекций окружности l9 и l, проходящей через эти точки, а также точек 79 и (89) с помощью проеций окружности m9 и m.
Точки 5 и 6 находят с помощью линии связи на горизонтальной проекции окружности, в которую проецируется поверхность цилиндра.
Точка (99) находится на грани пирамиды. Проводим в этой грани фронтальную проекцию прямой n9 через вершину основания пирамиды и точку (99). Находим с помощью линий связи горизонтальную проекцию этой прямой и на ней с помощью линии связи горизонтальную проекцию точки 9.
Следует иметь в виду, что если на поверхностях ( кроме цилиндрической) заданы горизонтальные проекции упомянутых выше точек, то их фронтальные проекции находят с помощью этих же линий на поверхностях, начиная с горизонтальной плоскости проекций, а указанное стрелками направление решения меняется на противоположное.
2.7 Построение третьего вида по двум заданным
При выполнении чертежей предметов часто приходится строить третье изображение по двум заданным. Это требует умения читать чертеж, определять поверхности, ограничивающие предмет, и линии их пересечения. Рассмотрим два примера таких построений.
Пример 1. Построение третьего вида предмета по двум заданным. На рис. 2.117 заданными являются главный вид и вид сверху. Необходимо построить вид слева.
Предмет содержит: первый верхний цилиндр вращения, половина которого срезана профильной плоскостью; второй цилиндр вращения меньшего диаметра, в котором выполнен вырез фронтальной и профильной плоскостями на части его высоты; призму сложной конфигурации сдвумя выступами и двумя ребрами жесткости в виде усеченных четырехугольных призм.
Для построения третьего вида (вида слева) на заданных двух видах обозначены проекции характерных точек 1…24. Имея две проекции каждой точки строится третья их проекция на виде слева. Построенные точки соединены линиями, которые они определяют.
Пример 2. Построение недостающей третьей проекции предмета по двум заданным с выполнением разрезов. На рис. 2.118 заданы главный вид и вид сверху. Необходимо достроить вид слева для выявления полной формы предмета без штриховых линий с использованием необходимых для этого разрезов и сечений.
Прежде чем приступить к построению, необходимо прочитать чертеж, т.е. мысленно расчленить этот предмет на составляющие его элементы и определить их поверхности. Чтобы правильно прочитать чертеж, необходимо знать, как образуются поверхности всех элементов, составляющих предмет, и как изобразить их на чертеже, а также уметь определять линии их взаимного пересечения.
Рассматривая заданное изображение, устанавливаем, что контуры изображений ряда элементов предмета ограничены прямыми линиями. Это значит, что эти элементы предмета ограничены такими поверхностями, которые могут проецироваться на две плоскости проекций в две прямые линии или в прямую и плоскую фигуру (прямоугольник). Такими поверхностями могут быть только плоскости. В первом случае плоскости будут перпендикулярны к этим плоскостям проекций, а во втором — параллельны одной из них.
Устанавливаем также, что пять элементов предмета на горизонтальную плоскость проекций проецируются в виде окружности, а на фронтальную — в виде прямоугольника. Так изображается на двух взаимно перпендикулярных плоскостях прямой круговой цилиндр с осью, перпендикулярной к горизонтальной плоскости проекций.
Один элемент на главном виде проецируется в виде окружности, а на виде сверху как прямоугольник. Это круговой цилиндр, ось которого перпендикулярна к фронтальной плоскости проекций.
Также видим, что заданный предмет имеет элемент, который на гори
зонтальную плоскость проекций проецируется в виде шестиугольника, а на фронтальную — в виде прямоугольника. Такое изображение имеет призма, ось которой перпендикулярна горизонтальной плоскости проекций.
Внутри цилиндра диаметром 48мм имеются два паза, ширина которых 24мм.,а высота 10мм.
Выявив поверхности, ограничивающие заданный предмет, можно мысленно расчленить его на ряд элементов:
основание, представляющее собой четырехугольную призму, в которой имеется сквозной паз шириной 40мм. и высотой 6мм., четыре цилиндрических отверстия диаметром 18мм.,а также размещено ушко длиной 30мм., шириной 10мм. с выполненным в нём сквозным цилиндрическим отверстием диаметром 20 мм;
расположенный на основании цилиндр диаметром 48мм. с внутренним шестиугольным отверстием и двумя пазами шириной24мм., высотой 10мм.
Мысленно расчленив (прочитав) таким образом предмет, можно приступать к построению в тонких линиях недостающих его изображений, которое следует производить по элементам.
В приведенном примере имеется хорошая возможность соединять виды с соответствующими разрезами, и одновременно строить разрезы, выявляющие невидимые контуры скрытых элементов (рис. 2.119).
Скрытыми элементами здесь являются: центральное шестиугольноеотверстие в цилиндре, четыре цилиндрических отверстия в основании и одно цилиндрическое отверстие в ушке.
Выявление этих элементов производится с помощью ступенчатого разреза А-А на главном виде и простого разреза на виде слева, выполненного плоскостью, совпадающей с плоскостью симметрии детали. Разграничение вида и разреза на главном виде волнистой линией обусловлено наличием ребра призматического отверстия, проекция которого совпадает с осью изображения, а на виде слева-несимметрией изображения.
Размеры на чертеже проставляются в соответствии с правилами, описанными в разделе 2.4.
2.8 Построение проекций и натурального вида фигуры сечения детали проецирующей плоскостью
Проецирующие плоскости не параллельные ни одной из плоскостей проекций пересекают деталь по фигуре, проекции которой не являются натуральным видом этой фигуры. Необходимо уметь строить эти проекции, а по ним и натуральные виды фигур сечений. Такая задача решается в следующей последовательности.
Проецирование точки в начертательной геометрии с примерами
Проецирование точки на две и три плоскости проекций:
Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций
Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки А:
Плоскость прямоугольника 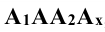
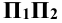
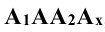
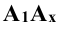
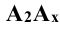
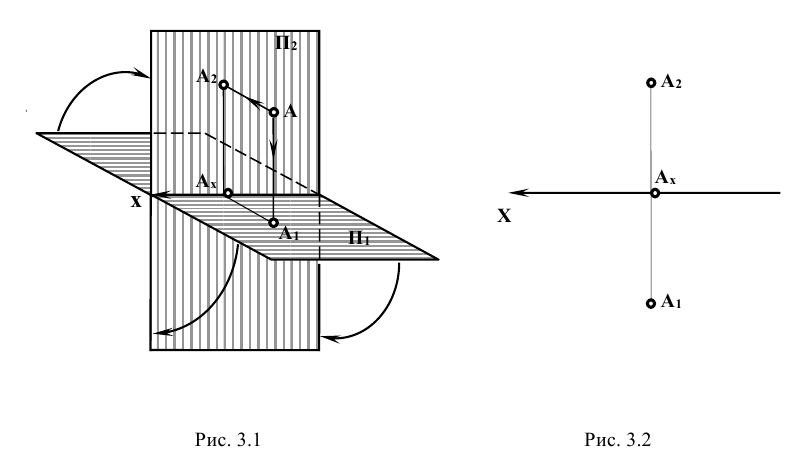
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость 
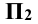
Проекции 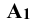
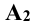
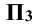
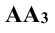
Для получения плоского чертежа в этом случае уже две плоскости 
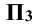
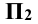
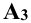
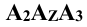
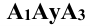
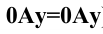
Это не означает, что модули этих величин обязательно равны между собой, т.е. 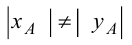
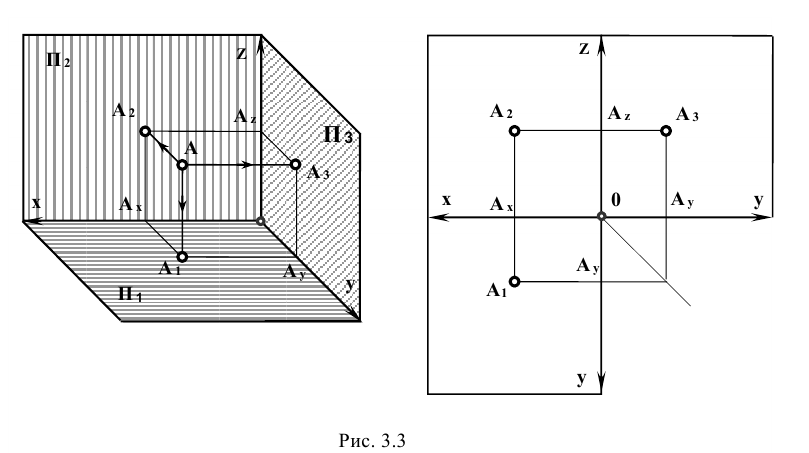
Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например А, принадлежит:
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А принадлежит:
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Так, точка А лежит на оси х, если 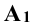
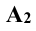
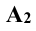
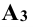
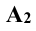
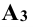
Правила знаков координат проекции точки
При построении проекции точки координата x всегда откладывается от начала координат (точка 0).
Таблица 3.1
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.