Как построить квадрат вписанный в окружность

Техническое черчение

Popular

Основы черчения

Строительное

Машиностроительное

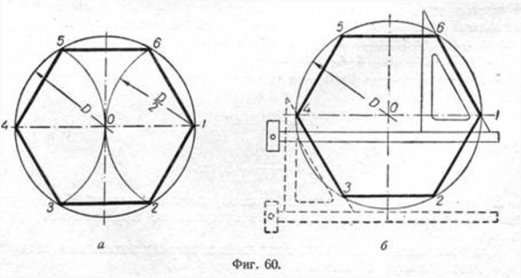
Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

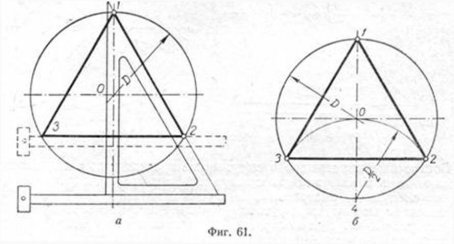
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

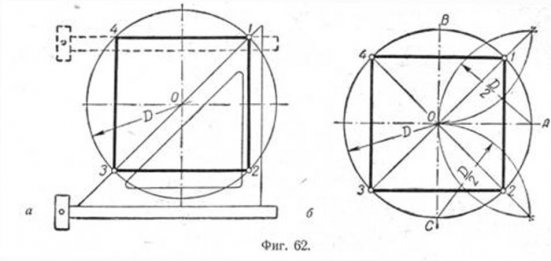
Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

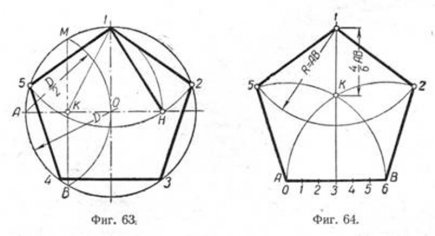
Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

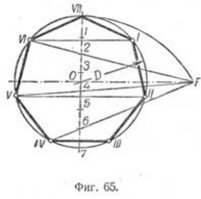
Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

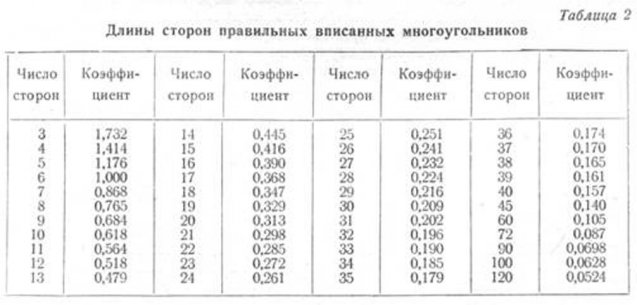
Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Источник

Соответствие круга и квадрата в перспективе.

Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометричес­кая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в лю­бой квадрат можно вписать окружность.

Как вписать окружность в квадрат?

Горизонтальный квадрат.

Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и ухо­дящие с ними в одну точку схода.

перспективный рисунок простых геометрических тел

Вертикальный квадрат.

Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигу­ры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспекти­ве, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.

Источник

Геометрия как искусство: 4 и 8 (часть третья)

Эта статья — продолжение цикла переводов, посвященных геометрии и тому, как она работает в искусстве. О том, чем рисовать и как читать схемы, можно прочитать в предыдущих частях (инструменты и базовые построения).

Прим.пер. — Если кому-то неинтересно возиться с карандашом и циркулем, в комментариях к оригиналу подсказывают, что с построениями можно попробовать поиграть в Adobe Illustrator. С точки зрения практической реализации я не советчик, но идея симпатичная. Дерзайте)

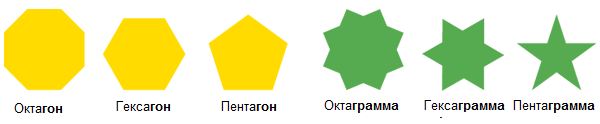
Сегодня разбираемся с геометрией чисел 4 и 8, то есть строим квадраты, октагоны, октаграммы и несколько узоров, на них основанных. Но для начала определимся с терминами:

Если для каждого числа сторон существует единственный правильный выпуклый многоугольник, то звездчатых, наоборот, будет несколько, в зависимости от того, как соединяются точки. Чем больше лучей, тем больше вариантов. (прим. пер. – Вообще, кому интересно, на википедии написано чуть подробнее, и есть понятная картинка)

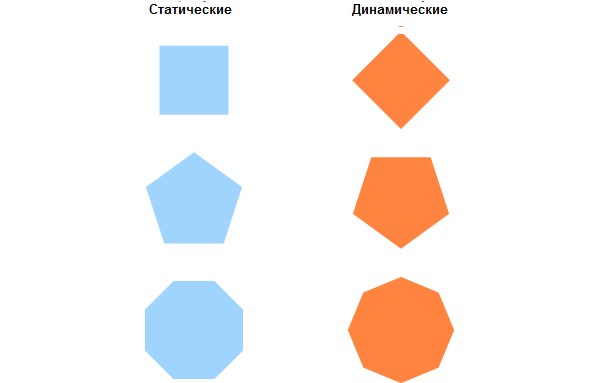
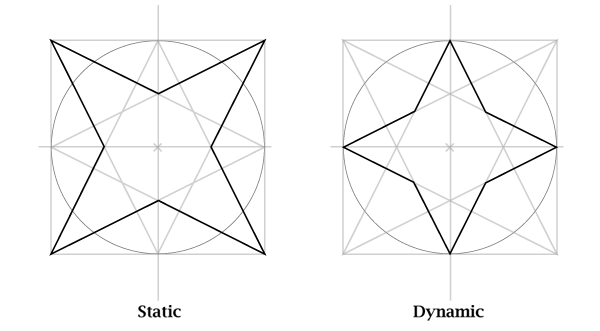
Еще два понятие, которые мы часто будем использовать для описания фигур – статическая и динамическая. Статическая лежит на своей стороне, динамическая – опирается на угол.

Эти определения довольно точно выражают чувства, которые вызывают эти фигуры. (Да, геометрия и чувства в одном предложении, вы не ослышались.)

При построении любой фигуры мы должны сперва решить, будет ли она статической или динамической, так как от этого будет зависеть выбор метода построения. И не только от этого: мы далеко не всегда начинаем с нуля, часто нужно вписаться в имеющиеся построения, начать с заданной точки, сегмента, окружности, соотношения. Каждая из этих ситуаций требует особого подхода.

Я не буду рассматривать все, потому что тысячи их, но покажу как минимум по паре для каждой фигуры, чтобы вы попробовали строить всякие штуки по-разному.

Фигуры

Квадрат (лежащий на одной из сторон)

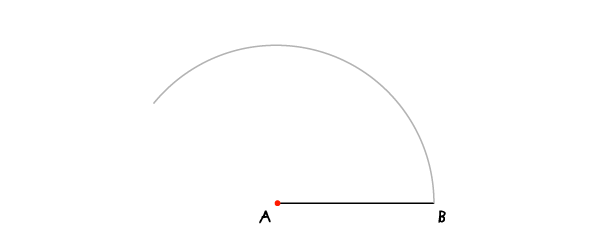
В соответствии с заголовком этот метод используется, когда одна из сторон квадрата задана или когда вам надо с чего-то начать (в этом случае до Шага 1 проведите сторону, на которой будете строить свой квадрат).

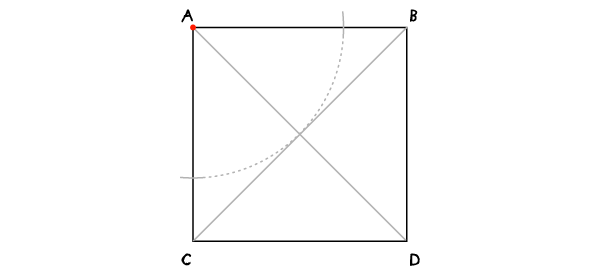
Шаг 1

С раскрывом циркуля на АВ проведите дугу с центром в А. Во всех дальнейших построениях раскрыв циркуля останется неизменным.

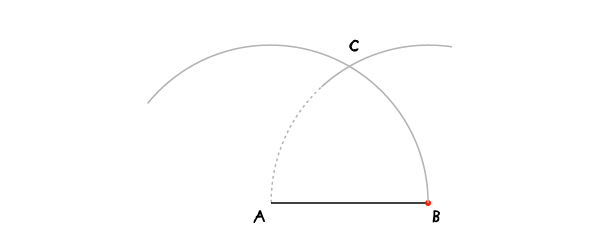
Шаг 2

Переместите иглу в точку В и проведите дугу, пересекающую первую в точке С.

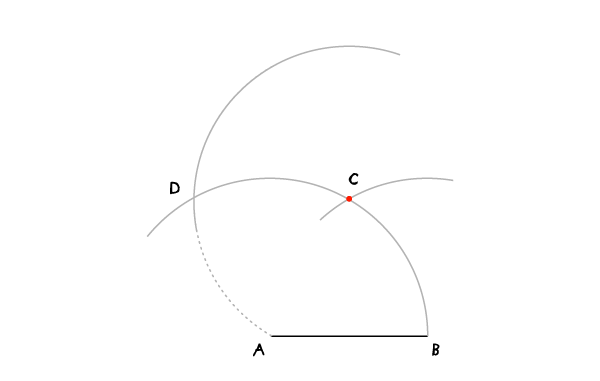
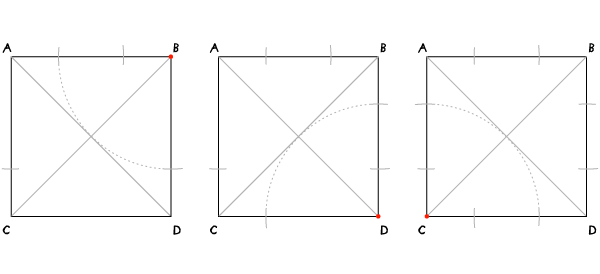
Шаг 3

Переместите иглу в точку С и проведите дугу, также пересекающую первую (с центром в А) в точке D.

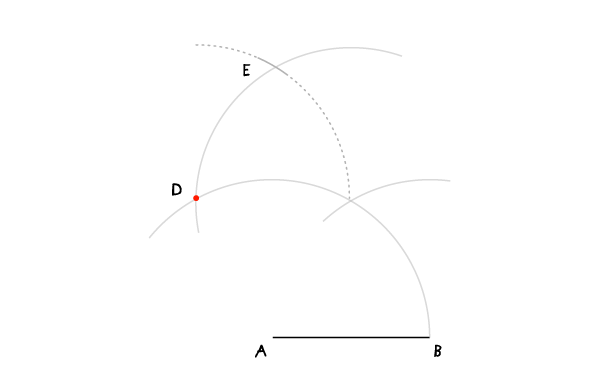
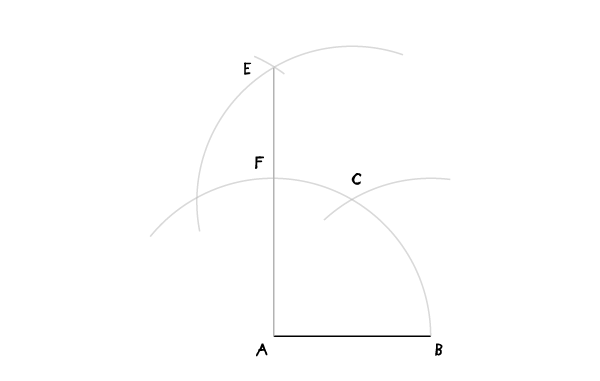
Шаг 4

Переместите иглу в D и проведите дугу, пересекающую проведенную в шаге 3 в точке E.

Шаг 5

Соедините Е и А, чтобы найти F. В это мы проделали для того, чтобы найти перпендикуляр к АВ через точку А.

Шаг 6

Последняя дуга: поместите иглу в точку F и проведите дугу, чтобы найти точку G. Эту дуга будет пересекать дугу с центром в В.

Шаг 7

Соедините G, Fи B, чтобы закончить построение квадрата.

Хотя описанный метод и полезен, я заметила, что традиционно в искусстве отдают предпочтение другому, тому, где построение начинается от заданной окружности. Возможно, это дань символизму, напоминание о Единице (символ которой – окружность), начале всех начал, а возможно, он просто более ясный.

Однако, совсем отказываться от предыдущего метода не стоит. Если все, что у вас есть, это древнющий ржавый циркуль, раскрыв которого раз и навсегда установил еще ваш прадедушка, то следующий метод вам не подойдет.

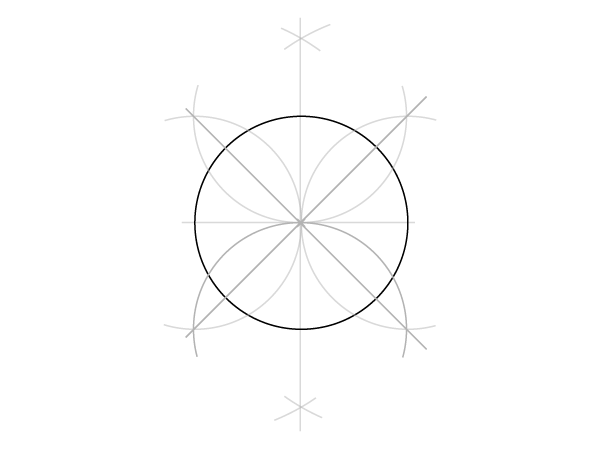
Динамичный квадрат (вписанный в окружность)

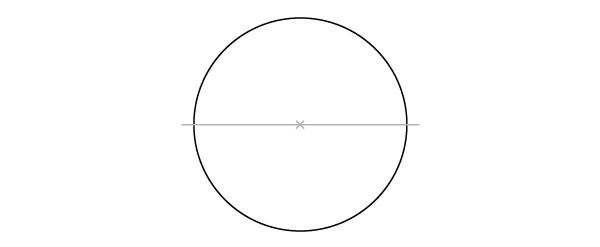
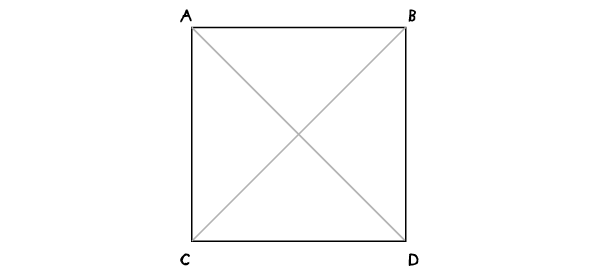
Наша отправная точка– окружность с одним проведенным диаметром. Начали вы с диаметра или с окружности – неважно.

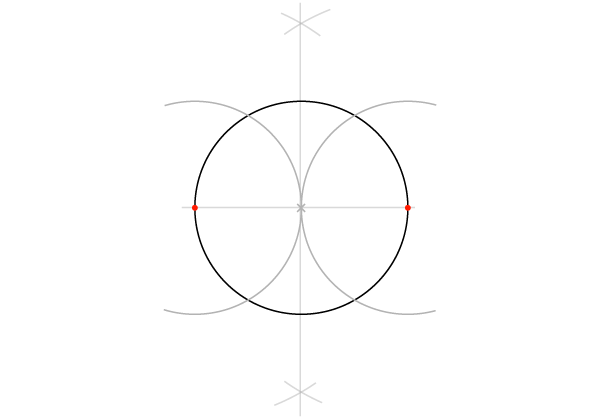
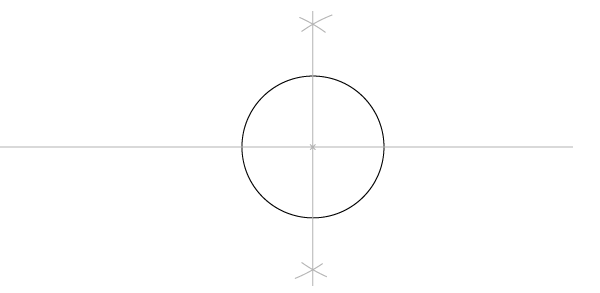
Шаг 1

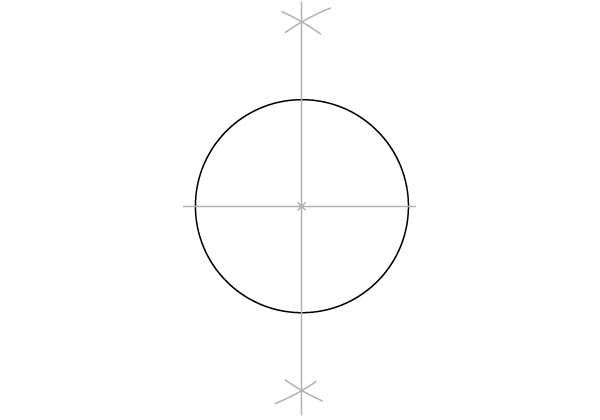
Постройте перпендикуляр к диаметру, делящий его пополам, как во второй части(ссылка). Начните с рисования двух пересекающихся дуг…

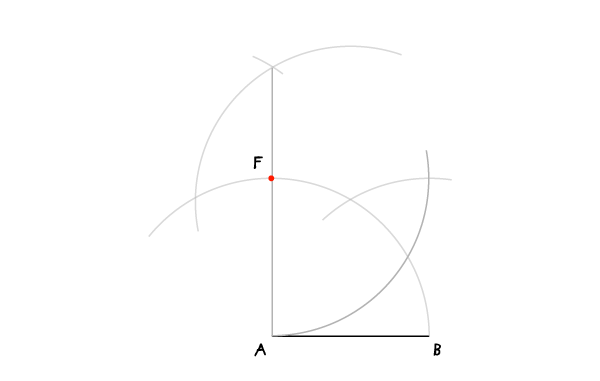
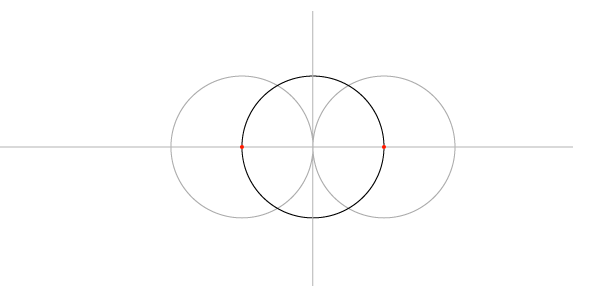
Шаг 2

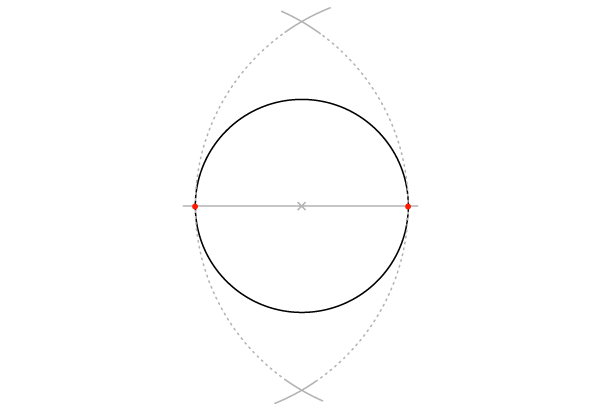
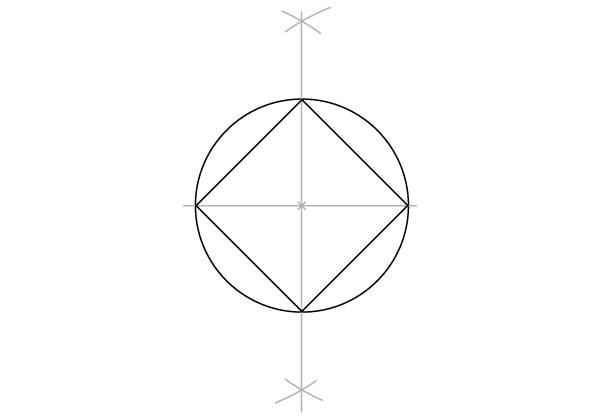
… и соедините две точки пересечения. Перпендикуляр пересечет окружность в двух точках, и мы таким образом получим 4 определенные точки на окружности.

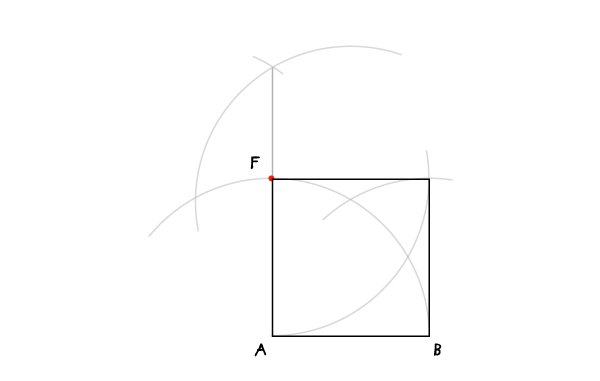
Шаг 3

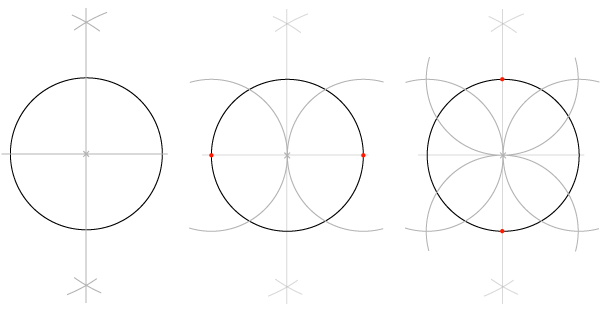
Статический квадрат (на основе вписанной окружности)

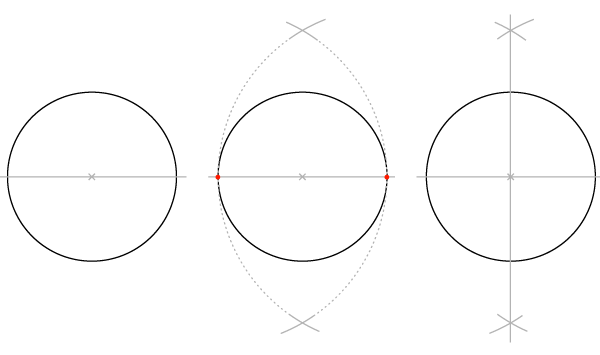
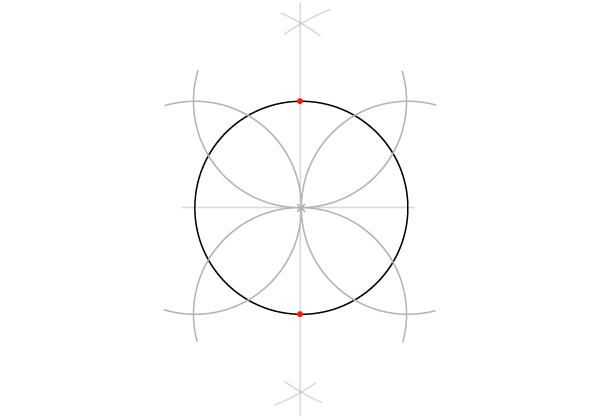
Шаги 1-2

Те же, что в прошлый раз: начинаем с круга с горизонтальным диаметром, ищем перпендикуляр так, чтобы окружность оказалась разделена на 4 части.

Шаг 3

Устанавливаем раскрыв циркуля равным радиусу и проводим две дуги с центрами в двух начальных точках. Точкой соприкосновения дуг окажется центр окружности.

Шаг 4

Повторяем то же для двух точек, полученных после построения перпендикуляра. Эти 4 дуги определяют 4 точки, лежащие вне окржности.

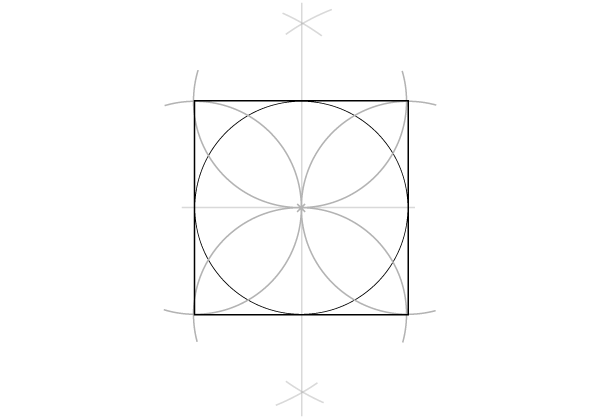
Шаг 5

Теперь только два шага отделяют нас от того, чтобы получить две четырехконечные звезды.

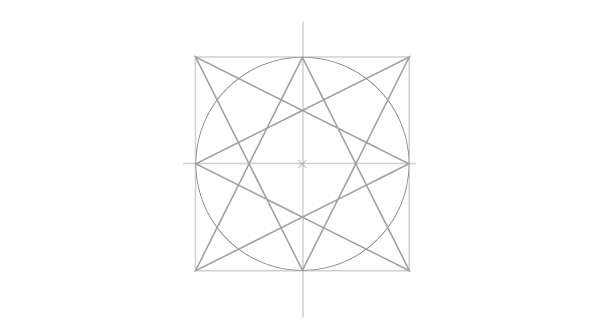
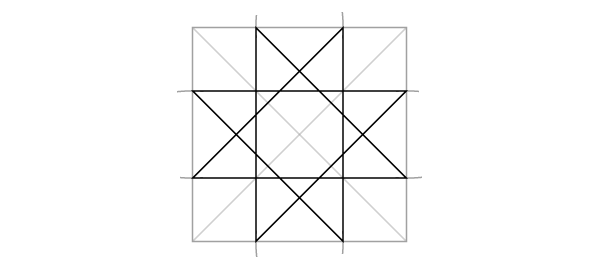
Статическая и динамическая четырехконечные звезды

Шаг 6

Соедините 4 точки, лежащие на окружности с 4 углами статического квадрата, как показано на рисунке:

Шаг 7

Обведите нужную вам звезду.

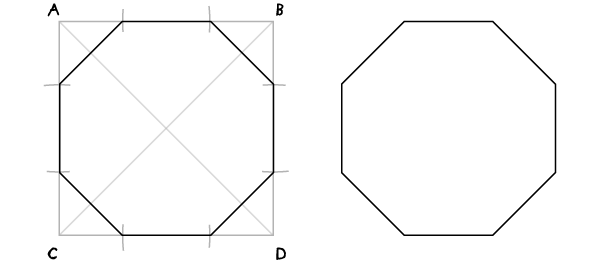
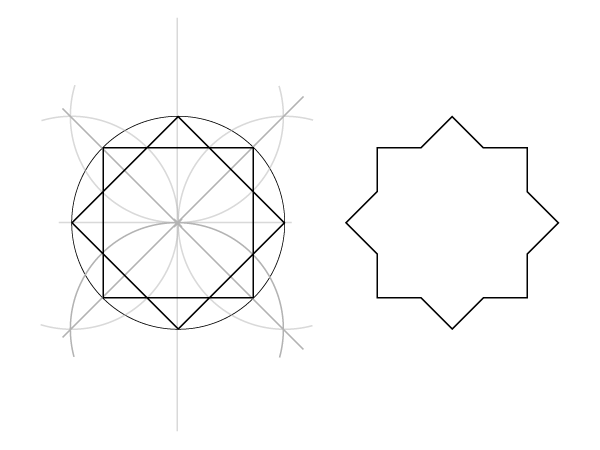
Статические октагон и октаграмма (вписанные в квадрат)

Шаг 1

Начните с квадрата, проведите диагонали.

Шаг 2

Установите иглу в А и с раскрывом циркуля от А до центра квадрата найдите две точки на сторонах квадрата.

Шаги 3-5

Повторите шаг 2 для точек В, С и D.

Шаг 6

Для октагона: соедините восемь найденных точек.

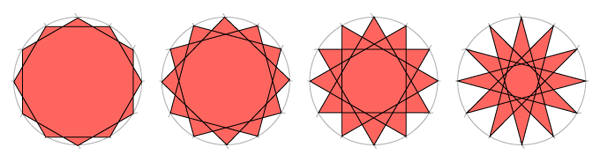
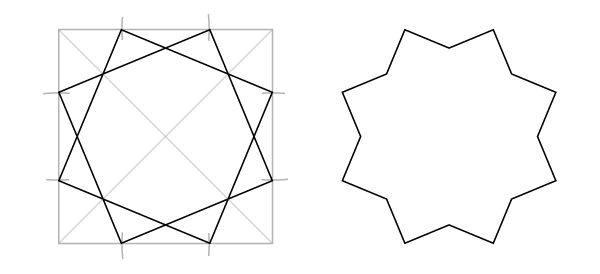
Для октаграммы соедините точки как показан на рисунке. Получится, что вы соединяете точки через одну. Обратите, что классическая октаграмма образована при взаимном повороте двух квадратов.

Еще одну октаграмму можно получить, если пропускать точки через две.

Обратите внимание, что меньшая октаграмма точно вписывается в большую.

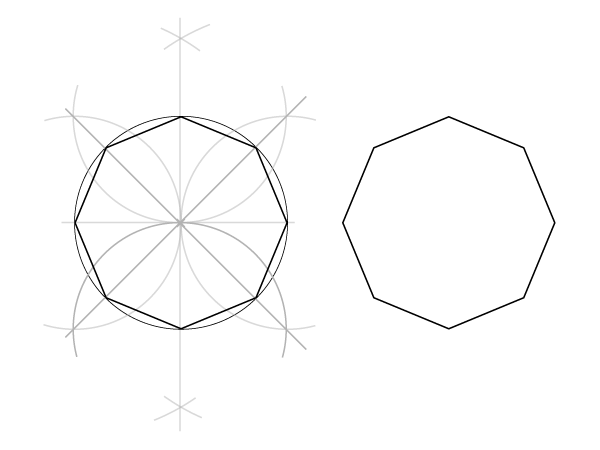
Динамичный октагон (вписанный в круг)

Шаги 1-4

Такие же, как при построении статического октагона. Остановитесь до момента, когда нужно соединять точки.

Шаг 5

Соедините внешние точки по диагонали. Диагонали пересекут окружность в новых 4 точках, то есть теперь она разбита на 8 частей.

Шаг 6

Для динамичного октагона соедините эти 8 точек.

Для динамичной октаграммы соедините точки через одну, как показано ниже, нарисовав два квадрата.

плитки из центрального Ирана, XIV век

Узоры

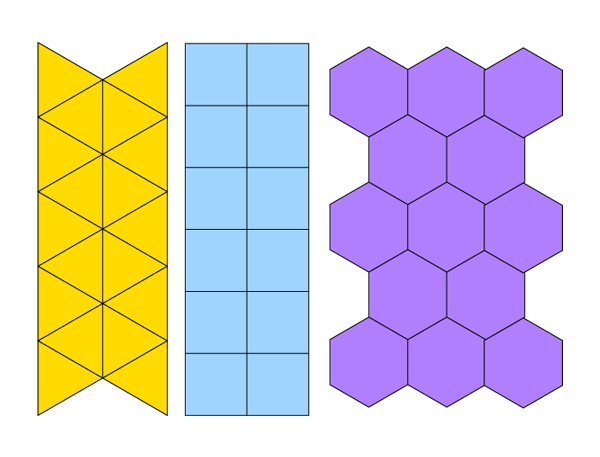
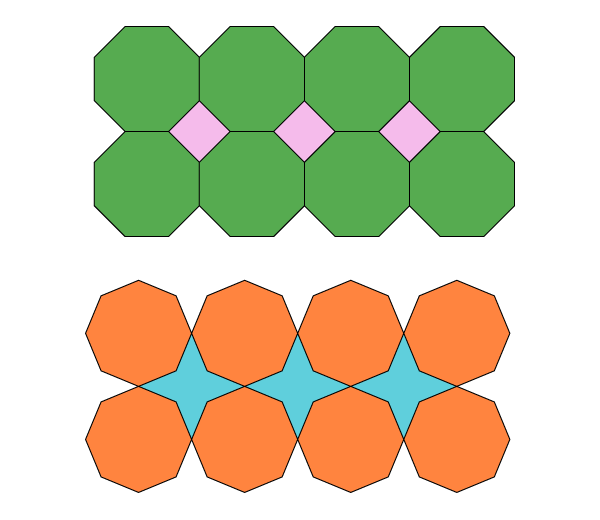
До настоящего момента мы строили только отдельные фигуры, теперь у нас достаточно знаний, чтобы начать складывать из этих фигур мозаичные узоры. Что еще нужно знать перед началом работы с мозаикой: только квадраты, а также равносторонние треугольники и шестиугольники складываются друг с другом, не оставляя между собой пустот.

Все прочие, включая октагоны, приведут к появлению промежутков различной формы. Это является недостатком, например, при выборе формы упаковки, поскольку при перевозке проявляется нерациональное использование пространства. В случае с искусством никакой это не недостаток: небольшие пространства работают в противовес крупным формам, позволяя создать контраст по цвету и размеру, или, наоборот, в слиянии получить новые необычные формы.

Но вернемся к нашему упражнению. С использованием восьмиугольных форм можно получить три различных простых узора на основе общей базовой структуры. Структура эта основана на четырех окружностях вокруг пятой, а, следовательно, образует сетку из квадратов, которая также носит название сетки пяти окружностей. Позвольте заметить, на случай если вам попадется термин, что структуры (сетки) на основе квадратов также носят название √2-сетки. Все эти термины значат, что мы работаем с числами 4 и 8 (и 12, и 16, и далее по мере прибавления 4).

При построении сетки невозможно переоценить важность очень точной работы, особенно теперь, когда от фигур мы переходим к узорам. Убедитесь, что карандаш как следует заточен и не спешите.

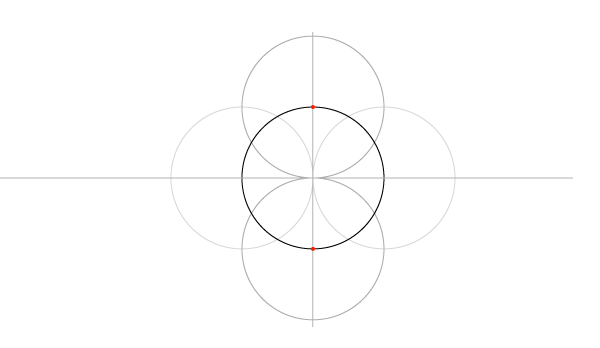
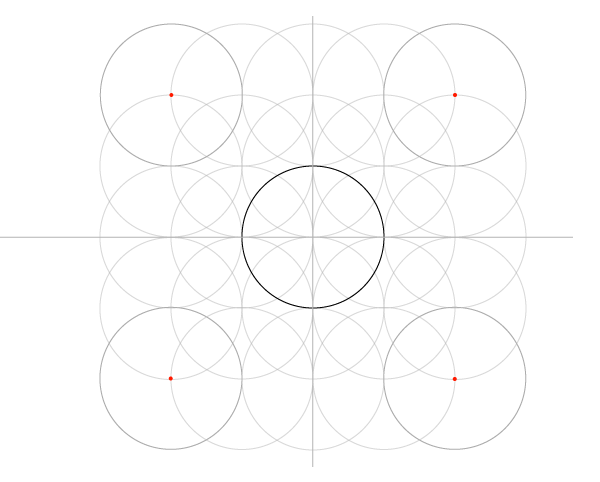
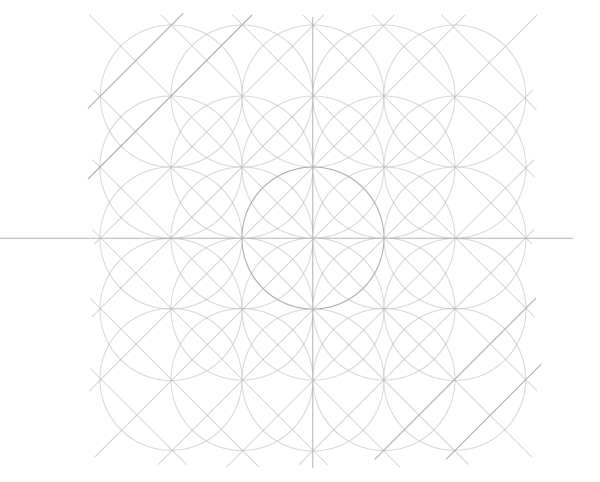
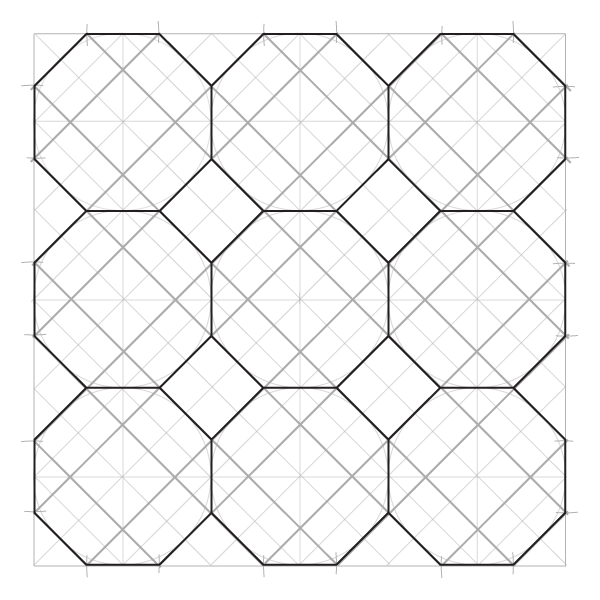
Сетка пяти окружностей

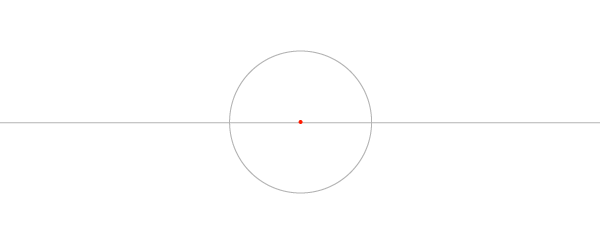
Шаг 1

Нарисуйте отрезок по горизонтали и окружность, центр которой лежит на этом отрезке, имея ввиду, что стороны квадратов в сетке равны диаметрам окружностей, и эта первая окружность будет центром сетки.

Шаг 2

Найдитеипостройтеперпендикуляр. Он должен быть как минимум равен отрезку, но может быть и длиннее.

Шаги 3 и 4

Следующий шаг – знакомые нам дуги, только в этот раз рисуйте полные окружности. В итоге у нас должна получиться основа основ: пять окружностей, которые дали сетке имя.

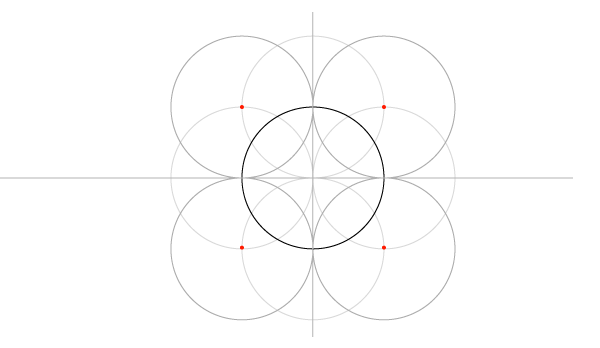
Шаг 5

Постройте еще 4 окружности с указанными на рисунке центрами…

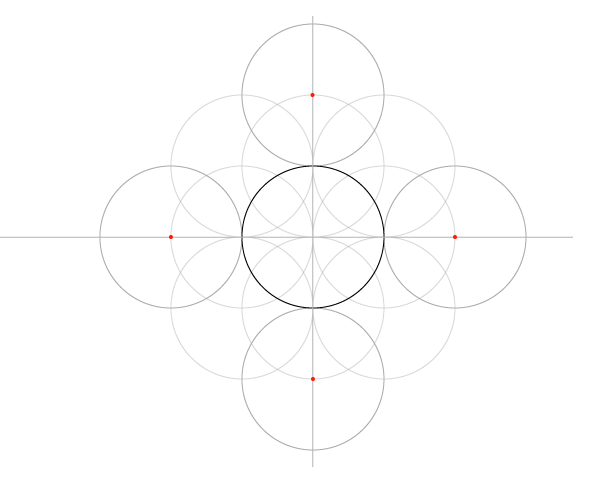
Шаг 6

Шаг 7

И еще восемь с центрами, указанными на рисунке ниже. Обратите внимание, что центры новых окружностей окажутся в точках пересечения предыдущих. Таким образом структуру можно расширять до бесконечности, но мы пока добавим только еще один блок.

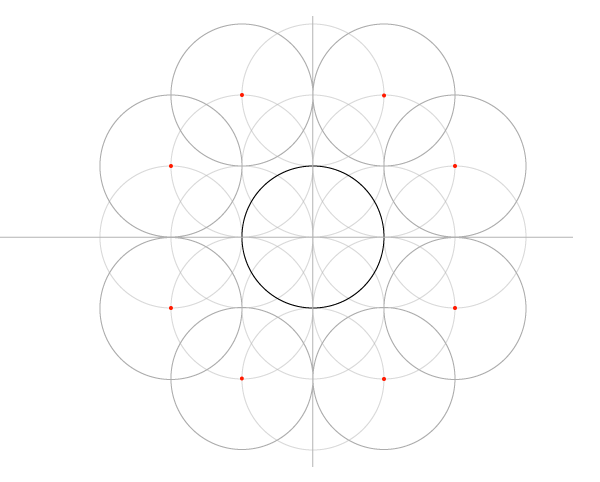
Шаг 8

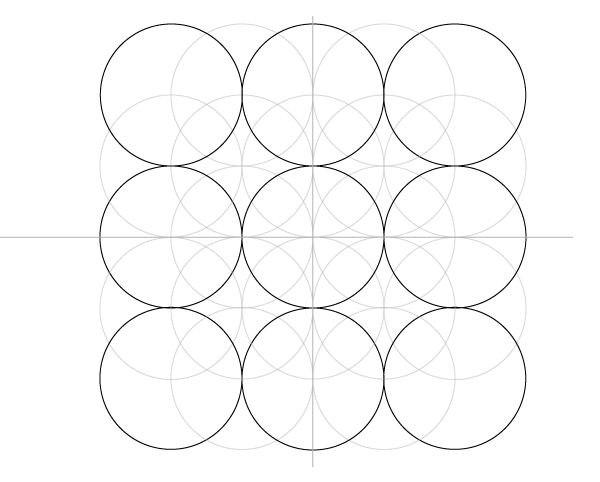
Впишите стеку в квадрат, добавив окружности по углам.

Теперь у нас есть 25 окружностей, но большинство было нужно только чтобы построить сетку. Для начала работы над узором нам понадобится только 9 соприкасающихся окружностей, вписанные в соответствующие квадраты.

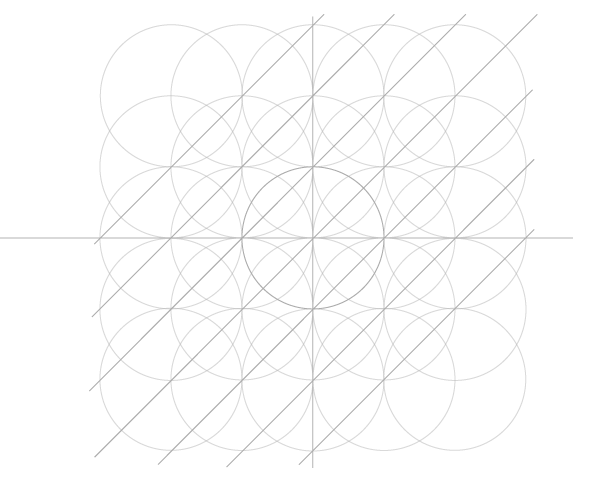
Шаг 9

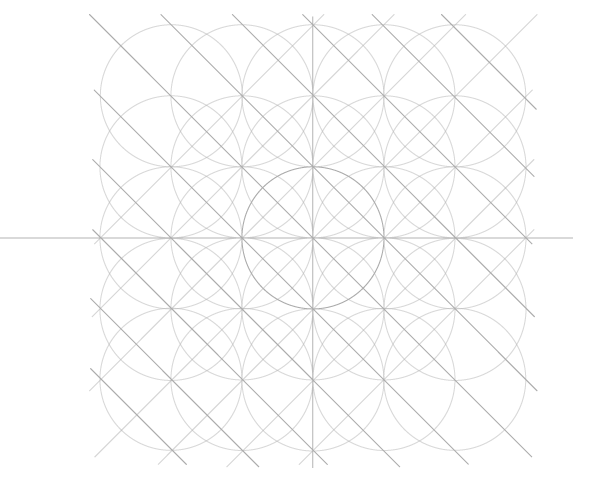
Последний шаг в построении сетки – добавить диагонали. Углов у окружностей нет, но есть точки соприкосновения. Их и соединяем, сначала в одну сторону…

Добавляем недостающие соединением точек пересечения уже построенных диагоналей с окружностями по углам сетки.

Теперь перед нами сетка, которая ляжет в основу всех следующих построений. Можно еще построить квадрат, в который впишется сетка целиком, но это необязательно.

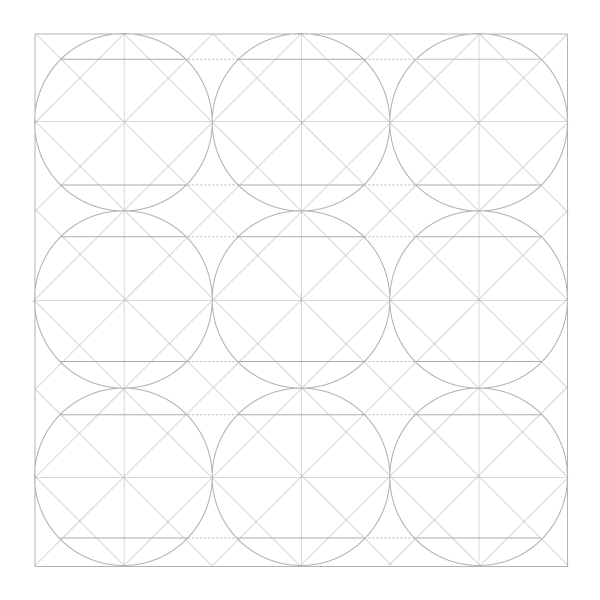
Узор из динамичных октагонов

Дополнительные построения не требуются: каждая окружность уже разделена на 8. Все, что от вас требуется, — соединить точки в каждой окружности.

Узорчатый пол в гробнице Итмад-Уд-Даулы, фото Дэвида Кастора (David Castor)

Дыхание милостивого

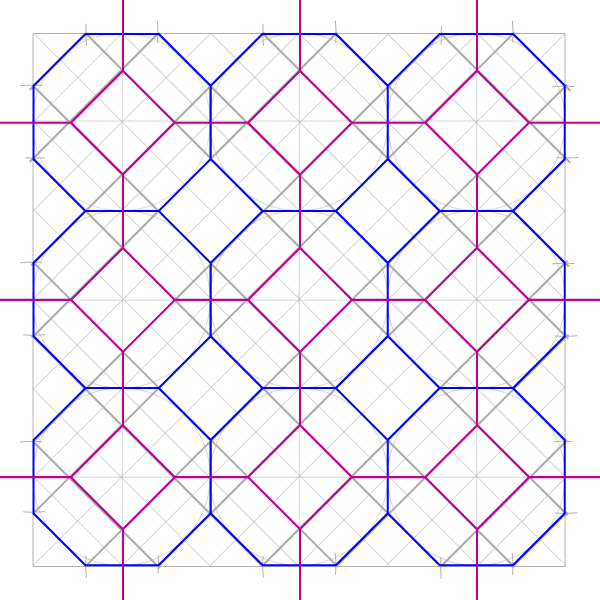
Это поэтическое название принадлежит узору, в котором октаграммы прилежат друг к другу, образуя крестообразные пустоты. Отправная точка снова сетка пяти окружностей.

Шаг 1

Динамичные квадраты уже есть – они образованы диагоналями. Добавляем горизонтальные стороны вторых квадратов…

Шаг 2

Шаг 3

Теперь обводим звезду, образованную наложением квадратов.

В том, что получилось, можно увидеть, откуда появилось название узора: октаграммы – “выдыхающие” квадраты (они расшираются), кресты – “вдыхающие” (они сжимаются).

Плитки из узора (развернутого на 45º), найденные в Иране, фотограф ean-Pierre Dalbéra.

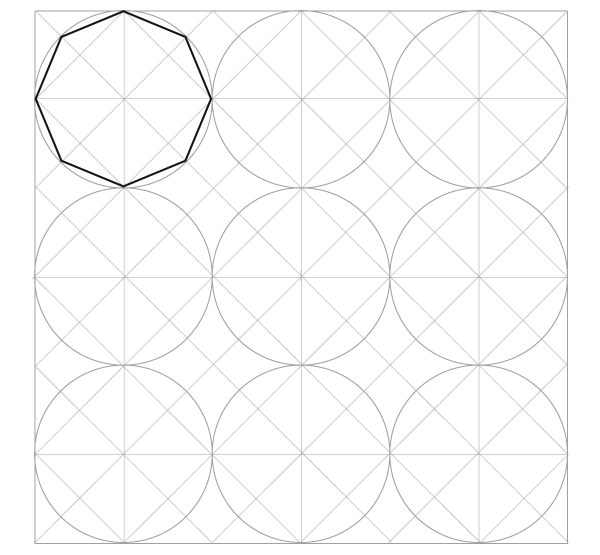
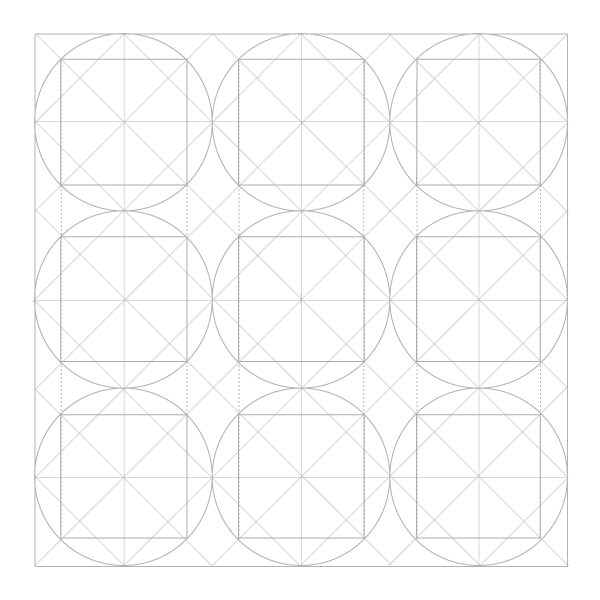
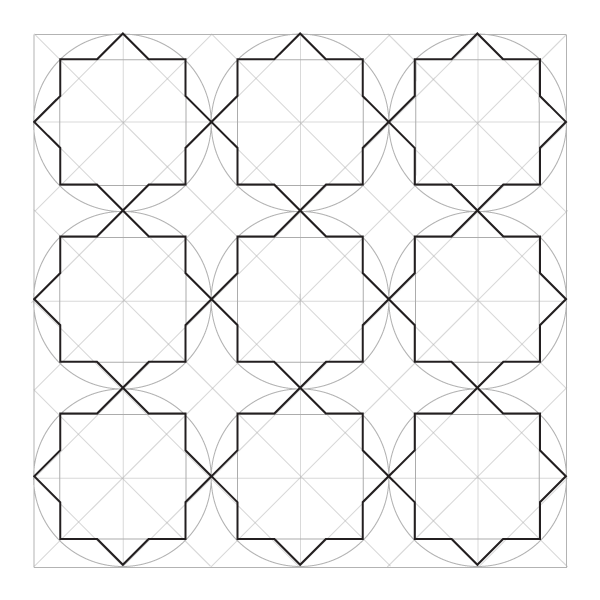
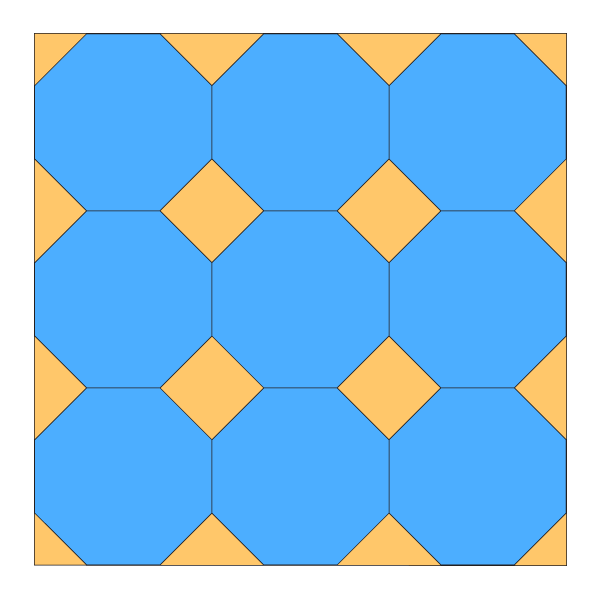
Узор из статичных октагонов

Этот узор основан на статичных октагонах, которые мы уже научились строить немного раньше. Осталось только привязать наше умение к сетке. К счастью, нам нужно построить только самые удаленные от центра точки, все остальное сойдется само.

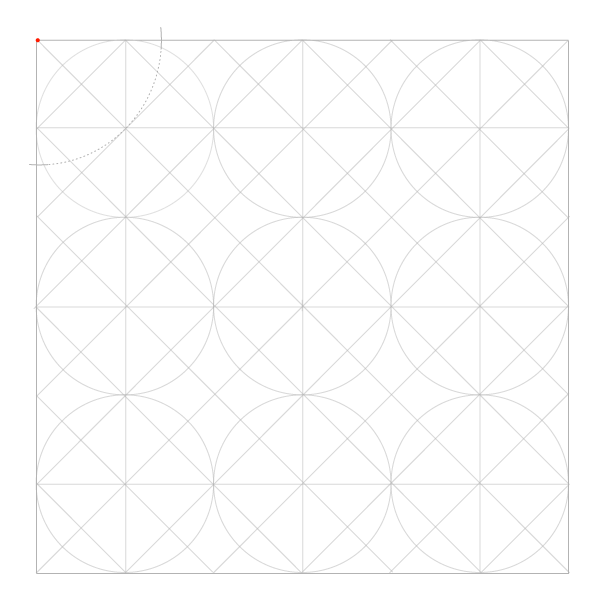
Шаг 1

Иглу циркуля устанавливаем в вершину внешнего квадрата и берем раскрыв, равный расстоянию от этой точки до центра ближайшей угловой окружности. Отмечаем на сторонах квадрата две точки.

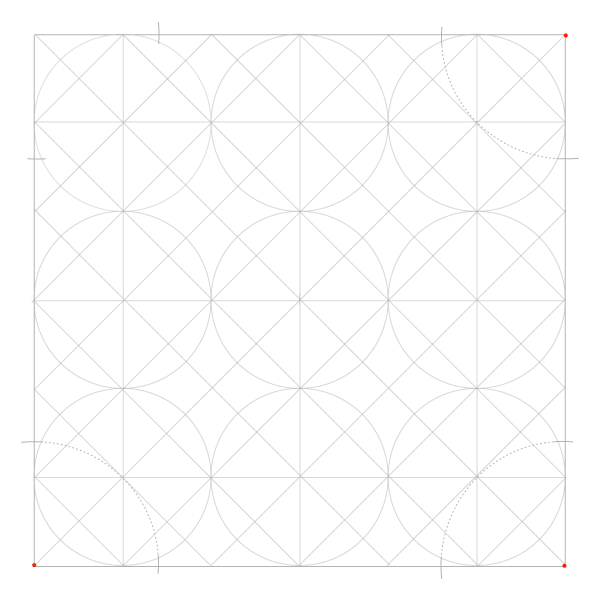
Повторяем аналогичные построения для всех угловых окружностей и получаем еще 6 точек.

Продолжаем построения с иглой циркуля во внешних вершинах квадратов, образованных диагоналями.

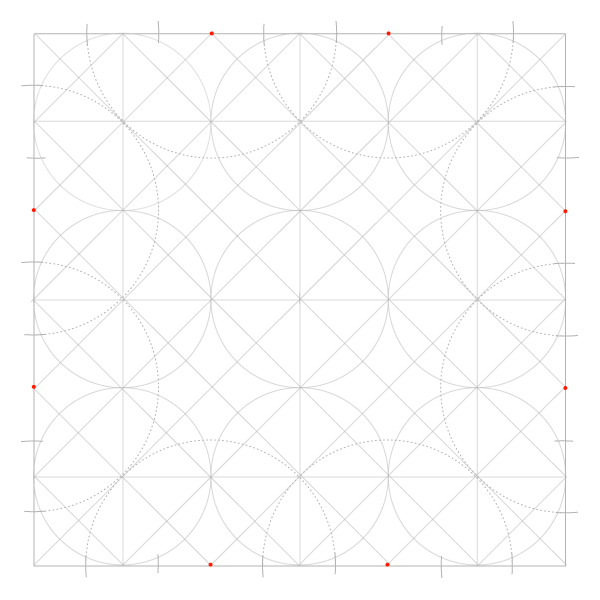
Использование более мягкого карандаша позволит вам лучше понять, как новые линии ложатся на имеющуюся сетку: соедините им периферийные точки, которые вы только что наметили. Это новая сетка с новыми пересечениями.

Соедините эти пересечения, чтобы получить восьмиугольники, лежащие на одной стороне.

И напоследок: вот какой узор получится, если вы соедините лини, по которым октагоны накладываются друг на друга:

На сегодня все. Оперируя только числами 4 и 8 мы научились строить квадраты и октагоны, а также четырех- и восьмиконечные звезды, структуру на основе квадратов и 4 узора на основе этой структуры (а их можно придумать гораздо больше, чем 4).

В следующий раз все то же самое проделываем с числами 6 и 12.

Источник