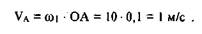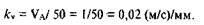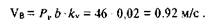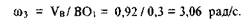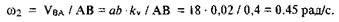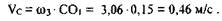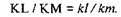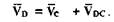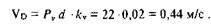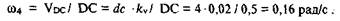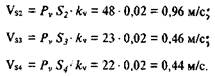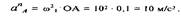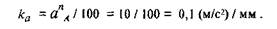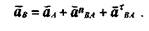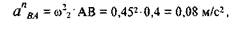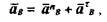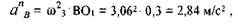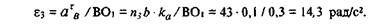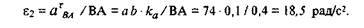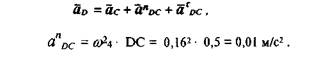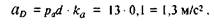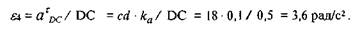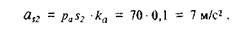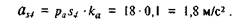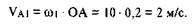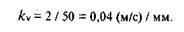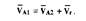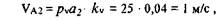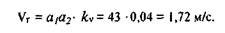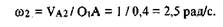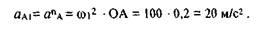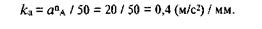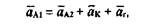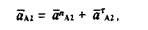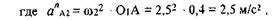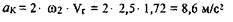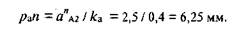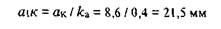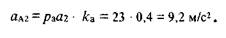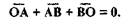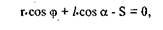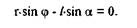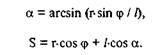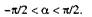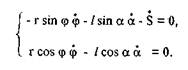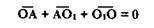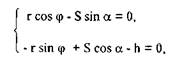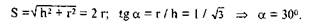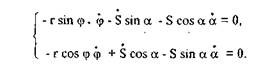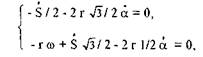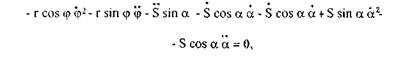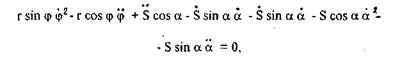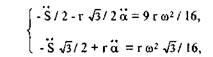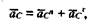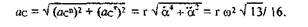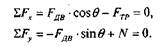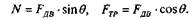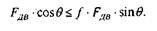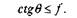Как построить крайние положения механизмов

Определение крайних положений механизма

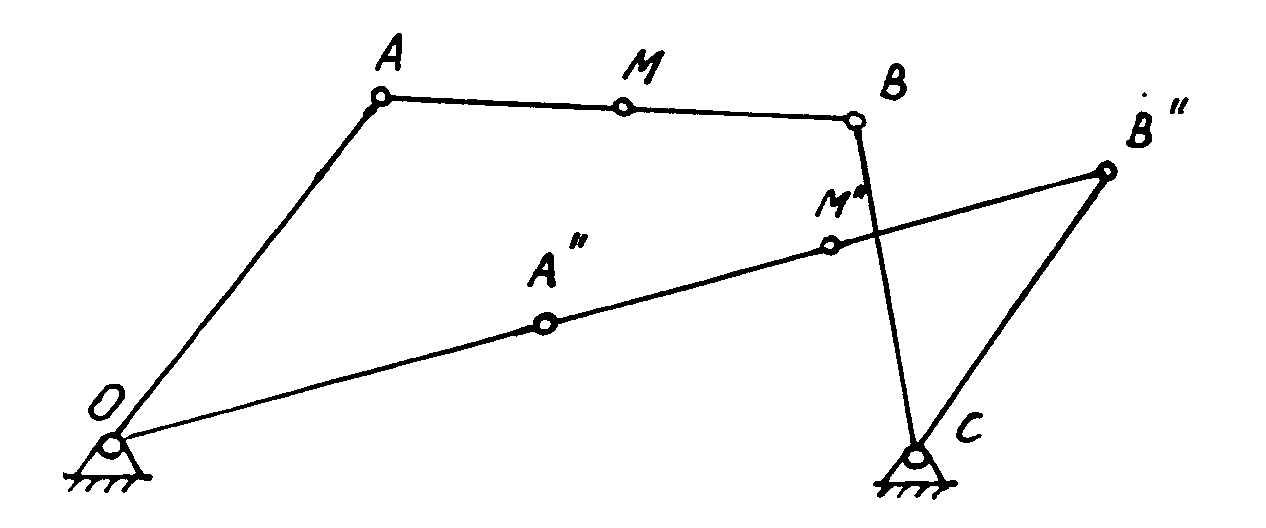
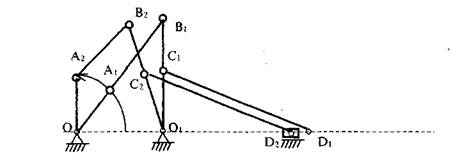
Возьмем шарнирный четырехзвенник.

Ведущее звено (кривошип) может совершать полный оборот 360 0 радиусом ОА с центром т.О.

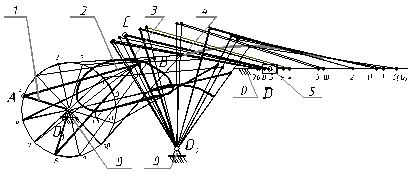
На шатуне АВ выбираем произвольную точку М. Окружность I делим на 12 равных частей. Через каждые 30 0 делаем засечки на окружности. В соответствии с размерами звеньев строим положения (все 12) для всех остальных звеньев. На каждом шатуне А_п В_п отмечаем положение т.М. в соответствии с расстоянием АМ. Затем соединим все положения точки М плавной кривой, получим траекторию этой точки. Мы здесь заметили, что коромысло ВС не делает полного оборота, как кривошип ОА, оно поворачивается между двумя крайними точками. Эти крайние (мертвые) положения определяются следующим образом. Для нашего четырехзвенника это будет нетрудно. Очевидно, что звено ВС достигнет правого крайнего положения в случае, когда кривошип ОА и шатун АВ вытянутся в одну линию.

Нахождение крайних положений коромысла ВС

Обозначим ОА=r , АВ=L

Сделаем засечку на дуге окружности радиусом, равным длине звена ВС, проведя дугу радиусом R=r+L из центра О. Полученную точку В» соединяем с точкой С.

Отрезок В»С и есть крайнее правое положение механизма. Соединяя В» с точкой 0 получим соответствующие положения ОА» и А»В».

Крайнее левое положение механизма получим тогда, когда кривошип и шатун сложатся в одну линию. Для этого делаем засечку на траектории точки В радиусом R=L-r из центра 0. Соединим В’ с точкой С получим левое крайнее положение коромысла В’С. Проведя прямую В’0 получим положение шатуна А’В’ и кривошип А’0. Угол

Источник

Крайние положения механизма

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ «МАМИ»

Кафедра «Теория механизмов и машин»

КИНЕМАТИЧЕСКИЙ И СИЛОВОЙ РАСЧЕТ МЕХАНИЗМА

Методические указания к курсовому проектированию по теории

механизмов и машин

1. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА………………………. 3

2. ПОСТРОЕНИЕ ПОЛОЖЕНИЙ МЕХАНИЗМА…………………… 4

2.1. Крайние положения механизма………………………………… 4

2.2. Выбор положений механизма, соответствующих рабочему

и холостому ходу, и определение внешней силы

Для механизмов станков и прессов……………………….. 6

Для механизмов компрессоров……………………………. 8

Для механизмов двигателей внутреннего сгорания……… 9

3. ПОСТРОЕНИЕ ПЛАНОВ СКОРОСТЕЙ И УСКОРЕНИЙ………… 11

4. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ МЕХАНИЗМА……………… 19

4.1. Определение сил инерции звеньев………………………………. 19

4.2. Определение реакций в кинематических парах и

уравновешивающей силы……………………………………… 21

5. ОПРЕДЕЛЕНИЕ УРАВНОВЕШИВАЮЩЕЙ СИЛЫ

С ПОМОЩЬЮ РЫЧАГА ЖУКОВСКОГО…………………………… 27

6. ПРИМЕР КИНЕМАТИЧЕСКОГО И КИНЕТОСТАТИЧЕСКОГО

ИССЛЕДОВАНИЯ МЕХАНИЗМА…………………………………… 27

6.1. Структурный анализ механизма………………………………… 29

6.2. Построение положений механизма……………………………… 30

6.3. Построение планов скоростей и ускорений…………………… 30

6.4. Кинетостатический расчет механизма…………………………….35

6.4.1. Определение сил инерции звеньев…………………………. 35

6.4.2. Определение реакций в кинематических парах

и уравновешивающей силы…………………………………. 36

6.5. Определение уравновешивающей силы с помощью

В настоящих методических указаниях рассматривается решение задач кинематического анализа и силового расчета плоских рычажных механизмов.

Задачи кинематического анализа: определение положений механизма по заданному положению начального звена (за начальное звено во всех механизмах, данных в заданиях на курсовой проект, принимаем кривошип); определение скоростей и ускорений характерных точек механизма по заданной скорости и ускорению начального звена. Кинематический анализ проводим графическими методами: положения звеньев механизма определяем методом засечек; скорости и ускорения различных точек звеньев определяем методом построения планов скоростей и ускорений.

Задачи силового расчета: определение реакций во всех кинематических парах и уравновешивающей силы F_ур (или уравновешивающего момента М_ур) на кривошипе. Силовой расчет выполняем на основе принципа Даламбера, согласно которому в число заданных сил включаем силы инерции и рассматриваем равновесие полученной системы. Такой расчет механизма называется кинетостатическим.

Все исследования проводим, вводя следующие допущения:

1. Считаем, что кривошип вращается равномерно (w₁ = const).

2. Не учитываем трение в кинематических парах.

3. Считаем, что все силы действуют в одной плоскости.

При выполнении листа курсового проекта требуется:

1. Провести структурный анализ механизма.

2. Построить механизм в четырех положениях: два крайних положения, одно положение, соответствующее рабочему ходу выходного звена, и одно положение, соответствующее холостому ходу.

3. Построить планы скоростей и ускорений для трех положений механизма: для положений, соответствующих рабочему и холостому ходу, и для одного из крайних положений.

4. Для положения механизма, соответствующего рабочему ходу, провести кинетостатический расчет:

а) определить силы инерции звеньев,

б) определить реакции во всех кинематических парах и уравновешивающую F _ур силу на кривошипе.

5. Для проверки определить уравновешивающую силу с помощью рычага Жуковского.

Структурный анализ механизма

Методика и порядок кинематического и кинетостатического исследования механизма определяется в результате структурного анализа.

У механизмов с числом степеней свободы W = 1 одно начальное звено.

При кинематическом анализе за начальное звено принимается звено с заданным движением. При кинетостатическом расчете за начальное принимается звено, на котором требуется определить уравновешивающую силу. Во всех механизмах, предлагаемых в заданиях на курсовой проект, задано движение кривошипа и требуется определить уравновешивающую силу на кривошипе. Поэтому за начальное звено для всех схем механизмов принимаем кривошип.

После выделения начального звена и стойки необходимо оставшуюся кинематическую цепь, образованную звеньями механизма, разбить на группы Ассура.

Пример структурного анализа механизма приведен в разделе 6.1.

Дальнейшее исследование механизма проводят по группам Ассура.

Кинематическое исследование начинают с начального звена (кривошипа) и далее рассматривают группы Ассура в порядке присоединения их к начальному звену и стойке.

Кинетостатический расчет начинают с последней присоединенной группы Ассура и заканчивают рассмотрением начального звена (т.е. порядок силового расчета обратен порядку присоединения групп Ассура к начальному звену и стойке).

Построение положений механизма

Крайние положения механизма

Крайним положением механизма называется положение, в котором выходное звено механизма занимает крайнее положение, т.е. положение, из которого оно может двигаться только в одном направлении. Рассмотрим построение крайних положений для некоторых механизмов.

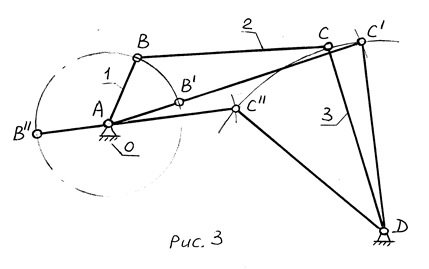
Крайние положения кривошипно-ползунного механизма(рис. 1)

Правое крайнее положение (ПКП) ползун 3 займет, когда кривошип 1 и шатун 2 вытянутся в одну прямую линию (АС¢). При этом точку С¢ получим, делая засечку из точки А радиусом (АВ+ВС) на оси Х-Х направляющих. Точка В кривошипа займет в этом случае положение В¢. Левое крайнее положение (ЛКП) ползун займет, когда шатун с кривошипом совместятся на одной прямой (В²С²). При этом точку С² получим, делая засечку из точки А радиусом (ВС – АВ) на оси Х-Х направляющих. Точка В кривошипа займет соответственно положение В².

В механизмах двигателей внутреннего сгорания (задания 12, 13, 14) крайние положения механизма условно следует определять по правому ползуну. Крайние положения левого ползуна в задании 13 можно не находить.

В большинстве заданий построение выполняется методом засечек. Однако следует иметь в виду, что в некоторых механизмах крайние положения зависят от траектории движения кинематической пары, которой последняя группа Ассура присоединяется к промежуточному механизму.

Так в механизме листоштамповочного пресса (задание № 9) для нахождения крайних положений ведомого ползуна 5 (рис.4) следует построить траекторию центра шарнира С, через который движение передается последующим звеньям. Для этого разбиваем окружности точки В кривошипа на 12 равных частей, начиная деление от произвольного положения точки В. Для каждого из 12 положений кривошипа строим положения звеньев 2 и 3, полученные точки С (1,2,3,…..) соединяем плавной кривой. Крайнее верхнее и крайнее нижнее положения ползуна получим, если отыщем такие точки на оси направляющих Х-Х, которые будут являться центрами дуг радиуса ЕС, касательных к траектории точки С (шатунной кривой) соответственно сверху и снизу, проведенных из точек С¢ и С².

При необходимости таким же методом могут быть найдены крайние положения левого ползуна в задании 13.

Источник

Рычажного механизма

1) Вычертить кинематическую схему механизма для 12 положений ведущего звена, причем за начальное (нулевое) принять такое его положение, при котором выходное звено находится в начале рабочего хода выходного звена (звена, с которым связан инструмент).

2) Построить траектории движения заданной точки К и центров тяжести звеньев. Положение точки К на одном из звеньев механизма задается на практических занятиях преподавателем.

3) Построить диаграмму перемещений ползуна (центр шарнира) рабочего звена за цикл движения механизма. Методом графического дифференцирования построить кинематические диаграммы скоростей и ускорений этой точки и определить масштабы диаграмм. ([4], стр.107-112).

4) Построить планы скоростей для 12 положений механизма. Определить абсолютные скорости шарниров звеньев, центров масс звеньев и заданной точки К. Определить относительные скорости шарниров звеньев и рассчитать угловые скорости звеньев. Полученные значения скоростей точек и угловых скоростей звеньев занести в таблицу.

5) Построить годограф скоростей заданной точки К.

6) Сравнить скорости рабочего ползуна, полученные методом построения планов и методом кинематических диаграмм.Для этого, с помощью масштабов находим значения скорости шарнира рабочего звена на планах и диаграмме, заносим в таблицу и сравниваем их. Максимальная относительная погрешность при сравнении (для инженерных расчётов) не должна превышать 5%.

7) Построить планы ускорений для двух положений механизма при рабочем и холостом ходе рабочего звена (номера положений указываются преподавателем). Определить абсолютные ускорения шарниров звеньев и центров масс звеньев. Определить относительные (нормальные и тангенциальные) ускорения шарниров звеньев и рассчитать угловые ускорения звеньев. Полученные значения занести в таблицу.

8) Сравнить ускорения шарнира рабочего ползуна, полученные методом планов и методом диаграмм. Сравнение проводится аналогично сравнению скоростей.

9) Расчеты и определение численных значений всех скоростей и ускорений для одного положения механизма подробно описать в пояснительной записке (ПЗ), а результаты расчетов для остальных положений механизма свести в соответствующие таблицы.

4.2 Построение плана механизма

Масштабный коэффициент μ_l, (м/мм·ч) показывает, сколько миллиметров действительной длины содержится в одном миллиметре чертежа.

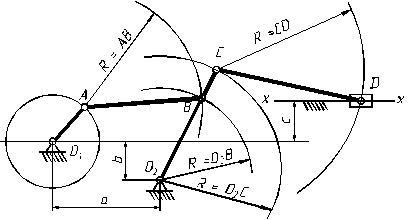
В качестве примера проведем исследование механизма, представленного на рис. 6, у которого ведущее звено 1 (кривошип О₁А) вращается с частотой n₁ против часовой стрелки и заданы размеры звеньев механизма.

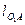
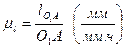
Действительная длина ведущего звена – (мм). На чертеже изобразим ведущее звено отрезком О₁А (мм.ч). Тогда масштабный коэффициент будет равен:

. (2)

Размеры на чертеже для остальных звеньев определяются в соответствии с выбранным масштабом, например:

.

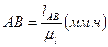
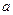
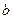
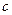
Рассмотрим построение кинематической схемы механизма методом засечек в произвольном положении кривошипа. Нанесём на чертеже положение неподвижных осей шарниров О₁ и O₂ на расстоянии по горизонтали и расстоянии по вертикали, а также положение направляющей ползуна х-х на расстоянии по вертикали от точки О₁ (рис.9).

Рис. 9. Схема построения механизма

Из точки О₁ проведем окружность радиусом, равным длине звена O₁A в выбранном масштабе. В произвольной точке дуги нанесём положение шарнира А. Из точки O₂ проведём дугу радиусом, равным длине звена O₂B в выбранном масштабе. Эта дуга представляет собой геометрическое место точек шарнира В. Из точки А проводим дугу радиусом АВ. На пересечении двух дуг получаем точку В.Соединяем точки В и О₂.Точка C находится на пересечении дуги радиусом O₂С, и продолжения звена O₂B. Таким образом, были построены ведущее звено и первая группа Ассура.

Зная положение точки C, приступаем к построению второй группы Ассура. Т.к. ползун перемещается вдоль прямой х-х, то из точки C проведем дугу радиусом, равным длине звена CD в выбранном масштабе до пересечения с этой прямой. Ставим засечку и получаем точку D.

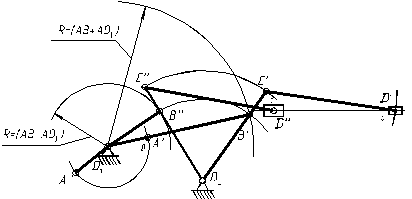
Для проведения кинематического анализа необходимо вычертить кинематическую схему механизма для 12 (24, 36 и т.д.) положений ведущего звена. За начальное (нулевое) принимается такое положение механизма, при котором рабочий инструмент, связанный с ползуном D, находится в начале рабочего хода. Для того, чтобы определить начальное положение механизма, необходимо выяснить, в каких положениях рабочий инструмент совершает полезную работу. Начальное положение будет находиться в крайнем правом или в крайнем левом положении ползуна в зависимости от рабочего хода. Ползун D занимает крайнее положение в том случае, если кривошип О₁А и шатун АВ либо вытянутся в одну линию (на рис. 10 шарнир А в этом положении обозначен А¢), либо накладываются один на другой (А¢¢).

Для определения крайнего правого положения точки D нужно из точки О₁ сделать засечку радиусом (О₁А+АВ) на дуге движения точки В (получаем точку В¢). Производя засечку из точки О₁ радиусом (АВ-О₁А), определим точку В¢¢, соответствующую крайнему левому положению точки D. Все остальные построения производим аналогично описанным выше. Построение крайних положений ползуна (точка D) представлено на рис. 10.

Рис. 10. Схема построения крайних положений механизма

Пусть в нашем случае начало рабочего хода ползуна находится в его крайнем правом положении. Точка А кривошипа описывает окружность относительно оси О₁. Разделим эту окружность, начиная с точки А¢, на 12 равных частей (каждое положение через 30º) (рис.11) и вычертим 12 положений кинематической схемы механизма ([2], стр.92-94). Пронумеруем положения от 0 до 12 по ходу вращения кривошипа (положения 0 и 12 совпадают).

Рис. 11. Схема механизма в 12 положениях

Далее необходимо построить траектории движения центров тяжести звеньев. Принимаем, что центр тяжести стержневых звеньев находится посередине звена (если его положение не задано в задании), а центр тяжести ползуна совпадает с кинематической парой 5-0. Траектория движения центра тяжести звена строится путем последовательного соединения плавной линией точек центров тяжести звена в двенадцати положениях механизма для каждого из подвижных звеньев (см. рис. 11). Обычно центр тяжести кривошипа О₁А находится в точке О₁.

Кинематическое исследование механизма будем вести от ведущего звена для каждой группы Ассура в порядке их присоединения.

Источник

Графическое определение положений звеньев механизма

Независимые между собой параметры, однозначно определяющие положение и движение механической системы, называют обобщенными ко­ординатами. Из курса теоретической механики известно, что количество обобщенных координат равно числу степеней свободы системы, поэтому, установив число степеней свободы механизма, необходимо выбрать столь­ко же обобщенных координат. Как правило, в механизме с одной степенью свободы имеется одно начальное (входное) звено, поэтому за обобщенную координату обычно принимается или угол поворота вращающегося звена, или линейная координата прямолинейно движущегося звена.

Для определения положений звеньев механизма в стандартном масштабе строится его кинематическая схема. Определение положений звеньев покажем для механизма, приведенного на рис. 1.1.

Масштабный коэффициент выбирается таким образом, чтобы длина самого большого звена (1_тах) не превышала на чертеже 150. 180мм. Мас­штабный коэффициент измеряется в м/мм и определяется из формулы

(1-3)

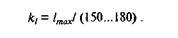
Рис. 1.4. Построение положений звеньев механизма

Для того, чтобы графически определить кинематические величины, описывающие движение звеньев механизма, производятся построения так называемых планов скоростей и ускорений.

1.3. Построение плана скоростей плоского механизма

Основу построения плана скоростей составляет векторная формула определения скорости точки плоской фигуры

(1.4)

(1-5)

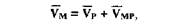
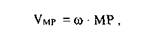
ω- угловая скорость плоской фигуры.

Чтобы воспользоваться векторной формулой, необходимо сначала построить в определенном масштабе (1:1; 1:2; 1:2,5; 1:4; 1:5; 1:10 и т.д.) план механизма в заданном положении. Затем нужно выбрать масштабный коэффициент, который равен отношению скорости полюса к длине отрез­ка, изображающего эту величину. Для обеспечения требуемой точности построения длину отрезка принимают равной 40. 60 мм:

(16)

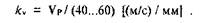
После этого в выбранном масштабе строится векторный треугольник по уравнению (1.4), в котором вектор Vм является замыкающим вектором, а V_mp перпендикулярен к отрезку МР. Такие построения проводятся для всех характерных точек механизма (как правило, кинематических пар) на одном рисунке.

Построение плана скоростей произведем для механизма, изобра­женного на рис. 1.4 во втором положении, для следующих исходных дан­ных:

ОА = 0,1 м; АВ = 0,4 м; ВС = 0,15 м; СО, = 0,15 м; СБ = 0,5 м; ОО, = 0,4 м; угловая скорость кривошипа (звена 1) ω₁ = 10 рад/с.

Решение задачи начинаем с определения модуля скорости точки А начального звена 11

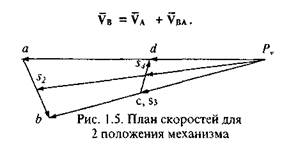
Изобразим вектор скорости V_A из некоторой точки Р_v которая назы­вается полюсом плана скоростей. Этот вектор всегда направлен перпенди­кулярно начальному звену 1 в сторону его движения (рис. 1.5).

Примем длину этого вектора равной 50 мм, тогда масштабный коэф­фициент скорости равен

В конце вектора поставим стрелку и точку а. Скорость точки В определяется в соответствии с векторным уравнением (1.4) в виде:

В силу того, что точка В принадлежит третьему звену, совер­шающему вращательное движение вокруг точки O₁, вектор скорости Vв направлен перпендикулярно третьему звену. Кроме того, вектор V_ba пер­пендикулярен звену 2 и потому точку b на плане скоростей получим как точку пересечения перпендикуляров к направлениям звеньев 2 и 3 в рас-

четном положении, проведенных соответственно через точки а и p_v. Ве­личину скорости точки В найдем, измерив длину отрезка Р, Ь на плане скоростей и умножив ее на масштаб:

Угловая скорость вращения третьего звена находится из формулы

Для определения угловой скорости звена 2 необходимо скорость V_ba во вращательном движении звена ВА вокруг полюса А разделить на длину этого звена:

Точка С принадлежит третьему звену, совершающему вращательное движение вокруг точки O₁ с угловой скоростью ω₃ • Следовательно, вектор скорости Ус направлен перпендикулярно к третьему звену, а его модуль можно найти из формулы

Таким образом, точке С, лежащей на середине звена O₁B механизма, соответствует точка с плана скоростей, лежащая на середине отрезка Р_v b. Заметим, что если одна из скоростей точек (К) какого-либо звена (КL) на плане скоростей уже построена (k), то положение любой другой точки (m) может быть установлено из соотношения пропорциональности:

Завершая построение плана скоростей, определим величину и на­правление скорости точки D. Для этого воспользуемся векторной форму­лой

Проводим из конца вектора Vс прямую, перпендикулярную звену 4, а из полюса P_v — прямую, параллельную направляющим ползуна 5, т.е. ли­нии OD. Точка пересечения этих прямых есть конец вектора V_D, т.е. точка d: Модуль скорости точки d находится путем умножения длины отрезка P_vd на масштабный коэффициент k_v‘.

Угловую скорость вращения четвертого звена находим из формулы

Для динамического анализа механизма необходимо знать скорости центров масс звеньев. Полагая, что центры масс звеньев расположены в середине отрезка, соединяющего кинематические пары, отметим соответ­ствующие точки на плане скоростей. Разделив пополам отрезки аb, Р_v b, cd, получим точки S₂, S₃, S₄. Измерив расстояния P_vS₃, P_vS₄ находим соот­ветствующие скорости:

1.4. Построение плана ускорений плоского механизма

Основой построения плана ускорений служит векторная формула, определяющая ускорение точки плоской фигуры:

(1.7)

(1.8)

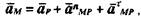
где ω и ε, соответственно, угловая скорость и угловое ускорение плоской фигуры.

Перед началом построений выберем масштабный коэффициент, рав­ный отношению ускорения к длине отрезка, изображающего эту величину. Для обеспечения требуемой точности построения длину отрезка прини­мают равной 80. 100 мм:

(1-9)

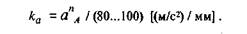
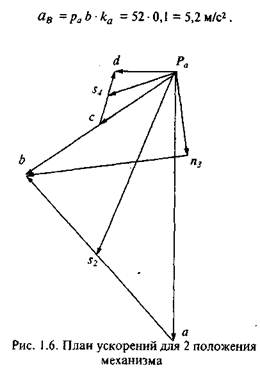
Изобразим вектор ускорения a n _A из некоторой точки р_а, которая на­зывается полюсом плана ускорений. Этот вектор всегда направлен парал­лельно начальному звену 1 (рис. 1.6).

Примем длину этого вектора равной 100 мм, тогда масштабный ко­эффициент ускорения равен

В конце вектора поставим стрелку и точку а. Ускорение точки В находим в соответствии с векторной формулой (1.7):

а вектор a n _BA направлен вдоль звена АВ от точки В к точке А. Длина, вектора, изображающего это ускорение, равна величине этого ускорения, деленной на масштабный коэффициент: a n _BA /к_а = 0,08 / 0,1 = 0,8 мм. В пределах погрешности построений (с точностью до 1 мм) изобразить этот отрезок на чертеже не представляется возможным, поэтому полагаем, что он равен нулю. Таким образом, точка b плана ускорений лежит на перпен­дикуляре к АВ, проведенному из точки а.

С другой стороны, точка В принадлежит звену 3, совершающему вращательное движение вокруг точки О₁ Следовательно, полное ускоре­ние точки В равно сумме ее нормальной и касательной составляющих :

причем по величине

а направлен этот вектор вдоль ВО₁ от В к O₁. Длина вектора, изображаю­щего это ускорение, равна величине этого ускорения, деленной на мас­штабный коэффициент: a n _B/ к_а = 2,84 / 0,1 = 28,4 мм. Из полюса плана ускорений проводим отрезок р_ап₃ длиной 28 мм параллельно звену ВО₁. Этот вектор изображает нормальное ускорение точки В. Из конца этого вектора проводим перпендикулярно ему линию, по которой направлена касательная составляющая ускорения точки В, до пересечения с перпенди­куляром к АВ, проведенным из точки а. Полученную точку обозначаем че­рез b. Замерив длину отрезка р_а b, находим полное ускорение точки В :

Замеряем на чертеже длину вектора п₃b (в данном примере она равна 43 мм), изображающего касательную составляющую ускорения точки В. Его величина позволяет определить угловое ускорение звена 3:

Угловое ускорение звена 2 находим аналогично:

Далее находим ускорение точки D как векторную сумму:

где

Длина вектора, изображающего это ускорение, равна a n _DC/ к_а = 0,01 • 0,1 = = 0,1 мм. Изобразить этот отрезок на чертеже не представляется возмож­ным, поэтому полагаем, что он равен нулю.

Далее находим угловое ускорение четвертого звена;

Определим ускорение центров масс звеньев 2 и 4. Для определе­ния ускорения центра масс второго звена разделим на плане ускорений отрезок аb пополам точкой S2 и соединим ее с полюсом плана ускорений:

Аналогично находим положение точки S4 и ускорение центра масс звена 4:

1.5. Особенности построения планов скоростей и ускорений кулисного механизма

Вкулисных механизмах одно из звеньев, называемое кулисой, может перемещаться поступательно относительно другого подвижного звена (на рис. 1.7,а звено 3 является кулисой). В результате кулиса совершает слож­ное движение, методы кинематического анализа которого несколько отли­чаются от изложенных выше.

Напомним, что сложное движение твердого тела раскладывается на два составляющих движения: относительное (относительно подвижной

системы отсчета) и переносное (движение подвижной системы отсчета от­носительно неподвижной). Скорость точки в сложном движении опреде­ляется как векторная сумма;

(1.10)

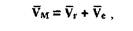
При определении ускорения точки в сложном движении следует иметь в виду, что наряду с относительным и переносным ускорением нуж­но учитывать еще и ускорение Кориолиса:

(1.11) причем для плоского переносного движения

(1.12)

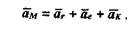
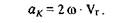
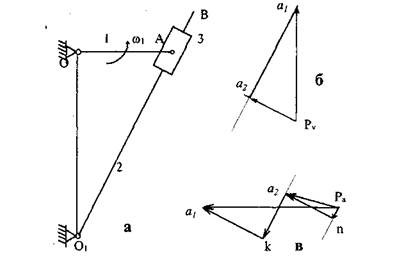
Рассмотрим построение плана скоростей для кулисного механизма, изображенного на рис. 1.7,а при следующих исходных данных : ОА = 0,2 м; O₁O = 0,34 м; угловая скорость кривошипа ω₁= 10 рад/с. Проведем графи­ческие построения для расчетного положения, в котором ОА перпендику­лярно О₁O

Начальное звено ОА совершает вращательное движение, и потому скорость точки А звена 1 может быть найдена как

Вектор скорости V_A1 направлен перпендикулярно звену 1 в сторону его движения.

Выбрав произвольную точку ру за полюс плана скоростей, изобразим вектор скорости V_A1 задавшись его длиной на плане скоростей в 50 мм. Тогда масштабный коэффициент найдем как

После построений получим на плане скоростей точку a₁. В силу того, что точка А кулисы 3 совершает сложное движение, абсолютная скорость V_a1 может быть представлена в виде суммы (1.10), в которой вектор пере­носной скорости точки А звена 2 V_a2 направлен перпендикулярно к ОА (т.к. переносное движение вращательное), а вектор относительной скорос­ти V_r— вдоль прямой O₁A (т.к. относительное движение прямолинейное):

а отрезок a₁а₂ относительную скорость;

При заданном направлении движения вектор относительной скорос­ти направлен от а₂ к а₁.

Величина угловой скорости звена 2 может быть найдена как отно­шение

Переходим далее к построению плана ускорений. Выбрав полюс плана ускорений p_a, зададимся длиной вектора ускорения точки А в 50 мм. При этом

Тогда масштабный коэффициент равен

Изображаем в выбранном масштабе вектор а_A1 на плане ускорений, направляя его вдоль звена 1 отточки А к оси вращения О.

Абсолютное ускорение а_A1 может быть представлено в виде вектор­ной суммы (1.11):

в которой ускорение точки А звена 2 имеет две составляющие г

ускорение Кориолиса

и направлено перпендикулярно к звену 2 в сторону его переносного вращения.

Из полюса плана ускорений изображаем вектор переносного нор­мального ускорения параллельно АО₁ от А к O₁ величиной

Касательная составляющая ускорения точки А звена 2 направлена перпендикулярно к О₁А, а значит перпендикулярно и к р_ап. Следователь­но, точка аг расположена на перпендикуляре к нормальному ускорению.

Вектор ускорения Кориолиса длиной

1.6. Аналитическое определение скоростей и ускорений звеньев меха­низма

Графические методы кинематического анализа, являясь довольно простыми и наглядными, не обладают точностью, которая бывает необхо­дима при расчетах механизмов. В последнее время получили распростра­нение аналитические методы, с помощью которых исследование кинема­тики механизмов может быть осуществлено с любой степенью точности.

Кроме того, аналитические методы легко поддаются алгоритмизации, что немаловажно при решении задач кинематики механизмов на персональных ЭВМ.

Аналитический метод,или метод замкнутого контра, состоит в ре­шении векторных уравнений, описывающих движение некоторой совокуп­ности звеньев механизма, для которой каждое из этих уравнений содержит не более двух неизвестных геометрических величин. Для механизмов с од­ной степенью свободы такой совокупностью может служить механизм, движение которого задано полностью, с присоединенной к нему группой Ассура.

Рис. 1.8. Кривошипно-ползунный механизм

В соответствии со своим названием метод замкнутого контура пред­полагает построение векторного многоугольника, начало первого вектора у которого совпадает с концом последнего. Для плоских механизмов таким многоугольником служит система векторов, направленных последователь­но от одной кинематической пары к другой.

Так, для кривошипно-ползунного механизма, изображенного на рис. 1.8, замкнутым контуром может служить система векторов

а в проекции на ось Оу:

Таким образом, имеем два алгебраических уравнения с двумя неиз­вестными величинами, решая которые найдем:

В силу известных ограничений, накладываемых на величину угла, задаваемого функцией агсsin, можно заметить и ограничения на выбор не­известного углового параметра:

Следовательно, выбирая в качестве неизвестного параметра угол по­ворота одного из звеньев механизма, если этот выбор не оговорен заранее, следует следить за тем, чтобы этот угол лежал в заданных пределах.

При необходимости вычисления скоростей и ускорений точек звеньев механизма, координаты которых не вошли в число геометрических пара­метров, определяющих положение механизма, следует воспользоваться векторными формулами плоскопараллельного движения вида (1.4) и (1.7).

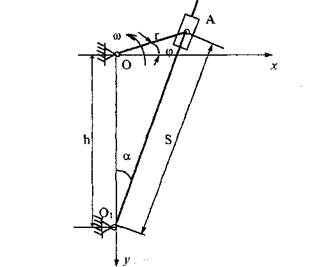
В качестве примера определим скорость и ускорение точки С звена О₁В кулисного механизма, изображенного на рис. 1.7,а при следую­щих исходных данных: ω_OA = ω = сonst, ОА = г, О₁O = h= г√3 О₁С = г. В расчетном положении ОА±О₁O.

За геометрические параметры, описывающие положение механизма в текущем положении (при произвольном расположении кривошипа, зада­ваемом углом φ, примем: угол поворота а звена O₁В и расстояние S от оси вращения этого звена до шарнира А. Из векторного уравнения

в проекциях на оси координат хиу (рис. 1.9) имеем:

Продифференцируем по времени уравнения проекций

Рис. 1.9. Текущее положение кулисного механизма

При φ= 0, φ= ω, ά = 30°, S = 2 г получим систему уравнений

Для определения ускорений второй раз продифференцируем уравне­ния проекций:

откуда при φ = 0, φ = ω, φ = 0 и найденных выше значениях имеем:

Выбирая неподвижную точку О₁ звена O₁В за полюс, найдем ускоре­ние точки С:

Силы трения относятся к силам вредных сопротивлений. Они вызывают нагрев и износ трущихся деталей, а также дополнительный расход энергии.

Различают несколько видов трения: трение сухое, трение полусу­хое и трение жидкостное. По видам относительного движения разли­чают: трение качения, трение скольжения, кинетическое трение, трение при ударе, трение покоя ^статическое трение,).

Принято считать в первом приближении, что для сил сухого трения скольжения выполняются законы Кулона-Амонтона:

— сила трения скольжения пропорциональна нормальному давле­нию;

— сила трения зависит от вида материалов и состояния трущихся поверхностей;

— для большинства пар трения сила трения не зависит от относительной скорости скольжения;

— сила трения не зависит от величины площади трущихся поверхностей;

— сила трения покоя больше силы трения при движении;

— сила трения всегда направлена в сторону, противоположную относительной скорости скольжения;

— сила трения возрастает с увеличением времени контакта. Закон Кулона-Амонтона имеет вид

(2.3)

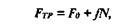
Трение оказывает существенное влияние на работоспособность поступательной кинематической пары.

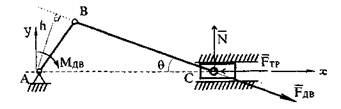
Рис. 2.5. Схема сил в кривошипно-ползунном механизме

Рассмотрим условия равновесия кривошипно-ползунного механиз­ма, изображенного на рис. 2.5. Составим уравнения проекций на гори­зонтальную ось х и вертикальную ось у:

Поскольку при равновесии F_ТР≤ f*N, если пренебречь размерами ползуна, то легко заметить, что

Таким образом, независимо от величины Мдв ползун двигаться не будет (т.е. механизм неработоспособен), если

Такое явление хорошо известно из курса теоретической механики, где объясняется, что силы, действующие на материальный объект, находя­щийся на. шероховатой поверхности, должны быть приложены вне угла трения, чтобы сдвинуть этот объект с места. Таким образом, условие ра­ботоспособности механизма (возможности движения ползуна по на­правляющим) имеет вид:

(2.4)

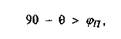
Иной характер носят силовые зависимости при жидкостном трении, основы теории которого разработал Р.Р.Петров в конце 19 в. При относительном движении тел, разделенных жидкостью, наблюдается сдвиг отдельных слоев жидкости друг относительно друга. Таким об­разом, жидкостное трение сводится к вязкому сдвигу, а сила трения определяется в соответствии с формулой

(2.5)

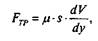
Возникновение жидкостного трения во вращающейся или посту­пательной паре возможно при следующих условиях:

1) смазочная жидкость (смазка) должна удерживаться в зазоре, это обеспечивается превышением силы сцепления между телом и смазкой над силами сцепления между слоями смазки;

2) смазка должна полностью разделять поверхности, что обеспе­чивается соответствующей обработкой трущихся поверхностей;

3) в слое смазки должно быть такое давление, которое уравно­вешивает внешнюю нагрузку, что обеспечивается нагнетанием смазки и клиновидной формой зазора.

(2.6)

(2.7)

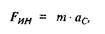
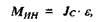
В частности, если обратимся к примеру расчета пятизвенного механизма (рис. 1.4), то для звена 2 при т₂ = 10 кг и j_s2 = 1 кг • м 2 полу­чим;

Источник