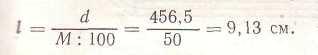Как построить и оцифровать линейный масштаб
Как построить линейный масштаб, если известны его основание и численный масштаб?



Линейный масштаб строят и используют для удобства пользования картами и планами, он позволяет избежать расчетов при переводе длин линий местности в масштаб карты или плана и наоборот.
На топографических картах и планах линейный масштаб вычерчивается под южной рамкой карты или плана.
Для построения линейного масштаба, на прямой несколько раз откладывается отрезок одинаковой длины, который называется основанием масштаба. Чаще всего основание линейного масштаба принимается равным 2 см.
Далее линейный масштаб подписывается в соответствии с численным масштабом карты или плана.
Например, отрезок длиной 2 см, на топографическом плане масштаба 1:5000, будет равен линии длиной 100 м на местности (2 см * 5000 = 10000 см = 100 м).
Для повышения точности построения или измерения отрезков на картах или планах, крайний левый отрезок линейного масштаба делят на 10 или 20 равных частей, которые называются делениями основного масштаба.
Решение задач по топографическим планам
Масштабы: численный, линейный и поперечный
Масштабом
горизонтальным проложением линии
Применяется три типа масштаба:
численный, линейный и поперечный.
Численным масштабом
Численный масштаб – величина неименованная. Он записывается так: 1:1000, 1:2000, 1: 5000 и т.д., причём в такой записи 1000, 2000 и 5000 называется знаменателем масштаба М.
Численный масштаб говорит о том, что в одной единице длины линии на плане (карте ) содержится точно столько же единиц длины на местности. Так, например, в одной единице длины линии на плане 1:5000 содержится точно 5000 таких же единиц длины на местности, а именно: один сантиметр длины линии на плане 1:5000 соответствует 5000 сантиметрам на местности (т.е. 50 метрам на местности); в одном миллиметре длины линии на плане 1:5000 содержится 5000 миллиметров на местности (т.е. в одном миллиметре длины линии на плане 1:5000 содержится 500 сантиметров или 5 метров на местности) и т.д.
При работе с планом в ряде случаев пользуются линейным масштабом.
Линейный масштаб

Рис.1
Основанием линейного масштаба называется отрезок АВ линейного масштаба (основная доля масштаба), равный обычно 2 см. Он переводится в соответствующую длину на местности и подписывается. Крайнее левое основание масштаба делят на 10 равных частей.
Наименьшее деление основания линейного масштаба равно 1/10 основания масштаба.
Пример: для линейного масштаба (использующегося при работе на топографическом плане масштаба 1:2000), показанного на рисунке 1, основание масштаба АВ равно 2 см (т.е. 40 метрам на местности), а наименьшее деление основания равно 2 мм, что в масштабе 1:2000 соответствует 4 м на местности.
Отрезок cd (рис. 1), взятый с топографического плана масштаба 1:2000, состоит из двух оснований масштаба и двух наименьших делений основания, что, в итоге, соответствует на местности 2х40м+2х2м = 88 м.
Поперечный масштаб
Основание AB нормального поперечного масштаба равно, как и в линейном масштабе, также 2 см. Наименьшее деление основания равно CD =1/10 АВ= 2мм. Наименьшее деление поперечного масштаба равно cd = 1/10 CD =1/100 АВ = 0,2мм (что следует из подобия треугольника BCD и треугольника Bcd).
Таким образом, для численного масштаба 1:2000 основание поперечного масштаба будет соответствовать 40 м, наименьшее деление основания (1/10 основания) равно 4 м, а наименьшее деление масштаба 1/100 АВ равно 0,4 м.
Остановимся на одной из важнейших характеристик понятия «масштаб».
Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба. Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1мм. На местности эта величина будет уже равна 0.1 мм х М, где М – знаменатель масштаба.

Рис.2
Поперечный масштаб, в частности, позволяет измерить длину линии на плане (карте) масштаба 1:2000 именно с точностью данного масштаба.
Пример: в 1 мм плана 1:2000 содержится 2000 мм местности, а в 0,1мм, соответственно, 0,1 x М (мм) = 0.1 х 2000 мм = 200 мм = 20 см, т.е. 0,2 м.
Поэтому при измерении (построении) на плане длины линии ее значение следует округлить с точностью масштаба. Пример: при измерении (построении) линии длиной 58,37 м (рис. 3), ее значение в масштабе 1:2000 (с точностью масштаба 0,2 м) округляется до 58,4 м, а в масштабе 1:500 (точность масштаба 0,05 м) – длина линии округляется уже до 58,35 м.

Рис.3
Чтение
топографических планов
Для пользования топографическими планами необходимо изучить условные знаки, принятые для данного масштаба. Условные знаки – графические обозначения, которые показывают местоположение предметов и явлений, а также их количественные и качественные характеристики. Они издаются в виде отдельных таблиц или таблиц на учебных планах. Условные знаки делятся на масштабные (контурные), и внемасштабные.
Масштабными называются условные знаки, которыми местные предметы изображаются в масштабе данного плана, т.е. крупные объекты, например, пашни, луга, леса, моря, озера и т.п.
Внемасштабные условные знаки – знаки, показывающие предметы, которые вследствие своей малости не могут быть изображены в масштабе плана (ширина дорог, колодцы, родники, мосты, опоры ЛЭП, столбы электросети и т.д.). Величина этих знаков не соответствует истинным размерам изображаемых предметов.
Скачать условные знаки для топографических планов:
Задачи, решаемые
по топографическим планам
По топографическому плану можно решить ряд задач, в том числе определить: прямоугольные координаты точки; длину линии; дирекционный угол и румб линии; отметку точки; уклон, крутизну ската и др. Порядок решения этих задач показан на примере учебного плана масштаба 1:2000.
Определение прямоугольных
координат точек
Пример : запись 79,2 означает, что абсцисса линии сетки Х = 79,2 км, т.е. отстоит по оси Х от начала координат на 79200 м. Запись 66,2 означает, что ордината линии сетки Y = 66,2 км, т.е. отстоит по оси У от начала координат на 66200 м.
Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.
Сначала записывают в метрах абсциссу Х (южной) линии квадрата, в котором находится точка А, т.е. Х(южной линии сетки) =79200,0 м. Циркулем и поперечным масштабом определяют расстояние Δх = Y(а)-Y(А) также в метрах с точностью масштаба. Полученную величину Δх=64,8 м прибавляют к абсциссе нижней (южной) линии квадрата Х(южной линии сетки) =79200,0 м и находят абсциссу точки А: Х(А) = 79200,0 + 64,8 = 79264,8 м.

Рис.4
Аналогично определяют ординату точки А: к значению ординаты западной линии сетки квадрата У(западной линии сетки) =66200,0 м прибавляют длину отрезка Δy =y(A)-y(b), равную 141,6 м, и получают Y(А) = 66200,0 + 141,6 = 66341,6 м.
Измерение длин линий
Расстояние между точками А и В измеряется циркулем, значение длины линии АВ находится по поперечному масштабу и записывается с точностью масштаба.
Определение
дирекционного угла
Дирекционным углом α называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана, по ходу часовой стрелки, до направления данной линии.
Дирекционный угол α линии АВ можно измерить с помощью транспортира. На рис. 5 представлены дирекционные углы α1, α2, α3, и α4 четырех линий М-1, М-2, М-3, М-4.

Рис.5

Рис.6
Связь между прямым и обратным дирекционными углами выглядит так:

Рис.7
Например, если прямой румб равен r пр = СВ: 350º, то обратный румб равен r обр= ЮЗ: 350º.

Рис.8
Таблица перехода от дирекционных углов α к румбам r приведена ниже.
Формулы перехода от дирекционных углов к румбам
Определение отметок точек
и крутизны ската линии местности
Высотой Н точки местности называется расстояние по направлению отвесной линии от точки до уровенной поверхности.
Отметкой точки местности называется численное значение высоты точки. Например, Н(А) = 150 м, Н(В) =149 м.
На топографическом плане рельеф изображается надписями отметок отдельных характерных точек, условными знаками (промоина, обрыв и т. п.) и горизонта-лями.
Горизонталями называются замкнутые кривые линии, со-единяющие точки местности с одинаковыми отметками. Горизонтали образуются путём пересечения поверхности местности секущими горизонтальными плоскостями, проведенными через заданное расстояние, которое называется высотой сечения рельефа h.
Заложением называется расстояние d на плане между двумя соседними горизонталями (рис. 9 – 11).

Рис.9
По отметкам двух смежных (соседних) горизонталей можно определить отметку точки, лежащей между ними. Например: отметка первой точки В на нижней (рис. 10) горизонтали H1 = 161 м, отметка второй точки А на верхней (рис. 10) горизонтали H2 = 162 м (т.е. высота сечения рельефа h = 1 м), заложение d = 16,8 м, расстояние от первой горизонтали до точки С равно с = 7,6 м (рис. 10). Тогда (с требуемой точностью до 0,1 м) вычисляем отметку НС точки С по формуле

Рис.11
Чем больше угол наклона, тем скат круче.
Для нашего примера уклон линии местности между горизонталями равен
Масштаб и способы его вычисления с помощью калькулятора онлайн
Отравляясь в лес или поход, мы всегда берем с собой карту. Именно с ее помощью туристы определяют свое местоположение на местности и прокладывают маршрут. Естественно, расстояния на картах показаны не в реальных показателях, а в определенном масштабе.
Соответственно, чтобы научиться читать карту, нужно знать, как определить масштаб в каждом конкретном случае. Именно этому вопросу и будет посвящена сегодняшняя статья.
Карта. План. Профиль.
Конечным результатом топографо-геодезических работ являются чертежи земной поверхности, числовые данные для составления цифровых моделей местности и др. материал, представленный в упорядоченном виде. Чертежи могут быть составлены на бумажной основе, представлены в электронной форме или в виде компьютерной базы данных. Традиционными формами чертежей являются: карта, план, профиль.
При изображении на бумаге, т.е. на плоскости всей земной поверхности или значительных её участков невозможно избежать искажений изображения вследствие кривизны изображаемой поверхности, поскольку при любом способе проектирования на плоскость возникают искажения в длинах линий и углах между ними.
Уменьшенное искаженное за счёт влияния кривизны Земли, плоское изображение всей земной поверхности или значительной её части, построенное по определённым математическим законам, называется картой.
В зависимости от назначения карты при её создании выбирается определённая картографическая проекция, т.е. математический закон проектирования местности на плоскость.
Ортогональную проекцию небольших участков местности (до 20×20 км) на уровенную поверхность можно считать плоской, пренебрегая кривизной Земли. Уменьшенное изображение такой проекции на бумаге будет без искажений, вызванных кривизной Земли, и подобным участку местности.
Таким образом, уменьшенное, подобное изображение на плоскости горизонтального проложения сравнительно небольшого участка земной поверхности называется планом.
Наглядным изображением неровностей земной поверхности является профиль, т.е.уменьшенное изображение её вертикального разреза по выбранной линии.
На планах и картах могут изображаться ситуация и рельеф, либо только ситуация (от франц. Situation — местоположение).
Совокупность изображений на плане местных предметов естественного и искуственного происхождения (река, лес, кустарник, земельный участок, здание, улица и др.), называетсяситуацией местности.
Совокупность неровностей земной поверхности естественного происхождения называется рельефом местности.
Принято считать, что план можно составлять на террито рию, не превышающую площади круга радиусом 10 км.
Если на плане изображены только границы объектов ме стности, его называют контурным (рис. 3.1, а). Если, кроме контуров, на план нанесен и рельеф, такой план называюттопографическим (рис. 3.1,б).
Рис.3.1. Контурный (а) и топографический (б) планы.
Картой называют чертёж, на котором может быть изображена поверхность всей Земли или любой её части в обобщенном и уменьшенном виде.
Карты могут иметь различное назначение: сельскохозяйственные, кадастровые, экономические, политические и т.д. — это так называемые тематические или специальные карты, на них показывают контуры ситуации и специальную нагрузку. Карты на которых, кроме контуров ситуации, изображен рельеф земной поверхности, называют общегеографическими. Общегеографическая основа карты является каркасом для построения тематических карт.
При любых измерениях по планам и картам следует помнить, что масштаб плана во всех его точках одинаковый, а масштаб во всех точках карты, как правило, различен.
| к предыдущему разделу | к следующему разделу |
Инструкция для измерений и вычислений
Тщательно исследуйте план и определите здание, которым будете заниматься.
К примеру, стена хозяйственной постройки реальной протяженностью 4 метра занимает на плане 2 см. Переводим эту величину в сантиметры и получаем, что 2 см на рисунке отвечает 400 см в реальности. При этом используем простое деление:
Значит, 1 см изображенный на карте — это 2 м на территории.
В кинотехнике
В кинотехнике тоже важна точность масштаба времени. Под последним подразумевается количественный показатель замедления либо ускорения движения, который будет равняться отношению проекционный частоты кадров к частоте съемочной.
Рассмотрим это на простом примере. Проекционная частота кадров при съемке фильма составляет 24 кадра/сек. Киносъемка производилась при этом «со скоростью» 72 кадра/сек. Масштаб времени в данном случае будет равен 1:3.
А что тогда будет означать, к примеру, 2:1? Это ускоренное в два раза по сравнению со стандартным протеканием происходящего на экране.
Масштаб и классификация карт по нему
Чем больший участок Земли нужно изобразить, тем в большее количество раз нужно уменьшить расстояния на карте по сравнению с действительным. На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
Подробно можно показать небольшую площадь, посёлок, район, город. Тут будет видны уже и форма и размер зданий, расположение лесопарков, небольшие реки и др. Это возможно потому, что расстояния уменьшены несильно, масштаб карты достаточно крупный.
По масштабу карты делят на:
Нужно запомнить правило: чем больше величина масштаба, тем мельче масштаб карты, чем крупнее масштаб, тем подробнее карта.


В программировании
В этой сфере будет важен так называемый масштаб времени. Разберемся, что это.
В ОС с разделением времени весьма важную роль имеет предоставление конкретно взятым задачам «режима реального времени». Он отличается тем, что обработка внешних событий идет без дополнительных задержек или пропусков. Здесь важным будет еще одно понятие — «реальный масштаб времени». Но стоит понимать, что к масштабу на картах он прямого отношения не имеет. Это всего лишь терминологическая условность.
Что это?
Масштаб — это важное уточнение, показывающее, во сколько каждая линия, что была нанесена на чертеж, план, меньше или больше настоящих размеров объекта, который она изображает. Такие уточнения представляются на чертежных документах и картах как численно, так и графически.
Масштабы планов, точность масштабов — понятия, которые можно встретить в самых разнообразных сферах:
Некоторые из этих применений, их особенности мы рассмотрим по ходу статьи.
Особенности расчетов
Итак, вам нужно представить какой-то рисунок, план или деталь. Как сделать это с наименьшими затратами времени и наиболее точно? Для этого необходимо: проект дома, изображение построек на карте или плане, чертеж деталей, калькулятор, принадлежности для черчения.
Удобнее всего чертить объекты, объемные детали или предметы, используя отношение 1:1. Это означает, что метр реальной местности пропорционален сантиметру на рисунке. Но чаще всего возникает необходимость применить масштабы другого порядка, такие как 1:2,1:10 и так далее. Это происходит в том случае, если территория большая, а изобразить ее надо компактно. Если объект совсем крошечный, но при производстве важны даже самые мелкие детали, его изображают используя масштаб 10:1 или даже больше.
Пошаговая инструкция, как определить масштаб
Обычно составитель указывает линейный или численный масштаб чертежа или карты, с помощью которого и определяется расстояние между объектами на местности. Но иногда топографическая карта не содержит этой информации, и определять масштаб приходится самостоятельно. В этом пригодятся некоторые знания в географии (рисунок 1).
На самом деле вычисление масштаба – простая задача, если знать, как правильно действовать. Из инструментов вам понадобится сама карта и линейка.
Самый простой способ определить масштаб – использовать километровую сетку. Она проставлена на любой карте, а стороны каждого квадрата соответствуют определенному количеству километров.

Рисунок 1. Умение определить масштаб — полезный навык для туриста
Узнать это расстояние можно по подписям у выхода линий сетки к краям карты. Например, на подписи указано, что расстояние между двумя линиями сетки составляет 1 км. Теперь измерьте это расстояние линейкой. Предположим, вы получили показатель в 2 см. Соответственно, каждый сантиметр карты соответствует 500 метрам на местности, а сам масштаб чертежа составляет 1:50000.
В моделизме
Для каждого из видов стендового (или масштабного) моделизма определены свои масштабные ряды. Они состоят из нескольких масштабов, характеризующихся определенной степенью уменьшения. Что интересно, для каждого из видов моделизма (железнодорожного, автомобильного, судомоделизма, военной техники, авиамоделизма) есть определенные исторически сформированные масштабные ряды, которые не пересекаются с иными.
Здесь масштаб исчисляется по простой формуле:
Измерение расстояний на карте шагом циркуля.
Ломаные линии удобно измерять путем последовательного наращивания раствора циркуля прямолинейными отрезками. Измерение расстояний и длин кривых линий производится последовательным отложением шага циркуля. Величина шага циркуля зависит от степени извилистости линии, но, как правило, не должна превышать 1 см. Для исключения систематической ошибки длину шага циркуля, определенную по масштабу или линейке, следует проверять измерением линии километровой сетки длиной 6–8 см.
Длина извилистой линии, измеренной по карте, всегда несколько меньше ее действительной длины, так как измеряются не кривая линия, а хорды отдельных участков этой кривой. Поэтому в результаты измерений покарте приходится вводить поправку – коэффициенты увеличения расстояний.
Лабораторная работа Построение линейного масштаба.
Задание
Задание 1. Работа с численными масштабами:
А). Вычислить длины линий на плане в сантиметрах, по их длинам на местности в метрах.
Б). При помощи калькулятора вычислить длины линий на местности в метрах.
Задание 2. Построение графических масштабов:
Построить линейный масштаб с основанием l = 2 см(5см), т = 10.
Задание 3. По данным задания 1, пользуясь построенными графическими масштабами и измерителем, отложить на бумаге длины линий на линейном масштабе.
Просмотр содержимого документа
«Лабораторная работа Построение линейного масштаба.»
Лабораторная работа №1
Тема: Построение линейного масштаба.
Цель: научить студентов строить линейный масштаб.
Методическое обеспечение: масштабные линейки, циркуль-измеритель, чертежные принадлежности и лист формата А4, учебные геодезические карты масштабов 1:50000; 1:25000; 1:10000.
Задание 1. Работа с численными масштабами:
А). Вычислить длины линий на плане в сантиметрах, по их длинам на местности в метрах.
Б). При помощи калькулятора вычислить длины линий на местности в метрах.
Задание 2. Построение графических масштабов:
Построить линейный масштаб с основанием l = 2 см(5см), т = 10.
Задание 3. По данным задания 1, пользуясь построенными графическими масштабами и измерителем, отложить на бумаге длины линий на линейном масштабе.
1.1. Численный масштаб 1:100. Сколько метров в 1 см?
1.2. Численный масштаб 1:2000. Сколько метров в 10 см?
1.3. Численный масштаб 1:5000. Сколько метров в 1 мм?
2.Последовательность выполнения практической работы:
Работа с численными масштабами
2.1. Вычислить длины линий на плане в сантиметрах, по их длинам на местности в метрах. Исходные данные см. таблицу №1.
Длина линии на местности, м
Масштабы планов 1: М
Чтобы получить длину линии на плане в сантиметрах, надо ее длину на местности в метрах разделить на знаменатель численного масштаба плана М, уменьшенный в 100 раз.
Длина линии на местности d = 456,5 м, масштаб плана 1:5000. Длина этой линии на плане равна:
2.2. При помощи калькулятора вычислить длины линий на местности в метрах. Исходные данные см. таблицу №2.
Длина линий на плане, см
Масштабы планов 1: М
Чтобы получить длину линии на местности в метрах, нужно ее длину на плане в сантиметрах умножить на знаменатель масштаба плана и результат разделить на 100 (отделить запятой два знака справа налево).
l = 17,28 см, масштаб 1:2000. Длина этой линии на местности равна:
d = (l*М) : 100 = 17,28 * 2000 : 100 =345,60 м.
Построение графических масштабов:
2.3. Построить линейный масштаб с основанием l = 2 см (четные варианты) и l =5см (нечетные варианты), т = 10.
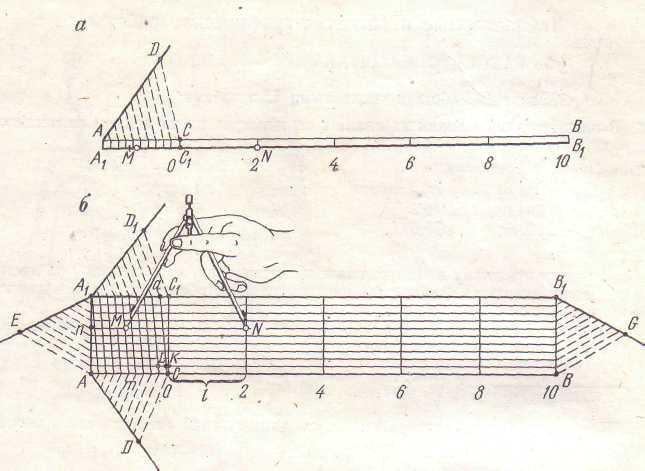
На листе чертежной бумаги (рис. 1, а) прочерчены две параллельные прямые (для наглядности), на которых измерителем отложено 6 отрезков, равных по длине заданному основанию l = 2 см. Эти отрезки называют большими делениями масштаба. Левое основание (большое деление) АС разделено на 10 малых делений длиной по 2 мм.
Для большей точности разделения использован способ проведения параллельных линий при помощи треугольника и линейки. Под произвольным углом к линии АС проводят линию АD, на ней последовательно от точки А откладывают 10 равных отрезков длиною несколько более 2 мм, отмечая полученные точки уколом. Треугольник одним катетом прикладывают к линии DС, к другому его катету прикладывают линейку. Треугольник перемещают вдоль линейки и, проводя линии через отмеченные течки на отрезке АD, получают соответствующие точки на АС. Масштаб вычерчен тушью.
Рис. 1. Построение графических масштабов:
П р и м е р. На плане масштаба I : 2000 отложить линию длиной 52,4 м.
2.4. По линейному масштабу (см. рис. 1, а) расстояние между иголками измерителя MN равно одному большому и 5,6 малого деления, при этом 0,6 малого деления взято на глаз.
3.1. Дать понятие численного масштаба.
3.2. Дать понятие линейного масштаба.
3.3. Что называется точностью масштаба.
4.Защита работы: отчет и контрольные вопросы.
Поклад Г.Г. Геодезия / Г.Г.Поклад. – М.: Недра,1988. – с. 33.