Как построить график звуковой волны
Как построить график звуковой волны
Перед тем, как приступить к рассмотрению темы, дадим определение такому явлению, как звук.
Звук или звуковые волны – это волны, которые способно воспринять человеческое ухо.
Волнам звукового диапазона свойственно распространяться как в газе, так и в жидкости (продольные волны), и в твердом теле (продольные и поперечные волны). Особенно интересно для науки заниматься изучением распространения звуковых волн в газообразной среде, что по сути есть среда нашего обитания.
Акустика – это направление физики, занимающееся изучением звуковых явлений.
Звуковые волны в газе зачастую называют волнами плотности или волнами давления.
Одной из ключевых характеристик звука является скорость распространения.
Скорость распространения – величина, описывающая звуковую волну, задаваемая инертными и упругими свойствами среды и определяемая для продольных волн в любой однородной среде при помощи формулы:
В указанной формуле B является модулем всестороннего сжатия, ρ – средней плотностью среды.
Формула Лапласа
Формула Лапласа для определения скорости звука имеет запись:
Где p является значением среднего давления в газе, ρ – средней плотности, а γ есть некоторая константа, находящаяся в зависимости от свойств газа.
Формула Лапласа может быть записана несколько иначе, если использовать уравнение состояния идеального газа. Таким образом, окончательный вид формулы для определения скорости звука будет такой:
Для наглядности приведем некоторые примеры.
Когда звук распространяется в гелии ( M = 4 · 10 – 3 к г / м о л ь ) : υ = 970 м / с ;
Характеристики звуковых волн
Помимо скорости распространения звук имеет и другие характеристики, связанные с восприятием его человеческими органами слуха.
Громкость звука
Рассуждая о том, как человеческое ухо воспринимает звук, в первую очередь мы говорим об уровне громкости, который зависит от потока энергии или интенсивности звуковой волны. А то, как воздействует звуковая волна на барабанную перепонку, зависит от звукового давления.
Звуковое давление – это амплитуда p 0 колебаний давления в волне
Природа отлично потрудилась, создавая такое совершенное устройство, как человеческое ухо: оно способно воспринимать звуки в обширнейшем диапазоне интенсивностей. Мы имеем возможность слышать как слабый писк комара, так и грохот вулкана.
Порог слышимости – минимальное значение величины звукового давления, при котором звук этой частоты еще воспринимается человеческим ухом.
Болевой порог – это верхняя граница диапазона слышимости человека; та величина звукового давления, при котором звук вызывает в человеческом ухе ощущение боли.
Человеческое ухо, восприимчивое к звукам такого огромного диапазона интенсивности, допустимо сравнить с прибором, которым возможно измерить как диаметр атома, так и размеры футбольного поля.
Для общей информированности заметим, что обычным разговорам людей в комнате соответствует интенсивность звука, примерно в 10 6 раз превышающая порог слышимости, а интенсивность звука на рок-концерте находится очень близко к болевому порогу.
Высота звука
Высота звуковой волны – еще одна характеристика звука, влияющая на слуховое восприятие. Человеческие ухо воспринимает колебания в гармонической звуковой волне как музыкальный тон.
Высокий тон – это звуки с колебаниями высокой частоты.
Низкий тон – это звуки с колебаниями низкой частоты.
Звуки, которые издают музыкальные инструменты, а также звуки голоса человека значимо отличаются друг от друга по высоте тона и по диапазону частот.
Октава – это диапазон колебаний звука, который соответствует изменению частоты колебаний в 2 раза.
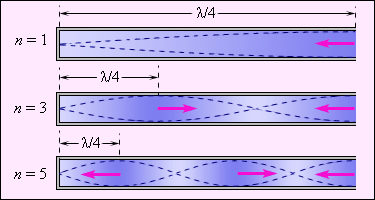
Говоря о частоте звука, который извлекается при помощи струн любого струнного музыкального инструмента, будем иметь в виду частоту f 1 основного тона. Однако колебания струн содержат также гармоники, частоты f n которых отвечают соотношению:
Таким образом, звучащая струна способна излучать целый спектр волн с кратными частотами. Амплитуды A n этих волн имеют зависимость от способа возбуждения струны, будь то смычок или молоточек. Эти амплитуды необходимы для придания музыкальной окраски звуку (тембру).
Музыкальные инструменты необходимо периодически настраивать.
Камертон – устройство для настройки музыкальных инструментов, состоящее из настроенных в резонанс деревянного акустического резонатора и соединенной с ним металлической вилки.
Удар молоточка по вилке вызывает возбуждение всей системы камертона с последующим звучанием чистого музыкального тона.
Биения
Разберем также такое явление, как биения.
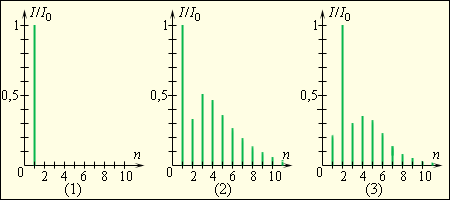
Биение – это явление, возникающее, когда две гармонические волны с близкими, но все же имеющими отличия частотами, накладываются друг на друга.
Для удобства примем, что амплитуды колебаний звуковых давлений являются одинаковыми и равны p 0 = A 0 0.
Согласно принципу суперпозиции полное давление, которое вызывается обеими волнами в каждый момент времени, есть совокупность звуковых давлений, задаваемых каждой волной в тот же момент времени. Запишем выражение, показывающее суммарное воздействие волн, используя тригонометрические преобразования:
Период биений Т б – это минимальное значение интервала между двумя моментами времени, которым соответствуют максимальная и минимальная амплитуда колебаний.
Формула, которая определяет медленно изменяющуюся амплитуду A результирующего колебания, имеет запись:
f б есть частота биений, определяемая как разность частот Δ f двух звуковых волн, которые воспринимаются ухом одновременно.
Гармонические колебания
На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

АЧХ шума.
Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).
Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.
Пару слов о матчасти
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания
Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:
где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:
ω=2 πf, где f — частота в Герцах.
Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.
Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал
Его сумма будет представлена следующей формулой:
Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.
Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.
Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)
Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.
Переходим к практическим упражнениям!
Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).
Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.
Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.
Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут
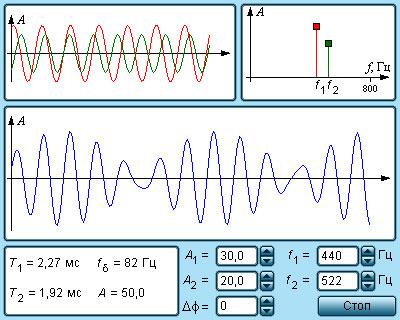
Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:
Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).
В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус
Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра
Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.
В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.
Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой с блекджеком и шлюхами, тем более, что это несложно.
Пишем свой анализатор спектра
Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.
Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.
Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.
Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек вектора исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.
Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.
Для начала алокируем массивы:
Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).
Массив для быстрого преобразования Фурье должен представлять собой последовательность
Что такое звук?
Любой человек, который учился (или учится) в школе, без особых размышлений ответит на этот вопрос так: «звук — это волна». И будет совершенно прав. А вот при попытке объяснить, что же из себя представляет эта волна, большинство людей вспоминает пример с веревкой или волнами на поверхности воды и после этого надолго задумываются.
Так что же представляет из себя звук? Любой предмет, совершающий возвратно-поступательные движения (камертон, струна рояля или гитары, наши голосовые связки и т.д.), вызывает в воздухе попеременное уменьшение или увеличение плотности. Движения одних молекул воздуха передаются другим молекулам, в результате чего в пространстве распространяются периодически повторяющиеся зоны увеличения и уменьшения плотности. Они-то и представляют из себя звуковую волну.
Если мы в каком-то месте поставим прибор, способный реагировать на изменение плотности воздуха, запишем его показания в течение некоторого времени и составим график зависимости плотности от времени, то получим кривую, близкую к синусоиде, знакомую нам по школьным учебникам физики. Именно такие колебания и улавливаются нашим ухом, в результате чего мы получаем ощущение звука.
Амплитуда, частота, длина и фаза звуковой волны
Амплитудой звуковой волны называется половина разницы между самым высоким и самым низким значением плотности. На графике амплитуде будет соответствовать разница между самой высокой (или низкой) точкой волны и горизонтальной осью графика. Частотой звука называют количество периодов, помещающихся в одной секунде. 1 Герц — это 1 период за секунду. Расстояние между областями одинакового сжатия воздуха называется длиной звуковой волны.
Поговорим более подробно о высоте звука. Наши уши устроены таким образом, что когда мы слышим два звука, частоты которых относятся как 2:1, то нам кажется, что эти звуки близки друг к другу и при одновременном воспроизведении они для нас как бы сливаются. Именно на этом эффекте основана музыкальная шкала высоты звуков, у которой одна и та же нота повторяется каждую октаву. То есть в натуральном звукоряде частоты одинаковых нот соседних октав соотносятся между собой как 2:1.
Звукорежиссерам часто приходится переводить значения частоты в ноты и обратно. Такие навыки могут понадобится, например, при работе с разными устройствами корректировки звука. Поэтому постарайтесь запомнить это соотношение — с помощью нехитрой математической операции теперь вы сможете вычислять частоту любой ноты, памятуя, что нота Ля первой октавы имеет частоту 440 Гц.
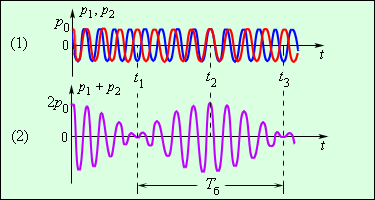
Но помимо высоты звука, мы способны достаточно точно определять положение звукового источника в пространстве. Это означает, что звуковые волны должны обладать свойством, на которое реагирует наш слуховой аппарат. Все объясняется достаточно просто: наши уши отнесены на некоторое расстояние друг от друга. То есть, звук в каждое из них поступает не в одно и то же время, а в разное. По задержке попадания одной и той же звуковой волны на барабанные перепонки мы и определяем пространственное положение источника звука (на самом деле есть еще несколько факторов, помогающих определять направление на звуковой источник, частично они упоминаются ниже). Для описания относительных временных свойств двух звуковых волн (или разных частей одной волны) вводится понятие фазы звуковой волны.
Посмотрите на рисунок выше. На первом графике показаны две волны, которые полностью совпадают друг с другом. В этом случае говорят, что волны находятся в фазе. На третьем графике в том месте, где у одной волны находится область высокой плотности, у другой — область низкой плотности. В этом случае говорят, что волны находятся в противофазе. При этом, если волны одинаковые, происходит их взаимное уничтожение (в природе это бывает крайне редко, чаще противофазные волны при наложении сильно искажают звук). Средний график показывает некое промежуточное положение. В этом случае говорят, что фаза одной волны сдвинута относительно другой.
Из всего вышесказанного становится понятно, что наш слух при определении пространственного положения источника звука реагирует именно на фазу волны. А по изменению фаз мы можем судить и о перемещении источника звука. В звукозаписи понятие фазы достаточно важно.
Уровень и громкость звука
Теперь немного поговорим о таком важном параметре как уровень звука. Любая звуковая волна, которая распространяется в пространстве, может оказывать на встречающиеся препятствия (в том числе и на наши барабанные перепонки) некое давление. Люди, которые бывали на концертах и стояли около мощных колонок, не понаслышке знают, что оно может быть очень сильным. Мы субъективно воспринимаем изменение давления звуковых волн в виде ощущения изменения громкости звука.
Максимальное изменение давления в воздухе при распространении звуковых волн по сравнению с давлением при отсутствии волн называется звуковым давлением. Как и любое другое, звуковое давление измеряется в Паскалях (Па). Но в акустике, при оценке интенсивности звуковых волн чаще применяется другое понятие — сила звука. Оно показывает поток звуковой энергии, который каждую секунду проходит через квадратный сантиметр условной плоскости, расположенной перпендикулярно направлению распространения волны.
Звуковое давление и сила звука находятся в квадратичной зависимости. То есть, сила звука = звуковое давление в квадрате. Сила звука описывает энергетические свойства самой волны и измеряется в ваттах/квадратный сантиметр (Вт/кв.см.). Такая единица бывает очень удобна при некоторых расчетах — это единственная причина ее введения.
Для того, чтобы мы смогли услышать тот или иной звук, его сила должна быть больше определенного уровня. Этот уровень называется порогом слышимости. То есть, если звуковая волна имеет малую интенсивность — ниже этого порога, мы просто не воспринимаем ее, и нам кажется, что вокруг стоит полная тишина, хотя на самом деле воздух вокруг колеблется. Точно также дело обстоит и со звуками большой интенсивности — мы слышим звук только до определенного уровня, который называется болевым порогом. Если сила звука больше этого уровня, то мы испытываем боль в ушах. Разница между уровнями болевого порога и порога слышимости называется динамическим диапазоном слуха. Мы способны воспринимать изменения силы звука в огромных пределах: сила звука болевого порога превосходит силу звука порога слышимости в тысячу раз!
Изменение уровня звука обычно оценивается в децибелах относительно порога слышимости. Когда говорят, что уровень звука в колонках равен ста децибелам, подразумевают, что колонки работают на уровне, превышающем порог слышимости на 100 дБ. Децибел — это логарифмическая единица измерения уровня звука, показывающая минимально слышимое изменение громкости. А динамический диапазон нашего слуха (разница между самым тихим и самым громким воспринимаемым звуками) составляет 120 дБ. Для того, чтобы как-то почувствовать такой непростой способ измерения уровня звука (лишь отражающий парадоксальность нашего слухового восприятия), мы приведем таблицу со знакомыми вам звуковыми объектами и уровнями звука, которые они производят.
Последняя строчка таблицы показывает уровень звука, превышающий болевой порог. Поэтому никогда не пытайтесь послушать звук барабана прямо у мембраны — ощущения будут очень неприятные. Из всего сказанного вы должны вынести хотя бы приблизительное представление о том, что такое децибелы. Если вы никогда не работали со звуковой техникой, то вряд ли в теории сможете проникнуться значимостью этой единицы измерения. И только когда вы начнете записывать свой собственный материал, глядя на индикаторы уровней, все до единого показывающие уровень в децибелах, вы сможете почувствовать суть логарифмической шкалы.
Теперь давайте более подробно поговорим о громкости звука — нашем субъективном ощущении от звуковых волн, имеющих разный уровень (звуковое давление, силу). Наше ощущение громкости во многом зависит от частоты звука. Высокие и низкие звуки, имеющие одинаковый уровень, субъективно воспринимаются нами как звуки разной громкости. А значение уровня звука и субъективно слышимой громкости совпадают только на частоте 1000 Гц.
На основании исследований человеческого слуха были построены графики, которые известны каждому звукорежиссеру как кривые равной громкости. На них изображены линии (они расположены через 10 дБ на частоте 1000 Гц), которые соответствуют одинаково воспринимаемой громкости на разных частотах.
Легко можно видеть, что мы гораздо лучше слышим на средних частотах, а на низких и высоких — чувствительность слуха притупляется. Из графика кривых равной громкости следует важный для практической деятельности вывод. Посмотрите на рисунок — наиболее линейно мы воспринимаем звук при уровнях 80-90 дБ. То есть при таких уровнях громкости наши уши наиболее адекватно передают звуковую картину. Поэтому корректировку звучания лучше всего делать при достаточно высокой громкости акустических систем — 80-90 дБ (примерно такой же уровень имеет шум в вагоне метро).
Тембр звука
Гитарист может извлекать из своего инструмента высокие и низкие, громкие и тихие звуки. Но что гитару делает гитарой? Почему ее звук отличается от звука фортепиано? Все объясняется довольно просто: реальные звуки представляют из себя созвучия, состоящие из нескольких простых волн. От комбинаций этих волн и зависит тембр инструмента.
У каждого созвучия есть основной тон — волна определенной частоты, которая имеет наибольший уровень. Например, у ноты Ля первой октавы эта волна имеет частоту 440 Гц. Но вместе с ней звучат и другие волны, частота которых в 2, 3, 4 раза и т.д. выше, чем у основного тона. В музыке они называются обертонами. В акустике принята немного другая терминология. И основной тон, и обертона называются гармониками и имеют порядковый номер в зависимости от высоты: основной тон — первая гармоника, первый обертон — вторая гармоника и т.д. Эквалайзеры работают по принципу понижения или повышения уровня тех или иных частотных полос, то есть с их помощью можно менять уровень тех или иных гармоник и, соответственно, изменять тембр.