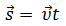Как построить график зависимости физика

Построение графиков в курсе физики на основе функциональной заивисимости

Разделы: Физика

Он используется в физике для формирования и анализа изучаемых физических понятий путем раскрытия их связей с другими понятиями, для решения задач обобщения, систематизации знаний.

Чаще всего при построении графиков на зависимость одних величин от других учащиеся запоминают вид графика, не вдаваясь в подробности, почему он проходит именно так, а не иначе. Когда зависимостей накапливается достаточно много, начинаются ошибки в построении графиков. В своей работе при построении графиков на различные зависимости физических величин я использую функциональный подход. В школьном курсе физики для построения графиков используются всего семь функций. Почти все физические величины положительные, поэтому графики функций будем рассматривать только в первой четверти.

№	Название функции	График
Прямая пропорциональность y = k x
Линейная y = k x + b
Обратная пропорциональность y = k\x
Показательная y = k a x
Функция y =
Квадратичная функция y = ax 2 + b x + c, y = ax 2
Тригонометрическая функция y = k sin x

Графики этих функций учащиеся изучают в курсе математики. Они знают эти графики либо умеют их строить по точкам. Моя задача сводится к тому, чтобы научить учащихся в физической формуле увидеть зависимость, определить ее вид, а затем установить соответствующий график.

Покажу это на примере:

Пример № 2. Необходимо построить график зависимости силы тока от сопротивления, которая выражена зависимостью I = . В донном примере изменяться будет сопротивление и в зависимости от него сила тока, а напряжение будет величиной постоянной. Сделаем следующие замены I = y; U = k; R = x; Получим функцию y = k\ x, графиком которой является ветвь гиперболы

План действий при построении графика физической зависимости:

Записываем аналитическое выражение данной зависимости (Формулу)

Устанавливаем, какие величины являются постоянными, и представляем их в виде коэффициента.

Источник

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении

Цели урока:

обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения за­дач закрепить полученные знания на практике;

развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;

воспитывающая: воспитание дисциплины и норм поведения, творческого от­ношения к изучаемому предмету; стимулировать активность учащихся.

Методы:

наглядный — видеоурок, записи на доске;

контролирующий — тестирование или устный (письменный) опрос, решение задач).

Связи:

межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;

внутрипредметные: равномерное и равноускоренное движение.

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

3. Объяснение нового материала.

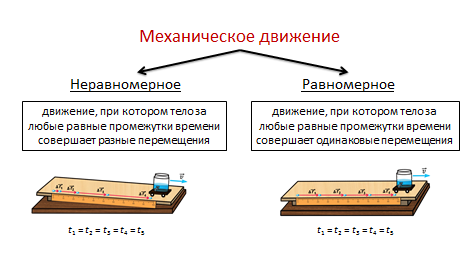
Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.

Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.

Если движение равномерное, то:

1. Скорость тела не меняется с течением времени;

2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;

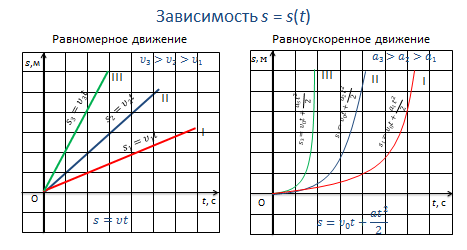
3. Уравнение перемещения имеет вид:

4. И — кинематическое уравнение равномерного движения.

1. Ускорение тела не изменяется с течением времени;

2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло

3. Уравнение скорости для равноускоренного движения имеет вид:

4. — уравнение перемещения для равноускоренного движения;

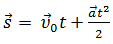
5. — кинематическое уравнение равноускоренного движения.

Для большей наглядности движение можно описывать с помощью графиков.

Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.

Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.

Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат — тоже в соответствующем масштабе — значения скорости тела, то мы получим график скорости.

Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.

Такие графики показывают, как изменяется скорость с течением времени, как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.

По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего — в случае движения тела в отрицательном направлении.

Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.

Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.

При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v₀ + at, скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.

По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.

При этом проекция перемещения для первого тела будет положительной.

Для второго тела, прямоугольного треугольника — половине произведения его катетов. В нашем случае, катеты — это время и конечная скорость тела.

Проекция перемещения — отрицательна.

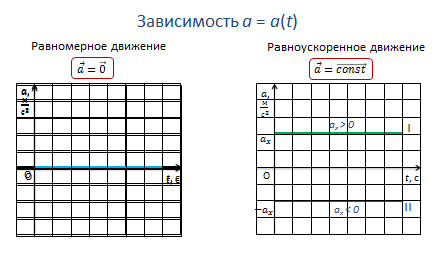
Теперь рассмотрим зависимость пройденного пути от времени.

Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат — путь.

Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.

При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.

При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.

Теперь перейдем к рассмотрению зависимости перемещения от времени.

Рассмотрим равномерное движение.

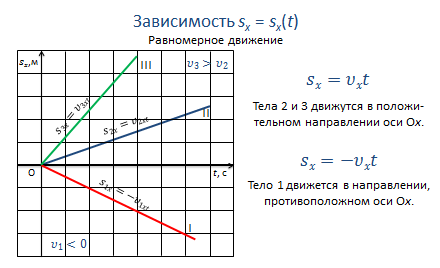
Т.к. при равномерном движении перемещение линейно зависит от времени (s_x = υ_xt), то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.

Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго.

А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.

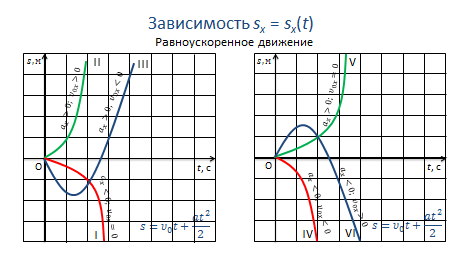
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.

Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.

Для 2-го тела ускорение и начальная скорость тела больше нуля.

Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.

У 4-го тела начальная скорость и ускорение меньше нуля.

Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.

И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.

И последнее, что мы с вами рассмотрим — это зависимость координаты тела от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).

Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.

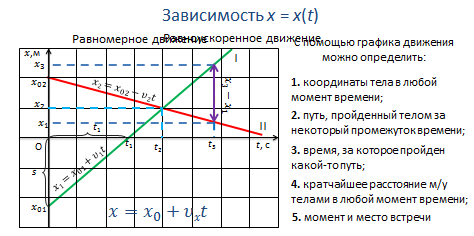
График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.

В случае прямолинейного движения тела графики дви­жения дают полное решение за­дачи механики, так как они позволяют найти поло­жение тела в любой момент времени, в том числе и в моменты времени, предшество­вавшие начальному моменту (если предполо­жить, что тело двигалось с такой же ско­ростью и до начала отсчета времени).

С помощью графика движения можно определить:

1. координаты тела в любой момент времени;

2. путь, пройденный телом за некоторый промежуток времени;

3. время, за которое пройден какой-то путь;

4. кратчайшее расстояние м/у телами в любой момент времени;

5. момент и место встречи

По виду графиков зависи­мости координаты от времени можно судить и о скорости дви­жения. Ясно, что скорость тем больше, чем круче график, чем больше угол между ним и осью времени (чем больше этот угол, тем больше изме­нение координаты за одно и то же время).

При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

4. Этап обобщения и закрепления нового материала

И так, сделаем главный вывод.

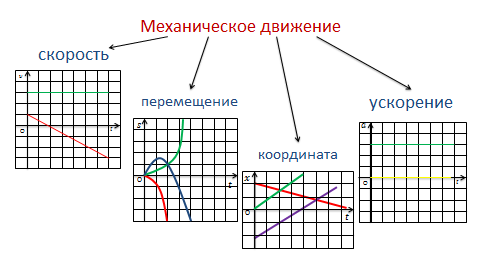
Механическое движение для большей наглядности можно описывать с помощью графиков:

1) Зависимости скорости от времени;

2) Зависимости ускорения от времени;

3) Зависимость координаты тела от времени;

4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

Источник

Как построить график зависимости физика

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

V_x — Скорость тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

a_x — Ускорение тела

t — Время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения: v_x = v_xo + a_xt

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

S_x — Перемещение тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

V_x — Скорость тела при равноускоренном движении по прямой

a_x — Ускорение тела

t — Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:

В координатах зависимость имеет вид:

Источник

Построение графиков движения с помощью Microsoft Office Excel по физике

Исследовательская работа по физике

ПОСТРОЕНИЕ ГРАФИКОВ ДВИЖЕНИЯ С ПОМОЩЬЮ

Автор: Бойко Дмитрий, 10 класс, МБОУ СОШ № 27 Муниципального образования Темрюкский район

Физический закон и его математическое выраже­ние неотъемлемая, фундаментальная часть изучения физики. Между буквами, обозначающими физические параметры, и математическими знаками существует функциональ­ная зависимость, в которой проявляют­ся причинно-следственные связи между величинами, объединёнными в формулу, и вложен глубокий физический смысл этих величин.

При подготовке к ЕГЭ по физике, первое задание по механике очень часто представлено в виде графиков. Нередка ситуация, когда ученик хорошо справля­ется с расчётными задачами, но оказывается беспо­мощным при решении графических задач, при ана­лизе сущности явления или закона, представленных формулой или графиком, из-за того, что качественные связи в законе не были им изучены или не поняты.

На помощь приходит графический метод обучения физи­ке. Исполь­зование графиков является одним из условий сознательного усвоения учебного материала, выра­ботки более чёткого понимания физических законов. Графическое представление физического процесса делает его более наглядным и тем самым облегчает понимание рассматриваемого явления, способст­вует развитию абстрактного мышления, интуиции, умения анализировать и сравнивать, находить более рациональный способ решения задач. Вопрос об ис­пользовании графиков становится всё более актуаль­ным, т. к. контрольно-измерительные материалы ЕГЭ по физике содержат до 25% графических заданий. Кроме того, применение графического ме­тода способствует укреплению связей физики с ма­тематикой, наполняет абстрактные математические закономерности конкретным физическим содержа­нием.

Я решил провести исследование, насколько результативными будут ответы учащихся, если на уроках применять методику построения простейших графиков и чтение графиков для равномерного (7 класс) движения и равноускоренного движения (10 класс).

Цель и объект исследования:

Создание и применение методики построения графиков движения при помощи программного обеспечения Microsoft Office Excel. Решение учащимися разработанных графиков.

Проблемой исследования является, применение новых информационно-коммуникационных технологий на уроках физики и повышение качества успеваемости учащихся, через знакомство с материалами и результатами исследования.

-изучить и проанализировать литературу по данной теме;

-научиться пользоваться программным обеспечением Microsoft Office Excel ;

-разработать задания для учащихся 7 и 10 классов, провести проверочные работы, сделать анализ полученных результатов;

— разработать памятки для построения графиков для учащихся 7 класса

-разработать рекомендации учителю физики.

-собрать и обобщить предложенный материал для педагогов школы;

— использование программы Microsoft Excel для построения графиков и их интерпретации.

— анализ тестовых и графических заданий для учащихся 7 и 10 класса

-анализ и сопоставление результатов контрольных работ и срезов у учащихся школы во время изучения данного раздела физики.

Описание исследовательской работы.

I. Практические навыки в построение графиков в Excel.

Как построить график в Microsoft Office Excel? Рассмотрим процесс построения графика функции в Microsoft Office Excel. Открыть программу можно следующим способом, на главной странице компьютера выбрать:

— все программы, найти Microsoft Offi c e затем строчку Microsoft Offi c e Excel 2007, запустить программу.

Откроется окно, содержащие поле для внесения данных. Как видим, Excel представляет собой электронные таблицы, позволяющие производить широкий перечень вычислений.

Для построения графиков равномерного движения, напомним следующие формулы.

Формула пути, пройденного телом при равномерном движении:

где: — скорость движения, S – пройденный путь, t – время движения.

И скорости равномерного движения:

Для учащихся старших классов, сразу в ячейке В2 ставим аргумент, в ячейке С2 функцию. Забиваем в столбец B значения t так, чтобы нас устраивал выбранный временной отрезок движения. В ячейку C3 забьём формулу, которую собираемся строить, например, для скорости 2 м/с. Для примера рассмотрим функцию S = 2 ∙ t.

II. Построение графиков.

Чтобы построить полученный график нужно выделить наши полученные значения

В меню выбрать «Вставка», найти слово «Точечная»

Можно сделать из этого графика шаблон, который будет использоваться при следующих построениях, для этого в окне «Макет» находим и подписываем название основной горизонтальной и вертикальной оси, название диаграммы; значение скорости 2м/с.

Теперь мы имеем шаблон, в котором можно менять значения скорости, например υ = 5 м/с. Для этого нужно добавить ряд при построении графиков. Результат – два графика на одном поле.

Вывод: При увеличении значения скорости в графике зависимости пути от времени для равномерного движения меняется угол наклона, угол увеличивается.

вводим временные промежутки так, чтобы соединив точки подряд, получили график параболы, т. к. квадратичная зависимость между величинами х= f ( t² ), затем строим график «Точечный», точечная с гладкими кривыми.

Получили график х=2 ∙t +2 ∙t²

Вывод: Отрицательное значение начальной координаты смещает график на это значение позиций по оси у вниз.

Аналогично можно сравнить по изменению параметров скорости и ускорения.

Вот таким достаточно простым способом можно строить графики в Microsoft Office Excel. Сохраняя полученные шаблоны можно строить графики, выбрав нужные параметры части электронной таблицы, делать выводы, как влияют изменении набора аргументов функции.

III. Приемы работы с графиками.

Можно учителю предложить следующие приёмы работы с гра­ фиками, которые образуют целостную систему:

Ø работа с предложенными графиками,

Ø решение задач графическим способом,

Ø графическое отображение результатов измерений при выполнении лабораторных работ

Работая с графиками м ожно:

— определять функциональную зависимость между предложенными физическими величинами;

— находить по значению известной величины зна­чение неизвестной;

— объяснять особенности протекания физического процесса, для которого построен график;

— выявлять сходство и различия при сравнении графиков;

— составлять таблицу значений соответствующих физических величин по их графической зависимости;

— идентифицировать вид движения, для которого постро­ен график.

Все задачи, решаемые графически, можно условно разделить на несколько типов по методу решения:

Ø графическое решение уравнений (ответ даётся точками пересечения кривых);

Ø графическая оценка (определение условий, при которых наблюдается наибольшее или наименьшее физическое действие);

Ø графическое интегрирование (ответ даётся вели­чиной площади фигуры, ограниченной кривой, орди­натами крайних точек и осью абсцисс);

Источник