Как построить график волновой функции
Как построить график волновой функции
3.1.2 Волновое уравнение. Квантовомеханическое объяснение строения атома
Неопределенность установления положения и скорости электрона столь велика, что необходимо вообще отказаться от анализа траектории его движения. Однако есть возможность вероятностного описания строения атома.
E – полная энергия электрона;
б) Побочное, или орбитальное, квантовое число ( l ). В спектрах многоэлектронных атомов наблюдается мультиплетная структура линий, т.е. линии расщеплены на несколько компонент. Мультиплетность линий означает, что энергетические уровни представляют собой совокупности энергетических подуровней, т.к. любой линии в спектре отвечает переход электрона из одного состояния в другое. Энергетические различия в состоянии электронов в данном уровне связаны с различием в форме электронных облаков.
Рисунок 3.1 – График волновой функции s-электрона в зависимости от расстояния до ядра. Форма s-орбитали
Рисунок 3.2 – График волновой функции p-электрона. Форма p-электронного облака
Знаки “+” и “–” от носятся не к вероятности нахождения электрона (она всегда положительна и равна | Ψ | 2 ), а к волновой функции, которая в разных частях электронного облака имеет различный знак.
в) Магнитное квантовое число ( ml ). Если атом поместить во внешнее магнитное поле, то происходит дальнейшее расщепление спектральных линий. Это означает, что при данных значениях n и l может существовать несколько состояний электрона с одинаковой энергией. Такие энергетические состояния называются вырожденными. Вырождение исчезает при воздействии на атом внешнего магнитного поля, что и приводит к появлению новых линий в спектре.
На рисунке 3.3 показано постепенное усложнение представлений о структуре электронной оболочки атома (от уровней к подуровням и далее к орбиталям ).
Рисунок 3.3 – Эволюция представлений о строении электронной оболочки атома. Энергетическая диаграмма уровней с 1-го по 3-й
Пользуясь принципом Паули, можно подсчитать, какое максимальное число электронов может находиться на каждом подуровне, т.е. определить емкость подуровней:
Здесь электроны на орбиталях изображены стрелками, направленными вверх или вниз в зависимости от знака спинового квантового числа.
Как построить график волновой функции
Библиографическая ссылка на статью:
Дангян А.Э. Волновая функция электрона // Современные научные исследования и инновации. 2016. № 1 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2016/01/62782 (дата обращения: 18.12.2021).
Введение
Основным уравнением, из которого вытекала гипотеза Луи де Бройля о волновых свойствах материи, была формула, записанная им на основании гипотезы Планка о наименьшем кванте энергии и уравнения Эйнштейна, связывающего массу и энергию, 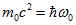
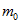
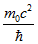
Применение гипотезы де Бройля к элементарным частицам, в частности к электрону, будет означать, что электрон содержит внутренний волновой процесс. Но в свое время этот волновой процесс не был обнаружен и волны де Бройля стали ассоциироваться только с механическим движением частиц.
Современная физика интерпретирует волны де Бройля как волны вероятности, не имеющие материального воплощения.
В последнее время, появились экспериментальные факты, подтверждающие первоначальную гипотезу де Бройля о существовании волн материи [3], [4].
Эти экспериментальные результаты стимулировали появление многочисленных попыток теоретического объяснения [7], [8].
В настоящей работе, путем решения релятивистского уравнения М2 [2] будет показано, что элементарные частицы, в частности электрон, вполне могут содержать волновой процесс с весьма специфическими свойствами. Волновая модель неподвижного электрона представляется в виде сферического волнового процесса.
Нестационарное уравнение М2
Преобразуем полученное в работе [2] стационарное релятивистское уравнение М2 (1.1) в нестационарную форму.
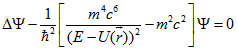
Для этого удаляем из уравнения потенциальную энергию 
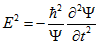
В результате получим: 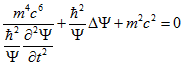
Теперь необходимо найти дисперсионное соотношение для полученного уравнения (1.2).
Для этого подставим сферическую волну 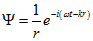
Определим второе производное по времени: 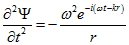
Оператор Лапласа в сферической системе координат имеет следующий вид:
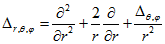
Определим результат действия оператора Лапласа на сферическую волну:
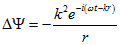
В результате получим дисперсионное соотношение в виде: 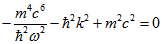
Волна без дисперсии и волновой пакет без расплывания
Для полученного дисперсионного соотношения, определим фазовую и групповую скорости распространения волн.
Как известно фазовая скорость определяется через круговую частоту 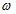
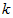
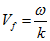
Из уравнения (1.7) определим круговую частоту .gif)
.gif)
Подставим полученное значение (2.2) в формулу (2.1) 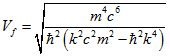
Групповая скорость определяется по формуле: 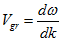
.gif)
Построим графики зависимости фазовой и групповой скоростей от волнового числа 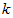
Рис.1 График зависимости фазовой скорости 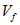
.gif)
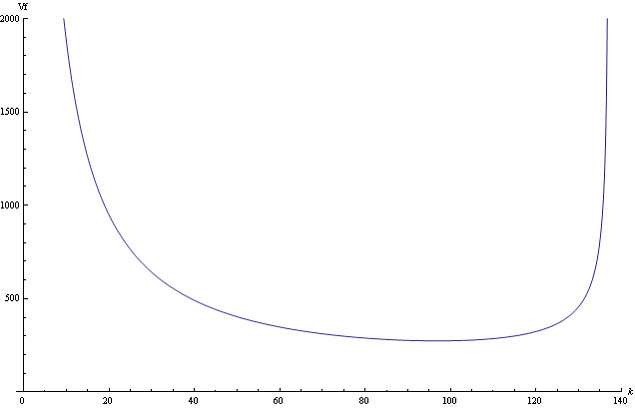
Рис.2 График зависимости групповой скорости 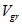
.gif)
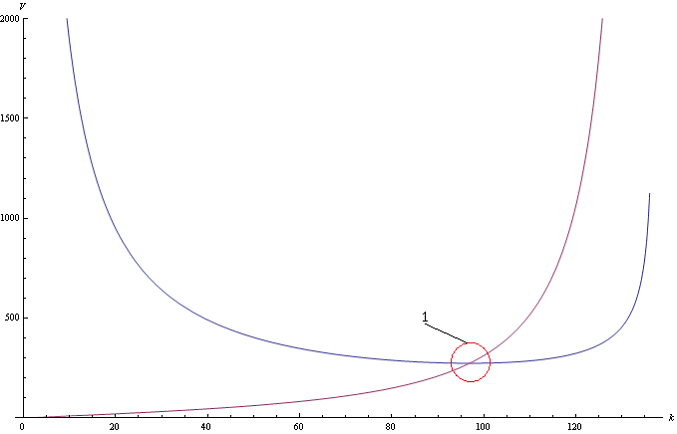
Теперь совместим оба графика на одном рисунке.
Рис.3 Совместный график фазовой и групповой скоростей.
Как можно заметить, при определенном значении волнового числа, фазовая скорость равняется групповой скорости.
Приравнивая соответствующие формулы 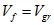
.gif)
.gif)
.gif)
Полученное значение скорости в два раза выше скорости света. Но это не скорость движения электрона. Так как мы рассматриваем электрон в неподвижном состоянии. Это скорость распространения в пространстве сферической волны де Бройля (для первоначальной версии гипотезы), то есть волны материи. И поскольку полученная волна материи пока что имеет неизвестную природу, то пока не будем ограничивать ее характеристики и в частности скорость распространения.
Прежде чем продолжить, обратим внимание на следующее обстоятельство. Определим энергию покоя электрона в соответствии с формулой 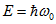
.gif)
.gif)
.gif)
Для устранения полученного несоответствия, введем понятие затравочной массы электрона. Которая вступая во внутренние волновые процессы, образует энергию покоя .gif)
.gif)
Тогда окончательно получим для устойчивого состояния значение волнового числа .gif)
.gif)
Интегрируя сферические волны в небольшой окрестности .gif)
.gif)
Теперь, после получения параметров устойчивого состояния электрона, имеет смысл перейти к стационарному уравнению и окончательно получить волновую функцию голого неподвижного электрона.
Для этого, подставим полученное значение затравочной массы 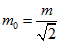
.gif)
.gif)
Полученное уравнение, в теории дифференциальных уравнений, известно как уравнение Гельмгольца.
Решение уравнения Гельмгольца
Для решения уравнения (2.11) применим стандартную методику разделения переменных в сферической системе координат.
Представим волновую функцию в виде произведения радиальной и угловой частей .gif)
Оператор Лапласа в сферических координатах выглядит следующим образом: .gif)
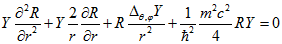
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
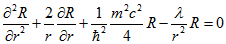
.gif)
.gif)
.gif)
.gif)
.gif)
Умножив уравнение (3.8) на дробь 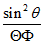
.gif)
.gif)
.gif)
.gif)
.gif)
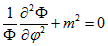
Решение .gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
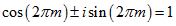
.gif)
.gif)
.gif)
.gif)
Для решения .gif)
Решение дает: .gif)
То есть, решением является, сумма присоединенных функций Лежандра первого и второго рода.
Сделаем обозначение .gif)
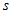
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
Поскольку у нас электрон находится в неподвижном состоянии, то обычные условия квантования орбитального момента не имеют места. Поэтому пока не можем говорить, что квантовое число .gif)
.gif)
.gif)
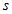
.gif)
.gif)
.gif)
.gif)
Приведем для наглядности несколько графических примеров угловой части волновой функции при различных значений квантовых чисел .gif)
.gif)





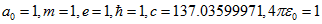
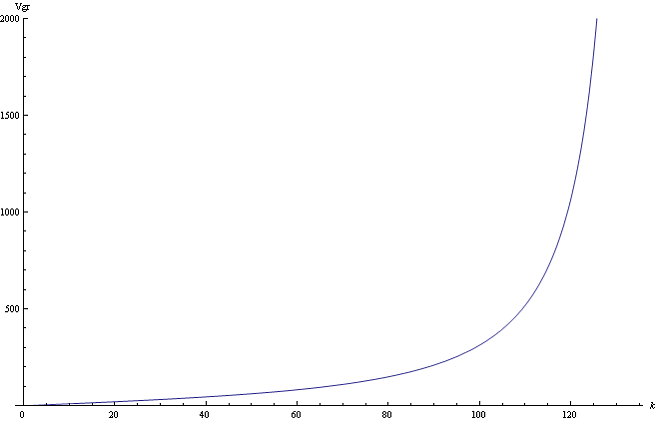

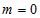
.gif)
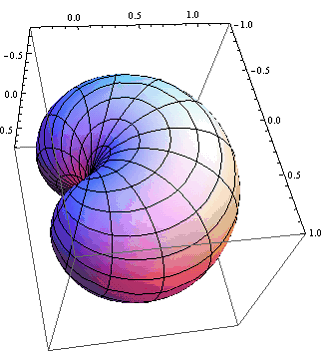
.gif)
.gif)
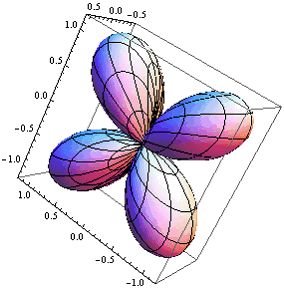
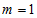
.gif)
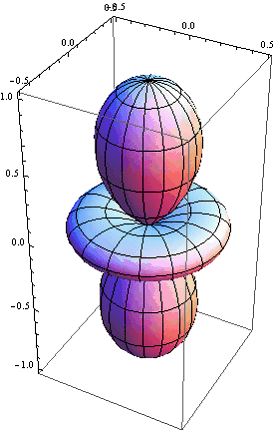
.gif)
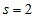
.gif) (3.18)
(3.18).gif) (3.19)
(3.19).gif) . Поэтому принимаем
. Поэтому принимаем .gif) . И окончательно радиальная часть волновой функции будет иметь вид:
. И окончательно радиальная часть волновой функции будет иметь вид:.gif) (3.20)
(3.20)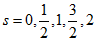 . Поскольку вопрос нормировки пока не обсуждаем, по приведенным причинам, то примем
. Поскольку вопрос нормировки пока не обсуждаем, по приведенным причинам, то примем .gif) . В единицах Хартри масса электрона
. В единицах Хартри масса электрона .gif) , постоянная Планка
, постоянная Планка .gif) и скорость света
и скорость света .gif) .
.
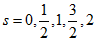
.gif)
.gif) (3.21)
(3.21)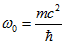 . Волновой процесс выходит в наружу и образует волны материи. При этом волновое число равно
. Волновой процесс выходит в наружу и образует волны материи. При этом волновое число равно .gif) , следовательно длина волны равна
, следовательно длина волны равна .gif) , а скорость распространения в пространстве двукратно превышает скорость света. Следовательно, волны материи имеют не электромагнитную природу.
, а скорость распространения в пространстве двукратно превышает скорость света. Следовательно, волны материи имеют не электромагнитную природу..gif) . Следовательно, полученная длина волны составляет двукратную величину Комптоновской длины волны
. Следовательно, полученная длина волны составляет двукратную величину Комптоновской длины волны .gif) . Отсюда можно сделать предположение, что Комптоновская длина волны связана с волновыми свойствами электрона.
. Отсюда можно сделать предположение, что Комптоновская длина волны связана с волновыми свойствами электрона..gif) . То есть, масса электрона формируется, в результате вступления затравочной массы во внутренний волновой процесс. По аналогии можно предположить, что и затравочная масса тоже образуется в результате волнового процесса второй ступени. И следовательно, материя имеет многоступенчатую, вложенную друг в друга волновую структуру, как матрешка.
. То есть, масса электрона формируется, в результате вступления затравочной массы во внутренний волновой процесс. По аналогии можно предположить, что и затравочная масса тоже образуется в результате волнового процесса второй ступени. И следовательно, материя имеет многоступенчатую, вложенную друг в друга волновую структуру, как матрешка..gif) . Область возможных значений квантовых чисел электрона еще предстоит изучать.
. Область возможных значений квантовых чисел электрона еще предстоит изучать.