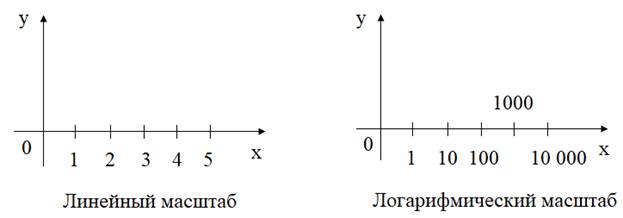
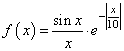Как построить график в логарифмическом масштабе
Делаем логарифмический масштаб у координатных осей
До сих пор мы с вами отображали графики в декартовой системе с линейным шагом изменения значений. Это довольно частый вариант, который используется в большинстве случаев. Но бывают функции, которые требуют логарифмического масштаба (изменения шага) по координатам.
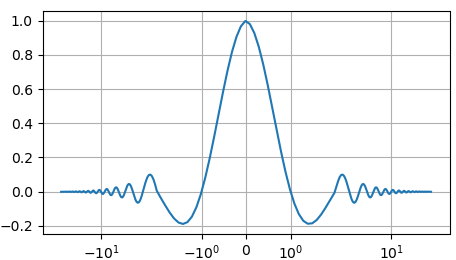
Например, если сформировать график функции:
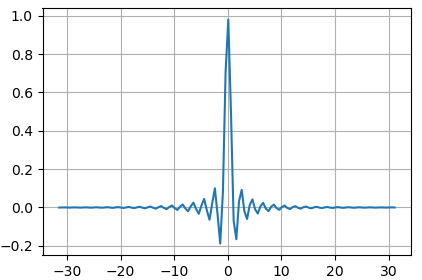
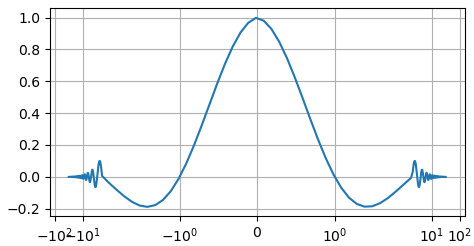
Если отобразить его в линейной системе координат:
То мелкие колебания функции на больших частотах будут не видны:
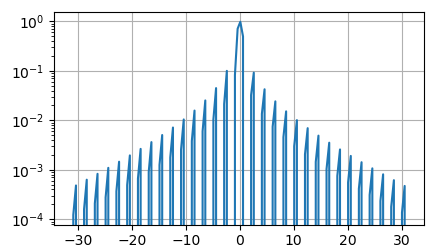
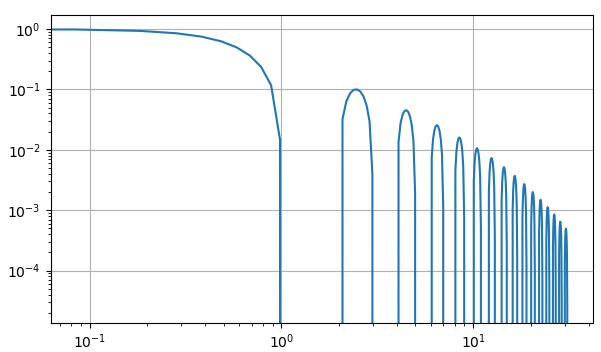
Как раз здесь может помочь логарифмический масштаб по оси ординат. Для этого достаточно воспользоваться методом semilogy(), чтобы по оси Oy откладывался логарифмический масштаб (логарифм по основанию 10) для графика:
В результате получим следующее построение:
Видите, стало гораздо информативнее и конечному пользователю показывается больше информации о сигнале.
Аналогично, можно формировать логарифмический масштаб по оси ординат с помощью метода:
Того же самого эффекта можно добиться и с помощью прежней функции plot(), только дополнительно указать логарифмический масштаб по нужной оси. Например, так:
Здесь был использован метод set_yscale() для изменения масштаба со значения ‘linear’ на значение ‘log’. По аналогии, можно изменить масштаб и для оси Ox с помощью метода set_xscale():
Как я только что отмечал, логарифмический масштаб формируется по основанию 10. Если нужно изменить и указать другое основание, то это делается с помощью параметра base:
Вернемся к нашему графику. Если на него внимательно посмотреть, то по вертикали дополнительно отложены небольшие риски. Это восемь промежуточных линейных значений. Например, между значениями
Откладываются риски со значениями:
0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2
Мы можем управлять их отображением, указав их значения в виде целых чисел в списке параметра subs:
Здесь мы указываем отображать риску со значением 0,2 или 0,02 или 0,002 и т.д. И риску со значениями 0,9 или 0,09 или 0,009 и т.д.
Рассмотрим далее возможность использования третьего параметра ‘symlog’. Мы его пропишем для оси Ox в следующем виде:
Здесь использован дополнительный параметр linthresh, определяющий граничное значение [-2; 2], где график следует отображать в линейном масштабе. А все, что выходит за эти пределы – в логарифмическом. В результате, получим такое построение:
Дополнительно линейный масштаб можно растянуть, указав масштаб в дополнительном параметре linscale:
Наконец, если нам нужно установить логарифмический масштаб по обеим осям, то проще всего для этого воспользоваться функцией loglog(), вместо функции plot() или semilogx()/semilogy():
Вот так, достаточно просто можно задавать и управлять логарифмическим масштабом при отображении графиков в пакете matplotlib.
Видео по теме
#1. Установка пакета и основные возможности
#2. Функция plot для построения и оформления двумерных графиков
#3. Отображение нескольких координатных осей в одном окне
#4. Граничные значения осей и локаторы для расположения меток на них
#5. Настраиваем формат отображения меток у координатных осей
#6. Делаем логарифмический масштаб у координатных осей
#7. Размещаем стандартные текстовые элементы на графике
#8. Добавляем легенду и рисуем геометрические фигуры на графиках
#9. Рисуем ступенчатые, стековые, stem и точечные графики
#10. Рисуем гистограммы, столбчатые и круговые диаграммы
#11. Показ изображений и цветовых сеток
#12. Как строить трехмерные графики
#13. Рисуем линии уровня функциями contour, contourf и tricontour, tricontourf
#14. Создаем анимацию графиков Классы FuncAnimation и ArtistAnimation
© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
П 4. Логарифмический масштаб
Построение графиков и пользование ими становится затруднительными, если величины, откладываемые вдоль координатных осей, изменяются очень в больших пределах. В этом случае используется логарифмический масштаб, позволяющий значительно расширить пределы изменения функций наносимых на график, без увеличения размеров чертежа. Для этого вдоль координатных осей откладывается вместо значений функций десятичные логарифмы этих значений, а полученным точкам присваиваются названия откладываемых значений. В результате применения логарифмического масштаба по одной из координатных осей кривизна графиков уменьшается, а зависимости, близкие к показательной функции, приближаются к прямым линиям.
Практическое построение координатной сетки логарифмического масштаба (рис. 5) осуществляется следующим образом. Одну или обе координатные оси разбивают на равные отрезки, каждый из которых соответствует увеличению в 10 раз. После этого каждый отрезок делят на девять неравных частей, откладывая от левого (или нижнего) конца отрезка 0,3; 0,47; 0,6; 0,7; 0,78; 0,85; 0,9 и 0,95 его длины.
Полученным точкам деления присваивают названия десятых долей отрезка.
Если по одной оси координат принят логарифмический масштаб, а по другой – обычный (линейный), то такую координатную сетку называют полулогарифмической (рис. 6).
|
|
В качестве примера использования логарифмического масштаба см. графики зависимостей ρ(N), приведенные в прил. 5.
П 5. графики Зависимостей удельного сопротивления от концентрации примесей для Si и Ge при 300 К
П 6. ЭКСПЕРИМЕНТАЛЬНЫЕ ЗНАЧЕНИЯ ВЫСОТЫ БАРЬЕРА ШОТТКИ φb, эВ ПРИ 300 К
П 7. графики зависимости разности работ выхода φms от уровня легирования кремниевой подложки для МДП-структур
П 8. Неперы и децибелы
В различных приложениях электроники часто приходится иметь дело с относительными величинами (коэффициент усиления или ослабления, превышение сигнала над помехой, уровни передачи, отсчитываемые от некоторого исходного уровня и т.д.). На практике оказалось удобным вместо отношений мощностей, напряжений и токов оперировать с логарифмами этих отношений.
Если используются натуральные логарифмы, то отношения напряжений и токов выражают в неперах по формулам
а отношение мощностей – по формуле
Эти числа называют относительными уровнями в неперах по напряжению ( 



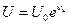


При использовании десятичных логарифмов отношения мощностей выражают в белах:
но чаще используют в 10 раз меньшую единицу, называемую децибелом (дб).
Для напряжения и тока при этом получается:
Для расчета напряжений, токов или мощностей в какой-либо точки цепи по известным их значениям в начале цепи (исходные уровни 
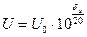


Непер и децибел следующим образом связаны друг с другом:
П 9. ТЕМЫ РЕФЕРАТОВ
1. Варизонные полупроводники и гетероструктуры.
2. Диагностика глубоких энергетических уровней в полупроводниковых структурах.
3. Емкостные методы контроля параметров полупроводниковых структур.
4. Квантовый эффект Холла в двумерном электронном газе.
5. Линейные дефекты в кремнии и их влияние на его электрофизические свойства.
6. Молекулярная электроника.
7. Наноэлектроника, наноэлектронные структуры и способы их формирования.
9. Проблемы полупроводниковой элементной базы на основе спиновых взаимодействий.
10. Проблемы одноэлектроники. Применение одноэлектрон-ных приборов.
11. Размерное квантование и квантово-размерные структуры.
12. Светодиоды (физика, конструкции, технология, рабочие характеристики).
13. Свойства и перспектива применения углеродных нанотрубок в электронике.
14. Сенсоры температуры на основе полупроводниковых структур.
15. Сенсоры давления на основе полупроводниковых структур.
16. Сенсоры газов на основе полупроводниковых структур.
17. Сенсоры влажности на основе полупроводниковых структур.
18. Сенсоры электромагнитных излучений на основе полупроводниковых структур.
19. Сканирующая зондовая микроскопия материалов и структур наноэлектроники.
20. Солнечные элементы на однородных и неоднородных p-n-переходах.
21. Солнечные элементы на поверхностных и тонкопленочных полупроводниковых структурах.
22. Физические и технологические ограничения традиционного направления развития микроэлектроники.
23. Физические проблемы надежности интегральных микросхем.
24. Физические проблемы создания нанотранзистора.
25. Фотодетекторы (фоторезисторы, фотодиоды, фототранзисторы).
26. Фотоэлектрические явления в квантовых ямах.
27. Функциональные магнитоэлектрические устройства.
28. Функциональные устройства на основе приборов с зарядовой связью.
29. Функциональные устройства на основе объемного отрицательного сопротивления.
30. Функциональные устройства на оптронах.
31. Функциональные устройства на поверхностных акустических волнах.
32. Функциональные устройства на тонкопленочных многослойных структурах.
33. Функциональные элементы и устройства на основе явления сверхпроводимости.
34. Электронные свойства неупорядоченных систем.
Построение графиков в логарифмическом и полулогарифмическом масштабах.
Если для одиночного графика диапазоны изменения переменных вдоль одной или обеих осей координат слишком велики, то можно воспользоваться функциями построения графиков в логарифмическом и полулогарифмических масштабах. Для этого предназначены функции semilogx (логарифмический масштаб по оси 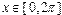
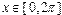
Построим в качестве примера график функции 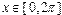
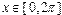
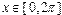
Будем иметь (рис. 2.9.6):
Рис. 2.9.6. График функции 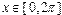
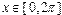
Построение графиков в полярных координатах.
Для построения графика функции в полярной системе координат используется команда polar, например (рис. 2.9.7):
Оформление графиков и графических окон
Функции построения графиков, рассмотренные в предыдущем параграфе осуществляли автоматическое оформление графиков. Разумеется у системы MATLAB имеются дополнительные возможности, связанные с управлением внешним видом графика – заданием цвета и стиля линий, а также размещение различных надписей в пределах графического окна.
Рис. 2.9.7. График функции 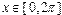
Рис. 2.10.1. Пример маркировки точек кривой посредством окружностей.
Выбор свойств линий.
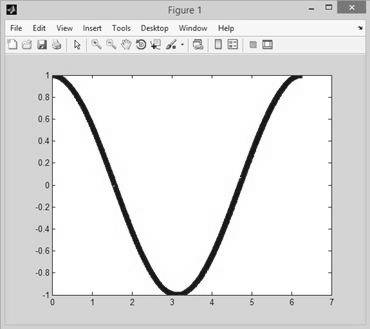
Так, например, команды (рис. 2.10.1)
позволяют придать графику вид черной сплошной линии, на которой в дискретных точках, расстояние между которыми равно 0.1, проставляются черные окружности. Здесь функция plot дважды строит график одной и той же функции, но в двух разных стилях. Первый из этих стилей отмечен как “k-”, что обозначает проведение линии черным цветом (буква k), а штрих означает проведение сплошной линии. Второй стиль, помеченный как “ko”, обозначает проведение тем же черным цветом (буква k) окружностей (буква o) на месте вычисляемых точек.
В общем случае команда
позволяет определить в одном графическом окне изображения нескольких функций y1(x1),y2(x2),… используя стили s1,s2,….
Заметим, что стили s1,s2,… задаются в виде набора трех символьных маркеров (стилевой строки), один из которых задает тип линии, второй – цвет линии, а третий – тип маркера, используемого для пометки представляемых точек (таблица 2.10.1). При отсутствии указания типов маркеров используются значения, установленные по умолчанию. Отметим, что порядок, в которым указываются маркеры, задающие тип линии, цвет линии и тип точки несущественен. Если в стилевой строке задан тип маркера, но не указан тип линии, то представляемые точки маркером метятся, но не соединяются друг с другом отрезками прямых.
Более мощным способом построения графиков функций является метод дескрипторов, который относится к низкоуровневой графике MATLAB. Метод дискрипторов позволяет напрямую обратиться к базовым графическим объектам и задать его свойства. Детальное знакомство со свойствами графических объектов MATLAB выходит за рамки книги.
В этой связи приведем ниже некоторый пример, иллюстрирующий основные приемы работы с дискрипторной графикой и позволяющий продемонстрировать суть данного метода (рис. 2.10.2).
В данном случае команда plot через опорные точки проводит отрезки прямых линий с координатами x,y. Прямые линии в системе MATLAB представляют собой объекты типа line. Эти объекты имеют очень большое количество свойств и характеристик, которые можно менять. Доступ к этим объектам осуществляется посредством их дескрипторов.
Командой hplot=plot(x,y) создается графический объект и переменной hplot присваивается значение дескриптора графического объекта типа line, использованного для построения графика функции 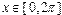
Таблица 2.10.1. Параметры для управления цветом и видом графиков.
| Параметр | Обозначение(управляющий символ) |
| Тип линии | |
| сплошная (по умолчанию) | — |
| пунктирная | : |
| штриховая | — |
| штрих-пунктирная | -. |
| Цвет линии | |
| красный (от англ. red) | r |
| желтый (от англ. yellow) | y |
| зеленый (от англ. green) | g |
| синий (от англ. blue) | b |
| голубой /циановый/ (от англ. cyan) | c |
| розовый /малиновый/ (от англ. magenta) | m |
| черный (от англ. black) | k |
| белый (от англ. white) | w |
| Тип маркера | |
| точка (жирная точка) | . |
| кружок | о |
| крестик (косоугольный крестик) | x |
| плюс (прямоугольный крестик) | + |
| звездочка (восьмиконечная снежинка) | * |
| квадратик | s |
| ромбик | d |
| отсутствие маркера | none |
| треугольник вершиной вниз | v |
| треугольник вершиной вверх | ^ |
| треугольник вершиной влево | |
| треугольник вершиной вправо | |
| пятиконечная звезда | p |
| шестиконечная звезда | h |
Затем данный дескриптор передается в качестве параметра функции set для опознания конкретного графического объекта и задания значений соответствующих свойств объекта.
В рассматриваемом примере было установлено значение свойства ‘LineWidth’ (толщина линии) равным 7 (по умолчанию 0.5). График, полученный в результате изменения толщины линии, представлен на рис. 2.10.2.
Текущее значение любого параметра (атрибута; характеристики) графического объекта возвращается функцией get. Так, например, если после получения показанного на рис. 2.10.1 графика выполнить команду
Рис. 2.10.2. График функции 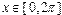
то для переменной width будет присвоено значение свойства ‘LineWidth’ равное 7.
Для получения списка всех свойств графического объекта следует обратиться к функции get, указав ей в качестве единственного параметра дескриптор объекта. Так, например, для дескриптора hplot объекта типа line можно найти весь список его свойств:
Как построить график в логарифмическом масштабе
Обычная графика MATLAB
Построение графиков точками и отрезками прямых
Графики в логарифмическоми полулогарифмическом масштабе
Гистограммы и диаграммы
Графики специальных типов
Создание массивов данных для трехмерной графики
Построение графиков трехмерных поверхностей, сечений и контуров
Средства управления подсветкой и обзором фигур
Средства оформления графиков
Одновременный вывод нескольких графиков
Управление цветовой палитрой
Окраска трехмерных поверхностей
Двумерные и трехмерные графические объекты
Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.
Описанию графических функций и команд посвящена обширная электронная книга в формате PDF. Объем материала по графике настолько велик, что помимо вводного описания графики в уроке 3 в этой книге даются еще два урока по средствам обычной и специальной графики. Они намеренно предшествуют систематизированному описанию большинства функций системы MATLAB, поскольку графическая визуализация вычислений довольно широко используется в последующих материалах книги. При этом графические средства системы доступны как в командном режиме вычислений, так и в программах. Этот урок рекомендуется изучать выборочно или выделить на него не менее 4 часов.
Построение графиков отрезками прямых
Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.
Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.
plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:
На рис. 6.1 показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.
Рис. 6.1. Графики двух функций в декартовой системе координат
plot(Y) — строит график у(г), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.
Вот пример использования команды plot(Y):
Соответствующий график показан на рис. 6.2.
Рис. 6.2. График функции, представляющей вектор Y с комплексными элементами
plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть следующие символы.