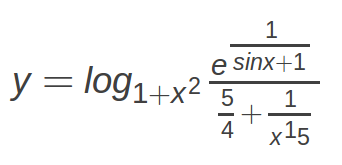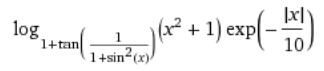Как построить график с погрешностями
Пострение графиков
Запись алгебраических выражений
Фундаментальная задача программирования — вычисление математических и, в частности, алгебраических функций. Казалось бы, что проще? Однако, запись выражения на языке математики не принимается напрямую языком программирования. Выражение нужно написать в виде, который будет понятен тому или иному языку программирования.
Упражнение №1
Запишите выражение, заданное формулой, в виде, подходящем для языка Python.
и найдите его значения в точках 1, 10, 1000.
Для вычисления математических функций мы не будем использовать стандартную библиотеку math. Т.к. она не работает с векторами. В нашем случае разумней обратить внимание на библиотеку numpy. Данная библиотека обеспечивает удобную работу с векторам.
Т.е., если у нас есть вектор x=[1, 2, 3, 4] и мы вызовим numpy.log(x), то логарифм будет взят от каждого элемента списка и возвращен будет список значений.
Аналогичная функция в модуля math ожидает число, т.е. нельзя сделать math.log(x), нужно делать math.log(x[0]) и т.д.
Традиционно библиотека numpy подключается командой:
Данный вызов сообщает, что подключить numpy под псевдонимом np. Это делается, чтобы не писать каждый раз:
Такой код, с более коротким именем библиотеки, элементарно, проще читать.
Основные математические функции и константы функии, которые нам понадобятся из numpy:
| Функция библиотеки math | Математическая функция |
|---|---|
| np.pi | Число pi |
| np.e | Число e |
| np.cos | Косинус |
| np.sin | Синус |
| np.tan | Тангенс |
| np.acos | Арккосинус |
| np.asin | Арксинус |
| np.atan | Арктангенс |
| np.exp | Экспонента |
| np.log | Логарифм |
Функция log вычисляет натуральный логарифм. Чтобы вычислить логарифм по другому основанию, нужно воспользоваться формулой перехода. Например, если мы хотим получить логарифм x по основанию 2, нужно написать:
Построение графиков
Пример построения графика функции:
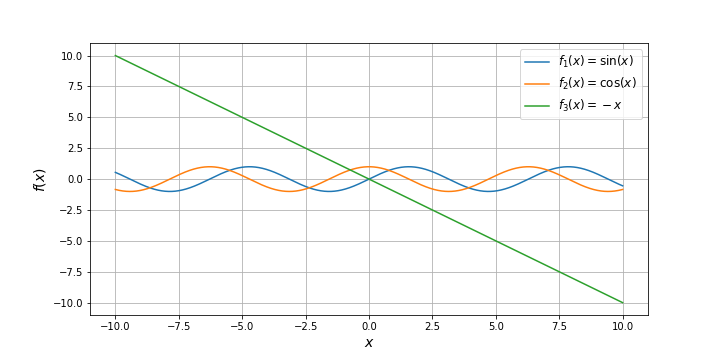
На одном рисунке можно построить несколько графиков функций:
Также довольно просто на график добавить служебную информацию и отобразить сетку:
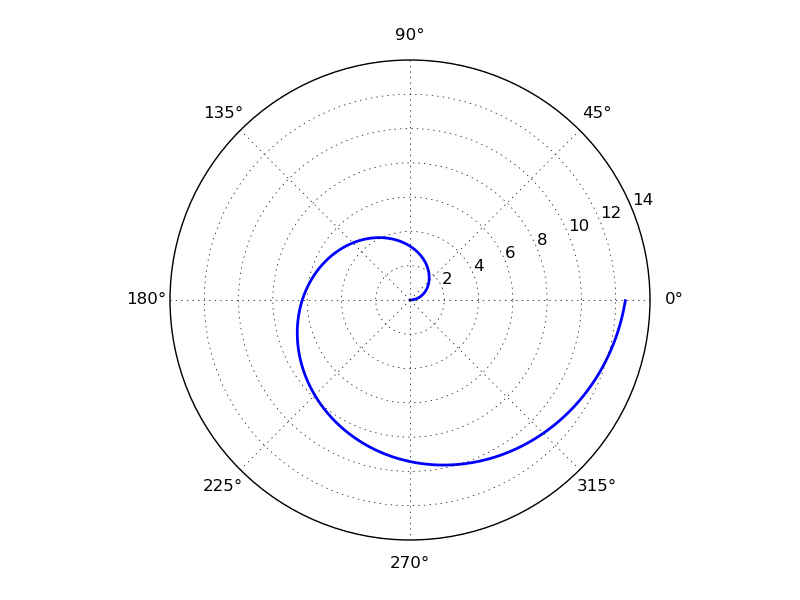
График может быть построен в полярной системе координат, для этого при создании subplot необходимо указать параметр polar=True :
Или может быть задан в параметрической форме (для этого не требуется никаких дополнительных действий, поскольку два массива, которые передаются в функцию plot воспринимаются просто как списки координат точек, из которых состоит график):
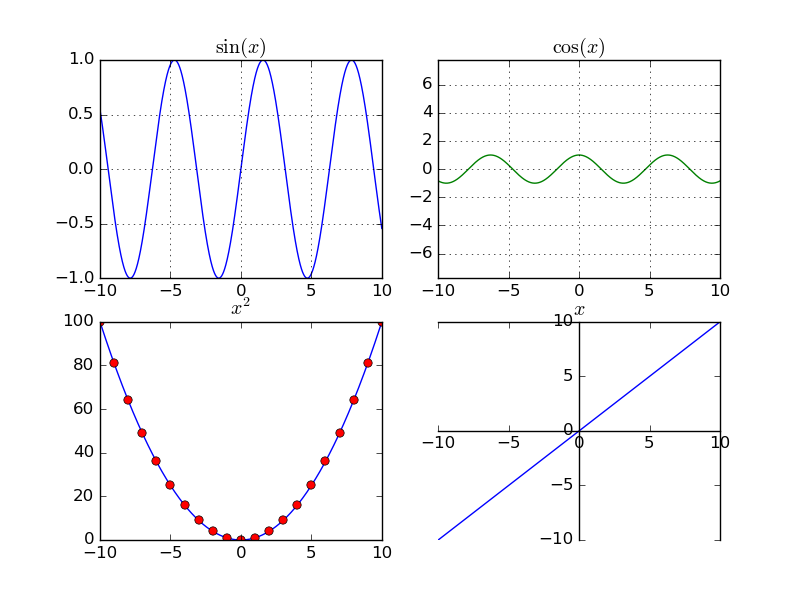
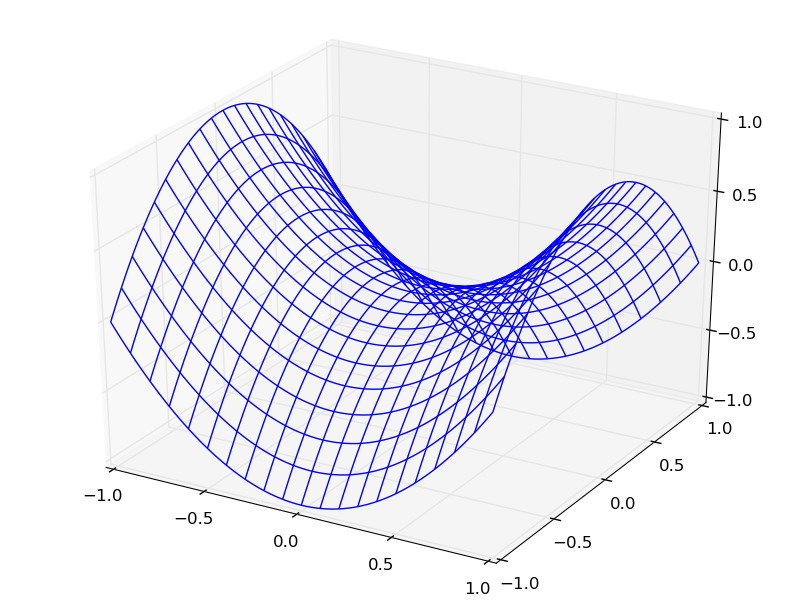
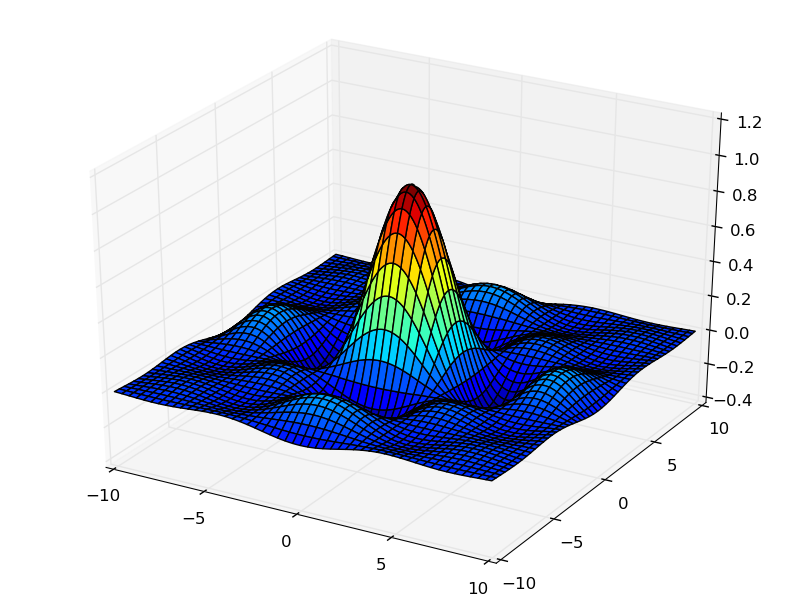
График функции двух переменных может быть построен, например, так:
Каждую последовательность можно отобразить своим типом точек:
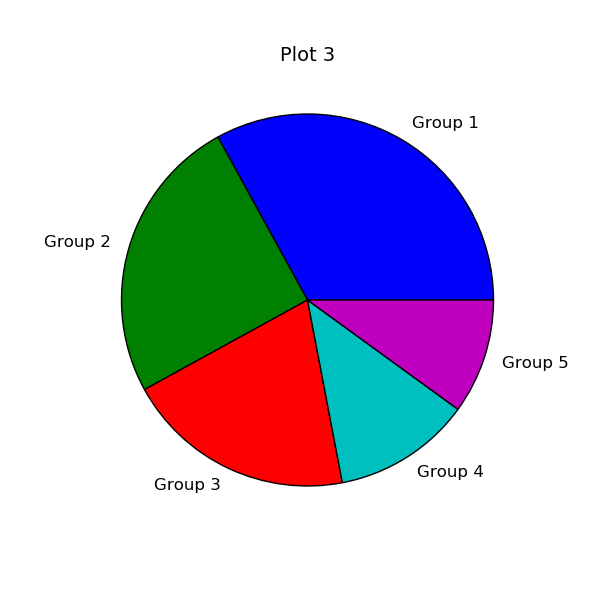
Также в matplotlib существует возможность строить круговые диаграммы:
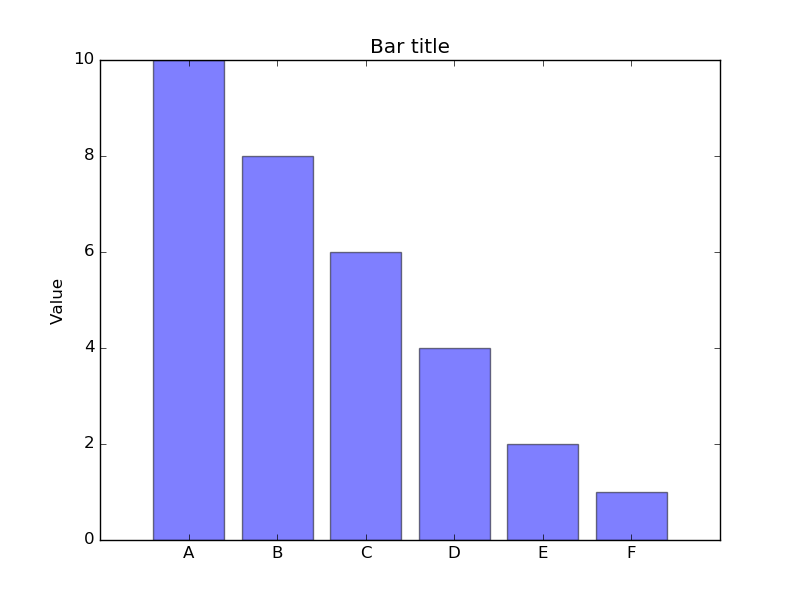
И аналогичным образом столбчатые диаграммы:
Функция eval()
Упражнение №2
Постройте график функции
и по графику найдите найдите корни уравнения y(x) = 0. (Не нужно применять численных методов — просто приблизьте график к корням функции настолько, чтобы было удобно их найти.)
Упражнение №3
Постройте график функции
Упражнение №4
Отображение погрешностей
В уже использованном модуле numpy есть метод polyfit, позволяющий приближать данные методом наименьших квадратов. Он возвращает погрешности и коэффициенты полученного многочлена.
Упражнение №5
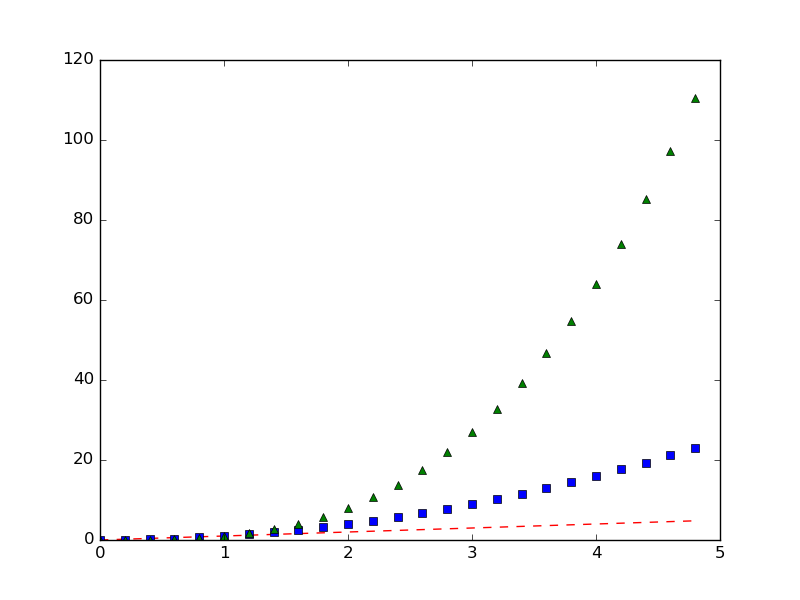
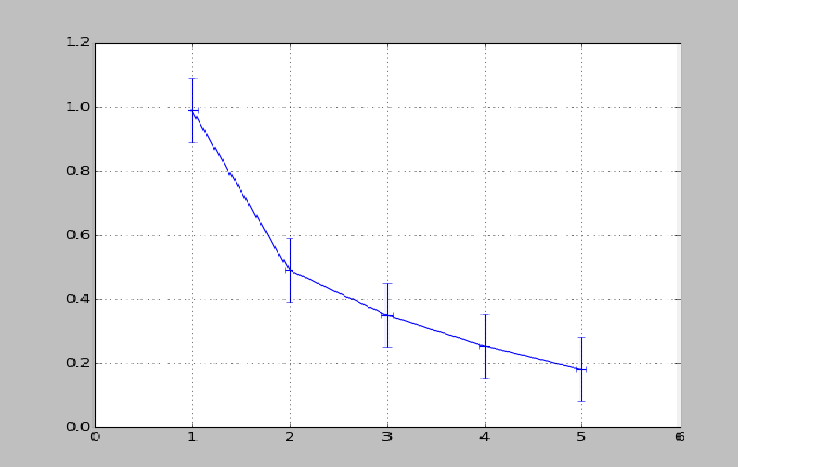
Приблизить данные из приведённого примера с погрешностями или свои собственные (из лабораторного практикума по общей физике) многочленами первой и второй степени. Начертить точки с погрешностями и полученные аппроксимационные кривые на одном графике.
Как нанести погрешности на графике в Excel
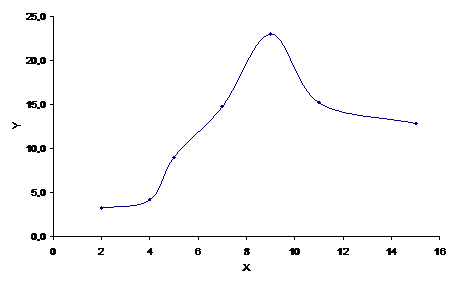
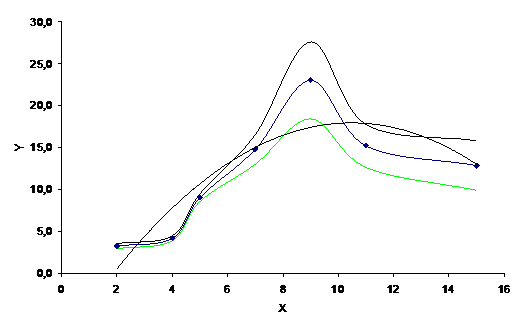
Как построить график в Excel с учетом погрешностей? Подобная задача нередко возникает у студента при обработке результатов лабораторных работ. Результаты представляют собой, как правило, два массива данных (в общем случае Х и Y). Пусть, для примера, имеется следующая экспериментальная зависимость:
| Х | 2,0 | 4,0 | 5,0 | 7,0 | 9,0 | 11,0 | 15,0 |
| У | 3,2 | 4,2 | 9,0 | 14,8 | 23,0 | 15,2 | 12,8 |
Требуется представить эту зависимость Y от Х графически. Получится примерно то, что представлено на рисунке.
Например, в ходе лабораторной работы студент измерял зависимость силы тока в одной из ветвей электрической цепи (в Амперах) от напряжения на том или ином ее элементе (в Вольтах). Необходимо отложить данные на графике с учетом погрешностей.
Вроде бы, все правильно. Да только график построен строго по точкам. Видно, что зависимость немонотонная, с достаточно острым максимумом – что не всегда имеет место в реальности. Ибо в реальности подавляющее большинство зависимостей могут быть более плавными.
Конечно, здесь надо смотреть, какие конкретно показатели анализируются. Если это, к примеру, динамика биржевого курса ценных бумаг; или – динамика поступления платежей от покупателей, равно как и другой аналогичный экономический показатель, то, конечно, можно с уверенностью сказать, что график вовсе не обязан быть плавным. В самом деле, очень многие экономические показатели меняются, как правило, скачкообразно.
Но, вроде бы, и здесь нет никаких проблем: следует провести линию тренда, которых Excel предлагает несколько типов. Так, можно выбрать линейный, степенной, экспоненциальный и т.д. тренд.
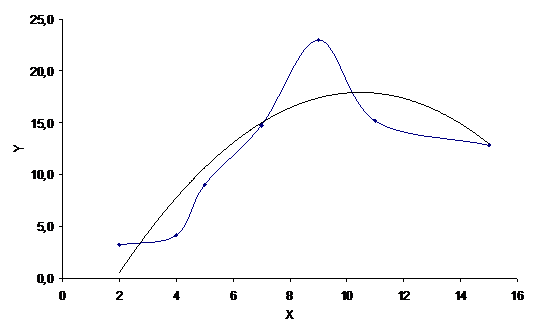
Можно… На примере выбранных нами данных, выбор показал, что наиболее близким для выбранной совокупности данных является параболический тренд. Отобразим его на рисунке.
Вроде бы, то, что проведено черной линией (тренд), уже гораздо ближе к истине. Правда, совсем ненамного. Фактически, проведенный тренд достаточно хорошо соответствует исходным данным только для 3, 4 и 7-й точек. Для остальных точек имеются существенные расхождения, причем ошибка доходит до 80%.
Ясно, что построенный тренд, в силу его высокой погрешности, в данном случае никак нельзя принять в качестве качественного графика, отражающего ход зависимости, выявленной экспериментально. Однако, и первоначально построенную (синюю) линию, вероятно, также нельзя принять в качестве такового, ибо, повторимся, она вообще не учитывает погрешностей.
Как же быть?
Однако, тогда, в любом случае, придется писать программу (в MatLab это будет проще, в Excel – посложнее, ибо там придется программировать вручную готовые функции, которые уже имеются в MatLab ). А для студента, которому требуется обработать данные лабораторной или (реже) контрольной работы, это может являться сложной, отдельной задачей. В самом деле, вместо анализа результатов он вынужден вначале думать, каким образом построить эти результаты, а потом программировать. Добро, если лабораторная работа проходит на старшем курсе. Однако, зачастую, студент делает их, начиная с самого начала своего обучения, т.е. когда опыта математической обработки, не говоря уже об умении строить интерполяционные многочлены, нет вообще.
Какими бывают погрешности
Погрешности бывают, в общем случае, относительные (в процентах) и абсолютные (выраженные в единицах измеряемой величины). Кроме того, они могут иметь постоянное значение или переменное.
Да, все вроде бы, замечательно. Но только график, приведенный на сайте (по указанной ссылке), также построен, строго говоря, неверно. Дело в том, следует повторить, что график должен представлять собой, по возможности, плавную линию. Которая где-то пройдет через середину интервала погрешности, а где-то, быть может, через один из его краев. Так вот, стандартные средства Excel даже самых новых версий не позволяют построить такой график автоматически. Тем более, если идет речь о том, что каждая экспериментальная точка может иметь, вообще говоря, разную погрешность.
Когда это бывает?
Например, в случае, когда разные экспериментальные точки были получены на базе исследований, проведенных разными методами.
Например, взять эксперименты по измерению зависимости внутреннего трения (т.е. степени перехода механической энергии в тепловую при упругих деформациях) материалов от частоты упругой деформации.
Таким образом, даже ориентировочное рассмотрение выявило, что существуют, как минимум, четыре основных диапазона частот, для каждого из которых может быть применен какой-либо свой метод исследования, кардинально отличающийся от других. Соответственно, у каждого из методов может быть свое значение погрешности (относительной или абсолютной).
Как построить плавный график в Excel с учетом погрешностей?
Рассмотрим самый сложный, общий случай – разных погрешностей для каждой из экспериментальных точек и покажем, как можно применить Excel для того, чтобы построить корректный график зависимости.
Пусть погрешности экспериментальных точек равны следующим значениям:
Ясно, что как относительная, так и абсолютная погрешности данных будут разными для каждой из экспериментальных точек. Однако, для каждой из них можно определить минимальное и максимальное значения (через интервал которых и должен пройти график). Проведем такой расчет (благо, при помощи Excel это сделать очень легко и быстро):
| Х | 2,0 | 4,0 | 5,0 | 7,0 | 9,0 | 11,0 | 15,0 |
| Y | 3,2 | 4,2 | 9,0 | 14,8 | 23,0 | 15,2 | 12,8 |
| Относительная погрешность (для Y), % | 10 | 7 | 5 | 12 | 20 | 17 | 23 |
| Минимальное значение Y | 2,9 | 3,9 | 8,6 | 13,0 | 18,4 | 12,6 | 9,9 |
| Максимальное значение Y | 3,5 | 4,5 | 9,5 | 16,5 | 27,6 | 17,8 | 15,8 |
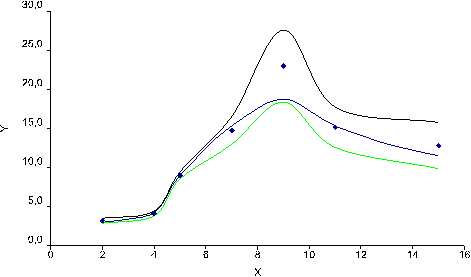
Минимальные и максимальные значения Y образуют допустимый интервал (диапазон), в котором может находиться график. Отложим этот диапазон на рисунке.
Нижняя граница диапазона показана зеленой линией, верхняя – черной. Толстая черная линия – это ранее нанесенные тренд. Четко видно, что тренд (даже, повторимся, оптимальный, выбранный из предлагаемого программой Excel перечня) только в двух (из семи) экспериментальных точках проходит в пределах допустимой области. Следовательно, необходимо отказаться от него. Удалим его с рисунка.
Итак, построена допустимая область. Искомый график зависимости должен лежать внутри нее, при этом имея, по возможности, наиболее плавный вид.
Его построение (если расчет оптимального интерполяционного многочлена вызывает сложность) проще провести вручную. Т.е. распечатать на бумаге полученный рисунок и уже на нем нанести график. Но, вполне возможно это сделать и при помощи компьютера – чтобы вообще не возиться с пишущими принадлежностями, причем сделать это можно очень быстро.
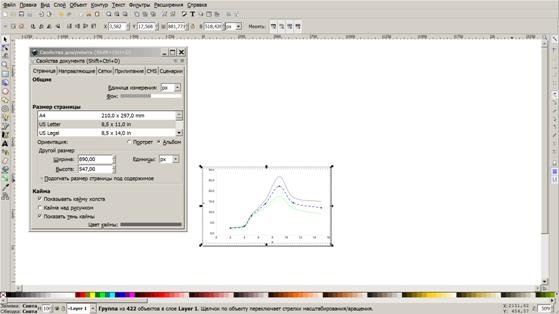
Для этого удобнее всего использовать программу Inkscape. Она является совершенно бесплатной, если у Вас она еще не установлена, можете скачать ее с официального сервера. https://inkscape.org/ru/download/
Устанавливаем ее, затем открываем. Копируем рисунок (отметим, лучше это сделать не из Word, а из первоисточника, т.е. из Excel).
Затем, как обычно, нажимаем кнопку «Вставить», размещаем рисунок примерно по центру рабочей области. Если ее размеры не совпадают с рисунком, нужно ее настроить, для чего нажимаем « Файл », « Свойства документа » и там устанавливаем альбомную ориентацию и указываем требуемые размеры (параметры «Ширина» и « Высота »). Примерно вот что должно получиться в итоге.
Так как Excel создает диаграммы в векторном виде, они без проблем редактируются в Incscape. Таким образом, наша задача – вручную таким образом исправить синюю линию, чтобы она стала как можно более плавной.
Затем нажимаем в меню пункт « Контур », « Упростить ». Число узлов значительно снизится, останутся лишь основные. Кстати, если кликнуть по каждому узлу в отдельности, его можно будет стереть путем нажатия клавиши « Delete ». Но, это будет достаточно долго, поэтому проще использовать команду » Упростить «.
Затем, удерживая левую кнопку мыши на соответствующем узле, двигаем его в ту или иную сторону. Так повторяем с другими узлами (при необходимости скорректировать кривизну линии в конкретном узле, можно также двигать рычаги каждого из них).
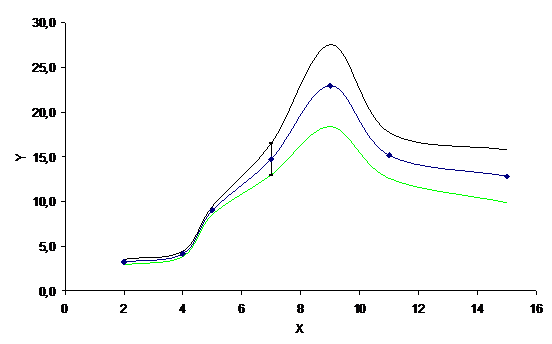
В итоге линия принимает вид, показанный на рисунке.
Для наглядности (чтобы можно было помнить, где проходила линия графика, построенная в Excel), экспериментальные точки, в виде синих ромбиков, оставлены.
Таким образом, мы получили сглаженный, более плавный график, чем тот, который был построен автоматически в Excel. Даже не взяв в руки карандаш или иной пишущий инструмент: использовались лишь некоторые клавиши и мышь.
Наносим линии погрешностей
Так что, в данном случае, можно начертить их вручную (т.е. нарисовать мышкой соответствующие вертикальные линии, проходящие через каждую экспериментальную точку).
Однако, это, на наш взгляд, утомительно. Поэтому, если совсем не хочется возиться с ручным рисованием, выход вполне есть – их можно выполнить, нарисовав соответствующее (в данном случае 7) дополнительных графиков. Повторимся, это следует сделать ДО того, как преобразовывать диаграмму в Inkscape.
Итак, заходим на вкладку « Диаграмма ». Нажимаем в панели инструментов « Диаграмма », « Исходные данные ». Выбираем вкладку « Ряд », затем нажимаем «Добавить».
Теперь выбираем значения Y. После нажатия красной стрелочки, перейдя на нужный Лист, кликаем на минимальное значения Y, соответствующее Х, равному 7. Затем, удерживая клавишу « Ctrl », кликаем максимальное значение Y. В итоге, через точку с запятой в адресной строке должны появиться адреса двух ячеек, соответствующие минимальному и максимальному значению Y (для Х=7).
Его можно потом перенести в Inkscape и придать графику (синяя линия) более плавный вид.
Exceltip
Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки
Планки погрешностей в Excel — нестандартное использование
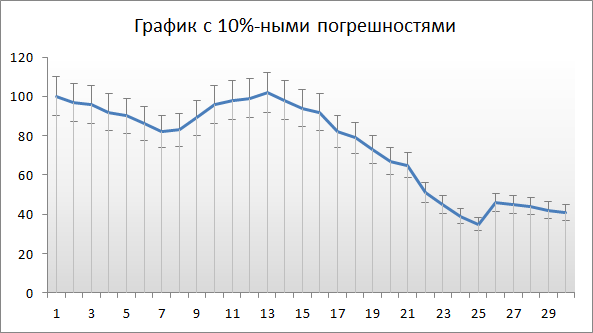
Ряды данных диаграмм могут включать планки погрешностей, которые предоставляют дополнительную информацию о данных. К примеру, вы можете использовать планки погрешностей для отображения количества ошибок или неопределенностей для каждой точки ряда данных.
На рисунке отображен график Excel с планками погрешностей, которые указывают на диапазон ошибок для каждой точки. В данном случае погрешность основана на процентах – плюс/минус 10 процентов. Планка для первой точки ряда данных (значение 100) находится в пределах от 90 до 110.
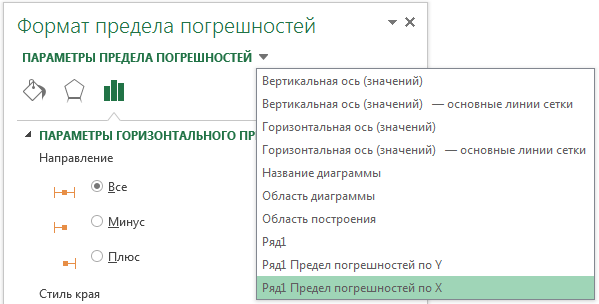
Добавление планки погрешности к ряду данных
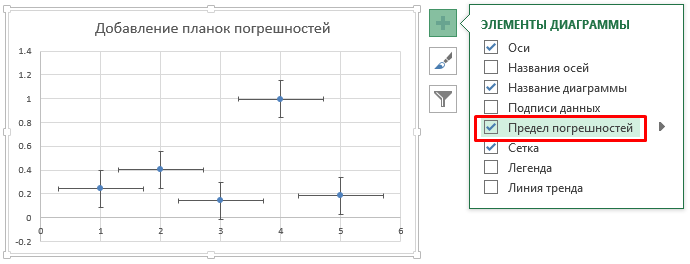
Если у вас точечная или пузырьковая диаграмма, вы можете определять значения планок погрешностей как для вертикальных, так и для горизонтальных пределов. Чтобы переключиться между ними, необходимо в диалоговом окне Формат предела погрешностей щелкнуть по треугольнику рядом с полем Параметры предела погрешностей и выбрать соответствующий.
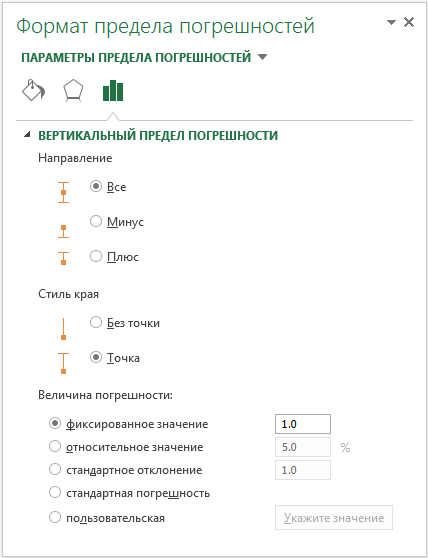
Сперва необходимо определиться с направлением планок погрешностей: выше, ниже или в обе стороны от точки ряда данных. Для горизонтальных пределов погрешностей доступны те же опции, только в горизонтальном направлении. Далее определяемся со стилем края, будет ли она ограничиваться чертой на конце планки, либо нет. И выбираем одну из пяти вариантов величины погрешности:
Фиксированное значение: Планка погрешности будет смещена на, указанную вами, фиксированную величину от точки ряда данных. Каждая планка будет одинаковой высоты (или ширины для горизонтальных планок).
Относительное значение: Планка погрешности будет смещена от точки ряда данных на заданных процент от значения точки. К примеру, если вы задали относительное значение равным 5%, а точка ряда данных равна 100, предел погрешности будет находиться в диапазоне от 95 до 105. Т.е. в зависимости от значения точки ряда данных, предел погрешности будет различаться.
Стандартное отклонение: Планки погрешностей будут центрированы по невидимой линии, которая представляет среднее значение ряда данных, выше или ниже на то значение, которое было указано в поле. Для этой опции величина планки погрешностей не зависит от значения точки ряда данных и всегда параллельна оси.
Стандартная погрешность: Размер планки погрешности задается в единицах среднеквадратичной ошибки, которую Excel вычисляет для ряда данных.
Пользовательская: Планки погрешностей определяются значениями диапазона данных, который вы указали. Обычно они содержат формулы.
В Excel 2013 пределы погрешностей можно добавить еще одним способом. Выберите ряд данных и щелкните по иконке справа от диаграммы в виде плюсика. В появившемся справа, выпадающем меню Элементы диаграммы, поставьте галочку напротив поля Предел погрешностей. При необходимости можете задать уточняющие параметры, нажав по стрелке рядом с полем.
Нестандартное использование планок погрешностей в Excel
На самом деле, за все свое знакомство с Excel, я ни разу не воспользовался планками погрешностей по их прямому назначению. Более того, ни разу не встречал людей, которые бы ими пользовались. Если уж дальше развивать эту тему, скажу, что их используют как угодно, но только не так, как задумывалось изначально.
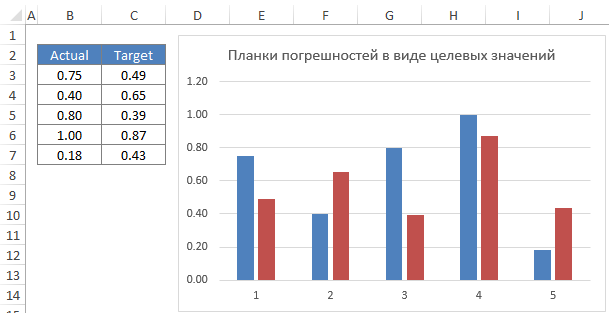
Наиболее распространенный способ использования планок погрешностей в Excel – в виде целевых значений. К примеру, у вас есть пять KPI (показателей эффективности) со своими целевыми значениями и вы хотите отобразить текущее и целевое значение на одном графике. Строим гистограмму с двумя рядами данных.
Меняем тип диаграммы для целевого ряда данных на точечный, чтобы была возможность строить горизонтальные планки погрешностей. Для этого щелкаем правой кнопкой по целевому ряду данных, из выпадающего меню выбираем Изменить тип диаграммы для ряда. В появившемся диалоговом окне, меняем тип диаграммы на точечный. Далее к нему добавляем планки погрешностей, любым из описанных выше способов. Удаляем вертикальные пределы. Форматируем планку и точку ряда данных по нашему усмотрению. Получаем диаграмму с пятью фактическими и целевыми значениями.
Данный подход применялся в одной из предыдущих статей, когда мы с вами распределяли показатели на дашборде.
Вам также могут быть интересны следующие статьи
6 комментариев
Добрый день!Подскажите,пож-та,как можно построить диаграмму с использованием планки погрешностей,для данных в прикрепленном файле?На Ваш сайт забрела случайно,нахожу его интересным!
Не совсем понял, для каких данных, вы хотите построить планку погрешностей. Пришлите, пожалуйста, файл с диаграммой, куда вам необходимо добавить планки погрешностей, там посмотрим
Здравствуйте.
Мне требуется вычислить и добавить к графику данные, вычисленные по следующим формулам (на фото, вставлен в excel — иначе не прикрепляется).
Насколько я понимаю, стандартная погрешность в статье совпадает с функцией среднеквадратичной ошибки, которая вычисляется по формуле среднего квадратичного отклонения.
Есть ли стандартные действия для вычисления средней квадратичной ошибки из фото?
Буду благодарна за Ваш ответ.
Подскажите, пожалуйста, как добавить погрешность для каждого значения, если для графика я беру среднее.
Например, мoи числа 5, 6, 7. Среднее 6, но я хотела бы показать на графике индивидуальную погрешность, то есть не +/- 5%, а именно, что это среднее между тремя числами.
Нужно вбить значение погрешностей строкой в соотвествии за значениями средних. И когда будете задавать значения погрешностей через «пользовательское», выбрать весь рядзначений погрешностей. Тогда эксель расставит таким образом, что каждая линейка погрешностей будет соответствовать среднему
Записки дебианщика
В этом блоге публикуются заметки и решения, найденные в процессе работы, освоения и жизни в дистрибутиве Debian GNU/Linux.
Как построить графики с погрешностями в gnuplot по экспериментальным данным
В этом случае, чтобы построить график с погрешностями по оси Y, например, последняя команда в скрипте для графика будет выглядеть так:
Общая идея, думаю, понятна: сначала указываются колонки, содержащие данные, а потом колонки, содержащие значения погрешностей. Таблица, любезно утянутая отсюда, даёт прекрасную иллюстрацию:
| Data Format | Column | using | with |
|---|---|---|---|
| (X,Y) data | X Y | 1:2 | lines, points, steps, linespoints, boxes, etc. |
| Y has an error of dY | X Y dY | 1:2:3 | yerrorbars |
| X has an error of dX | X Y dX | 1:2:3 | xerrorbars |
| Y has an error of dY, and X has an error of dX | X Y dX dY | 1:2:3:4 | xyerrorbars |
| Y has a range of [Y1,Y2] | X Y Y1 Y2 | 1:2:3:4 | yerrorbars |
| X has a range of [X1,X2] | X Y X1 X2 | 1:2:3:4 | xerrorbars |
| Y has a range of [Y1,Y2], and X has a range of [X1,X2] | X Y X1 X2 Y1 Y2 | 1:2:3:4:5:6 | xyerrorbars |
Для иллюстрации разберу два рабочих примера с построением графиков с погрешностями и аппроксимацией данных.
16 18 0.72 10 whiteLEDS 1 10
12 30 0.61 12 greenUltraBrightLEDS 1 10
8 200 0.45 20 HGlamp 1 15
6 1600 0.35 35 AlGaAsLser 1 50
4 17000 0.28 68 NdYAG-laser 1 900
4 25000 0.27 70 HeNeLaser 1 1100
Нужно построить зависимость первой колонки от второй, при этом погрешности по оси X составляют 7% от данных, а по оси Y указаны в колонке 7. Вот такой при этом получается код для gnuplot:
Результат строительства графика: 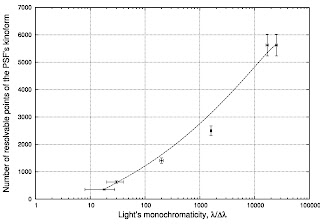
Ну и наконец нужно было построить квадратичную зависимость по оси Y, что реализовано так: ((300/$1)**2) т о есть число 300 делится для каждой точки на значение в первой колонке, результат возводится в квадрат.
Пример 2. Построить график с погрешностями и аппроксимацией в gnuplot
Задачка посложнее: здесь требовалось экспериментальные точки аппроксимировать прямой линией и погрешностями. Из части данных нужно вычесть постоянную составляющую, так что работы для gnuplot хватает. Итак, сеанс чёрной магии с полным её разоблачением:
Здесь я отмечу то, что сам часто забываю: директиву every можно использовать не только при подгонке, но и для других графиков. Для этого полезно иметь перед глазами таблицу, которую изваял автор not so Frequently Asked Questions:
Теперь осталось построить два графика на одном:
plot «./RAWMEANmeasurementresult» using 4:($3-255.22579):7 title «Digital values of photosensor signal» with yerrorbars linestyle 1, f(x) title «linear fitting function» with line
То есть строим зависимость колонки 3 от 4 и используем колонку 7 как источник погрешности. При этом накладываем аппроксимационную линию с помощью директивы f(x) title «linear fitting function» with line
Собственно, вот итог моих фокусов: 
Красиво и вполне себе презентабельно, хоть в Nature отправляй.