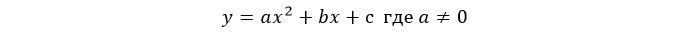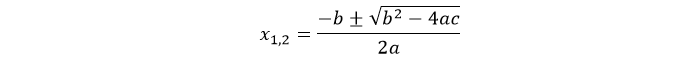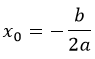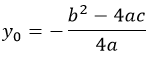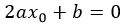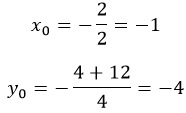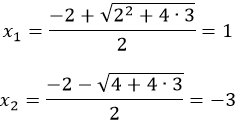Как построить график по дискриминанту
Определение и формула квадратичной функции
Квадратичной называют функцию канонического вида:
Формально конструкция именуется «квадратный трехчлен». Сразу заметно, что область определения не ограничена, а четность не выявлена.
Примеры построения парабол
Займемся упрощенными случаями и подметим закономерности.
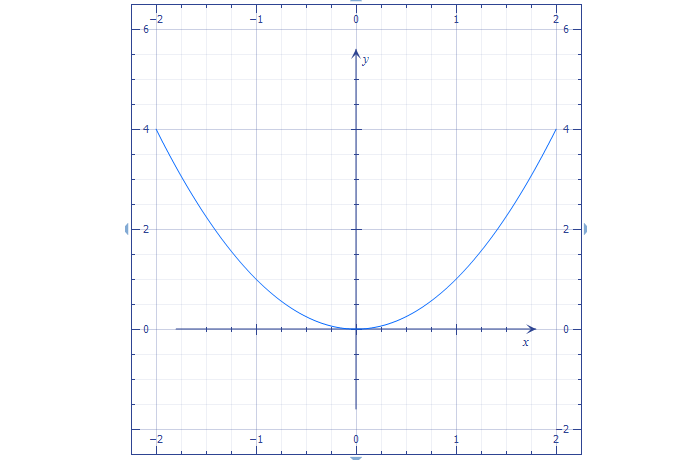
График функции при а = 1, b = c = 0
Наиболее тривиальная, но наглядная и информативная разновидность с формулой:
Функция четная, возрастающая. Построим по точкам.
Получившаяся кривая называется «парабола». Характерна для уравнений с «квадратом».
Нижнюю точку с координатами (0; 0) называют «вершиной». Единственное место, где одной функции соответствует один аргумент. В данном случае – это минимум функции.
Уходящие вверх части кривой – «ветви». На всех участках кроме вершины к одному (y) относятся сразу (±x).
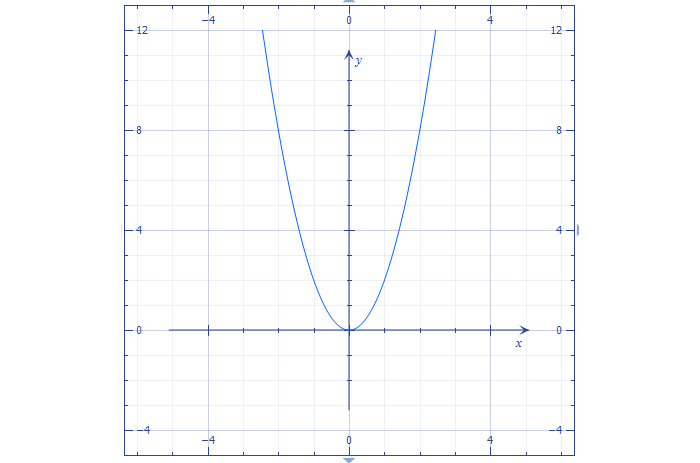
График функции, когда b = c = 0, а > 1 и а y = 2x 2
Ветви «сожмутся» относительно оси симметрии.
Построим другой график.
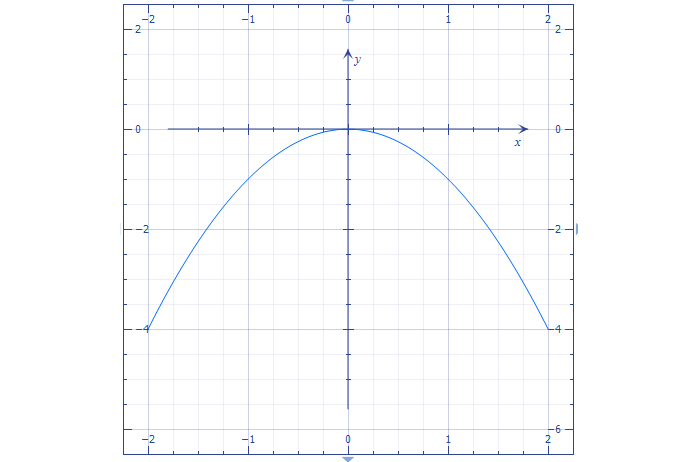
Куда интереснее переместить коэффициент a в отрицательную область.
Парабола «повернется» на 180°. И вершина станет максимумом.
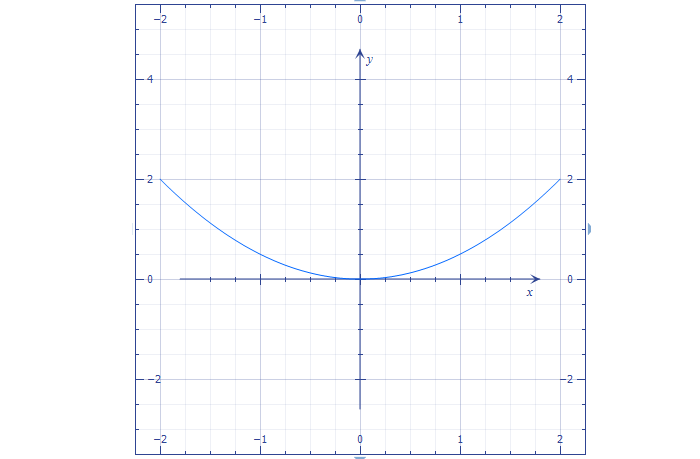
График функции при b = 0, с ≠0
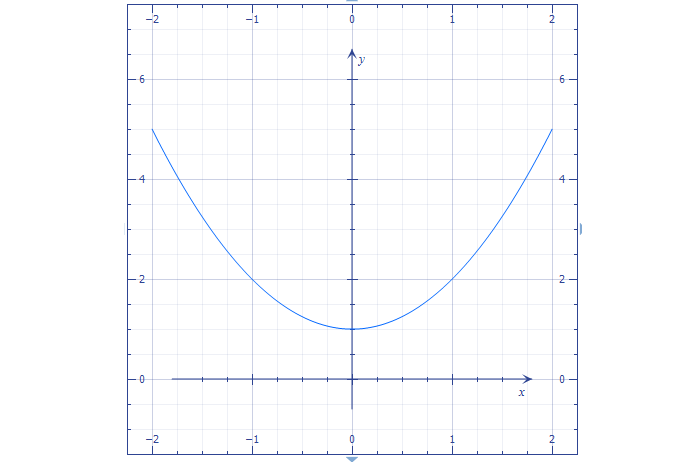
Рассмотрим такой вариант:
Вершина сдвинется на величину c по оси Y.
А если параметр c отрицателен? Уравнение выглядит так:
Смещение произойдет ниже точки (0; 0).
Общий случай a ≠0, b ≠0, c ≠0
Попробуем найти характерные точки.
Пересечения с осью абсцисс (y = 0)
Иными словами, следует решить уравнение:
Корнями уравнения будут:
Подкоренное выражение называется «дискриминант» и обозначается «D». Появляются варианты:
D отрицателен, D > 0. В таком случае действительные корни не существуют. Парабола не пересекает ось Х.
D положителен, D > 0. Существуют оба корня. Кривая пересекает X в двух известных местах.
D = 0. Корень один – -b/2a. Пересечение единственно. А такое возможно в одном случае: найденное означает абсциссу вершины.
Вершина
Горизонтальная координата вычисляется по формуле:
Касательная в вершине параболы совпадает с осью X или параллельна ей. Значит тангенс её относительного наклона равен 0. А это производная функции:
Нашли x0, а y0 находится подстановкой в уравнение найденного.
Ось симметрии
Параллельная оси ординат прямая x = x0.
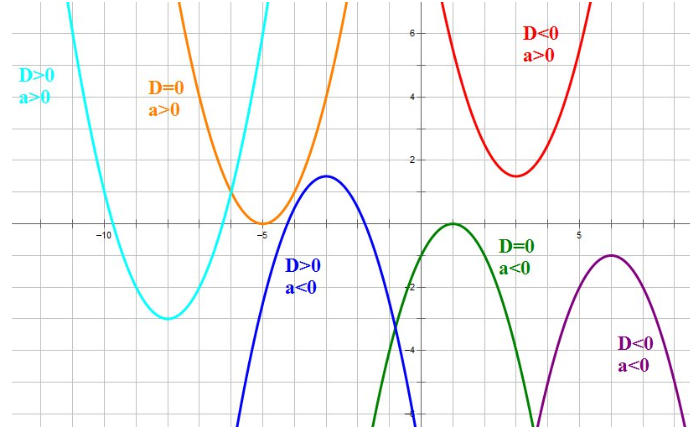
Приблизительный вид
По уравнению можно прикинуть общую картину:
положительное значение коэффициента a говорит о направленности ветвей вверх и наоборот;
по дискриминанту определим расположение относительно X;
находим пересечения (если есть).
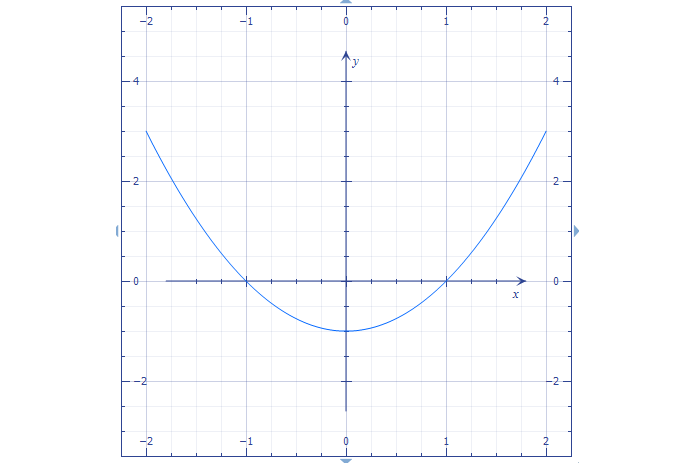
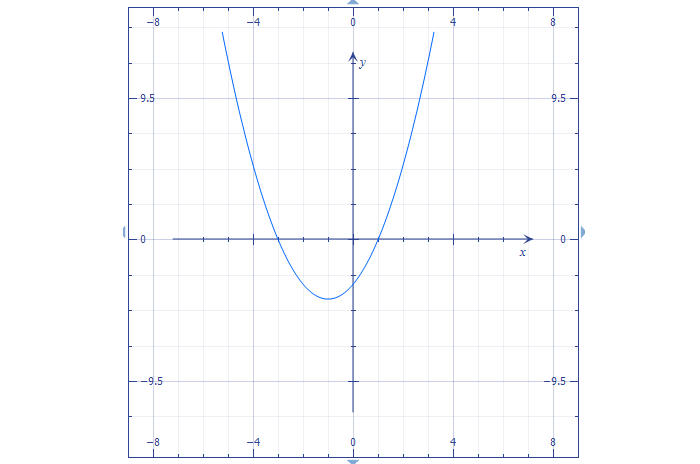
Пример построения графика
a = 1, положительный, поэтому ветви параболы направлены вверх;
Алгоритм построения графика квадратичной функции:
2. Определяем точки пересечения с осью X:
Свойства параболы
Основные свойства следующие:
Область определения – все действительные числа.
Координаты вершины зависят только от коэффициентов.
Ось симметрии проходит через вершину и параллельна оси ординат.
Заключение
В интернете существует масса онлайн-калькуляторов для облегчения работы с кривой. Приведенные же приемы и перечисленные свойства позволяют лучше понять сущность квадратичного выражения.
Параболические отражатели позволяют получать параллельный пучок света от точечного источника. Антенна такого типа позволяет концентрировать и усиливать радиосигнал. Не абстрактная линия на бумаге.
Как построить график по дискриминанту
§4. Построение графиков функций
При помощи построения графика квадратичной функции можно решать квадратные неравенства.
б) `4x^2+4x+1 0` и `c 0` и данное уравнение имеет корни.
Определите знаки коэффициентов квадратного трёхчлена `y=ax^2+bx+c`, график которого изображён на рис. 12.
1) Заметим, что `y(0)=c`, откуда `c>0`.
2) Ветви параболы направлены вниз `=>a 0`, откуда `b>0`.
Найти все значения `l`, при которых неравенство
`lx^2-2(l-6)x+3(l-2) (если `b 0`).
3) График сдвигается на `|c|` вверх при `c>0` и на `|c|` вниз при `c
г) Отметим на числовой прямой точки, в которых выражения, стоящие под знаком модуля, обращаются в ноль (рис. 16а). Эти три точки делят числовую прямую на четыре части, причём на каждой из частей знаки выражений, стоящих под модулями, не меняются.
1) `ul(x 0`, `x-3 0`, `x-3 0`, поэтому
Получаем отрезок (часть прямой `y=8`, заключённая между прямыми `x=-1` и `x=3`).
4) `ul(x>3)`. Тогда `x+4>0`, `x-3>0`, `x+1>0`, поэтому
Получаем луч (часть прямой `y=2x+2`, находящуюся справа от прямой `x=3`). График см. на рис. 16б.
Укажем второй способ построения. На каждом из четырёх участков `(-oo;-4]`, `[-4;-1]`, `[-1;3]`, `[3;+oo)` после раскрытия модулей получим линейную функцию, графиком которой является прямая. Чтобы построить прямую, достаточно знать две её точки. Отсюда вытекает следующий способ построения. Вычислим значения функции в точках `x=-4`, `x=-1` и `x=3`, а также в каких-либо точках, лежащих на промежутках `(-oo;-4)` и `(3;+oo)`, например, `x=-5` и `x=4`. Получаем пять точек, принадлежащих графику:
Проводим отрезки `AB` и `BC`, лучи `AD` и `CE` и получаем график.
д) Построим сначала график функции `f_1(x)=|x|-3` (рис. 17а).
График `f_2(x)=||x|-3|` получается из графика функции `f_1(x)` так: точки, лежащие выше оси `Ox` и на оси `Ox` сохраняются, а все точки, лежащие ниже оси `Ox`, отражаются относительно оси `Ox` в верхнюю полуплоскость (рис. 17б). Действительно, если `f_1(x)>=0`, то `f_2(x)=|f_1(x)|=f_1(x)`, а если `f_1(x) =0`, то точки на графике для `f_1(x)` и `f_2(x)` совпадают. Если же `f_1(x) =0` этот график совпадает с графиком функции `f(x)=x^2-4x+3`.
Отсюда вытекает следующий способ построения. От графика функции `y=x^2-4x+3` оставим точки, лежащие справа от оси `Oy`, отразим их симметрично относительно этой оси, а точки, лежащие слева от оси `Oy`, отбросим (рис. 18в).
График функции `y=f(|x|)` получается из графика функции `y=f(x)` следующим образом. Отбрасываем все точки, лежащие слева от оси `Oy`, а оставшиеся точки отражаем относительно оси `Oy`.
г) Есть 2 способа построения.
(1) Все точки графика из пункта (в), лежащие ниже оси абсцисс, отражаем относительно этой оси.
(2) От графика пункта (б) отбрасываем точки, лежащие слева от оси ординат; все точки, находящиеся справа от оси ординат, отражаем относительно неё. Разумеется, в обоих случаях получается одинаковый результат (рис. 18г).
Теперь рассмотрим график функции `y=(ax+b)/(cx+d)`; при этом считаем, что
2) коэффициенты в числителе и в знаменателе не пропорциональны друг другу, т. е. `ad!=bc`. (Если `ad=bc`, то `b=(ad)/c` и получаем
Покажем на примере, как этот график может быть построен.
Постройте график функции:
б) Отношение коэффициентов при `x` в числителе и знаменателе дроби равно `(-3/2)`.
Преобразуем данную дробь, добавляя и вычитая `(-3/2)`:
Дроби в скобках приводим к общему знаменателю:
`y=-3/2+(12-6x+6x+3)/(2(2x+1)) iff y=-3/2+15/(4x+2) iff`
Этот график получается из графика `y=(15//4)/x` параллельным переносом на `3/2` вниз и на `1/2` влево (рис. 20).
Квадратичная функция (парабола)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
После этого по точкам строили график: 
Параболу y = ax 2 + bx + c мы не станем строить каждый раз «по точкам» — для выпускника школы это просто несолидно. Ведь нам надо знать закономерности поведения данной функции. А эти закономерности таковы.
1. Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a 2 с равными по модулю, но противоположными по знаку значениями a.

2. Абсолютная величина коэффициента a отвечает за «раскрыв» параболы. Чем больше |a|, тем у́же парабола (больше прижата к оси Y ). Наоборот, чем меньше |a|, тем шире парабола (больше прижата к оси X).

3. Абсцисса вершины параболы y = ax 2 + bx + c находится по формуле:
Для нахождения ординаты вершины y0 удобнее всего подставить x0 в уравнение параболы. Но вообще, полезно помнить, что
где D = b 2 − 4ac — дискриминант.
4. Точки пересечения параболы y = ax 2 + bx + c с осью X находятся с помощью решения квадратного уравнения ax 2 + bx + c = 0. Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X.
5. Точка пересечения с осью Y находится легко: мы просто подставляем x = 0 в уравнение параболы. Получается точка (0, c).
А теперь покажем, как с помощью графика функции y = ax 2 + bx + c решать квадратные неравенства.
1. Часто на тестировании мы предлагаем решить неравенство
x 2 2 и отметим все значения x, для которых y 2 − 3x − 10 ≥ 0.
Графиком функции y = x 2 − 3x − 10 служит парабола, ветви которой направлены вверх. Решая квадратное уравнение x 2 − 3x − 10 = 0, находим x1 = −2 и x2 = 5 — в этих точках парабола пересекает ось X. Нарисуем схематично нашу параболу:

Мы видим, что при x ∈ (−2; 5) значения функции отрицательны (график проходит ниже оси X). В точках −2 и 5 функция обращается в нуль, а при x 5 значения функции положительны. Следовательно, наше неравенство выполняется при .
Обратите внимание, что для решения неравенства нам достаточно было схематично изобразить параболу. Ось Y вообще не понадобилась!
3. Ещё одно неравенство: x 2 + 2x + 4 > 0.
Ветви параболы y = x 2 + 2x + 4 направлены вверх. Дискриминант отрицателен, т. е. уравнение x 2 + 2x + 4 = 0 не имеет корней. Стало быть, нет и точек пересечения параболы с осью X.
Раз ветви параболы направлены вверх и она не пересекает ось X — значит, парабола расположена над осью X.

Получается, что значения функции положительны при всех возможных x. Иными словами, решения нашего неравенства — это все действительные числа.
Ответ: .
Квадратные неравенства являются неотъемлемой частью ЕГЭ. Разберём типичные примеры из банка заданий ЕГЭ.
4. Завиcимоcть объeма cпроcа q (тыc. руб.) на продукцию предприятия-монополиcта от цены p (тыc. руб.) задаeтcя формулой q = 100 − 10p. Выручка предприятия за меcяц r (в тыc. руб.) вычиcляетcя по формуле r(p) = q · p. Определите наибольшую цену p, при которой меcячная выручка r(p) cоcтавит не менее 240 тыc. руб. Ответ приведите в тыc. руб.
Подставим выражение для q в формулу выручки:
r(p) = qp = (100 − 10p)p = 100p − 10p 2
Выручка должна быть не менее (то есть больше или равна) 240 тысяч рублей. Поскольку цена p уже выражена в тысячах рублей, мы можем записать это условие в виде неравенства:
Переносим всё вправо и делим на 10:
Для схематичного построения параболы находим корни уравнения p 2 − 10p + 24 = 0. Они равны 4 и 6. Остаётся сделать рисунок. 
Решением нашего неравенства служит отрезок [4; 6]. Нас просили найти наибольшее p. Оно равно 6.
Итак, требуется, чтобы выполнялось неравенство h(t) ≥ 3. Подставляем сюда выражение для h:
Собираем всё справа:
Корни соответствующего уравнения 5t 2 −8t+1,4 = 0 равны t1 = 0,2 и t2 = 1,4. Как дальше действовать — мы знаем.

Таким образом, через t1 = 0,2 секунды после начала полёта мяч оказался на высоте 3 метра. Мяч продолжал лететь вверх, высота увеличивалась; затем началось снижение, высота уменьшалась, и в момент времени t = 1,4 секунды снова стала равна трём метрам над землей.
Получается, что мяч находился на высоте не менее трёх метров в течение t2 − t1 = 1,2 секунд. В бланк ответов вписываем десятичную дробь 1,2.
Согласно условию, зависимость температуры нагревательного элемента от времени определяется формулой:
T(t) = 1400 + 200t − 10t 2
В нормальном режиме работы прибора должно выполняться неравенство T ≤ 1760, или
1400 + 200t − 10t 2 ≤ 1760
Переносим всё вправо и делим на 10:
Находим t1 = 2, t2 = 18 и делаем рисунок: 
Получаем решения нашего неравенства:
Остаётся понять: в какой же момент отключать прибор? Для этого надо представить физическую картину процесса.
Мы включаем прибор в момент времени t = 0. Температура нагревателя повышается и при t = 2 мин достигает 1760 К. Затем повышение температуры продолжается, в результате чего прибор может испортиться. Поэтому ясно, что отключать его надо при t = 2.
Квадратичная функция.
Обратите внимание: коэффициент a может быть любым действительным числом, кроме нуля. Действительно, если a = 0, то ax 2 + bx + c = 0·x 2 + bx + c = 0 + bx + c = bx + c. В этом случае в выражении не остаётся квадрата, поэтому его нельзя считать квадратным трёхчленом. Однако, такие выражения-двучлены как, например, 3x 2 − 2x или x 2 + 5 можно рассматривать как квадратные трёхчлены, если дополнить их недостающими одночленами с нулевыми коэффициентами: 3x 2 − 2x = 3x 2 − 2x + 0 и x 2 + 5 = x 2 + 0x + 5.
Если стоит задача, определить значения переменной х, при которых квадратный трёхчлен принимает нулевые значения, т.е. ax 2 + bx + c = 0, то имеем квадратное уравнение.
Если существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax 2 + bx + c = a(x − x1)(x − x2)
Замечание: Если квадратный трёхчлен рассматривать на множестве комплексных чисел С, которое, возможно, вы еще не изучали, то на линейные множители его можно разложить всегда.
Когда стоит другая задача, определить все значения, которые может принимать результат вычисления квадратного трёхчлена при различных значениях переменной х, т.е. определить y из выражения y = ax 2 + bx + c, то имеем дело с квадратичной функцией.
При этом корни квадратного уравнения являются нулями квадратичной функции.
Квадратный трёхчлен также можно представить в виде
Это представление удобно использовать при построении графика и изучении свойств квадратичной функции действительного переменного.

Графиком квадратичной функции является парабола, вершина которой находится в точке 
Парабола обладает еще одним интересным свойством, которое также используется как её определение.
Парабола представляет собой множество точек плоскости, расстояние от которых до определенной точки плоскости, называемой фокусом параболы, равно расстоянию до определенной прямой, называемой директрисой параболы.
Построить эскиз графика квадратичной функции можно по характерным точкам.
Например, для функции y = x 2 берем точки
| x | 0 | 1 | 2 | 3 |
| y | 0 | 1 | 4 | 9 |
Соединяя их от руки, строим правую половинку параболы. Левую получаем симметричным отраженим относительно оси ординат.
Для построения эскиза графика квадратичной функции общего вида в качестве характерных точек удобно брать координаты её вершины, нули функции (корни уравнения), если они есть, точку пересечения с осью ординат (при x = 0, y = c) и симметричную ей относительно оси параболы точку (−b/a; c).
| x | −b/2a | x1 | x2 | 0 | −b/a |
| y | −(b 2 − 4ac)/4a | 0 | 0 | с | с |
| при D ≥ 0 | |||||
Производная квадратичной функции вычисляется по формуле (ax 2 + bx + c)’ = 2ax + b.
Формулы для такого перехода можно выучить наизусть, а можно научиться выделять полный квадрат из трёхчлена с заданными коэффициентами. Это умение весьма полезно также для решения некоторых уравнений и неравенств, для вычисления интегралов и т.д.
Итак, чтобы построить график функции y = 3x 2 − 5x + 2 из графика y = x 2 нужно последний сдвинуть по оси Ox вправо на 5/6 ≈ 0,83 единицы. Затем растянуть вдоль оси Oy в 3 раза и, наконец, опустить по оси Oy на 1/12 ≈ 0,08 единицы.
Посмотрите, что получилось.
Если Вы являетесь моим учеником или подписчиком, то можете поработать с интерактивными версиями этих графиков.
Преобразуем выражение с выделением полного квадрата: 
Строим график функции 
Видеоуроки с параболой.
Графики квадратичной функции и коэффициенты квадратного трёхчлена.
Положение и вид параболы в зависимости от знака и значения параметра c.
Построение параболы по характерным точкам.
Быстрое построение параболы как графика квадратичной функции.
Другие случаи. Примеры построения.
Задачи на анализ графика квадратичной функции.
Задания вида «Установить соответствие между коэффициентами квадратного трёхчлена и приведенными графиками квадратичной функции» встречаются в ОГЭ по математике в 9-ом классе, а также необходимы сдающим ЕГЭ за 11 класс в качестве промежуточного действия.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.