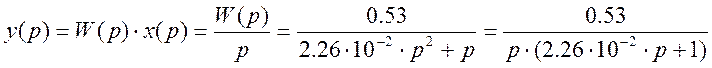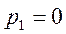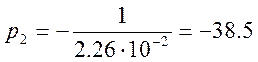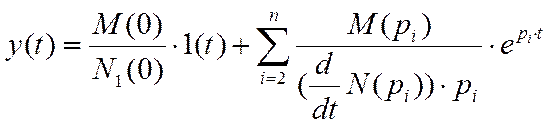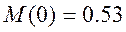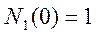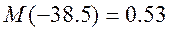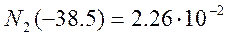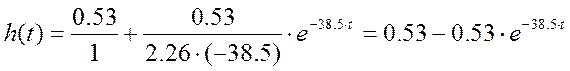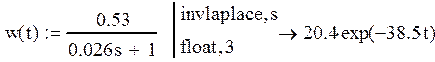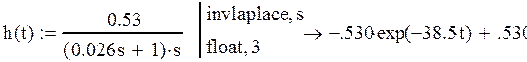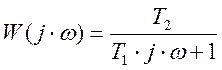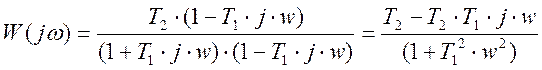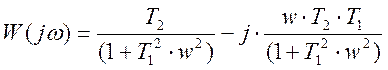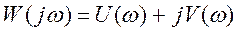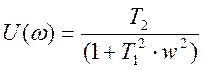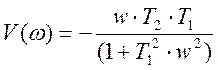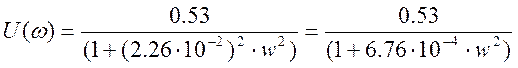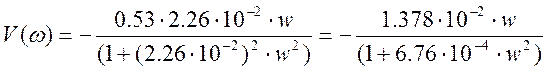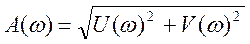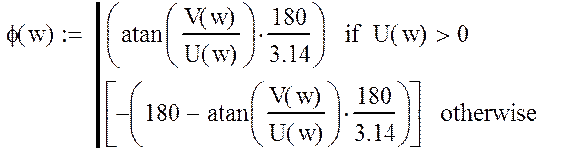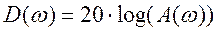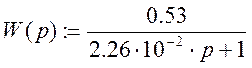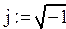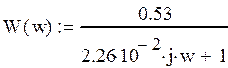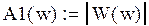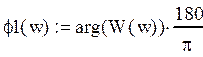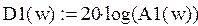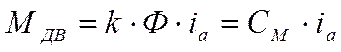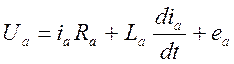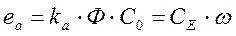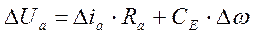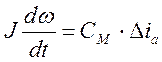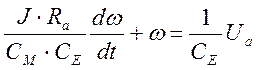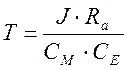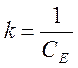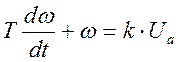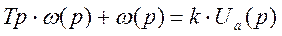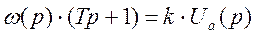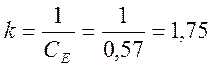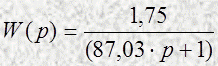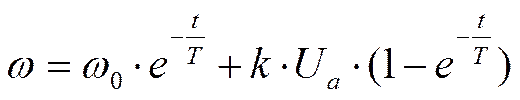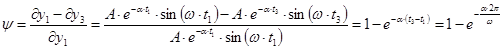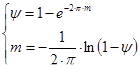Как построить график переходного процесса
Моделирование переходных процессов при коммутации электрической цепи средствами Python
Зачем нужно учитывать переходные процессы
В общем случае в электрической цепи переходные процессы могут возникать, если в цепи имеются индуктивные и емкостные элементы, обладающие способностью накапливать или отдавать энергию магнитного или электрического поля. В момент коммутации, когда начинается переходный процесс, происходит перераспределение энергии между индуктивными, емкостными элементами цепи и внешними источниками энергии, если они подключенными к цепи. При этом могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые способны нарушить работу систем автоматики и других устройств, вплоть до выхода их из строя.
С другой стороны, переходные процессы находят практическое применение, например, в различные рода электронных генераторах, в схемах электроники и автоматики.
В сети много публикаций по данной теме [1,2,3], однако большая их часть содержит описания переходных процессов, основанное на методах аналитического решения соответствующих уравнений. Численные методы используются значительно реже, причём большая часть таких публикаций посвящена описанию метода численного решения дифференциального уравнения.
Учитывая хорошо развитые в библиотеке SciPy численные методы, привожу пример математического моделирования переходных процессов при коммутации в электрических цепях средствами данной библиотеки.
Как можно построить графики переходных процессов при коммутации электрических цепей
Обобщённая схема электрической цепи.
Рассмотрим цепь, содержащую источник тока — E, катушку индуктивности – L, два сопротивления — R1, R2, конденсатор — C и рубильник.
Приведём параметры электрической цепи для состояния после коммутации.
В разомкнутом состоянии приведённая на рисунке цепь соответствует условиям:
Результат работы программы
В разомкнутой цепи i2=0, а i3=i1, поэтому на графике приведены только ток и напряжение. Характер переходных процессов – затухающие колебания.
В замкнутом состоянии приведённая на рисунке цепь соответствует условиям:
Результат работы программы
В замкнутой цепи для токов выполняется соотношение i1=i2+i3. Переходные процессы апериодические. В установившимся режиме i3=0, i1=i2, что и следует из графика.
Вывод
Численные решения дифференциальных уравнений средствами Python упрощают анализ переходных процессов в электрических цепях, делают его наглядным и позволяют сосредоточится на результатах без анализа методов решения уравнений.
Найдем обратное преобразование Лапласа от y(p). Для этого необходимо найти корни характеристического уравнения.
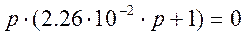
Т. к. корни простые (не комплексные), не кратные, и имеется один нулевой корень, то выражение для y(t) при t≥0 имеет вид:
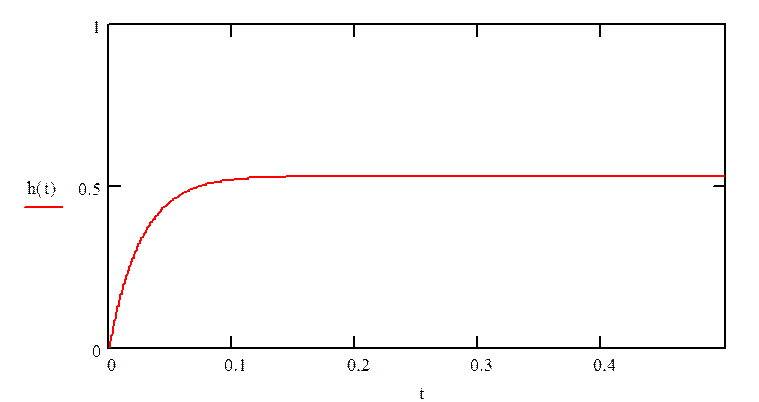
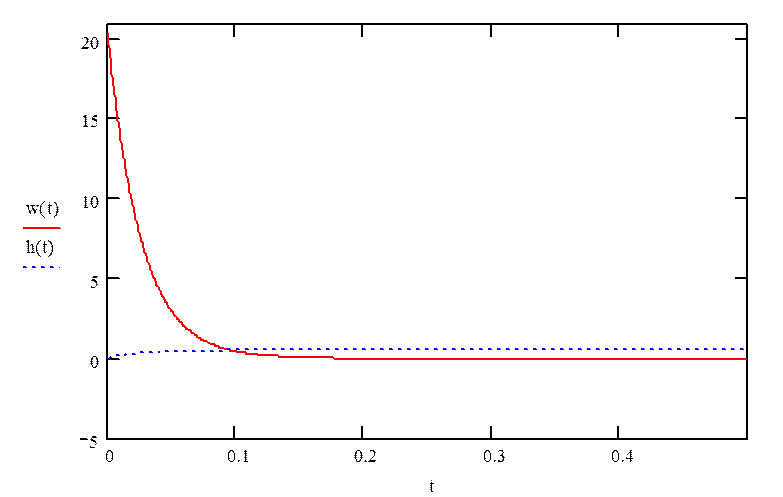
Переходная характеристика будет иметь вид:
рис.3 «График переходного процесса системы»
1.4. Используя символьные вычисления MathCad , получим выражения
и построим графики весовой и переходной характеристик.
рис.4 «График переходного процесса и весовой функции системы»
Как видно из графика, найденные значения весовой и переходной характеристик верны.
1.5. Рассчитаем и построим графики амплитудно-частотной и фазо-
частотной характеристик, логарифмических частотных
Последовательность нахождения частотных характеристик:
— сделать замену в передаточной функции p = j·ω
— освободиться от мнимых чисел в знаменателе
— раскрыть скобки и привести подобные члены, и разделить выражение в числителе на сумму действительного и мнимого полиномов
— записать выражение для действительного и мнимого полиномов
— записать выражение для логарифмической амплитудно-частотной характеристики
— построить графики частотных характеристик.
где U(ω) – вещественная частотная характеристика
V(ω) – мнимая частотная характеристика
Подставим значения коэффициентов:
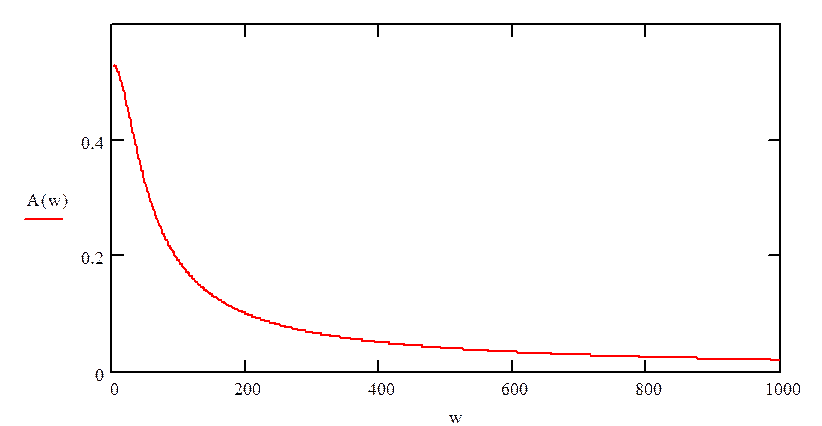
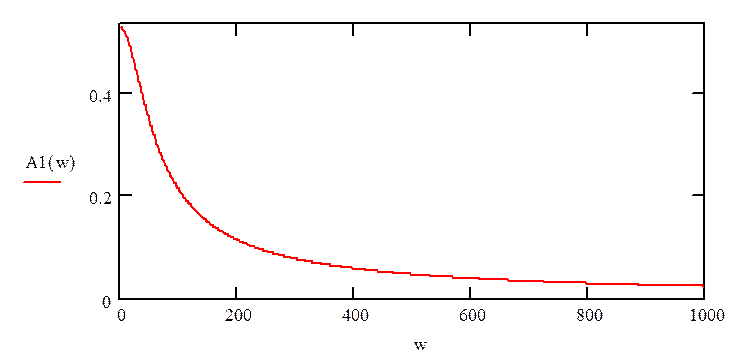
Построим амплитудно-частотную характеристику:
рис.5«График амплитудно-частотной характеристики»
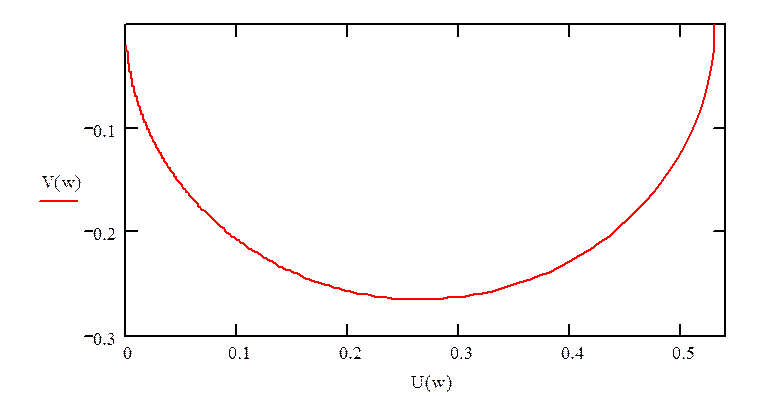
Построим амплитудно-фазовую характеристику (годограф):
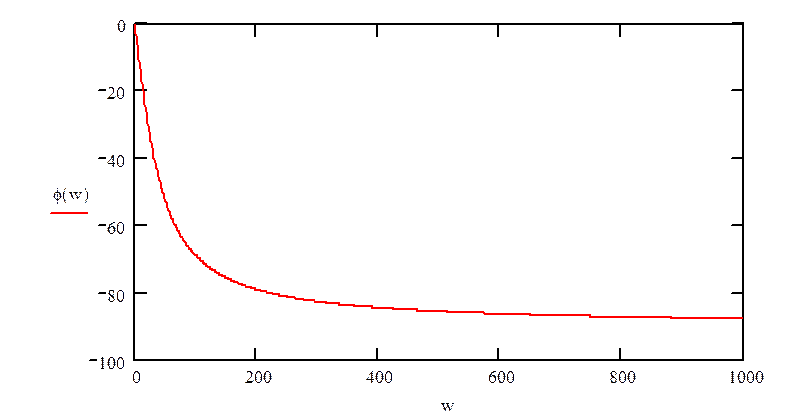
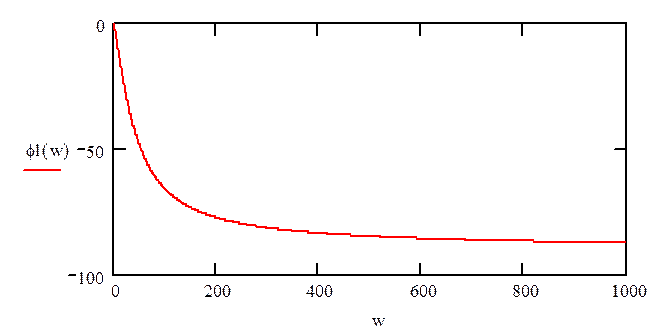
Построим фазо-частотную характеристику:
рис.7«График фазо-частотной характеристики»
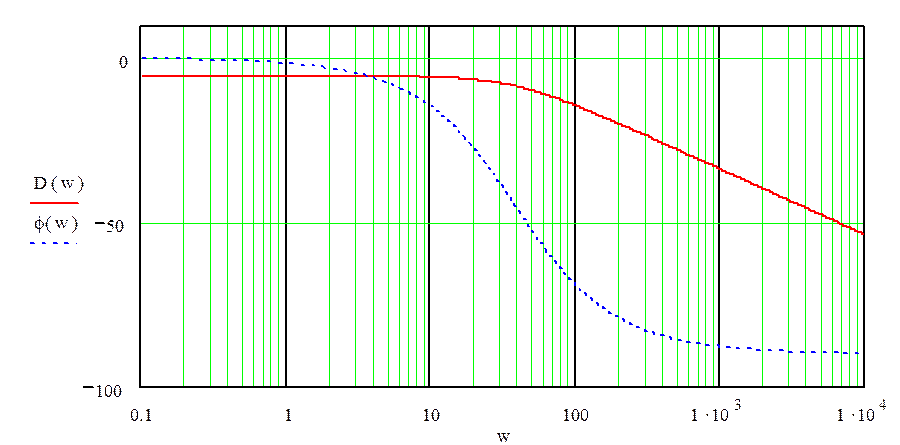
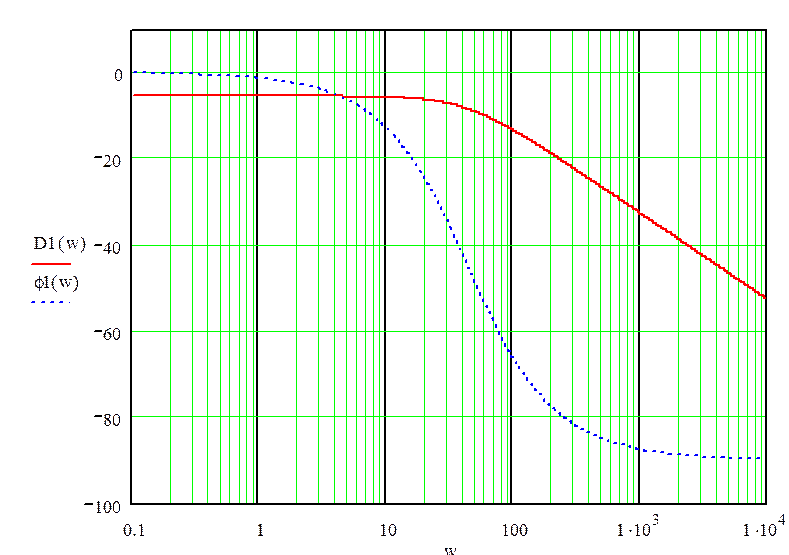
Построим логарифмическую амплитудно-частотную характеристику:
рис.8«График логарифмической амплитудно-частотной характеристики»
Проверим правильность расчетов частотных характеристик устройства с помощью MathCAD.
Запишем выражения для построения частотных характеристик с помощью встроенных функций MathCAD.
рис.9«График амплитудно-частотной характеристики»
рис.10«График фазо-частотной характеристики»
логарифмическая амплитудно-частотная характеристика.
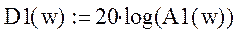
рис.11«График логарифмической амплитудно-частотной характеристики»
Проверка показала, что частотные характеристики объекта управления построены верно.
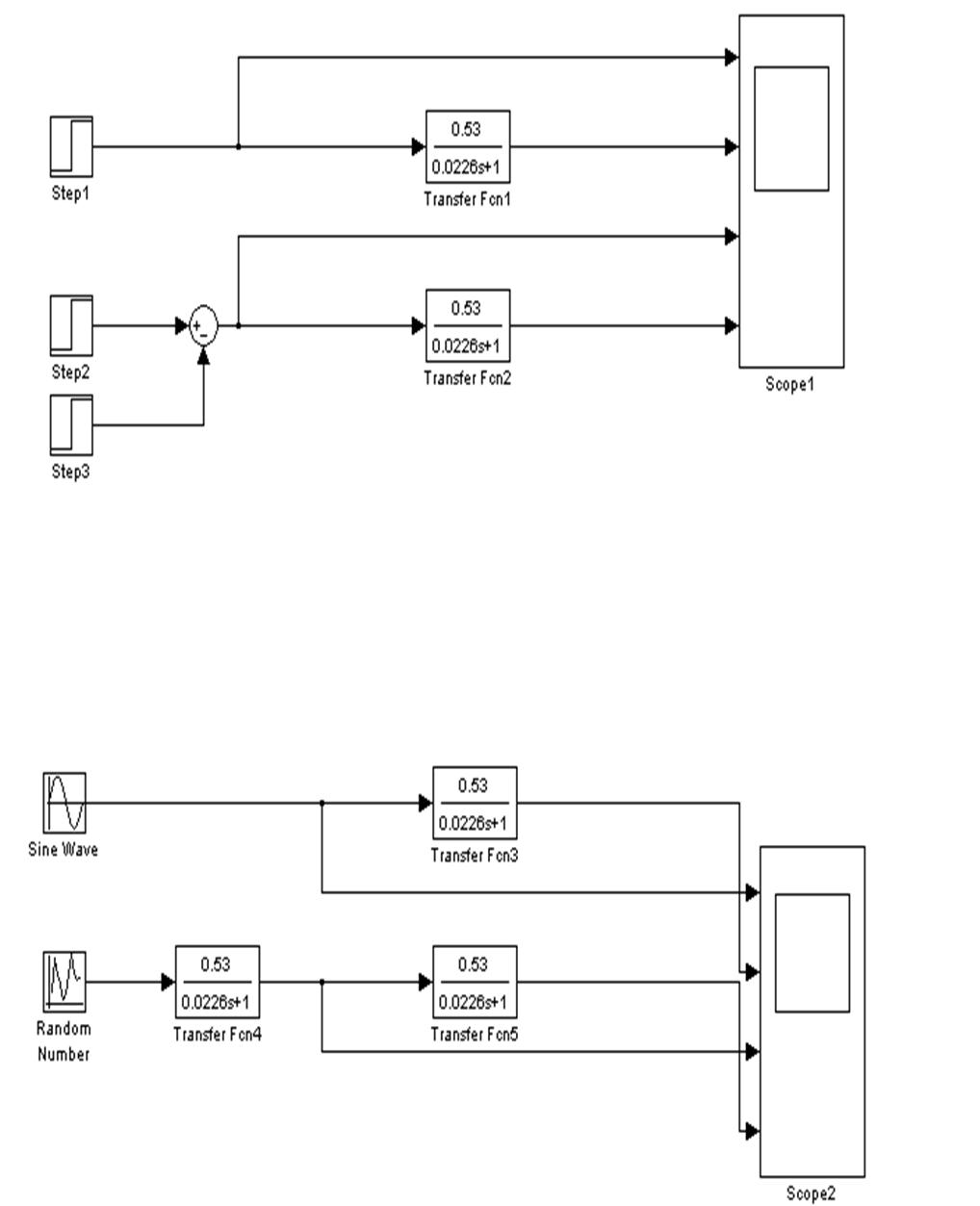
Электропривод можно разделить на две составляющие: электрическую и механическую части. Электрическая часть описывается уравнениями Кирхгофа, а механическая через моменты инерции, нагрузки и сопротивления.
Запишем уравнение для механической части электропривода:
где Мдв – момент на валу двигателя
Мс – момент сопротивления
Запишем уравнение для электрической части электропривода:
где еа – противоЭДС в якоре
— присутствует только при изменении тока в якоре
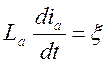
В данном случае инерционность системы определяется моментом инерции J. В связи с этим время переходных процессов мало, поэтому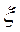 
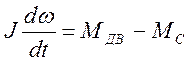
=0.
где Мс = const
Запишем систему уравнений в отклонениях:
 |
(1)
(2)
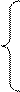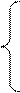
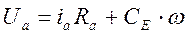
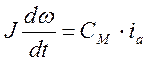
Из уравнения (2) выразим ia и подставим в (1):
(3)
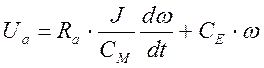
Разделив уравнение (3) на СE, получим:
Получим дифференциальное уравнение, описывающее электропривод:
Следовательно, электропривод является апериодическим звеном первого порядка.
3.2. Найдем передаточную функцию электропривода.
Преобразуем уравнение по Лапласу.
— передаточная функция электропривода по каналу «напряжение якоря – скорость электропривода»
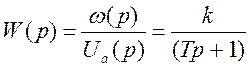
3.3. Определим количественные оценки параметров математической
1. Тип двигателя ДМП 11 (постоянного тока)
2. Номинальная мощность Рн = 2,8 [кВт]
3. Номинальное напряжение якоря Uн = 220 [В]
4. Номинальный ток якоря Iн = 14,5 [А]
5. Номинальный крутящий момент Мн = 14,95 [н·м]
6. Максимальная скорость вращения n = 1790 [об/мин]
7. Момент инерции якоря Ja = 0,04 [кг·м²]
8. Сопротивление обмотки якоря Ra = 7,59 [Ом]
9. Момент инерции нагрузки Jн = 105 [кг·м²]
10. Коэффициент редукции Кред = 120
Рассчитаем коэффициент противоЭДС:
[В·с/рад]
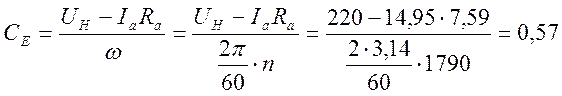
Рассчитаем коэффициент момента:
[кгм/А]
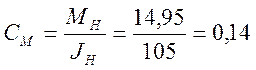
Найдем полный момент инерции:
[кг·м²]
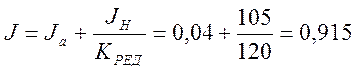
Найдем коэффициенты передаточной функции электропривода:
[с]
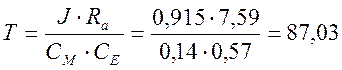
Тогда передаточная функция примет вид:
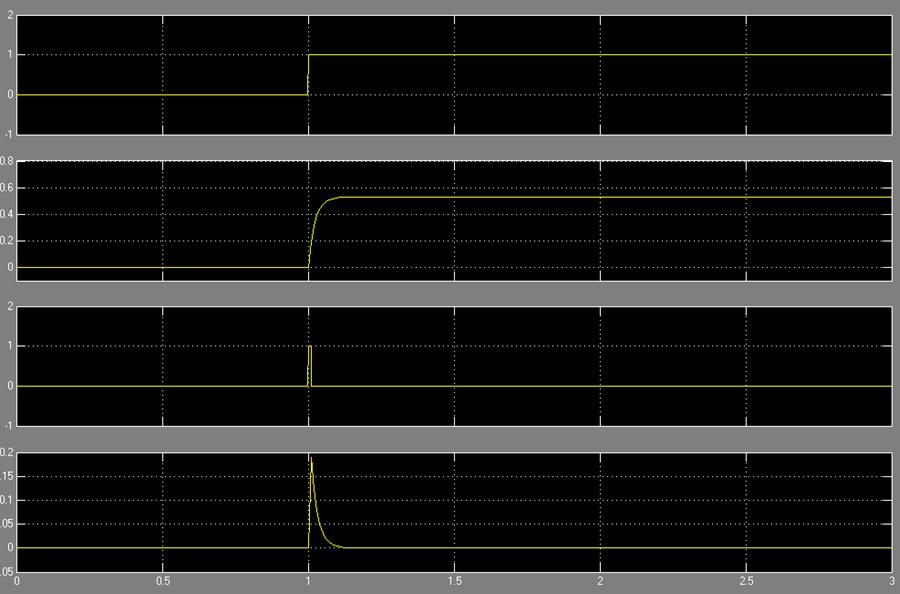
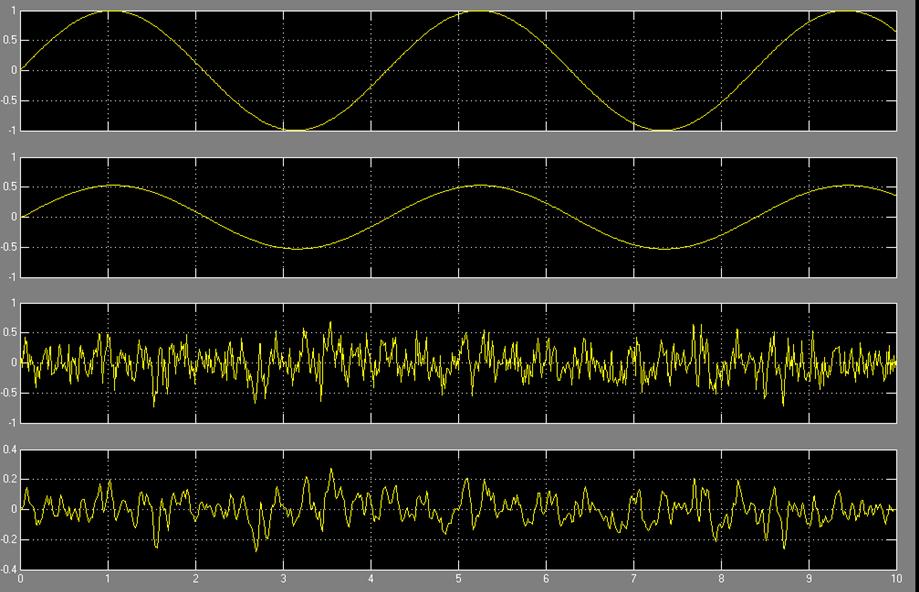
3.4. Построим графики переходных процессов электропривода.
Решив дифференциальное уравнение, описывающее электропривод, получим уравнение движения эл. двигателя при начальной скорости ω0 при входном сигнале Ua.
Рассмотрим три режима работы электропривода:
Чтобы распечатать файл, скачайте его (в формате Word).
Построение переходных процессов
Несмотря на то, что ряд оценок качества функционирования АСР могут быть вычислены без построения таблиц и графиков переходных процессов, тем не менее, окончательный ответ о пригодности системы можно получить только по результатам исследования переходных процессов. Поэтому на завершающей стадии проектирования АСР всегда стремятся тем или иным способом получить оценки динамических характеристик системы и сравнить их с заданными.
При использовании для построения переходных процессов любых методов (аналитические, численные) в качестве исходного материала необходимо иметь математическую модель замкнутой системы в форме передаточной функции, дифференциального уравнения или уравнений АФХ, которые можно получить из передаточной функции.
Если передаточная функция замкнутой системы приведена к дифференциальному уравнению с произвольной правой частью, то аналитическое решение ищется в такой последовательности:
— находятся корни характеристического уравнения;
— строится частное решение с неопределенными коэффициентами;
— это частное решение подставляется в исходное уравнение;
— посредством приравнивания коэффициентов при одинаковых степенях х находятся все неопределенные коэффициенты;
— записывается искомое частное решение.
Это решение и будет являться зависимостью выходной координаты системы от времени.
При использовании численных методов для построения переходных процессов необходимо:
— передаточную функцию замкнутой системы преобразовать в дифференциальное уравнение, разложив при этом звено запаздывания в ряд Паде;
— дифференциальное уравнение n порядка привести к системе из n дифференциальных уравнений первого порядка;
— задать уравнение для возмущающего воздействия;
— выбрать один из численных методов для решения полученной системы; предпочтительнее методы с итерационным уточнением решения на каждом шаге (усовершенствованный метод Эйлера-Коши) или с автоматическим выбором величины шага для обеспечения требуемой точности (метод Рунге-Кутта);
— составить программу для ЭВМ или использовать стандартную из состава математического обеспечения.
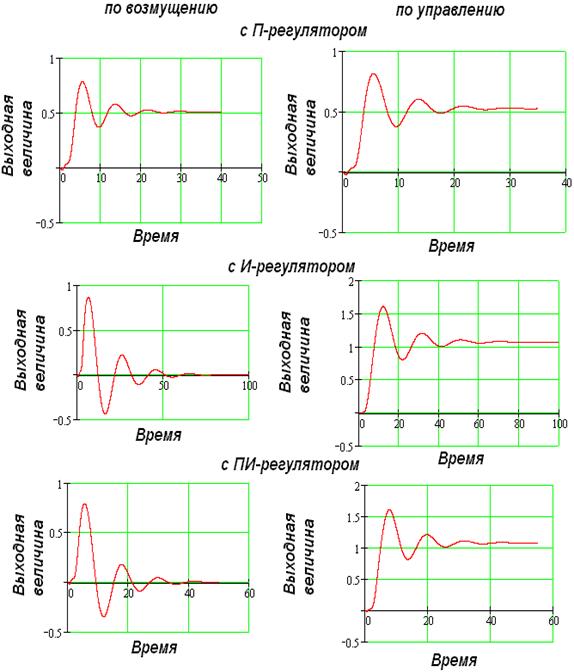
Ниже представлены графики переходных процессов по управлению и возмущению систем с П, И и ПИ-регуляторами. Графики построены в системе MathCad.
Оценка качества функционирования АСР
Как всякая динамическая система, АСР может находиться в одном из двух режимов – стационарном (установившемся) и переходном. Стационарный режим может быть двух типов: статический и динамический. В статическом режиме, при котором все внешние воздействия и параметры системы не меняются, качество управления характеризуется точностью.
Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая процесса. Однако при разработке АСР необходимо иметь возможность судить об основных показателях качества переходного процесса без построения их кривых, по каким-либо косвенным признакам, которые определяются более просто и, кроме того, позволяют связать показатели качества непосредственно со значениями параметров АСР. Такие косвенные признаки называются критериями качества переходного процесса.
Существуют три группы критериев качества: корневые, интегральные и частотные.
Группа корневых критериев основана на оценке качества переходного процесса по значениям полюсов и нулей передаточной функции АСР. В частном случае, когда нулей нет, качество переходного процесса определяется только полюсами.
Переходный процесс в устойчивой системе распадается на затухающие и колебательные составляющие. Если найти длительность самой длительной составляющей и величину колебательности самой колебательной составляющей, то по ним можно оценить верхние пределы величин длительности и колебательности всего переходного процесса.
Интегральными критериями качества называются такие, которые одним числом оценивают и величины отклонений, и время затухания переходного процесса. Такие критерии качества используются для определения оптимальных значений варьируемых параметров по минимуму значения соответствующей интегральной оценки. Применяются интегральные критерии обычно в теории оптимальных систем.
Наибольшее распространение получили частотные критерии, в основу которых положено использование частотных характеристик.
Рассмотрим некоторые критерии качества работы АСР:
1) статическая ошибка – это величина отклонения выходного параметра от заданного значения в установившемся режиме:
если в числителе передаточной функции системы нет свободного члена, то статическая ошибка равна нулю;
2) динамическая ошибка ∂ y – это максимальное отклонение от установившегося значения в переходном процессе;
3) время регулирования – это время tр, за которое выходная координата системы вошла в зону допустимой погрешности регулирования 2∙δ, где δ определяется следующим образом:
4) величина перерегулирования:
5) степень затухания:
учитывая, что 
; с данным критерием тесно связан еще один параметр – степень колебательности системы 
; данные критерии взаимосвязаны следующими соотношениями:
проведя небольшой анализ приведенных соотношений, можно выделить два крайних состояния системы: а) апериодический процесс ψ=1, m =∞; б) незатухающие колебания ψ=0, m =0; часто в расчетах применяют ψ=0.75, m =0.221; все системы регулированию рассчитываются с заданным значением либо ψ, либо m.
АСР считается оптимально настроенной системой, если она удовлетворяет двум или трем критериям качества, например, динамическая ошибка, степень затухания и время регулирования удовлетворяют заданным значениям.
Определим критерии качества для замкнутой АСР по возмущению с П-регулятором. Исходя из графика переходных процессов, статическая ошибка составляет 
, динамическая ошибка: 
.
Чтобы определить время регулирования, рассчитаем сначала допустимую погрешность регулирования: 
.
Таким образом, время регулирования имеет следующее значение 
.
Вычислим величину перерегулирования: 
.
Воспользовавшись заданным значением степени колебательности системы регулирования, определим степень затухания: 
.
Аналогично рассчитываем прямые показатели оценки качества для систем с И и ПИ-регуляторами. Результаты сводим в табл.
Прямые показатели качества АСР
ВЫВОДЫ
1. Статическая модель объекта тем точнее описывает поведение объекта, чем выше порядок полинома.
2. Применительно к динамической модели выяснилось, что ее точность возрастает только до определенного порядка, а затем точность падает.
3. Автоматическая система регулирования с П-регулятором имеет наименьшее значение максимальной динамической ошибки, однако такой системе присуща статическая ошибка, поэтому П-регуляторы могут применяться в случаях, когда допускается отклонение регулируемой величины от заданного значения в равновесном состоянии системы (более 10%).
4. АСР с И-регулятором характеризуется относительно большой динамической ошибкой и перерегулированием, а также длительным переходным процессом, поэтому область применения И-регуляторов ограничивается объектами, допускающими относительно большое максимальное отклонение регулируемой величины. Ни при каких значениях параметров системы И-регулятор не может обеспечить устойчивого регулирования объекта, не обладающего самовыравниванием.
5. АСР с ПИ-регулятором имеет наиболее оптимальные параметры как по динамической ошибке, так и по времени переходного процесса, степени затухания, колебательности и перерегулированию, поэтому ПИ-регуляторы могут применяться при любых требованиях к значению установившегося отклонения и любом диапазоне возмущающих воздействий, если допустимое время регулирования значительно.
ЛИТЕРАТУРА
Дата добавления: 2019-07-15 ; просмотров: 1064 ; Мы поможем в написании вашей работы!