Как построить график параболы по уравнению
График квадратичной функции (ЕГЭ 2022)
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция.
Проверь себя, ответь на эти вопросы:
Если ты сходу смог ответить, продолжай читать.
Если хоть один вопрос вызвал затруднения, повтори тему «Квадратичная функция».
График квадратичной функции — коротко о главном
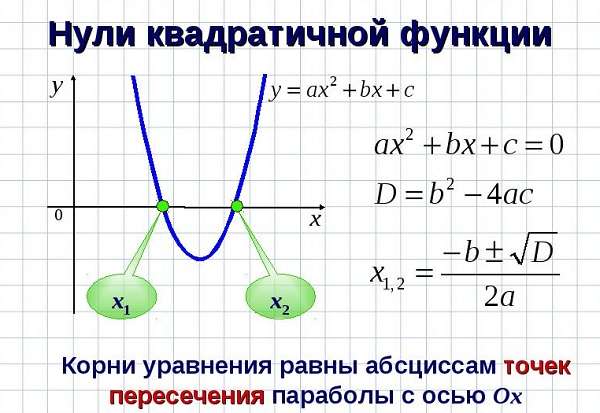
Определение
Квадратичная функция – функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
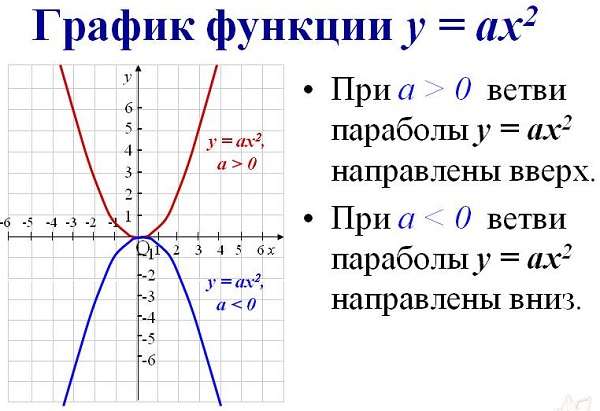
График квадратичной функции – парабола.
Если коэффициент \( \displaystyle a 0\) – ветви параболы направлены вверх.
Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.
Вершина параболы
\( \displaystyle <
Подставляем \( \displaystyle <
\( \displaystyle <
Свободный член \( \displaystyle c\) – это координата пересечения параболы с осью ординат.
Квадратичная функция и её коэффициенты
Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
Ну что же, вот она: \( y=a<
Давай вкратце вспомним, что делают коэффициенты.
С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?
Это вершина. А как найти координаты вершины, помнишь?
Абсцисса ищется по такой формуле:
Вот так: чем больше \( \displaystyle b\), тем левее смещается вершина параболы.
Ординату вершины можно найти, подставив \( <
Подставь сам и посчитай. Что получилось?
Если сделать все правильно и максимально упростить полученное выражение, получится:
Получается, что чем \( \displaystyle b\) больше по модулю, тем выше будет вершина параболы.
Перейдем, наконец, к построению графика.
Самый простой способ – строить параболу, начиная с вершины.
Пример №1
Построить график функции \( y=\frac<1><2><
Решение:
Для начала определим коэффициенты: \( a=\frac<1><2>;\text< >b=2;\text< >c=-1\).
Теперь вычислим координаты вершины:
А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково.
Остается только один вопрос. Как быстро рисовать параболу?
Как быстро рисовать график квадратичной функции — параболу?
Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?
Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить. Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.
Рассмотрим простейшую параболу \( y=<
Закономерность здесь такая.
Если из вершины сместиться вправо (вдоль оси \( \displaystyle Ox\)) на \( \displaystyle 1\), и вверх (вдоль оси \( \displaystyle Oy\)) на \( \displaystyle 1\), то попадем в точку параболы.
Дальше: если из этой точки сместиться вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 3\), снова попадем в точку параболы.
Дальше: вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 5\). Дальше что?
Вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 7\).
И так далее: смещаемся на \( \displaystyle 1\) вправо, и на следующее нечетное число вверх.
То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным \( \displaystyle 1\).
Пример построения параболы быстрым способом
Например, нам стало известно, что вершина параболы находится в точке \( \displaystyle \left( 1;-2 \right)\). Построй (самостоятельно, на бумаге) эту параболу.
Должно получиться так:
Теперь соединяем полученные точки:
ОК, ну что же, теперь строить только параболы с \( \displaystyle a=1\)?
Конечно, нет. Сейчас разберемся, что с ними делать, если \( \displaystyle a\ne 1\).
Три типичных случая построения параболы
Cлучай 1. \( a=-1\).
То есть функция выглядит как \( y=-<
И то же самое, только влево.
Случай 2. \( a>1\).
Что делать, если, например, \( a=2\)?
Все просто: начинаем так же: \( 1\) вправо, но когда дело доходит до «вверх», любое число увеличиваем в \( 2\) раза:
Аналогично в случае \( a
Как построить параболу
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле
Построить график функции y=x²+2x-3.
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
Построить график функции y=x²+5x+4.
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Вершина (-1,5; 2,25) — первая точка параболы.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x ² +c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Парабола свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
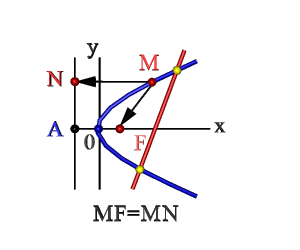
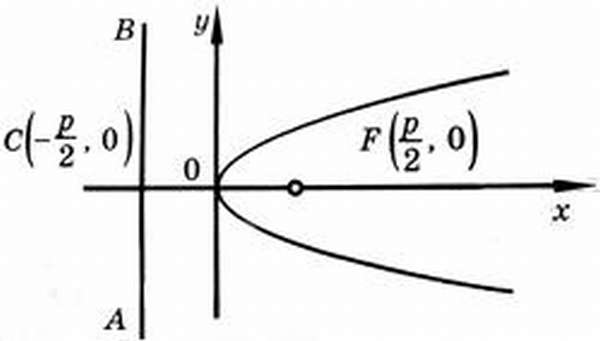
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
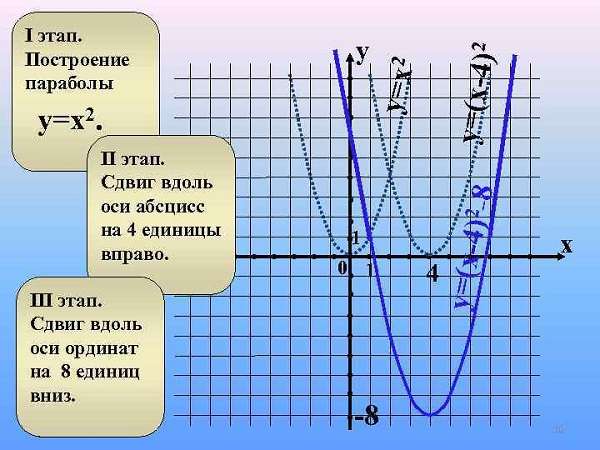
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
Получаем алгоритм построения параболы:
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
По полученным точкам можно построить параболу.
Директриса, эксцентриситет, фокус параболы
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Эксцентриситет (константа) = 1.
Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс: