Как построить график кусочно заданной функции
Урок-мастерская по теме «Построение графика кусочной функции в табличном процессоре Excel по заданным параметрам»
План проведения мастерской:
1. Организационный момент.
Учащиеся проходят в класс. Занимают свои места. Учителя приветствуют их.
2. Актуализация знаний.
На доске записано слово “Функция”. Учитель математики просит учащихся назвать ассоциации, связанные с этим словом.
3. Подготовительная работа.
Учащимся предлагается 4 вида графиков и варианты функций. Соотнести графики функций с их алгебраической записью.
Графики и алгебраические записи размещены на маркерной доске.
 | y= √х |
 | y = | х| |
 | y = x 2 |
 |  |
Учащимся предлагается 4 вида преобразования графиков. Необходимо объяснить, какой вид преобразования используется (данное задание учитель математики иллюстрирует, используя электронное сопровождение курса “Алгебра – 8” под редакцией А.Г.Мордковича).
4. Поиск подхода к решению задачи.
Каждый ученик получает карточку определённого цвета, на которой представлена часть того или иного графика. Учащиеся делятся на группы по цветам.
– Соедините части и скажите, что у Вас получилось? (График кусочной функции)
– Как построить график кусочной функции? Попробуйте вспомнить алгоритм.
5. Работа в группах.
Каждая группа получает конверты с заданиями. Учащиеся внутри группы сами определяют, кто и какую часть будет строить. Построив каждый кусочек функции на листе, учащийся выполняет построение на компьютере под руководством учителя информатики.
Необходимо построить таблицу значений “х” и “у”, заполнить для заданного интервала, самостоятельно выбрав шаг.
Для заполнения значений “у” необходимо правильно внести формулы в ячейку таблицы. (Памятка 2.)
Каждый ученик строит согласно своему заданию функцию и сохраняет работу на отдельном листе книги Excel, переименовав его согласно номеру задания.
Далее все части собираются на одном листе, а затем на компьютере. Если группы справились с заданием, то и на листе, и на компьютере графики одинаковы.
6. Обсуждение в мастерской.
Работы вывешиваются на доску. Учащиеся сравнивают полученный график с макетом, собранным ими в начале урока. Оценивают работы друг друга. Высказывают свои мнения.
Группа 1 получила после выполнения задания график вида:
Группа 2 получила после выполнения задания график вида:
Группа 3 получила после выполнения задания график вида:
Группа 4 получила после выполнения задания график вида:
7. Оценочно-рефлексивная деятельность.
Каждому ученику предлагается оценить свои чувства после выполнения работы. Для этого, на доске расположены 3 рисунка. Каждый ученик подходит к доске и прикрепляет к выбранному им рисунку клейкую бумагу. В конце подсчитывается количество прикреплённых бумажек к тому или иному рисунку. Обсуждается, почему выбрано то или иное настроение.
В конце урока каждому ученику вручается сертификат и выполненная им работа.
Кусочные функции. Как построить график кусочной функции
Кусочными функциями называют функции, которые заданы разными формулами на разных промежутках.
Другими словами, на различных участках числовой прямой функция ведет себя по разным законам.
Пример. Построить график кусочной функции \(y=\begin
Отметим их на координатной плоскости:
2) Построим вторую функцию на области \(x∈(-1;∞)\).
Для начала проверим «состыкуются» ли графики, для этого найдем значение функции \(y=x^2-4x\) в точке \(-1\):
\(y(-1)=(-1)^2-4\cdot(-1)=1+4=5\) – значение такое же, как в первой функции, значит графики состыкуются.
Отметим эту точку на графике и проведем через неё ось симметрии параболы.
Найдем значение в точке \(1\) и \(0\):
\(y(1)=1^2-4\cdot 1=1-4=-3\)
\(y(0)=0^2-4\cdot 0=0\)
Отметим точки \((1;-3)\), \((0;0)\) и симметричные им на координатной плоскости.
Соединим первый график и получившиеся точки в одну плавную линию.
Готово. График кусочной функции построен.
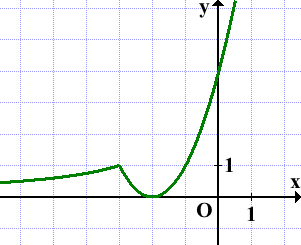
Как не должна выглядеть кусочная функция:

Здесь парабола заехала на территорию гиперболы, а гипербола заехала на территорию параболы, так быть не должно! У каждого кусочка – своя территория.
График кусочно заданной функции
Построить график кусочно заданной функции — один из видов задания 23 из ОГЭ по математике.
Рассмотрим примеры построения таких графиков.
1) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Область определения функции D(y): x∈R.
График данной функции состоит из трёх частей.
Значения x=3 и x=4 разбивают числовую прямую на три промежутка, на каждом из которых рассмотрим отдельную функцию.
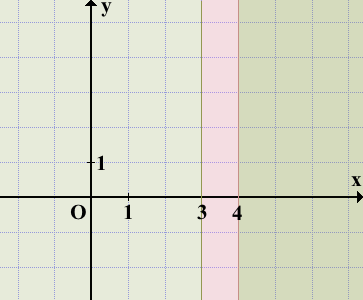
Соответственно, прямые x=3 и x=4 разбивают координатную плоскость на три области.
Каждый из графиков строится в своей области и не должен выходить за её пределы.
Чтобы не нарушить это правило, можно прямые x=3 и x=4 (прямые, параллельные оси Oy) выделить на черновике тонкой линией либо пунктиром. В чистовой вариант, разумеется, их переносить не нужно.
Итак, рассмотрим на трёх промежутках три различные функции.
1) Если x
Значения x можно брать, вообще говоря, любые. Главное, не забыть, что данная прямая не должна выходить правее x=3. Поэтому всё же лучше выбирать x, удовлетворяющие условию x
y=1,5x-5 — линейная функция. График — прямая. для построения прямой берём две точки.
Отметим каждую пару точек и проведём через них прямые, не забывая об ограничениях.
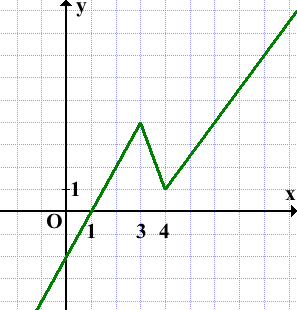
Получим график, состоящий их двух лучей и одного отрезка:
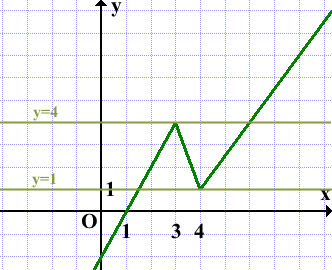
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через точки соединения двух частей графика, то есть при m=1 и m=4:
2) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Область определения функции D(y): x∈R.
y=x²-10x+27 — квадратичная функция. Её график — парабола, ветви которой направлены вверх (так как a=1>0).
Таким образом, (5;2) — вершина параболы.
Так как a=1, от вершины строим параболу y=x².
(Другой вариант — переписать правую часть формулы в виде y=(x²-10x+25)+2=(x-5)²+2 и построить график параллельным переносом графика y=x² на 5 единиц вправо вдоль оси Ox и на 2 единицы вверх вдоль оси Oy).
2) Если x
Хотя на x наложено условие x
и определить, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Область определения функции D(y): x∈R.
y=x²+4x+4 — квадратичная функция. График — парабола ветвями вверх. Можно найти координаты вершины параболы и от вершины построить график функции y=x².
(Если заметить в правой части формулу квадрата суммы и переписать формулу функции y=(x+4)², то можно построить параболу параллельным переносом параболы y=x² на 4 единицы влево вдоль оси Ox).
2) Если x
Таким образом, график данной функции состоит из двух частей. Справа от прямой x=-3 строим параболу с вершиной в точке (-2;0), слева — ветвь гиперболы:
Прямая y=m имеет с графиком одну или две общие точки при m=0 и m≥1:
Кусочно-линейная функция
Графики и формулы кусочно-линейных функций
На практике в течение некоторого времени тело может двигаться, потом – покоиться, потом – опять прийти в движение, но уже с другой скоростью и в другом направлении и т.п. Как задать подобную зависимость?
Допустим, турист идет из начальной точки по прямой тропинке в течение 2 ч со скоростью 5 км/ч, затем останавливается отдохнуть на 1ч и возвращается обратно по той же тропинке со скоростью 4 км/ч. Нам нужно найти формулу для расстояния s(t) от начальной точки на протяжении всего похода.
Изобразим зависимость s(t) графически:
Важным свойством заданной функции является выполнение условий согласования:
$$ s_1 (2) = s_2 (2) = 10,s_2 (3) = s_3 (3) = 10$$
Наша функция «сшита» на концах промежуточных интервалов.
$$x f(x) = <\left\< \begin
При этом для функции на краях интервалов выполняются условия согласования:
Графиком кусочно-линейной функции является ломаная линия
Знак модуля в линейных функциях
Если в формуле для линейной функции содержится знак модуля, то после его раскрытия получается кусочно-линейная функция.
Примеры
Пример 1. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:
Пример 2*. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:
Как видно из этого примера, аналитически выводить формулу для двух модулей очень нелегко.
Гораздо легче сразу построить график, если следовать следующим простым правилам преобразования.
Шаг 1. Строим y = 2x-1
Лекция по теме «Как строить график кусочной функции»
Как построить график кусочной функции
Кусочные функции — это функции, заданные разными формулами на разных числовых промежутках. Например,
Чтобы построить график такой кусочной функции, сначала строятся графики двух разных функций не зависимо от значения x (т. е. на всей числовой прямой аргумента). После этого от полученных графиков берутся только те части, которые принадлежат соответствующим диапазонам x. Эти части графиков объединяются в один. Понятно, что в простых случаях чертить можно сразу части графиков, опустив предварительную прорисовку их «полных» вариантов.
Для приведенного выше примера для формулы y = √x получим такой график:
Здесь x в принципе не может принимать отрицательных значений (т. е. подкоренное выражение в данном случае не может быть отрицательным). Поэтому в график кусочной функции уйдет весь график уравнения y = √x.
В данном случае в кусочную функции мы возьмем только ту часть параболы, для которой x принадлежит промежутку (–∞; 0). В результате получится такой график кусочной функции:
Рассмотрим другой пример:
Графиком функции f(x) = (0.6x – 0.5) 2 – 1.7 будет видоизмененная парабола. Графиком f(x) = 0.5x + 1 является прямая:
В кусочной функции x может принимать значения в ограниченных промежутках: от 1 до 5 и от –5 до 0. Ее график будет состоять из двух отдельных частей. Одну часть берем на промежутке [1; 5] от параболы, другую — на промежутке [–5; 0] от прямой: