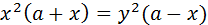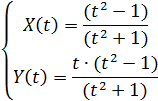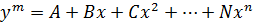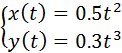Как построить график функции заданной параметрически
Построение графика функции, заданной в параметрической форме.
Государственное образовательное учреждение высшего профессионального образования
Московский авиационный институт
(национальный исследовательский университет)
РАДИОВУЗ МАИ
О.М.Данченко
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
МОСКВА
Данное пособие содержит типовые задачи для индивидуальных заданий студентов-заочников по курсу «Математический анализ» часть 1. Ко всем задачам приводятся подробные решения и указания. Приведенные задания в равной степени могут использоваться студентами очного отделения при подготовке к экзамену. В приложении приведена подробная программа курса по «Математическому анализу» часть 1.
Содержание
Построение графиков функций, заданных в полярной системе координат или в параметрической форме……………………………………………………………
Вычисление пределов последовательностей и функций…………………………
Исследование функций на непрерывность………………………………………..
Исследование функций с помощью производных, построение графиков функций……………………………………………………………………………..
Задания на вычисление интегралов……………………………………………….
Введение
В процессе изучения курса «Математический анализ» предусмотрено выполнение студентами индивидуальных домашних заданий в каждом семестре. Индивидуальное домашнее задание 1-ого семестра содержит следующие задачи:
1. Построение графиков функций, заданных в полярной системе координат или заданных в параметрической форме.
2. Вычисление пределов последовательностей и функций.
3. Исследование функций на непрерывность.
4. Вычисление производных от сложных функций, функций, заданных неявно или в параметрической форме.
5. Исследование функций с помощью производных, построение графика функции.
6. Вычисление неопределенного и определенного интегралов.
Рассмотрим далее типовые примеры на каждое из заданий и укажем методы их решения.
Построение графиков функций, заданных в простой полярной системе координат.
Простая полярная система координат характеризуется следующим:
ρ=ρ(φ); 0≤ρ
а) указать область допустимых значений (О.Д.З.), т.е. определить при каких углах φфункция ρ(φ) – неотрицательна, т.е. ρ(φ)≥ 0;
б) найти область изменения функции;
в) указать является ли функция четной или нечетной, т.е. если ρ(-φ) = ρ(φ),то график функции симметричен относительно полярной оси и, следовательно, достаточно сделать исследования для φ≥0.После данных исследований следует построить кривую по точкам.
Пример: построить график функции в простой полярной системе координатρ=2cos2φ
Так как в простой полярной системе координат ρ≥0, то О.Д.З. будут являться только те углы φ,для которых cos2φ≥0,т.е. 0≤φ≤π/4; 3π/4≤φ≤5π/4; 7π/4≤φ≤2π. Функция будет ограничена, т.к. |cos2φ|≤1,т.е. |2cos2φ|≤2. Так как функция четная и периодическая то достаточно построить кривую только для 0≤φ≤π/4, а затем отразить кривую симметрично относительно полярной оси и в силу периодичности построить аналогичную петлю для 3π/4 ≤φ≤5π/4.Для 0≤φ≤π/4функция монотонно убывает от двух до нуля, для 3π/4≤φ≤πфункция монотонно возрастает от нуля до двух (рис. 1).
Построение графика функции, заданной в параметрической форме.
Пусть x=X(t)и y=Y(t), где параметр tизменяется в определенных заданных пределах. График функции, заданной в параметрической форме, строится по характерным точкам.
Пример: x=t², y= t∙(t²-3)/3
а) Заметим, что для любых значений аргумента t функция x(t)=t²≥0, следовательно, график функции расположен в правой полуплоскости.
б) В силу нечетности функции y(t), так как y(-t)=-y(t), график функции симметричен относительно оси ОХ.
в) Определим точки, в которых y(t) = 0: при t=0, y(0)=0 и x(0)=0
Построение графиков функций, заданных в параметрической форме
Задание функции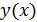 
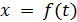
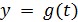
с помощью равенств 
и 
называют
параметрическим, а вспомогательную величину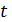 
— параметром.
Для построения графика функции, заданной параметрически, необходимо определить массив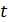 
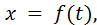
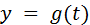
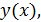
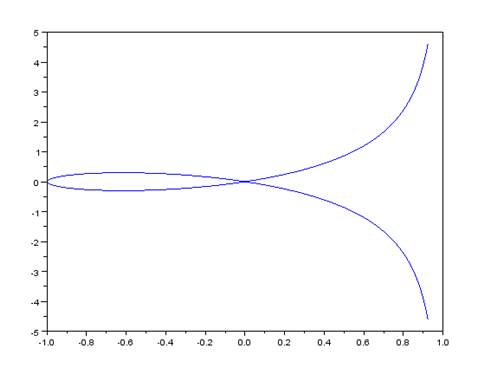
, определить массивы 
и построить график функции 
используя функции plot(x,y) либо plot2d(x,y).
Пример. Построить график строфоиды.
Напомним, что строфоида представляет собой алгебраическую кривую третьего порядка, которая в общем виде задается уравнением:
Представим это уравнение с помощью параметра t:
Зададим массивы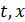 
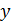
и 
и построим график с помощью функции plot(x,y)
Пример. Построить график полукубической параболы.
Полукубическая парабола-это алгебраическая кривая второго порядка, которая в общем виде может быть описана следующим уравнением:
Приведем это уравнение к параметрической форме:
Как и в примере со строфоидой,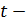 
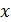
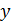
параметр определяем как массив, а 
и как зависимые от него величины. Однако теперь для построения графика обратимся к функции plot2d(x,y)
Как построить график кривой заданной параметрически mathcad
Построить кривую заданную параметрически
Изобразить на плоскости кривую, заданную параметрически, касательную и нормаль к ней в указанной точке М
Изобразить на плоскости кривую, заданную параметрически, касательную и нормаль к ней в указанной.
Изобразите на плоскости кривую, заданную параметрически, и касательную и нормаль к ней в указанной точке
Задание: Изобразите на плоскости кривую, заданную параметрически, и касательную и нормаль к ней в.
Постройте кривую заданную в полярной системе координа
Помогите решить! Постройте кривую, заданную в полярной системе координа.
Построить график параметрически заданной функции.
построить график параметрически заданной функции при значениях констант a,b и лямда. фи меняется от.
построить кривую
помогите пожалуйста построить кривую заданную уравнением
Провести исследование и построить график кривой заданной параметрически
Здравствуйте,помогите пожалуйста. Провести исследование и построить график кривой заданной.
Реферат: Построение поверхностей в Mathcad и Maple
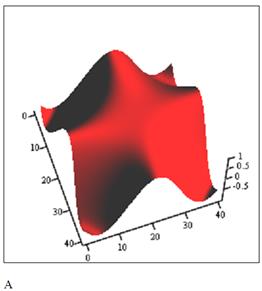
Быстрое построение является наиболее легким способом построения поверхностей. Для этого необходимо:
1. На лист Mathcad ввести формулу z(x,y):=…;
2. Выбрать команду главного меню «Вставка», «График», выбрать вид графика «поверхность» на панели инструментов «Графики».
3. В шаблон трехмерного графика ввести имя функции без указания аргументов.
Построение поверхностей по матрице аппликат.
Самый «правильный» способ построения графика поверхности, заданной функцией от двух переменных z = f(x,y), является заполнение матрицы значениями этой функции. При этом строки и столбцы матрицы интерпретируются как абсциссы и ординаты. Пример:
Число линий для построения графика и масштаба N:=40 M:=40
Определение индексов i:=0..N j:=0..N
Определение массивов абсцисс и ординат xi := yj :=
В шаблон трехмерного графика вводим название массива аппликат:
Построение с помощью функции CreateMesh.
Функция CreateMesh относится к категории Vectorandmatrix (Векторы и матрицы), так как результатом работы функции будет матрица координат.
Формат вызова функции:
Параметры функции CreateMesh:
Mesh – количество линий в сетке функции;
F – вид функции (может быть или формула, или трёхмерный вектор, задающий каждую координату в параметрической форме, или три отдельные функции, задающие координаты в параметрическом виде);
— x1 – нижняя граница переменной x;
— x2 – верхняя граница переменной x;
— y1 – нижняя граница переменной y;
— y2 – верхняя граница переменной y;
— xgrid – количество точек переменной х;
— ygrid – количество точек переменной y.
В одной системе координат можно построить несколько поверхностей, для этого достаточно определить их, а затем в шаблон графика ввести их имена без аргументов через запятую:
Построение одного и того же графика в декартовой, цилиндрической
и сферической системах координат
Пусть задана какая-нибудь функция, например z(x,y)=const. В различных системах координат эта функция имеет различные графики. В декартовой системе координат это плоскость, параллельная плоскости Оху, в цилиндрической – прямой круговой цилиндр с основанием радиуса const, в сферической – шар радиуса const. Для изменения системы координат, надо по шаблону графика щелкнуть правой кнопкой мыши, в появившемся перечне выбрать «Свойства», затем «Данные QuickPlot» и указать нужную систему координат. Пример:
Для построения многогранников в Mathcad есть функция Polyhedron. Её можно использовать двумя способами:
1) по имени, тогда обращение к функции будет Polyhedron(“имя многогранника”);
2) по коду, тогда обращение к функции будет Polyhedron(“#номер многогранника”).
Построение поверхностей вращения.
Для построения поверхностей вращения в Mathcad удобно использовать функцию CreateMesh.
Параметры функции CreateMesh:
— x1, y1,z1 – матрицы значений для каждой координаты;
— 5 – верхняя граница переменной u;
— 0 – нижняя граница переменной v;
— 2π – верхняя граница переменной v;
— 30 – количество линий в сетке графика.
Параметрические уравнения для поворота вокруг оси Ох:
Параметрические уравнения для поворота вокруг оси Oy:
Пример: рассмотрим гиперболу y 2 – x 2 = 1. При вращении этой гиперболы вокруг оси Ох получается однополостный гиперболоид, при вращении вокруг оси Оу – двуполостный гиперболоид. Построим эти поверхности вращения:
Построение пространственных линий.
Линия в пространстве, рассматриваемая как след движущейся точки, представляется системой трёх уравнений: x = x(t); y = y(t); z = z(t), выражающих координаты точки t. Эти уравнения называются параметрическими уравнениями пространственной линии. Для построения пространственных линий в Mathcad существует функция CreateSpace.
Функция CreateSpace относится к категории Vector and matrix (Векторы и матрицы), так как результатом работы функции будет матрица координат. Работает аналогично CreateMesh. Главное отличие в том, что параметрические уравнения должны быть функциями одной переменной, а не двух, как в CreateMesh. Вызов функции: CreateSpace(F, t1, t2, tgrid). Параметры функции:
— F – вектор параметрических уравнений координат;
— t1 – нижняя граница переменной;
— t2 – верхняя граница переменной;
— tgrid – число линий сетки; не обязательный параметр; чем больше этот параметр, тем более гладкая получается линия; если он не достаточно велик, линия получается с изломами.
Maple. Построение поверхностей и пространственных линий.
График поверхности, заданной явной функцией.
График поверхности, заданной неявно.
Пример: построим поверхность Очевидно, что функция задана неявно, поэтому используем алгоритм, описанный выше.
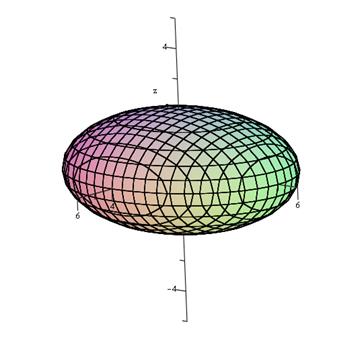
График поверхности, заданной параметрически.
График пространственных кривых.
Пример: построить пространственную кривую, заданную параметрически х = arctg(t),
В Maple также существует возможность построения нескольких графиков одновременно. Для этого необходимо задать каждую поверхность, а затем использовать команду display. Пример:
Для построения поверхностей вращения в Maple есть функция Surface of revolution. Чтобы ей воспользоваться нужно во вкладке «Tools» выбрать раздел «Tutors», затем подраздел «Сalculus – SingleVariablе», функцию «Surface of revolution». В появившемся окне надо ввести функцию, интервал на котором будет произведено построение, выбрать ось вращения и параметры графика. Окно графика появляется при нажатии кнопки «Close».
Пример: построим поверхности, полученные вращением графика функции y=sin x на интервале от 0 до π вокруг оси Ох и Оу. Вызываем функцию Surface of revolution как описано выше. В поле «f(x)» вводим sin(x), указываем границы интервала, в поле Line of Revolution в одном случае выбираем Vertical, в другом Horizontal, нажимаем Сlose.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Построение кривых второго порядка в среде Mathcad
Построение кривых на плоскости, заданных в декартовых координатах в системе Mathcad.
Для построения графиков используются шаблоны. Их можно выбирать двумя способами.
1 Выбор шаблона с помощью подменю График в меню Вставка (рисунок 17)
2. Выбор шаблона с помощью панелей инструментов. Для этого в панели Math необходимо щелкнуть по кнопке Graph (инструменты графиков) 
(рисунок 18). Затем щелчком по кнопке панели Graph вставить поле графика соответствующего типа (рисунок 19).
Незаполненный шаблон графика представляет собой большой пустой прямоугольник с шаблонами-местами ввода данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика. В них необходимо ввести выражения, задающие координаты точек графика по осям абсцисс и ординат. В общем случае это могут быть функции некоторой переменной x.
Рисунок 18 Рисунок 19
Если график уже построен, то при его выделении появляются крайние места ввода с автоматически введенными числами, которые служат для указания предельных значений абсцисс и ординат, то есть задают масштаб графика. Сначала рекомендуется использовать автоматическое масштабирование, а лишь затем выбирать более походящий масштаб.
Особое внимание при построении графика следует уделить заданию пределов изменения переменной x. Различают упрощенный способ без задания ранжированной переменной, при котором пределы изменения задаются автоматически, и обычный способ с заданием ранжированной переменной. Упрощенный способ был рассмотрен ранее. При обычном способе необходимо ввести саму функцию и интервал её изменения, а лишь затем выбирать шаблон.
Форматирование двухмерных графиков.
Вид графика можно изменять при помощи команд форматирования графиков. Для изменения формата уже построенного графика необходимо его выделить, щелкнув по нему. Выделенный график обводится сплошной линией с маркерами изменения размера.
Затем к выделенному графику можно применить команду Формат из главного меню и выбрать и выбрать в ней подменю график (рисунок 20). При этом появляется диалоговое окно форматирования (рисунок 21).
Это же диалоговое окно появится, если щелкнуть по выделенному графику правой копкой мыши и выбрать в появившемся меню подменю Формат или дважды щелкнуть левой кнопкой мыши по графику.
Рисунок 20
Диалоговое окно форматирования имеет четыре вкладки:
Оси X-Y – задание параметров отображения осей;
Трассировки (Линии) – задание параметров отображения линий графика;
Метки – задание параметров отображения меток (надписей) у осей;
Умолчание – задание параметров по умолчанию.
Все параметры форматирования относятся к выделенному графику и могут при необходимости меняться.
Задание 2. Построить в одной системе координат графики трех функций. Решение задания на рисунке 24.
В пакете Mathcad также возможно построение кривых, заданных в полярных координатах и в параметрической форме. Примеры таких построений приведены на рисунках 28 и 29.
Как построить график кривой заданной параметрически mathcad
Построить кривую заданную параметрически
Изобразить на плоскости кривую, заданную параметрически, касательную и нормаль к ней в указанной точке М
Изобразить на плоскости кривую, заданную параметрически, касательную и нормаль к ней в указанной.
Изобразите на плоскости кривую, заданную параметрически, и касательную и нормаль к ней в указанной точке
Задание: Изобразите на плоскости кривую, заданную параметрически, и касательную и нормаль к ней в.
Постройте кривую заданную в полярной системе координа
Помогите решить! Постройте кривую, заданную в полярной системе координа.
Построить график параметрически заданной функции.
построить график параметрически заданной функции при значениях констант a,b и лямда. фи меняется от.
построить кривую
помогите пожалуйста построить кривую заданную уравнением
Провести исследование и построить график кривой заданной параметрически
Здравствуйте,помогите пожалуйста. Провести исследование и построить график кривой заданной.
Реферат: Построение поверхностей в Mathcad и Maple
Быстрое построение является наиболее легким способом построения поверхностей. Для этого необходимо:
1. На лист Mathcad ввести формулу z(x,y):=…;
2. Выбрать команду главного меню «Вставка», «График», выбрать вид графика «поверхность» на панели инструментов «Графики».
3. В шаблон трехмерного графика ввести имя функции без указания аргументов.
Построение поверхностей по матрице аппликат.
Самый «правильный» способ построения графика поверхности, заданной функцией от двух переменных z = f(x,y), является заполнение матрицы значениями этой функции. При этом строки и столбцы матрицы интерпретируются как абсциссы и ординаты. Пример:
Число линий для построения графика и масштаба N:=40 M:=40
Определение индексов i:=0..N j:=0..N
Определение массивов абсцисс и ординат xi := yj :=
В шаблон трехмерного графика вводим название массива аппликат:
Построение с помощью функции CreateMesh.
Функция CreateMesh относится к категории Vectorandmatrix (Векторы и матрицы), так как результатом работы функции будет матрица координат.
Формат вызова функции:
Параметры функции CreateMesh:
Mesh – количество линий в сетке функции;
F – вид функции (может быть или формула, или трёхмерный вектор, задающий каждую координату в параметрической форме, или три отдельные функции, задающие координаты в параметрическом виде);
— x1 – нижняя граница переменной x;
— x2 – верхняя граница переменной x;
— y1 – нижняя граница переменной y;
— y2 – верхняя граница переменной y;
— xgrid – количество точек переменной х;
— ygrid – количество точек переменной y.
В одной системе координат можно построить несколько поверхностей, для этого достаточно определить их, а затем в шаблон графика ввести их имена без аргументов через запятую:
Построение одного и того же графика в декартовой, цилиндрической
и сферической системах координат
Пусть задана какая-нибудь функция, например z(x,y)=const. В различных системах координат эта функция имеет различные графики. В декартовой системе координат это плоскость, параллельная плоскости Оху, в цилиндрической – прямой круговой цилиндр с основанием радиуса const, в сферической – шар радиуса const. Для изменения системы координат, надо по шаблону графика щелкнуть правой кнопкой мыши, в появившемся перечне выбрать «Свойства», затем «Данные QuickPlot» и указать нужную систему координат. Пример:
Для построения многогранников в Mathcad есть функция Polyhedron. Её можно использовать двумя способами:
1) по имени, тогда обращение к функции будет Polyhedron(“имя многогранника”);
2) по коду, тогда обращение к функции будет Polyhedron(“#номер многогранника”).
Построение поверхностей вращения.
Для построения поверхностей вращения в Mathcad удобно использовать функцию CreateMesh.
Параметры функции CreateMesh:
— x1, y1,z1 – матрицы значений для каждой координаты;
— 5 – верхняя граница переменной u;
— 0 – нижняя граница переменной v;
— 2π – верхняя граница переменной v;
— 30 – количество линий в сетке графика.
Параметрические уравнения для поворота вокруг оси Ох:
Параметрические уравнения для поворота вокруг оси Oy:
Пример: рассмотрим гиперболу y 2 – x 2 = 1. При вращении этой гиперболы вокруг оси Ох получается однополостный гиперболоид, при вращении вокруг оси Оу – двуполостный гиперболоид. Построим эти поверхности вращения:
Построение пространственных линий.
Линия в пространстве, рассматриваемая как след движущейся точки, представляется системой трёх уравнений: x = x(t); y = y(t); z = z(t), выражающих координаты точки t. Эти уравнения называются параметрическими уравнениями пространственной линии. Для построения пространственных линий в Mathcad существует функция CreateSpace.
Функция CreateSpace относится к категории Vector and matrix (Векторы и матрицы), так как результатом работы функции будет матрица координат. Работает аналогично CreateMesh. Главное отличие в том, что параметрические уравнения должны быть функциями одной переменной, а не двух, как в CreateMesh. Вызов функции: CreateSpace(F, t1, t2, tgrid). Параметры функции:
— F – вектор параметрических уравнений координат;
— t1 – нижняя граница переменной;
— t2 – верхняя граница переменной;
— tgrid – число линий сетки; не обязательный параметр; чем больше этот параметр, тем более гладкая получается линия; если он не достаточно велик, линия получается с изломами.
Maple. Построение поверхностей и пространственных линий.
График поверхности, заданной явной функцией.
График поверхности, заданной неявно.
Пример: построим поверхность Очевидно, что функция задана неявно, поэтому используем алгоритм, описанный выше.
График поверхности, заданной параметрически.
График пространственных кривых.
Пример: построить пространственную кривую, заданную параметрически х = arctg(t),
В Maple также существует возможность построения нескольких графиков одновременно. Для этого необходимо задать каждую поверхность, а затем использовать команду display. Пример:
Для построения поверхностей вращения в Maple есть функция Surface of revolution. Чтобы ей воспользоваться нужно во вкладке «Tools» выбрать раздел «Tutors», затем подраздел «Сalculus – SingleVariablе», функцию «Surface of revolution». В появившемся окне надо ввести функцию, интервал на котором будет произведено построение, выбрать ось вращения и параметры графика. Окно графика появляется при нажатии кнопки «Close».
Пример: построим поверхности, полученные вращением графика функции y=sin x на интервале от 0 до π вокруг оси Ох и Оу. Вызываем функцию Surface of revolution как описано выше. В поле «f(x)» вводим sin(x), указываем границы интервала, в поле Line of Revolution в одном случае выбираем Vertical, в другом Horizontal, нажимаем Сlose.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Построение кривых второго порядка в среде Mathcad
Построение кривых на плоскости, заданных в декартовых координатах в системе Mathcad.
Для построения графиков используются шаблоны. Их можно выбирать двумя способами.
1 Выбор шаблона с помощью подменю График в меню Вставка (рисунок 17)
2. Выбор шаблона с помощью панелей инструментов. Для этого в панели Math необходимо щелкнуть по кнопке Graph (инструменты графиков) (рисунок 18). Затем щелчком по кнопке панели Graph вставить поле графика соответствующего типа (рисунок 19).
Незаполненный шаблон графика представляет собой большой пустой прямоугольник с шаблонами-местами ввода данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика. В них необходимо ввести выражения, задающие координаты точек графика по осям абсцисс и ординат. В общем случае это могут быть функции некоторой переменной x.
Рисунок 18 Рисунок 19
Если график уже построен, то при его выделении появляются крайние места ввода с автоматически введенными числами, которые служат для указания предельных значений абсцисс и ординат, то есть задают масштаб графика. Сначала рекомендуется использовать автоматическое масштабирование, а лишь затем выбирать более походящий масштаб.
Особое внимание при построении графика следует уделить заданию пределов изменения переменной x. Различают упрощенный способ без задания ранжированной переменной, при котором пределы изменения задаются автоматически, и обычный способ с заданием ранжированной переменной. Упрощенный способ был рассмотрен ранее. При обычном способе необходимо ввести саму функцию и интервал её изменения, а лишь затем выбирать шаблон.
Форматирование двухмерных графиков.
Вид графика можно изменять при помощи команд форматирования графиков. Для изменения формата уже построенного графика необходимо его выделить, щелкнув по нему. Выделенный график обводится сплошной линией с маркерами изменения размера.
Затем к выделенному графику можно применить команду Формат из главного меню и выбрать и выбрать в ней подменю график (рисунок 20). При этом появляется диалоговое окно форматирования (рисунок 21).
Это же диалоговое окно появится, если щелкнуть по выделенному графику правой копкой мыши и выбрать в появившемся меню подменю Формат или дважды щелкнуть левой кнопкой мыши по графику.
Рисунок 20
Диалоговое окно форматирования имеет четыре вкладки:
Оси X-Y – задание параметров отображения осей;
Трассировки (Линии) – задание параметров отображения линий графика;
Метки – задание параметров отображения меток (надписей) у осей;
Умолчание – задание параметров по умолчанию.
Все параметры форматирования относятся к выделенному графику и могут при необходимости меняться.
Задание 2. Построить в одной системе координат графики трех функций. Решение задания на рисунке 24.
В пакете Mathcad также возможно построение кривых, заданных в полярных координатах и в параметрической форме. Примеры таких построений приведены на рисунках 28 и 29.