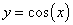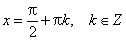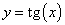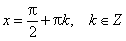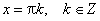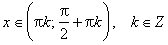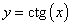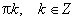Как построить график функции тригонометрия
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Синус и косинус угла на единичной окружности
Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:
С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что
ВС = АВ•sinα = 5•0,8 = 4
Если известно, что cosα = 0,6, то мы сможем найти и второй катет:
АС = АВ•cosα = 5•0,6 = 3
Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:
tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)
Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты хА и уА:
Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:
Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле
Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда
АВ = sinα•ОА = sinα•1 = sinα
С другой стороны, видно, что величина отрезка АВ равна координате уА. Получается, что уА = АВ = sinα, или
Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:
Учитывая, что ОА = 1, а длина ОВ равна координате хА, мы получим следующее:
хА = ОВ = cosα•ОА = cosα•1 = cosα
то есть координата хА равна cos α:
Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.
Таким образом, нам удалось дать новое определение синусу и косинусу угла:
Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть
Тригонометрические функции
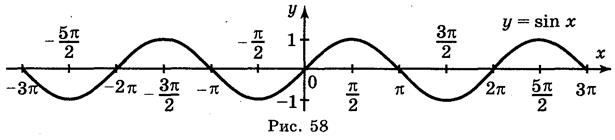
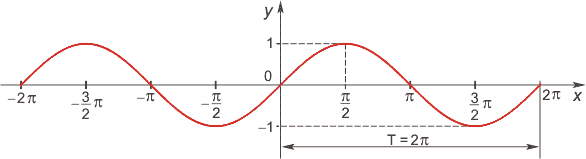
1. Начнем с построения графика функции y = sin x.
Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.
Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть
Это значит, что функция y = sin x является периодической. Мы уже построили уча-сток графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:
Синусоида построена.
Перечислим основные свойства функции y = sin x.
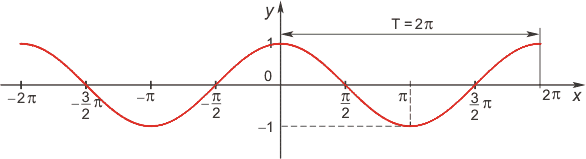
Перечислим основные свойства функции y = cos x.
Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!
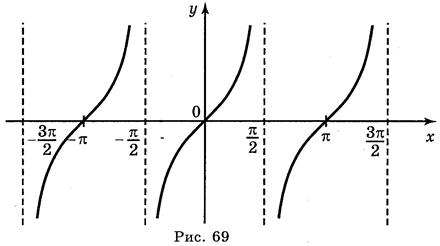
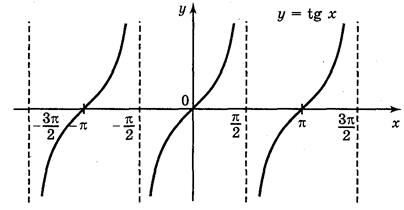
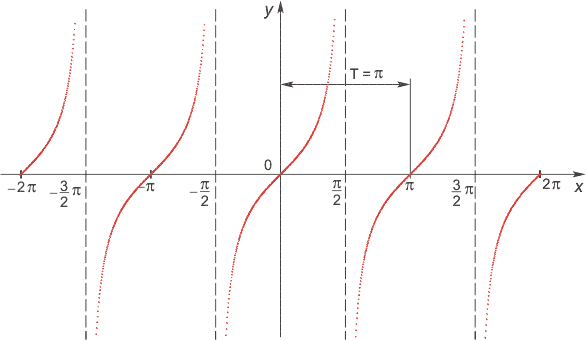
3. Перейдем к графику функции y = tg x.
Осталось только «скопировать» этот участок графика и повторить его с периодом π.
Перечислим свойства функции y = tg x.
5) Функция y = tg x возрастает при то есть на каждом участке, на котором она непрерывна.
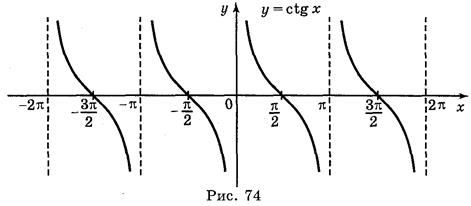
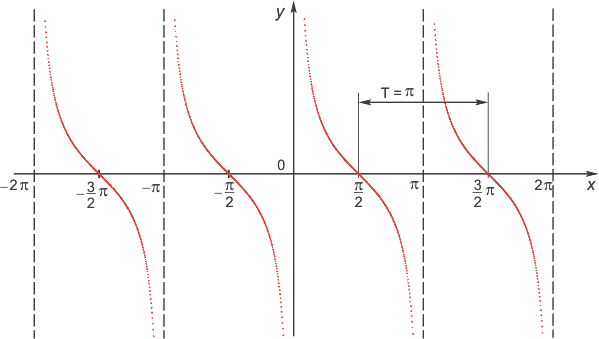
4. График функции y = ctg x строится аналогично. Вот он:
5) Функция y = сtg x убывает при то есть на каждом участке, на котором она непрерывна.
Как построить график функции тригонометрия
Тема. Построение графиков тригонометрических функций
Формирование умений строить графики функций: у = Asin (kx + b ), у = Acos ( kx + b ), у = Atg ( kx + b ), у = Actg ( kx + b ).
И. Проверка домашнего задания
1. Один ученик воспроизводит решение упражнения № 24 (1-3).
2. Фронтальная беседа:
1) Назовите явления в природе, которые периодически повторяются.
2) Дайте определение периодической функции.
4) Найдите наименьший положительный период функций:
a ) y = cos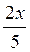 
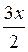
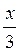
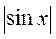
; б) y = sin 
; в) у = tg 
; г) у = 
.
5) периодическая функция у = С? Если да, то укажите период этой функции.
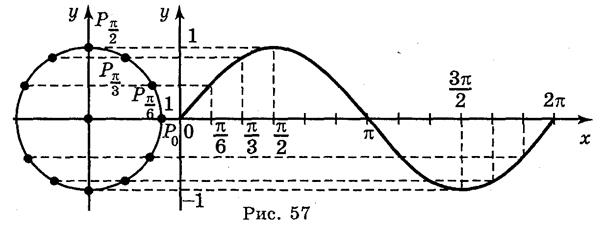
II. Построение графика функции у = sin х
Для построения графика функции у = sin x воспользуемся единичным кругом. Построим единичный круг радиусом 1 см (2 клетки). Справа построим систему координат, как на рис. 57.
На ось ОХ нанесем точки 
; π ; 
; 2 π (соответственно 3 ячейки, 6 ячеек 9 ячеек, 12 ячеек). Разделим первую четверть единичного круга на три равные части и на столько же частей отрезок 
оси абсцисс. Перенесем значение синуса до соответствующих точек оси ОХ. Получим точки, которые надо соединить плавной линией. Затем разделим вторую, третью и четвертую четверть единичного круга также на три равные части и перенесем значение синуса до соответствующей точки оси ОХ. Последовательно соединив все полученные точки, получим график функции у = sin х на промежутке [0;π ].
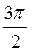
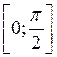
1. Постройте графики функций.
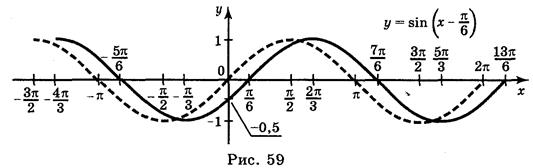
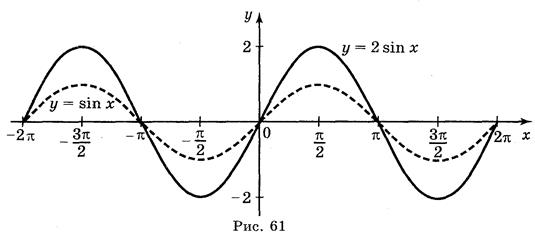
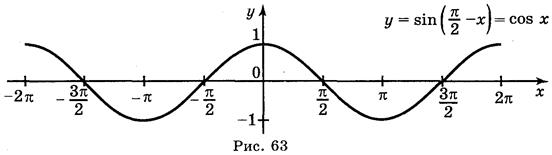
а) у = sin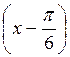 
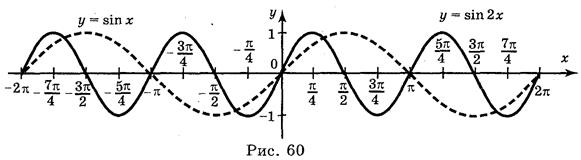
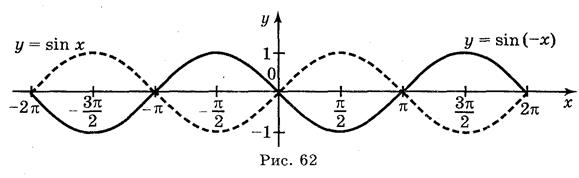
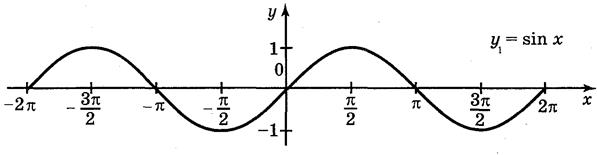
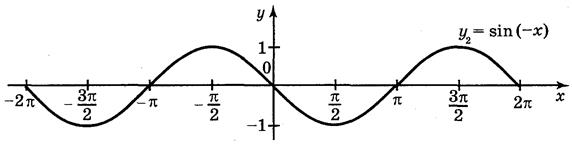
; б) у = sin 2х; в) у = 2 sin х ; г) у = sin (-x).
Ответы: а) рис. 59; б) рис. 60; в) рис. 61; г) рис. 62.
1. Постройте графики функций:
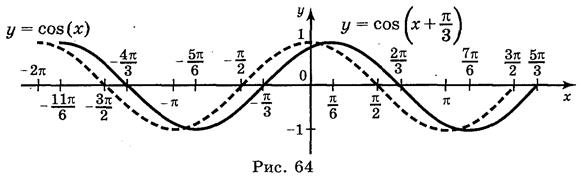
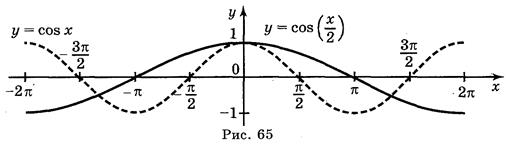
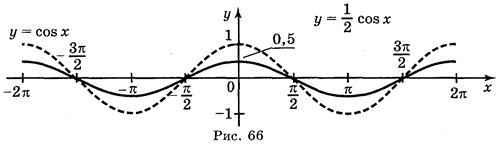
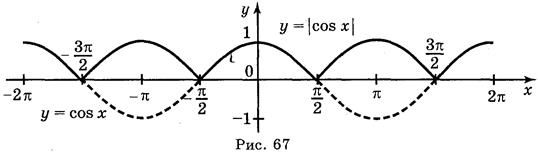
a ) y = cos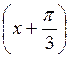 
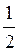
; б) y = cos ; в) y = 
cos х ; г ) у = | cos x |.
Ответ: а) рис. 64; б) рис. 65; в) рис. 66; г) рис. 67.
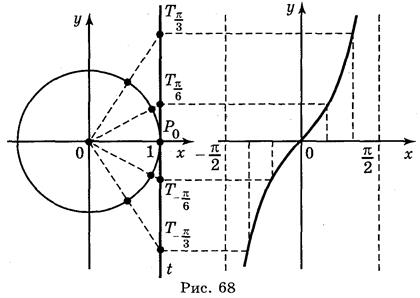
IV. Построение графика функции у = tg x
График функции у = tg x построим с помощью линии тангенсов на промежутке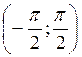 
, длина которого равна периоду π этой функции. Построим единичный круг радиусом 2 см (4 ячейки) и проведем линию тангенсов. Справа построим систему координат, как на рис. 68.
На ось ОХ нанесем точки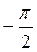 
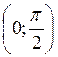
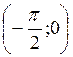
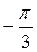
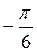
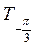
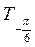
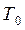
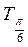
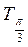
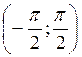
; (6 ячеек). Разделим первую и четвертую четверть окружности на 3 равные части и на столько же частей каждый из отрезков 
и 
. Найдем значения тангенсов чисел 
; 
; 0; 
; 
с помощью линии тангенсов (ординаты точек 
; 
; 
; 
; 
линии тангенсов). Перенесем значения тангенсов до соответствующих точек оси ОХ. Последовательно соединив все полученные точки, получим график функции у = tg x на промежутке .
График функции у = tg x называется тангенсоїдою.
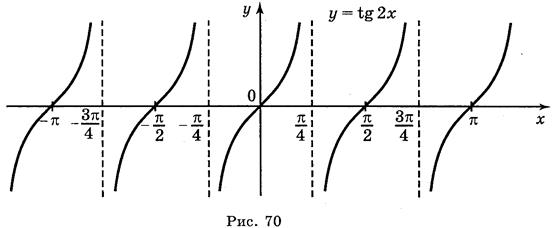
1. Постройте график функций
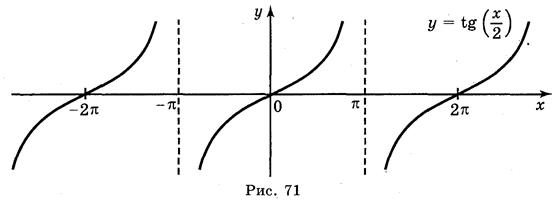
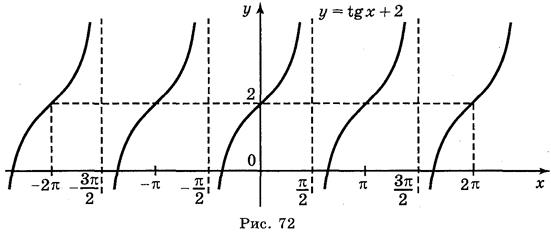
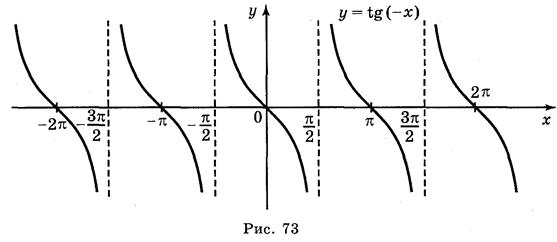
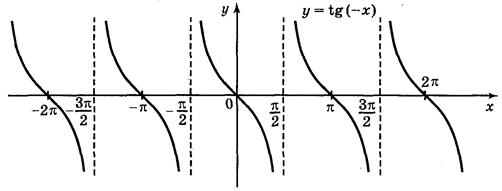
а) у = tg 2х; б) у = t g x ; в) у = tg x + 2; г) у = tg (-x).
Ответы: а) рис. 70; б) рис. 71; в) рис. 72; г) рис. 73.
V. Построение графика функции у = ctg x
График функции у = ctg x легко получить, воспользовавшись формулой ctg x = tg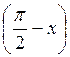 
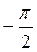
и двумя геометрическими преобразованиями (рис. 74) симметрия относительно оси ΟΥ параллельный перенос вдоль оси ОХ на .
IV. Домашнее задание
Раздел И § 6. Вопросы и задания для повторения раздела И № 50-51. Упражнения № 28 (а-г).
Графики сложных тригонометрических функций
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 20 города Йошкар-Олы»
город Йошкар-Ола, улица Анциферова, дом 29,
Графики сложных тригонометрических
ученица 10А класса
1. Определение синуса, косинуса, тангенса и котангенса.
3. Методы построения графиков сложных тригонометрических функций.
3.1. Построение графиков с помощью компьютерных программ.
3.2. Построение графиков с помощью упрощения формулы. Примеры.
В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в школьном курсе алгебры за 10 класс. Тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций (до применения производной), а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание. Все выше сказанное и обуславливает актуальность выбора темы для данной работы.
Основной целью написания данной работы является представление общих методов построения графиков сложных тригонометрических функций.
• Проанализировать материал учебника “Алгебра и начала математического анализа 10-11”
• Рассмотреть способы и примеры построения графиков сложных геометрических функций
• Предложить одноклассникам творческую работу – составить функцию и построить её график
1. Определение синуса и косинуса
Синус, одна из тригонометрических функций, обозначение sin. Синус острого угла в прямоугольном треугольнике называется отношение катета, лежащего против этого угла, к гипотенузе. Инд. математики синус обозначали словом «джива» (букв. — тетива лука). Арабы переделали этот термин в «джиба», который в дальнейшем превратился в «джайо» — обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus.
Косинус (новолат. cosinus, сокращение от complementi sinus — синус дополнения), одна из тригонометрических функций; обозначение cos. К. острого угла в прямоугольном треугольнике называется отношение катета, прилежащего к этому углу, к гипотенузе.
Тангенс (от лат. tangens — касающийся), одна из тригонометрических функций; обозначение tg. Т. острого угла в прямоугольном треугольнике называется отношение противолежащего катета к катету, прилежащему к этому углу.
Котангенс (новолат. cotangens, сокращение от complementi tangens — тангенс дополнения), одна из тригонометрических функций, обозначение ctg. К. острого угла в прямоугольном треугольнике называется отношение катета, прилежащего к этому углу, к противолежащему катету.
- Синусом α называется отношение AB/OB (отношение противолежащего катета к гипотенузе) Косинусом α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе) Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему) Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему) Секансом α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету) Косекансом α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету)
3.Способы построения графиков сложных тригонометрических функций
3.1. Построение графиков с помощью компьютерных программ.
Построение графика функции в Excel.
Даны функция y = f(x) и отрезок [a, b]. Шаг h=0,1. Построить график этой функции на заданном отрезке, используя табличный процессор.
Пусть f(x) = x • cos(x); a = —10; b = 10.
Для решения задачи воспользуемся ЭТ MS Excel.
Решение состоит из двух шагов:
1) протабулировать заданную функцию на заданном отрезке, т. е. вычислить ее значения с заданным шагом.
Занесем начало и конец отрезка в отдельные ячейки, чтобы при необходимости можно было изменить начало и конец отрезка. В один из столбцов поместим значения аргумента, в другой — значения функции. Ниже приведено начало таблицы в режиме отображения формул.
2) Получив необходимые значения, переходим собственно к построению графика. Для этого воспользуемся мастером диаграмм. Из всех диаграмм наиболее подходящей представляется точечная.
Ниже приведены серия рисунков, иллюстрирующих процесс (шаги) построения графика, и фрагмент таблицы, содержащей конечный результат.
3.2. Построение графиков с помощью упрощения уравнения функции.
При построении графиков функций сложного вида можно примерно придерживаться следующего плана.
1. Найти область определения и область значений функции.
2. Выяснить, является ли функция четной (нечетной).
3. Выяснить, является ли функция периодической.
4. Найти точку пересечения графика функции с осью ординат.
5. Найти нули функции и промежутки знакопостоянства.
6. Вычислить производную функции f(x) и определить точки, в которых могут существовать экстремумы.
7. Найти промежутки монотонности функции.
8. Определить экстремумы функции.
9. Вычислить вторую производную f(x)
10. Определить точки перегиба.
11. Найти промежутки выпуклости функции.
12. Найти асимптоты графика.
13. Найти значения функции в нескольких контрольных точках.
14. Построить эскиз графика функции.
1. y=
y=
=
=
a) Если sin x˃0, то y=2 cos x │sin x│
Как построить график функции тригонометрия
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2 π :
sin(x+2 π· k) = sin x, где k ∈ Z для всех х ∈ R.
| Функция возрастает от −1 до 1 на промежутках: |  |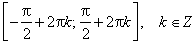
| Функция убывает от −1 до 1 на промежутках: |  |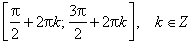
| Наибольшее значение функции sin x = 1 в точках: |  |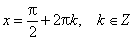
| Наименьшее значение функции sin x = −1 в точках: |  |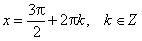
Функция косинус
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2 π :
cos(x+2 π· k) = cos x, где k ∈ Z для всех х ∈ R.
