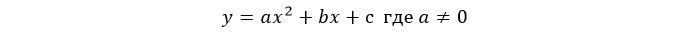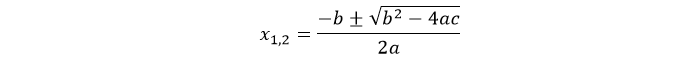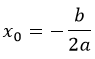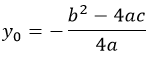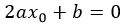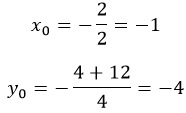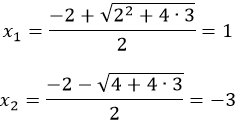Как построить график функции квадратного уравнения
График квадратичной функции (ЕГЭ 2022)
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция.
Проверь себя, ответь на эти вопросы:
Если ты сходу смог ответить, продолжай читать.
Если хоть один вопрос вызвал затруднения, повтори тему «Квадратичная функция».
График квадратичной функции — коротко о главном
Определение
Квадратичная функция – функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
График квадратичной функции – парабола.
Если коэффициент \( \displaystyle a 0\) – ветви параболы направлены вверх.
Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.
Вершина параболы
\( \displaystyle <
Подставляем \( \displaystyle <
\( \displaystyle <
Свободный член \( \displaystyle c\) – это координата пересечения параболы с осью ординат.
Квадратичная функция и её коэффициенты
Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
Ну что же, вот она: \( y=a<
Давай вкратце вспомним, что делают коэффициенты.
С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?
Это вершина. А как найти координаты вершины, помнишь?
Абсцисса ищется по такой формуле:
Вот так: чем больше \( \displaystyle b\), тем левее смещается вершина параболы.
Ординату вершины можно найти, подставив \( <
Подставь сам и посчитай. Что получилось?
Если сделать все правильно и максимально упростить полученное выражение, получится:
Получается, что чем \( \displaystyle b\) больше по модулю, тем выше будет вершина параболы.
Перейдем, наконец, к построению графика.
Самый простой способ – строить параболу, начиная с вершины.
Пример №1
Построить график функции \( y=\frac<1><2><
Решение:
Для начала определим коэффициенты: \( a=\frac<1><2>;\text< >b=2;\text< >c=-1\).
Теперь вычислим координаты вершины:
А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково.
Остается только один вопрос. Как быстро рисовать параболу?
Как быстро рисовать график квадратичной функции — параболу?
Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?
Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить. Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.
Рассмотрим простейшую параболу \( y=<
Закономерность здесь такая.
Если из вершины сместиться вправо (вдоль оси \( \displaystyle Ox\)) на \( \displaystyle 1\), и вверх (вдоль оси \( \displaystyle Oy\)) на \( \displaystyle 1\), то попадем в точку параболы.
Дальше: если из этой точки сместиться вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 3\), снова попадем в точку параболы.
Дальше: вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 5\). Дальше что?
Вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 7\).
И так далее: смещаемся на \( \displaystyle 1\) вправо, и на следующее нечетное число вверх.
То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным \( \displaystyle 1\).
Пример построения параболы быстрым способом
Например, нам стало известно, что вершина параболы находится в точке \( \displaystyle \left( 1;-2 \right)\). Построй (самостоятельно, на бумаге) эту параболу.
Должно получиться так:
Теперь соединяем полученные точки:
ОК, ну что же, теперь строить только параболы с \( \displaystyle a=1\)?
Конечно, нет. Сейчас разберемся, что с ними делать, если \( \displaystyle a\ne 1\).
Три типичных случая построения параболы
Cлучай 1. \( a=-1\).
То есть функция выглядит как \( y=-<
И то же самое, только влево.
Случай 2. \( a>1\).
Что делать, если, например, \( a=2\)?
Все просто: начинаем так же: \( 1\) вправо, но когда дело доходит до «вверх», любое число увеличиваем в \( 2\) раза:
Аналогично в случае \( a
Квадратичная функция (ЕГЭ 2022)
Проверь себя, ответь на эти вопросы:
В конце статьи ты будешь знать ответы на эти вопросы.
Квадратичная функция — коротко о главном
Квадратичная функция – функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
График квадратичной функции – парабола.
Вершина параболы: \( \displaystyle <
Квадратичная функция вида: \( y=a<
Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.
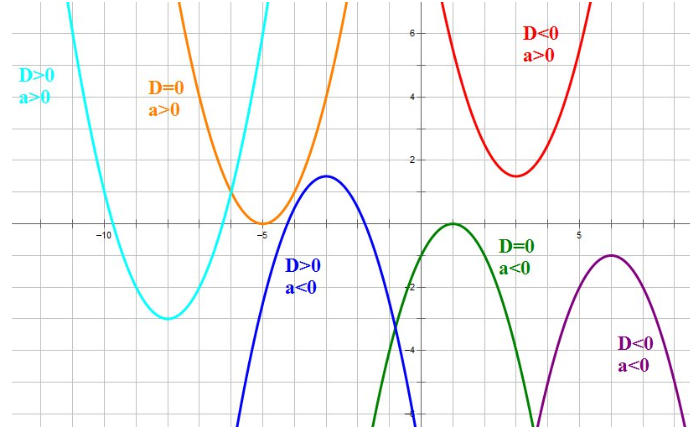
Варианты расположения параболы в зависимости от коэффициента \( \displaystyle a\) и дискриминанта \( \displaystyle D=<^<2>>-4ac\).
Что такое функция?
Не знаешь? Тогда сперва прочитай тему «Функции» – она несложная, но очень важная.
А мы пока повторим.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»? Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции».
Все дело в понятии «область определения»:
Для некоторых функций не все аргументы можно подставить в зависимость.
Например, для функции \( y=\sqrt
Кстати, а с линейной функцией ты уже дружишь? Про нее все написано в теме «Линейная функция» – там ты поймешь, что в функциях ничего страшного нет и научишься понимать и использовать коэффициенты (это циферки перед буквой \( x\)).
И еще, надеюсь, ты умеешь решать квадратные уравнения? Освежить память можно, почитав тему «Квадратные уравнения».
Квадратичная функция — подробнее
Квадратичная функция – это функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (они и называются коэффициентами).
Число \( a\) называют старшим или первым коэффициентом такой функции, \( b\) – вторым коэффициентом, а \( c\) – свободным членом.
Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений\( E\left( y \right)\).
Какими могут быть значения аргумента квадратичной функции \( y=a<
Значит, область определения – все действительные числа:
А теперь множество значений. Все ли значения может принимать функция?
Достаточно рассмотреть самую простую квадратичную функцию \( y=<
\), чтобы убедиться в обратном: ведь какое бы число мы не возводили в квадрат, результат всегда будет больше или равен нулю.
Значит, эта функция всегда не меньше нуля.
А вот больше нуля она может быть сколько угодно: ведь бесконечно большой x в квадрате будет еще больше.
Таким образом, можем написать для \( y=<
В каждом отдельном случае область значений будет разная, но всегда – ограниченная.
График квадратичной функции
Наверняка ты слышал, что график квадратичной функции называется параболой. Как она выглядит? Сейчас нарисуем
Кстати мы очень подробно разобрали как быстро и правильно рисовать параболу. Переходи по ссылке и всему научишься.
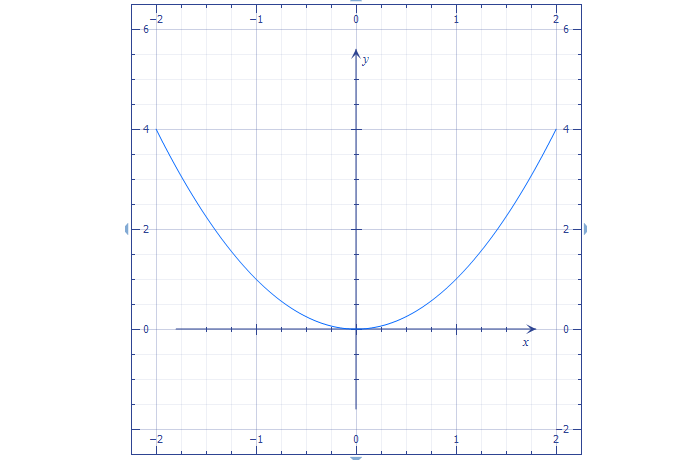
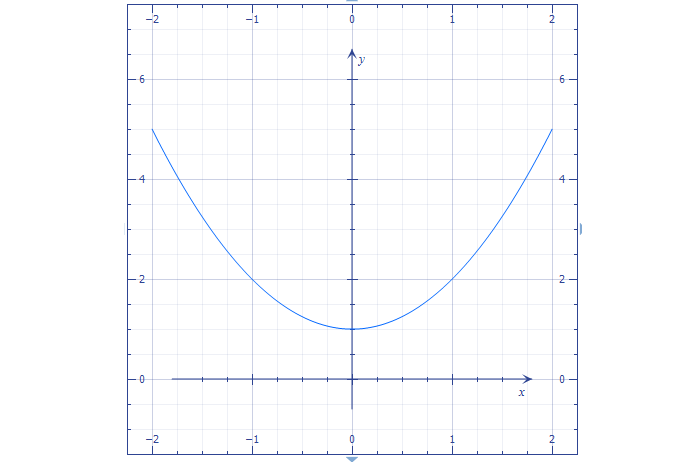
Начнем с простейшей квадратичной функции – \( y=<
Составим таблицу значений:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
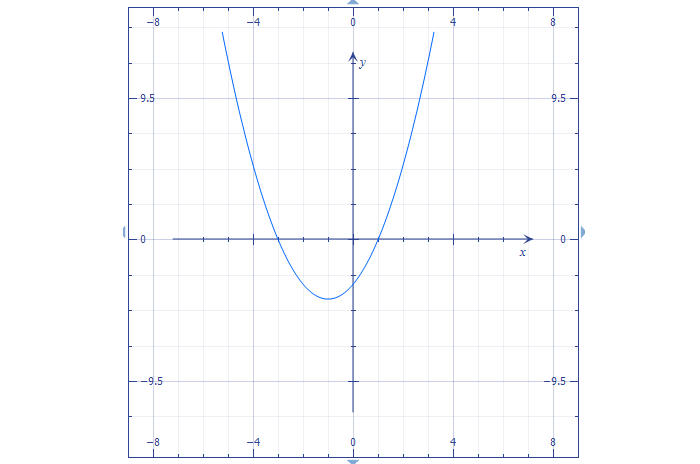
Нарисуем эти точки на координатной плоскости и соединим их плавной линией:
Именно так и выглядит парабола. Самая нижняя ее точка называется вершиной, а части спарва и слева от вершины называем ветвями параболы. Как видим, ветви симметричны относительно вертикали, проходящей через вершину.
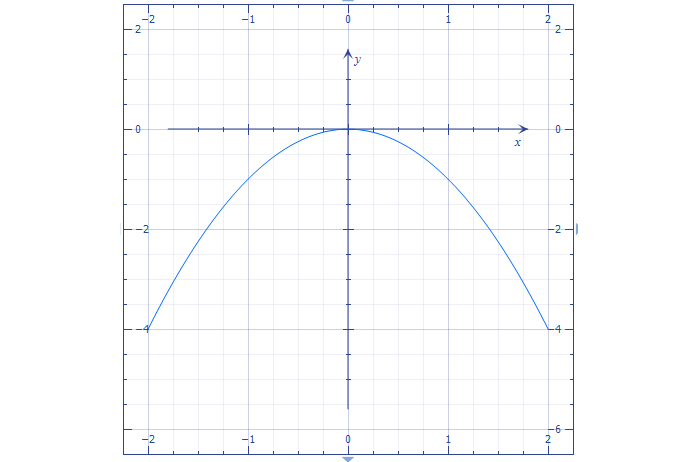
Рассмотрим теперь другую функцию: \( y=<
Составим таблицу значений:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
Сравним два рисунка.
Видно, что это как будто одна и та же парабола, просто расположенная в разных местах.
Во второй параболе вершина переместилась в точку \( \left( 1;-4 \right)\), а ветви переехали вместе с ней.
Да, так оно и есть: все параболы с одинаковым старшим коэффициентом, a выглядят одинаково – даже при разных остальных коэффициентах.
Кстати, если хочешь научиться быстро и правильно рисовать график квадратичной функции, то переходи по ссылке, там отличная статья.
Коэффициенты квадратичной функции
Давай разберем, на что влияют коэффициенты квадратичной функции.
Начнем со старшего коэффициента.
Будем рассматривать функции вида \( y=a<
Что ты видишь? Чем они отличаются? Какую закономерность можно заметить?
Во-первых, это невозможно не заметить, если \( \displaystyle \mathbf \mathbf<0>\) – вверх.
Значит, если парабола пересекает ось \( \displaystyle Ox\) в двух точках, то у нас два корня квадратного уравнения.
Если не пересекает – корней нет.
Но бывает ведь, что дискриминант уравнения равен нулю, и тогда только один корень. В этом случае парабола касается оси \( \displaystyle Ox\) вершиной:
А что такое вершина параболы?
Вершина параболы
Корень уравнения в этом случае указывает на вершину параболы. Если вспомнить формулу корня квадратного уравнения при \( \displaystyle D=0\), получим формулу вершины:
Это тоже бывает очень полезно.
Итак, всего возможны шесть разных вариантов расположения параболы. Вот они все на одном рисунке:
А теперь порешаем задачки.
Решение задач
1. График какой из функций избражен на рисунке?
2. Найдите сумму корней квадратного уравнения \( a<
3. Найдите произведение корней квадратного уравнения \( a<
4. По графику функции \( y=<
Решения
1. Первое: куда «смотрят» ветви параболы? Вниз. А что это значит? Правильно, \( \displaystyle a
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Определение и формула квадратичной функции
Квадратичной называют функцию канонического вида:
Формально конструкция именуется «квадратный трехчлен». Сразу заметно, что область определения не ограничена, а четность не выявлена.
Примеры построения парабол
Займемся упрощенными случаями и подметим закономерности.
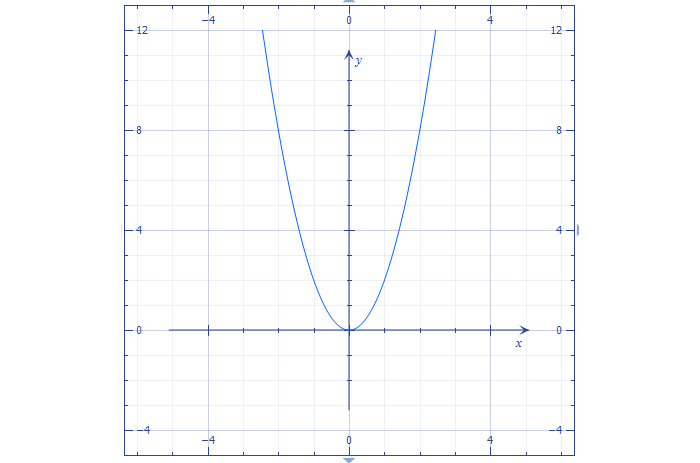
График функции при а = 1, b = c = 0
Наиболее тривиальная, но наглядная и информативная разновидность с формулой:
Функция четная, возрастающая. Построим по точкам.
Получившаяся кривая называется «парабола». Характерна для уравнений с «квадратом».
Нижнюю точку с координатами (0; 0) называют «вершиной». Единственное место, где одной функции соответствует один аргумент. В данном случае – это минимум функции.
Уходящие вверх части кривой – «ветви». На всех участках кроме вершины к одному (y) относятся сразу (±x).
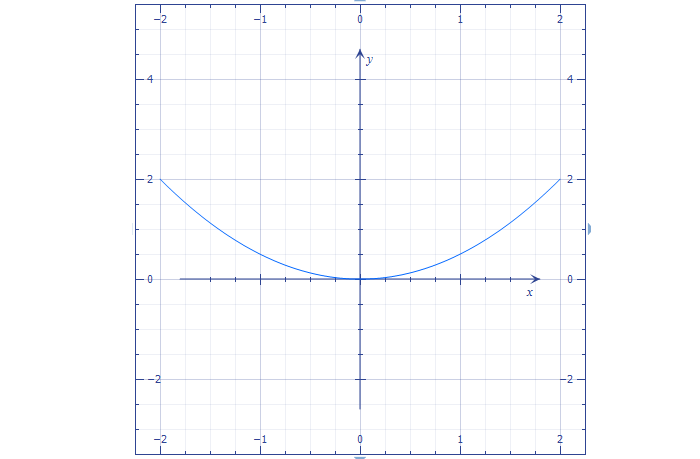
График функции, когда b = c = 0, а > 1 и а y = 2x 2
Ветви «сожмутся» относительно оси симметрии.
Построим другой график.
Куда интереснее переместить коэффициент a в отрицательную область.
Парабола «повернется» на 180°. И вершина станет максимумом.
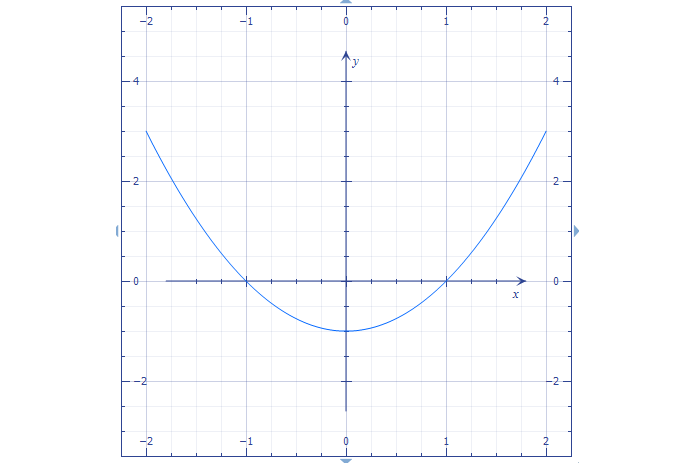
График функции при b = 0, с ≠0
Рассмотрим такой вариант:
Вершина сдвинется на величину c по оси Y.
А если параметр c отрицателен? Уравнение выглядит так:
Смещение произойдет ниже точки (0; 0).
Общий случай a ≠0, b ≠0, c ≠0
Попробуем найти характерные точки.
Пересечения с осью абсцисс (y = 0)
Иными словами, следует решить уравнение:
Корнями уравнения будут:
Подкоренное выражение называется «дискриминант» и обозначается «D». Появляются варианты:
D отрицателен, D > 0. В таком случае действительные корни не существуют. Парабола не пересекает ось Х.
D положителен, D > 0. Существуют оба корня. Кривая пересекает X в двух известных местах.
D = 0. Корень один – -b/2a. Пересечение единственно. А такое возможно в одном случае: найденное означает абсциссу вершины.
Вершина
Горизонтальная координата вычисляется по формуле:
Касательная в вершине параболы совпадает с осью X или параллельна ей. Значит тангенс её относительного наклона равен 0. А это производная функции:
Нашли x0, а y0 находится подстановкой в уравнение найденного.
Ось симметрии
Параллельная оси ординат прямая x = x0.
Приблизительный вид
По уравнению можно прикинуть общую картину:
положительное значение коэффициента a говорит о направленности ветвей вверх и наоборот;
по дискриминанту определим расположение относительно X;
находим пересечения (если есть).
Пример построения графика
a = 1, положительный, поэтому ветви параболы направлены вверх;
Алгоритм построения графика квадратичной функции:
2. Определяем точки пересечения с осью X:
Свойства параболы
Основные свойства следующие:
Область определения – все действительные числа.
Координаты вершины зависят только от коэффициентов.
Ось симметрии проходит через вершину и параллельна оси ординат.
Заключение
В интернете существует масса онлайн-калькуляторов для облегчения работы с кривой. Приведенные же приемы и перечисленные свойства позволяют лучше понять сущность квадратичного выражения.
Параболические отражатели позволяют получать параллельный пучок света от точечного источника. Антенна такого типа позволяет концентрировать и усиливать радиосигнал. Не абстрактная линия на бумаге.
Парабола, график, вершина, нули.
теория по математике 📈 функции
Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax 2 +bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х 2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
D=b 2 – 4ac=4 2 — 4 ∙ 1 ∙ ( − 5 ) = 36
Значит, нули функции равны –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
А) a>0, с >0 Б) а 0 В) а>0, с
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 — это график №1
Б) а 0 — это график №3
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
pазбирался: Даниил Романович | обсудить разбор | оценить