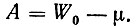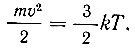Как построить график ферми дирака
Аспирантский реферат. Примеры выполнения
Квантовая статистика Ферми–Дирака описывает идеальный газ из фермионов – ферми–газ.

Из этой формулы следует, что Ф-Д не может быть больше единицы. Это означает, что в одном квантовом состоянии не может находиться более одной ферми–частицы, что согласуется с принципом Паули
Химический потенциал для фермионов может быть только положительным ( μ > 0 ). Иначе при 
Для случая малых чисел заполнения ( Ф-Д тем больше, чем меньше их энергия Е. Что же касается фермионов, то максимальное их число в одном квантовом состоянии не может превышать единицу, что согласуется с принципом Паули.
Химический потенциал μ имеет размерность энергии и в случае фермионов его называют энергией Ферми или уровнем Ферми и обозначают EF. При этом распределение Ферми–Дирака принимает вид
Ф-Д = 
Энергия Ферми является медленно меняющейся функцией температуры Т.
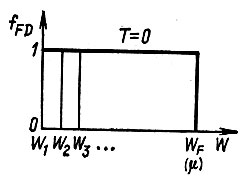
Подставляя в это выражение Т = 0 (говоря о Т = 0, подразумевают, что температура может быть сколь угодно близка к абсолютному нулю, т.е. 
Ф-Д = 1 при E Ф-Д = 0 при E > EF(0)
Здесь ЕF(0) – значение энергии Ферми при Т = 0.
Полученные результаты показывают, что все квантовые состояния с энергиями E EF(0) – свободными.
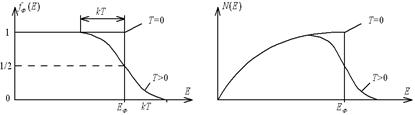
Ниже приведены графики зависимости от Е при Т = 0 (слева) и при Т 
При Т = 0 распределение Ферми–Дирака представляет собой ступенчатую функцию единичной высоты, обрывающуюся при Е = ЕF(0).
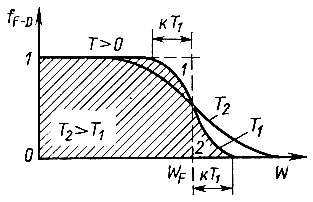
При температуре отличной от нуля резкий скачок Ф-Д от единицы до нуля становится более размытым и происходит в области энергий, ширина которой порядка kT
При любой температуре отличной от нуля 


Это максимальные импульс и скорость, которыми может обладать ферми-частица с массой то при температуре Т = 0.
Функция распределения Ферми-Дирака. Энергия Ферми



Функция распределения для вырожденного коллектива фермионов впервые была получена итальянским физиком Энрико Ферми и английским физиком Полем Дираком:
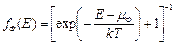
Химический потенциал μ для фермионов обычно называют энергией, или уровнем Ферми – ЕФ.
Анализ выражения показывает, что при Е=ЕФ и температуре Т>0, fФ(Е)=½, т.е. вероятность заселения уровня Ферми при Т>0 равна ½.
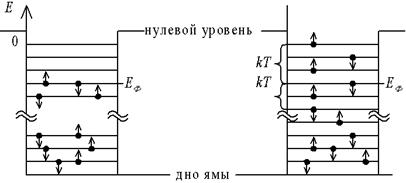
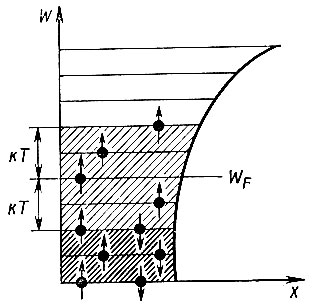
Для того чтобы понять свойства функции Ферми-Дирака, полезно рассмотреть ее поведение при Т=0. Проводник можно представить в виде потенциальной ямы для электронов, выход из которой требует совершения работы по преодолению сил связи, удерживающих электроны – работы выхода (рис. 3.3, а). На рисунке показаны энергетические уровни, которые могут занимать электроны. Согласно постулату Паули, на каждом уровне может располагаться не более двух электронов (с противоположными спинами).
Как видно на рисунке, при Т=0 все уровни ниже уровня Ферми заняты, а все уровни выше этого уровня пусты, т.е. функция fФ(Е) при Т=0 имеет форму ступеньки (рис. 3.4, а).
Рис. 3.4. Распределение Ферми-Дирака: а – функция распределения Ф-Д;
б – полная функция распределения
Таким образом можно определить физический смысл уровня Ферми, но только для проводников. В случае полупроводников или изоляторов это определение неприемлемо, поскольку в этих материалах недостаточно свободных электронов и уровень Ферми находится в запрещенной зоне (п. 4.5).
Умножив функцию распределения (3.20) на число состояний (3.13), получим выражение для полной функции распределения при Т=0 (рис. 3.4, б)
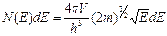
Проинтегрировав (3.21) в указанном интервале энергий, будем иметь выражение для энергии Ферми:
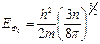
где n – концентрация электронного газа в проводнике.
Используя выражение (3.21), можно получить формулы для вычисления средней энергии – 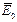
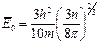
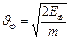
Необходимо отметить, что кинетическая энергия электронов ЕФ не является тепловой энергией, а имеет чисто квантовую природу и определяется свойствами электронов как Ферми-частиц.
С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни (см. рис. 3.3, б). Происходит “размывание” функций распределения (см. рис. 3.4), и ступенька Е=ЕФ преобразуется в интервал, ширина которого равна 2kT. Однако более глубокие состояния электронов остаются неизменными.
Проведенные расчеты показывают, что число термически возбужденных частиц составляет для комнатной температуры всего 1-2% от общего числа. Если проинтегрировать полную функцию распределения во всем энергетическом диапазоне, то можно получить выражение для температурной зависимости энергии Ферми
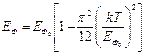
Напомним, что тепловое возбуждение так незначительно влияет на характеристики вырожденного Ферми-газа, что во многих случаях этим влиянием можно пренебречь и считать ЕФ = ЕФо во всем температурном диапазоне.
Можно также вычислить среднюю энергию электронов 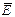
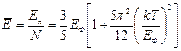
где Еп – полная энергия электронного газа.
Ранее мы говорили о Ферми-газе, считая его вырожденным коллективом. Однако, в случае выполнения критерия (3.11) G>>N, можно говорить о снятии вырождения. Тогда критерий невырожденности (3.11) примет вид
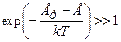
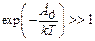
Из последнего соотношения следует, что для невырожденного Ферми-газа должно выполняться условие
При выполнении условия (3.27) единицей в знаменателе выражения (3.20) можно пренебречь, и выражение (3.20) совпадает с формулой для функции Максвелла-Больцмана.
Параметры электронного газа [15]
| Параметры газа | Газ | |
| невырожденный | вырожденный | |
 , Т=0 Т>0 , Т=0 Т>0 | 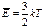 | 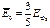 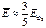 |
| Jкв, Т=0 Т>0 | 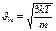 | 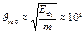 м/с м/с 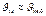 |
| Р, Т=0 Т>0 | 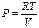 | 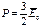 ≈10 10 Па Р ≈ Р0 ≈10 10 Па Р ≈ Р0 |
Из данных таблицы видно, что параметры вырожденного газа в отличие от газа невырожденного при нулевой температуре не равны нулю и практически не зависят от температуры. Это, в свою очередь, говорит о нетепловом квантовомеханическом характере данных процессов.
Как построить график ферми дирака
§ 17. Уровень Ферми в металлах и функция распределения Ферми-Дирака
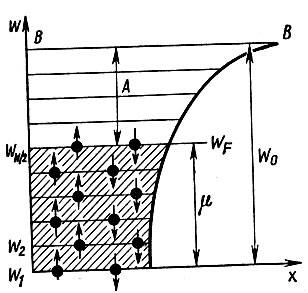
Уровень Ферми. Несмотря на огромное количество свободных электронов в металле, располагаются они по энергетическим уровням потенциальной ямы в строгом порядке. Каждый из электронов занимает вакантное место на возможно более низком уровне. И это вполне естественно, так как всякая система, будучи предоставлена самой себе, то есть в отсутствие внешнего воздействия, всегда стремится перейти в состояние с наименьшей энергией. Распределение электронов по уровням подчинено принципу Паули, согласно которому никакие две частицы не могут находиться в совершенно одинаковых состояниях. В силу этого на каждом энергетическом уровне может расположиться не более двух электронов, да и то имеющих различные направления спинов. По мере укомплектования нижних уровней происходит заселение все более высоко расположенных уровней. Если в рассматриваемом образце металла имеется N свободных электронов, то в отсутствие теплового возбуждения, то есть при абсолютном нуле температуры (T = 0), все свободные электроны разместятся попарно на N/2 нижних уровнях (рис. 47). Самый высокий энергетический уровень потенциальной ямы металла, занятый электронами при Т = 0, называется уровнем Ферми * и обозначается буквой μ или WF. Энергия электрона, находящегося на этом уровне, называется энергией Ферми. Все энергетические уровни, расположенные выше уровня Ферми, при Т = 0 оказываются абсолютно пустыми.
* ( Свое название этот уровень получил в честь выдающегося итальянского физика Э. Ферми, разработавшего совместно с известным английским физиком П. Дираком теорию поведения коллективов частиц, ведущих себя как электроны в металле.)
Рис. 47
Вполне очевидно, что для выхода электронов, находящихся на уровне Ферми, за пределы металла должна быть совершена работа
Рис. 48
Влияние температуры. При температурах, отличных от нуля, вид графика зависимости 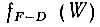
Рис. 49
Рис. 50
Следует отметить, что в диапазоне рабочих температур степень размытия кривой распределения электронов в металле очень невелика. Объясняется это тем, что тепловому возбуждению подвергаются только те электроны, которые расположены на энергетических уровнях, непосредственно примыкающих к уровню Ферми. Можно качественно оценить энергетическую глубину залегания уровней, подвергающихся возбуждению. Из молекулярной физики известно, что кинетическая энергия частиц, обусловленная тепловым движением, выражается так:
Следовательно, значение энергии, которую могут передать электронам испытывающие тепловые колебания атомы кристаллической решетки, по порядку величины равно kT. При комнатной температуре 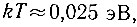
Физический смысл уровня Ферми. Обсуждая в §6 способность твердых тел проводить электрический ток, мы пришли к выводу, что проводимость связана с возможностью перехода электронов на более высокие энергетические уровни, то есть определяется возможностью получения электронами ускорения во внешнем электрическом поле. В металлах при Т > 0 такая возможность имеется только у электронов, находящихся в области размытия функции распределения, так как реальные электрические поля не в состоянии вырвать электроны из глубины потенциальной ямы и перевести их на свободные уровни, энергия которых выше WF (перейти же на соседние, более высоко расположенные уровни глубинные электроны не могут, потому что все эти уровни заняты). Следовательно, при Т > 0 энергия Ферми имеет смысл наиболее вероятной или средней энергии электронов металла, могущих принять участие в проводимости при данной температуре. Эти электроны ответственны не только за создание электрической проводимости. Именно они определяют вклад электронной теплоемкости в общую теплоемкость кристалла и в значительной степени определяют теплопроводность кристалла.
Уровень Ферми в металлах практически не изменяет своего положения по мере повышения температуры. С ростом температуры степень возбуждения электронов растет, и они переходят на более высоко расположенные уровни. Одновременно с этим возбуждению подвергаются и все более глубоко расположенные уровни, имеющие меньшую энергию. Кривая распределения при Т2 > Т1 (см. рис. 50) «размывается» более сильно, чем при T1, но в равной степени вправо и влево. Поэтому средняя энергия электронов, принимающих участие в проводимости, остается практически неизменной. Это тем более справедливо, что между возбужденными уровнями идет постоянный обмен электронами.
Статистика Ферми – Дирака
Распределение частиц по энергии
Приведенное выше распределение Ферми – Дирака дает распределение идентичных фермионов по одночастичным энергетическим состояниям, в которых не более одного фермиона может занимать состояние. Используя распределение F – D, можно найти распределение одинаковых фермионов по энергиям, при котором более одного фермиона могут иметь одинаковую энергию. [nb 2]
Среднее количество фермионов с энергией ε я <\ Displaystyle \ varepsilon _ <я>> 



Распределение Ферми – Дирака приближается к распределению Максвелла – Больцмана в пределе высокой температуры и низкой плотности частиц без необходимости каких-либо специальных предположений:
Для случая электронов проводимости в типичном металле при Т = 300 К (т.е. примерно комнатной температуре) система далека от классического режима, потому что р ¯ ≈ λ ¯ / 25 <\ displaystyle <\ bar 

Большой канонический ансамбль
Из-за качества невзаимодействия каждый доступный одночастичный уровень (с уровнем энергии ϵ ) образует отдельную термодинамическую систему, контактирующую с резервуаром. Другими словами, каждый одночастичный уровень представляет собой отдельный крошечный большой канонический ансамбль. Согласно принципу исключения Паули, существует только два возможных микросостояния для одночастичного уровня: отсутствие частицы (энергия E = 0) или одна частица (энергия E = ε ). Таким образом, результирующая статистическая сумма для этого одночастичного уровня состоит всего из двух членов:
и среднее число частиц для этого подсостояния одночастичного уровня дается выражением
Этот результат применим для каждого одночастичного уровня и, таким образом, дает распределение Ферми – Дирака для всего состояния системы. [22]
Также можно вычислить дисперсию числа частиц (из-за тепловых флуктуаций ) (число частиц имеет простое распределение Бернулли ):
Канонический ансамбль
п ¯ я знак равно ∑ р п я п р <\ displaystyle <\ bar
и уравнение для п ¯ я <\ displaystyle <\ bar 
так что предыдущее выражение для п ¯ я <\ displaystyle <\ bar 

Подобно распределению Максвелла-Больцмана и распределение Бозе-Эйнштейна распределение Ферми-Дирака также может быть получена с помощью метода Дарвина-Фаулера средних значений (см Мюллер-Кирстен [28] ).
Микроканонический ансамбль
Количество способов распределения n i неотличимых частиц по подуровням g i уровня энергии, с максимумом одной частицы на подуровень, задается биномиальным коэффициентом с использованием его комбинаторной интерпретации
Например, распределение двух частиц по трем подуровням даст численность населения 110, 101 или 011, что в сумме составит три способа, что равно 3! / (2! 1!).
ФЕРМИ—ДИРАКА РАСПРЕДЕЛЕНИЕ
Смотреть что такое «ФЕРМИ—ДИРАКА РАСПРЕДЕЛЕНИЕ» в других словарях:
ФЕРМИ-ДИРАКА РАСПРЕДЕЛЕНИЕ — (ферми распре деление) ф ция распределения по уровням энергии тождественных частиц с полуцелым спином при условии, что взаимодействием частиц между собой можно пренебречь. Ф. Д. р. ф ция распределения идеального квантового газа ( ферми газа),… … Физическая энциклопедия
Распределение Ферми — Дирака — как функция от ε/μ, построенная для 4 различных температур. С ростом температуры ступенька размывается Статистика Ферми Дирака в статистической физике квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с… … Википедия
Ферми-Дирака статистика — Распределение Ферми Дирака как функция от ε/μ, построенная для 4 различных температур. С ростом температуры ступенька размывается Статистика Ферми Дирака в статистической физике квантовая статистика, применяемая к системам тождественных фермионов … Википедия
ФЕРМИ-ДИРАКА СТАТИСТИКА — (ферми статистика) квантовая статистика, применяемая к системам тождественных частиц с полуцелым (в единицах h )спином. Такие частицы наз. ферми частицами или фермионами. К ним относятся, напр., электроны, нуклоны, ядра с нечётным числом нуклонов … Физическая энциклопедия
распределение Ферми-Дирака — Fermio skirstinys statusas T sritis radioelektronika atitikmenys: angl. Fermi distribution vok. Fermi Dirac Verteilung, f rus. распределение Ферми, n; распределение Ферми Дирака, n pranc. distribution de Fermi, f; distribution de Fermi Dirac, f … Radioelektronikos terminų žodynas
распределение Ферми-Дирака — Fermio ir Dirako pasiskirstymas statusas T sritis fizika atitikmenys: angl. Fermi Dirac distribution vok. Fermi Dirac Verteilung, f rus. распределение Ферми Дирака, n pranc. distribution de Fermi Dirac, f … Fizikos terminų žodynas
Конденсат Ферми-Дирака — Распределение Ферми Дирака как функция от ε/μ, построенная для 4 различных температур. С ростом температуры ступенька размывается Статистика Ферми Дирака в статистической физике квантовая статистика, применяемая к системам тождественных фермионов … Википедия
Статистика Ферми — Дирака — Статистическая физика Термодинамика Молекулярно кинетическая теория Статистики … Википедия
ФЕРМИ-РАСПРЕДЕЛЕНИЕ — то же, что Ферми Дирака распределение (см. также Ферми Дирака статистика). Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия