Как построить фронтальную проекцию треугольника

Методические рекомендации

Выполнению графических работ должно предшествовать изучение учебной литературы. Необходимо так же изучить символы и обозначения графических элементов (точек, прямых, плоскостей, поверхностей), применяемые при оформлении чертежей.

Основные обозначения и символы

Обозначение	Содержание
	Горизонтальная плоскость проекции
	Фронтальная плоскость проекции
	Профильная плоскость проекции
x	Ось проекции (ось абсцисс)
y	Ось проекции (ось ординат)
z	Ось проекции (ось аппликат)
A, B, C, D…	Точка в пространстве
1,2,3,4,…	Точка в пространстве
A1, B1, C1, 11, 21 …	Горизонтальные проекции точек
A2, B2, C2,12,22…	Фронтальные проекции точек
A3, B 3, C3, 13, 23, 33…	Профильные проекции точек
a, b, c…	Линии в пространстве
a1, b1, c1…	Горизонтальные проекции линий
a2, b2, c2…	Фронтальные проекции линий
a3, b3, c3…	Профильные проекции линий
	Плоскости в пространстве
	Совпадение
	Принадлежность для точки (А а)

Задача 1.В заданной плоскости построить через точку А горизонталь, чeрез точку В- фронталь.

Горизонталью плоскости называется прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (рис.3)

Фронтальная проекция горизонтали всегда параллельна оси х

Фронталью плоскости называется прямая, лежащая в данной плоскости и параллельная фронтальной плоскости проекций (рис.4)

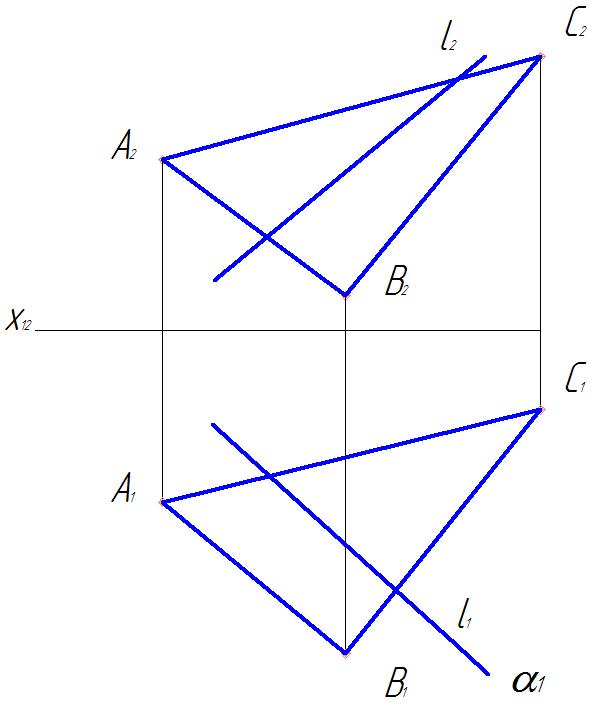
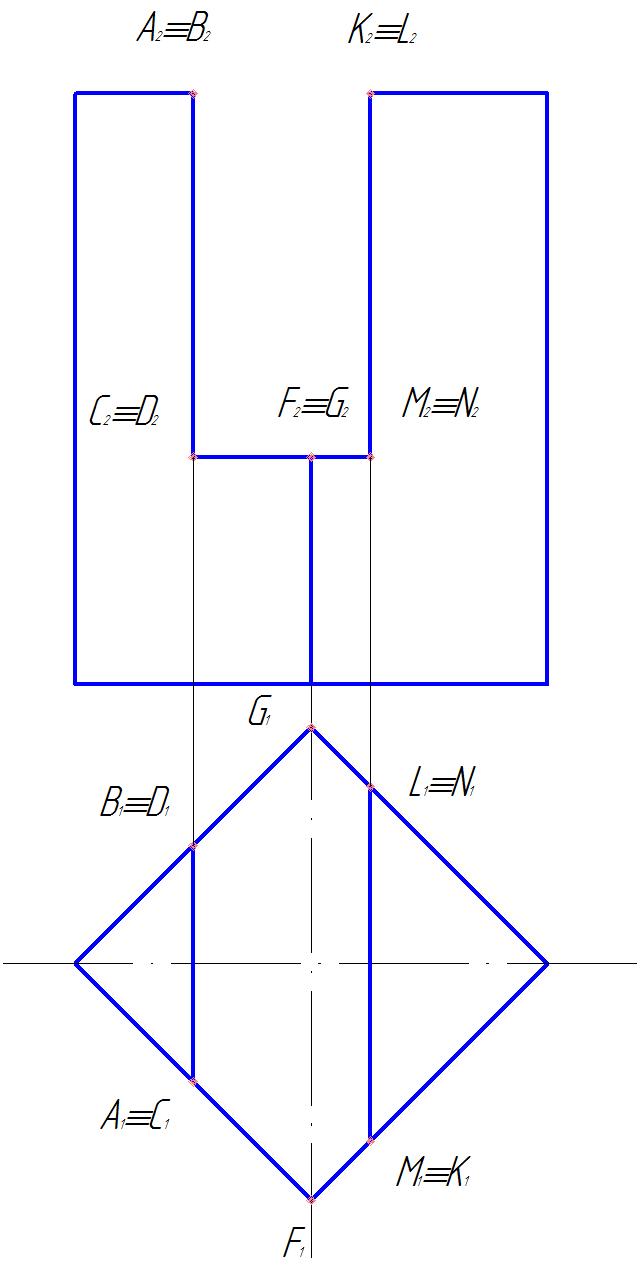
Задача 2.Построить фронтальную (горизонтальную) проекцию треугольника АВС, принадлежащего плоскости (рис. 5).

Точка принадлежит плоскости, если она лежит на прямой принадлежащей этой плоскости. В качестве прямых, принадлежащих плоскости, удобно воспользоваться главными линиями плоскости – горизонталью (h) или фронталью (f).

Ход решения

1. Построим фронтальную проекцию B₂ . Для этого через горизонтальную проекцию B₁ проведем горизонтальную проекцию фронтали параллельно оси х, построим ее фронтальную проекцию параллельно f₂ и отметим на ней фронтальную проекцию B₂.

2. Аналогично строим фронтальную проекцию C₂.

3. Построим фронтальную проекцию точки А₂. Если горизонтальная проекция точки А₁ принадлежит горизонтальной проекции прямой h₁, то фронтальная проекция А₂ находится на h₂ (рис. 6).

4. Соединим А₂В₂С₂ и получим недостающую фронтальную проекцию треугольника АВС (рис.7).

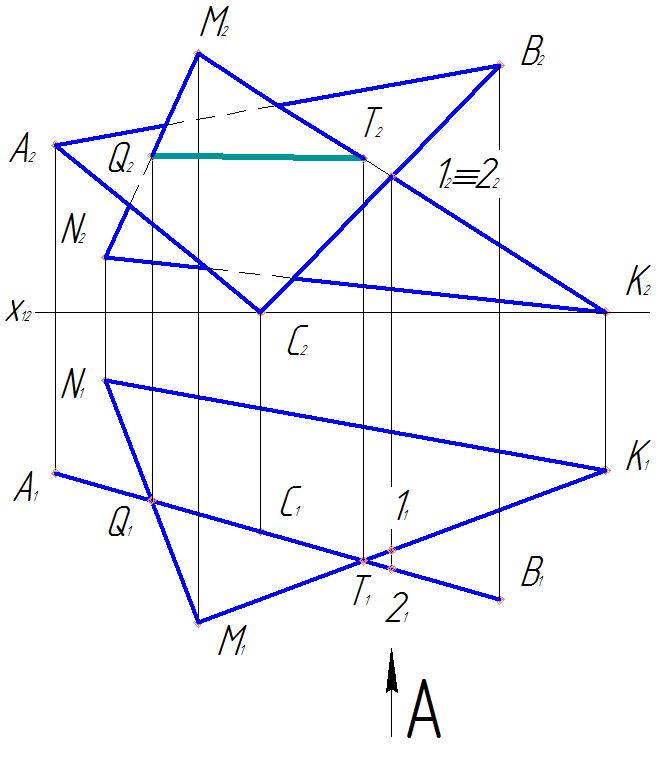
Задача 3. Построить линию пересечения плоскостей (рис. 8)

Плоскость ΔАВС частного положения (ΔАВС π₁), плоскость ΔMNK – общего положения

Две плоскости пересекаются по прямой. Чтобы построить эту прямую, надо найти две общие точки для этих плоскостей.

1. Отметим общие горизонтальные проекции Q₁ и T₁ на пересечении горизонтальных проекций треугольников АВС и MNK (рис.9).

2. Фронтальные проекции Q₂ и T₂ ищем на линиях проекционной связи в ΔM₂N₂K₂.

4. Определим видимость плоских фигур, т.к. плоскости считаются непрозрачными. Видимость горизонтальной проекции фигур определять не надо, т.к. ΔАВС проецируется в прямую линию, проекция M₁N₁K₁видима. Определим видимость плоских фигур относительно плоскости проекций π₂. Для этого рассмотрим конкурирующие точки 1 и 2, лежащие на скрещивающихся прямых ВС и МK. Фронтальные проекции 1₂ и 2₂ совпадают, а горизонтальная проекция 2₁ находится перед горизонтальной проекцией 1₁. Точка 1₂ не видима относительно плоскости проекций π₂. Далее рассуждаем так: точка 2 лежит на ΔАВС, следовательно, фронтальная проекция ΔА₂В₂С₂ видима на π₂ с той стороны, где находятся точки 1₂ и 2₂. После фронтальной проекции линии пересечения Q₂ и T₂ видимость Δ А₂В₂С₂ меняется на противоположную, т.е. он становится невидимым (рис.9).

Задача 4.Построить линию пересечения плоскостей.(рис.10)

Заданы две плоскости общего положения.

Ход решения

1. Проведем вспомогательную плоскость частного положения, например плоскость горизонтального уровня α ׀׀ π₁ (рис.11).

3. Плоскость α пересечет плоскость (а∩b) по прямой 2-3.

5. Для построения второй общей точки проведем еще одну вспомогательную плоскость β ׀׀ π₁ (рис.12).

6. Плоскость β пересечет плоскость α по горизонтали h_’

7. Плоскость β пересечет плоскость (а∩b) по прямой 5-6.

8. Прямые h_’ ‘и 5-6 пересекутся в точке N(N₁ и N₂). Соединяем одноименные проекции точек М и N получим проекции линии пересечения (М₁N₁) и (М₂N₂).

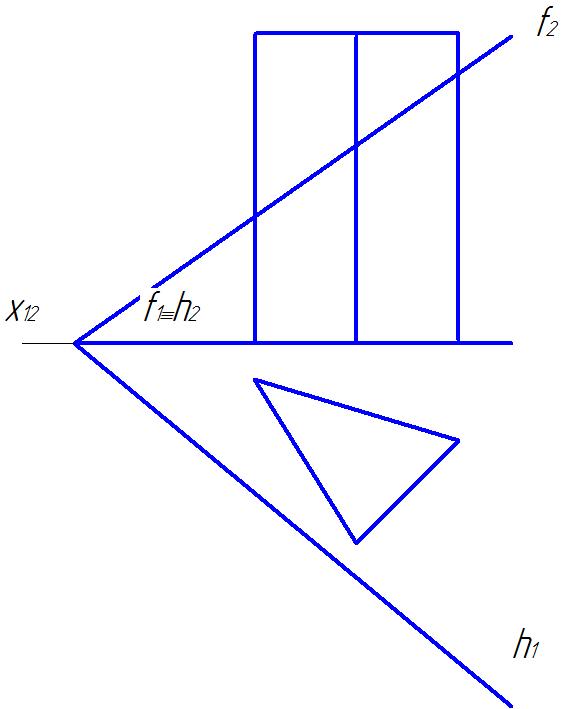
Пример 1. Плоскость задана двумя пересекающимися прямыми h и f (рис.13).

Ход решения

1. Для построения точки пересечения прямой l с плоскостью необходимо через прямую провести вспомогательную плоскость частного положения, например фронтально-проецирующую α π₂, l₂ α₂(рис. 14).

2. Строим линию пересечения 12 заданной и вспомогательной плоскости (рис. 15)

3. Определяем точку пересечения К заданной прямой l с линией пересечения 12.

4. Видимость прямой l в случае задания плоскости следами не определяем.

Пример 2. Плоскость задана плоской фигурой (рис. 16).

Ход решения

1. Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую α 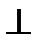π₁. l₁ α₁ (рис. 16).

2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М₁=А₁С₁ ∩ α_1, М₂ А₂С₂ и N₁=В₁С₁∩α _1,N₂ В₂С₂ (рис. 17).

3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К₂= М₂N₂∩l₂. К₁ находится в пересечении линии проекционной связи, проведенной из К₂ и М’N’.

4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.

Определим видимость прямой l относительно плоскость π₁. Отметим горизонтальную проекцию 3₁ совпадающую с горизонтальной проекцией М₁. М₂ А₂С₂ уже отмечена, 3₂ l₂. Фронтальная проекция М лежит выше фронтальной проекции 3₂, следовательно, точка М видима относительно π₁. Точка 3 лежит на l, следовательно от М₁ ≡3 ₁ до К ₁, горизонтальная проекция l ₁ невидима. В горизонтальной проекции К ₁ видимость меняется на противоположную. За границами ΔАВС прямая l везде видима.

Задача 6.Построить линию пересечения плоскости общего положения с заданной поверхностью.

Пример1.Трехгранная призма (рис.18).

Ход решения

Ребра призмы перпендикуляры горизонтальной плоскости проекций, поэтому горизонтальные проекции A₁,В_1,С₁ точек встречи ребер призмы с плоскостью совпадают с горизонтальными проекциями вершин основания призмы. Фронтальные проекции А₂,В₂,С₂ точек А, В, С будут лежать на фронтальных проекциях фронталей плоскости, проведенных через эти точки (рис.19).

Полученные точки соединили с учетом видимости граней призмы (рис.20).

Пример 2. Пересечение цилиндрической поверхности плоскостью общего положения (рис.21).

Прямая круговая цилиндрическая поверхность пересекается плоскостью общего положения. Плоскость задана пересекающимися прямыми m и n. Построить проекции линии пересечения.

Линией пересечения прямой круговой цилиндрической поверхности плоскостью общего положения является эллипс.

Данная цилиндрическая поверхность является горизонтально-проецирующей, так как ее образующие перпендикулярны горизонтальной плоскости проекций. Следовательно, линия пересечения, как принадлежащая такой поверхности, на горизонтальную плоскость проекций проецируется в виде очерка этой поверхности, т.е. в виде окружности. На фронтальную плоскость проекций линия пересечения проецируется в виде эллипса.

Отметим опорные (базовые), обязательные для построения точки, принадлежащие линии пересечения:

— точки, наиболее и наименее удаленные от плоскостей проекций;

— точки перехода от видимой к невидимой части линии пересечения

1.В рассматриваемом примере фигурой сечения является эллипс, имеющий большую и малую ось..

Большая ось принадлежит линии наибольшего ската секущей плоскости, проходящей через ось вращения цилиндрической поверхности и располагающейся перпендикулярно горизонталям секущей плоскости. Для построения большой оси необходимо на горизонтальной проекции через центр основания провести прямую перпендикулярную прямой m, являющейся горизонталью секущей плоскости. Отметить точки М и N пересечения с очерком цилиндрической поверхности, и точку 1 с прямой m. Спроецируем точку 1 на фронтальную проекцию прямой m. Отрезок MN – большая ось эллипса (рис.22)

Малая ось эллипса перпендикулярна большой оси. Взаимная перпендикулярность между осями сохранится только на горизонтальной проекции, так как малая ось, являясь горизонталью секущей плоскости, параллельна горизонтальной плоскости проекций, а большая ось, являясь прямой общего положения. Следовательно, для построения малой оси нужно на горизонтальной проекции через центр эллипса провести прямую перпендикулярно отрезку MN и отметить точки А и В пересечения с очерком цилиндрической поверхности.

Центр эллипса (точка О) на горизонтальной проекции совпадает с центром основания цилиндрической поверхности. Фронтальная проекция точки О является точкой пересечения фронтальных проекций большой и малой оси.

.Наиболее и наименее удаленные от горизонтальной плоскости проекций точки фигуры сечения определяются на фронтальной проекции. Это точки М и N, принадлежащие большой оси эллипса.

2.Наиболее и наименее удаленные от фронтальной плоскости проекций точки определяются на горизонтальной проекции. Это точки E и F – точки пересечения вертикальной оси симметрии с очерком цилиндрической поверхности. Для построения их фронтальной проекции следует использовать горизонтали секущей плоскости(рис.23).

.3. Точками перехода от видимой к невидимой части линии пересечения являются точки, принадлежащие очерковым образующим. На горизонтальной проекции им соответствуют точки пересечения очерка цилиндрической поверхности с горизонтальной осью симметрии – точки C и D. Их перенос на фронтальную проекцию выполняется также с помощью горизонталей секущей плоскости (рис.24).

Для более точного построения проекций линии пересечения следует ввести дополнительные точки. Целесообразно брать точки, принадлежащие тем же горизонталям, которые были использованы для построения опорных точек.

Соединяем с учетом видимости с помощью лекала полученные точки.

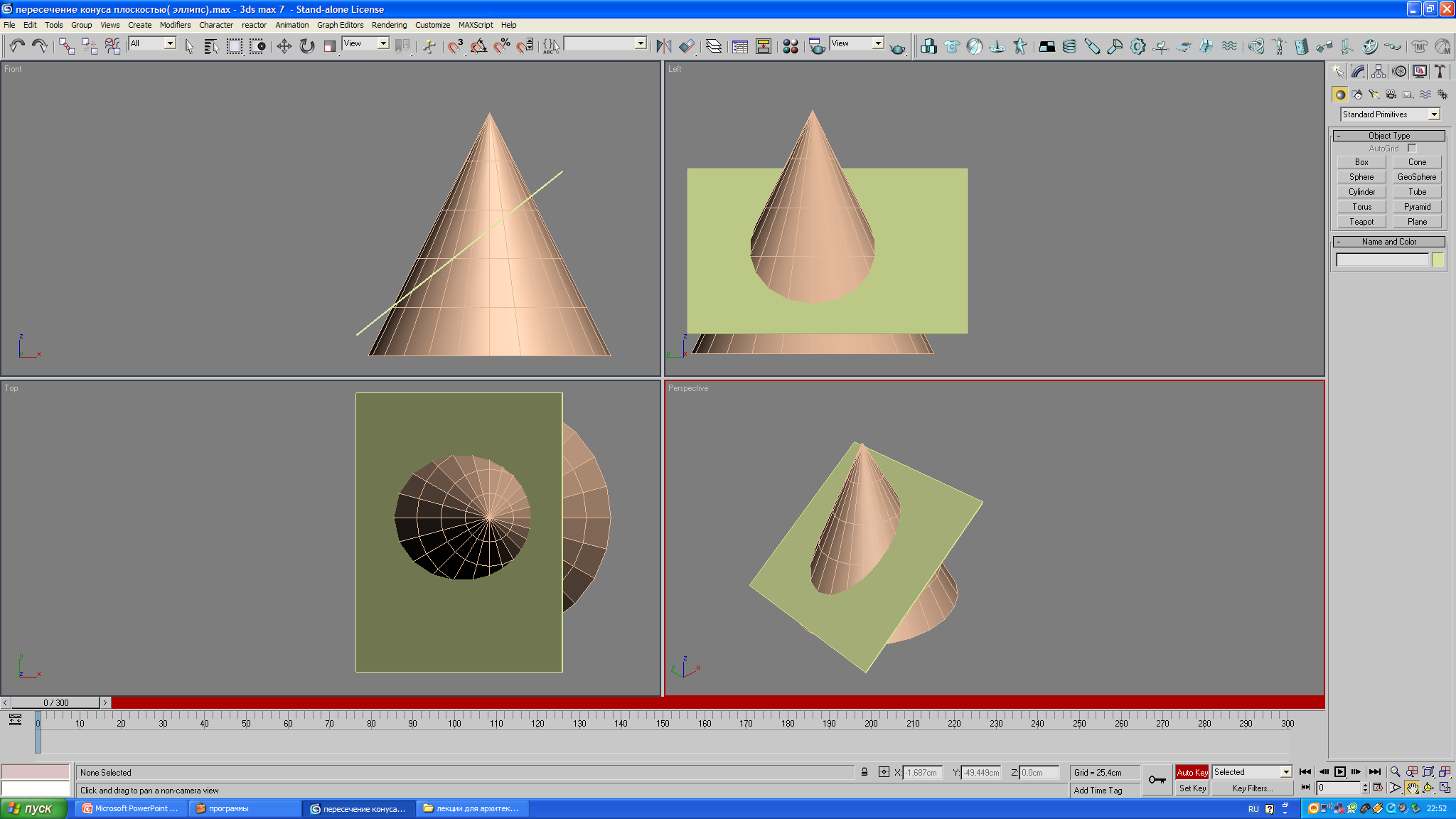
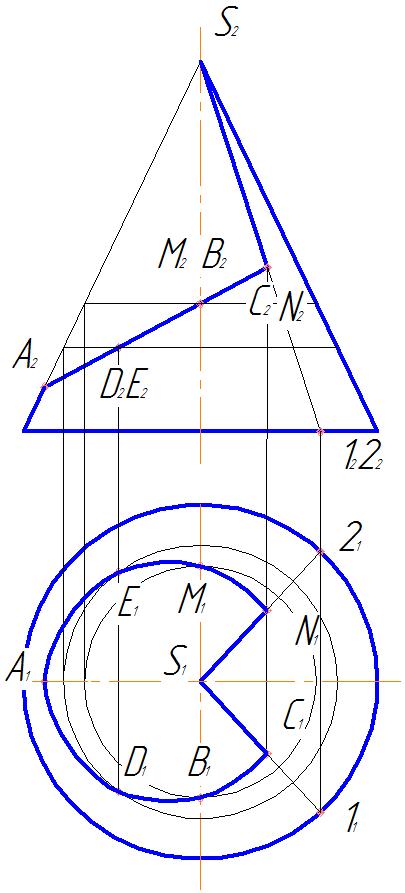
Задача 7.Построить линию пересечения поверхности конуса с плоскостью (рис. 25).

Задан конус и плоскость частного положения, в данной задаче плоскость фронтально-проецирующая α π₂. Линия пересечения поверхности конуса с фронтально-проецирующей плоскостью представляет собой эллипс. Эллипс – это лекальная кривая, которая строится минимум по 8 точкам. Фронтальная проекция эллипса совпадает с фронтальной проекцией плоскости α.

Ход решения

2. Для получения горизонтальных проекций C ₁ и D ₁ проведем параллельно основанию линию, горизонтальная проекция которой является окружностью, и на ней отметим C₁ и D₁.

4. Полученные горизонтальные проекции точек надо соединить плавной кривой от руки, а затем обвести по лекалу (рис. 27).

Пример 1. Конус (рис. 28).

Ход решения

1. Заключаем прямую l в плоскость частного положения так, чтобы при пересечении конуса с плоскостью была простая линия пересечения – окружность. В данной задаче α – горизонтальная плоскость, l₂ α₂.

(рис. 29).

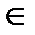
2. Строим линию пересечения конуса с плоскостью α. Это окружность радиуса R.

4. Определяем видимость прямой l. Между получившимися точками M и N прямая всегда невидима. Горизонтальная проекция прямая l₁ видима (невидима только от M₁ до N₁). Фронтальная проекция l₂ до М₂ видима, т.к. точка М лежит на видимой части конуса относительно π₂. Точка N лежит на невидимой части конуса относительно π₂, следовательно, фронтальная проекция l₂ от N₂ до очерковой образующей невидима. За очертаниями конуса прямая l всегда видима (рис.30 ).2

Ход решения

1. Заключаем прямую l во вспомогательную плоскость частного положения. Линией пересечения плоскости с гранной поверхностью будет ломаная линия. Заключаем прямую l во фронтально-проецирующую плоскость α^π₂, l₂Î α₂ (рис. 32).

2. Строим линию пересечения плоскости α с призмой. Отметим 1₂, 2₂, 3₂ на α₂.

3. Построим горизонтальные проекции 1₁, 2₁ и 3₁ на соответствующих ребрах.

4. Соединяем горизонтальные проекции1₁-2₁-3₁ломаной линией с учетом видимости.

5. На пересечении горизонтальной проекции l₁ с горизонтальной проекцией 1₁-2₁-3₁ отметим горизонтальные проекции M₁ и N₁искомых точек М и N.

7. Определяем видимость прямой l. Между полученными точками M и N прямая невидима всегда. Горизонтальная проекция l₁ невидима между M₁N₁ и от M₁ до горизонтальной проекции ребра В₁, т. к. горизонтальная проекция М₁ принадлежит невидимой относительно π₁ грани ВС.

На π₂: точка М лежит на грани BС видимой относительно π₂, следовательно, М₂ видима и фронтальная проекция l₂ видима до М₂. Точка N принадлежит грани А C, невидимой относительно π₂, следовательно, фронтальная проекция N₂ не видима и фронтальная проекция l₂ от N₂ невидима. За очертаниями призмы прямая l видима (рис. 33).

Задача 9.Построить три проекции геометрического тела с вырезом. Выполнить задачу 9 на формате А3.

Пример 1. Вырез на конусе (рис. 34).

Вырез произведен двумя плоскостями. Одна проходит через вершину конуса и рассечет его поверхность по образующим. Вторая плоскость – фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей.

Ход решения

1. Отметим фронтальные проекции характерных точек для построения выреза – А₂, В₂, С₂, M₂, N₂ (рис. 35).

2. Точки D и Е выбраны произвольно для построения эллипса, т.к. линия среза от А до С N представляет собой часть эллипса.

3. Найдем горизонтальные проекции точек А, В, С, D, Е, N. Точки лежат на поверхности конуса, а значит, они лежат линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E найдены на окружностях, принадлежащих поверхности конуса. Точки С и N – на образующих S1 и S2.

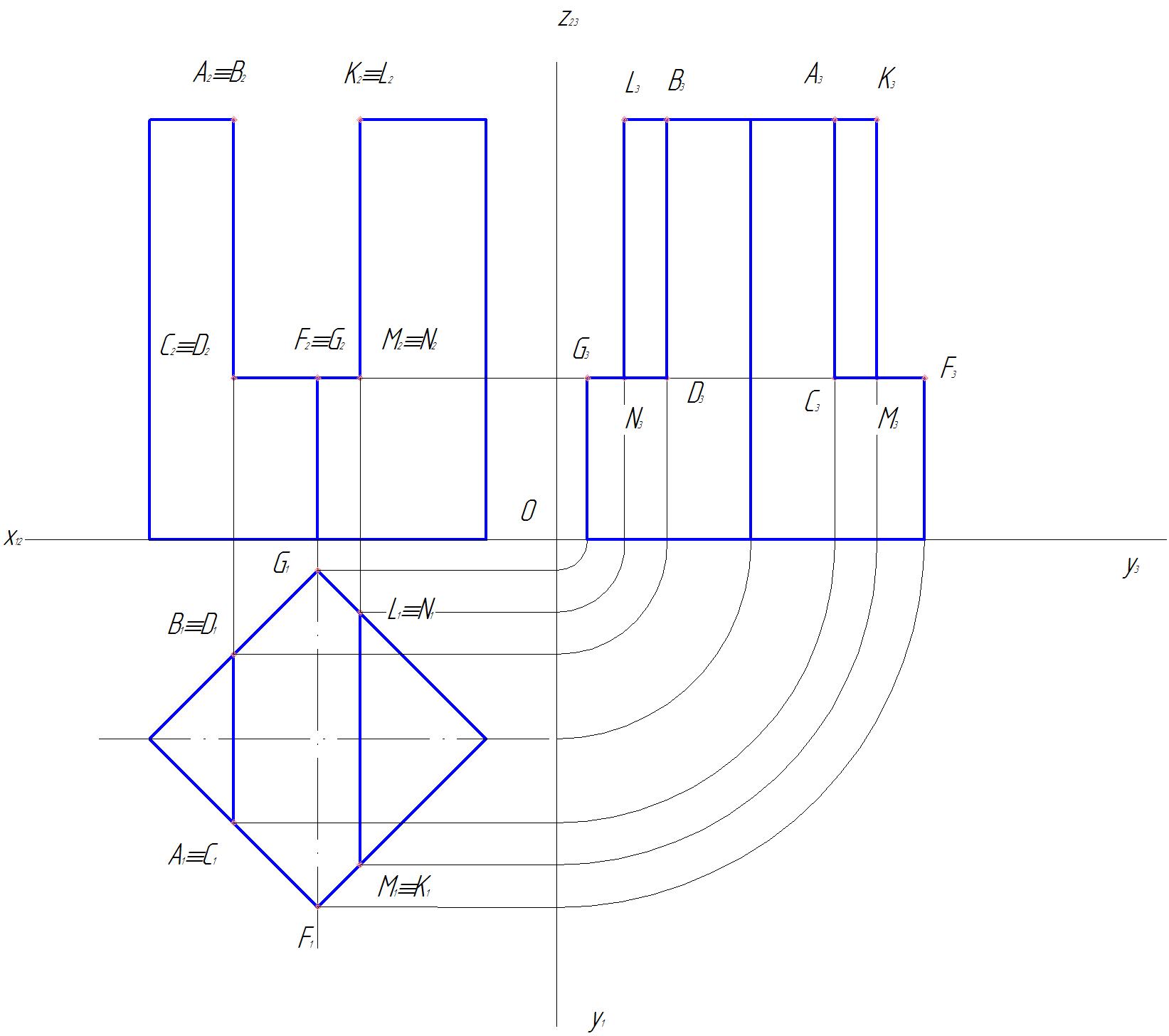
5. Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис. 37)

Пример 2. Вырез на цилиндре (рис. 38).

Вырез произведен тремя плоскостями. Наклонные фронтально-проецирующие плоскости рассекут цилиндр по части эллипса, ограниченного прямой. Плоскость, параллельная оси вращения пересекает поверхность цилиндра по образующим.

Ход решения

1.Отметим на фронтальной проекции выреза фронтальные проекции A₂,F₂,G₂,K₂,L₂,P₂. Характерные точки D₂, E₂, M₂, N₂ – на оси симметрии цилиндра, B₂, C₂, T₂,V₂ – отмечены произвольно на линии, принадлежащей поверхности цилиндра. Все точки принадлежат боковой поверхности цилиндра, которая проецируется в окружность на горизонтальной плоскости проекций. Поэтому все горизонтальные проекции точек принадлежат этой окружности (рис. 39).

2. Найдем профильные проекции всех точек. Затем полученные точки соединяем. Линия GECABDF – часть эллипса, FK и GL – отрезки прямых, GF и KL – отрезки прямых, LNVPTMK – часть эллипса (рис.40 ).

Пример3. Вырез на призме(рис.41)

Пример4.Вырез на пирамиде (рис. 42).

Пример5.Вырез на сфере (рис. 43).

Задача 10. Построить линию пересечения поверхностей геометрических тел.

Пример 1. Пересечение сферы с цилиндром. Цилиндр занимает фронтально-проецирующее положение (рис.44 ).

Ход решения

2. Соединим полученные точки плавной линией с учетом видимости. Точки, принадлежащие видимой части поверхности цилиндра относительно горизонтальной плоскости проекций соединяем сплошной линией. В точках М,N,K,L происходит изменение видимости. Определим видимость горизонтальных очерков цилиндра и сферы (рис. 46).

Пример 2. Пересечение сферы с конусом (рис. 47).

Обе поверхности общего вида. У этих поверхностей имеется общая плоскость симметрии, поэтому линия пересечения будет симметрична относительно этой плоскости. Обе поверхности второго порядка, следовательно, линия их пересечения пространственная кривая четвертого порядка.

Ход решения

1. Отметим характерные точки линии пересечения. Точки А и В лежат на пересечении фронтальных очерков. Точки С и D найдем на пересечении экватора сферы a и окружности b поверхности конуса, лежащих в одной горизонтальной плоскости α. Аналогично могут быть найдены и другие точки линии пересечения. Так точки М и N строим как пересечение окружностей c и d, принадлежащих одной горизонтальной плоскости β (рис.47).

3. Полученные точки соединяем плавной кривой с учетом видимости. При установлении видимости следует помнить, что эта линия будет видима, если она принадлежит как поверхности сферы, так и конуса. Точки А и В отделяют видимую относительно фронтальной плоскости часть линии пересечения (она проходит через точки А, С, М, В) от невидимой. В данной задаче фронтальные проекции видимой и невидимой части линии пересечения совпадают.

Точки С и D отделяют видимую относительно горизонтальной плоскости часть линии пересечения от невидимой. Точка А видима относительно горизонтальной плоскости проекций, так как лежит выше экватора сферы. Следовательно линия, проходящая через точки А, С, D – видима, остальная часть линии невидима. Определим видимость очерков поверхности конуса и сферы (рис. 48).

Задача 11.Определить расстояния от точки А до прямой l (рис. 49)

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.

Ход решения

1. На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Поэтому сначала строим дополнительную ортогональную проекцию прямой и точки А на плоскости π₄, параллельной прямой l и перпендикулярной к π₁. При этом ось х₁₄ параллельна l_1. Для построения дополнительной проекции прямой l на ней отмечены точки 1 и 2 (рис. 50).

2. Проводим дополнительную проекцию А₄K₄ перпендикуляра (А₄K₄ l₄), а затем строим горизонтальную проекцию А₁К₁. Построена также и фронтальная А₂К₂ проекция перпендикуляра АК.

3. По двум данным проекциям отрезка АК (А₁К₁ и А₄K₄) находим его длину, построив дополнительную ортогональную проекцию отрезка на плоскости π₅, параллельной АК и перпендикулярной к π₄ (рис. 51).

Аналогично можно определить расстояние между двумя параллельными прямыми.

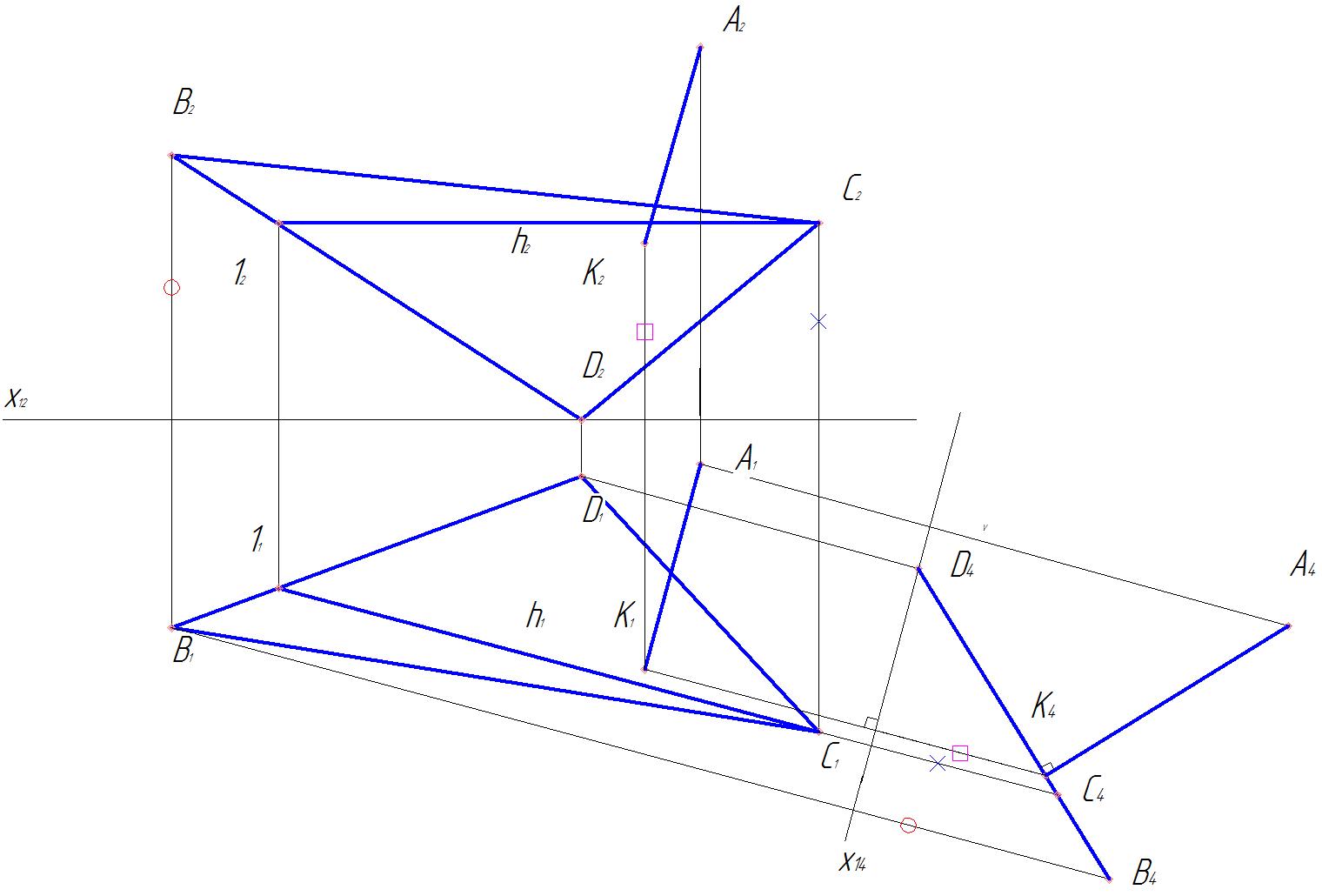
Задача 12.Определить расстояние от точки А до плоскости α(ΔВСD) (рис.52

Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.

Если плоскость является проецирующей, то перпендикуляр к ней параллелен плоскости проекций и длина проекции его отрезка на этой плоскости проекций равна искомому расстоянию. Исходя из этого построим дополнительную ортогональную проекцию плоскости α и точки А на плоскости π₄, перпендикулярной к плоскости α и к плоскости π₁.

Ход решения

1. Плоскость π₄ будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. При этом ось х₁₄ перпендикулярна к горизонтальной проекции h₁ горизонтали h плоскости α. Дополнительной ортогональной проекцией плоскости α на плоскость π₄ является прямая B₄C₄D₄ (рис.52 ).

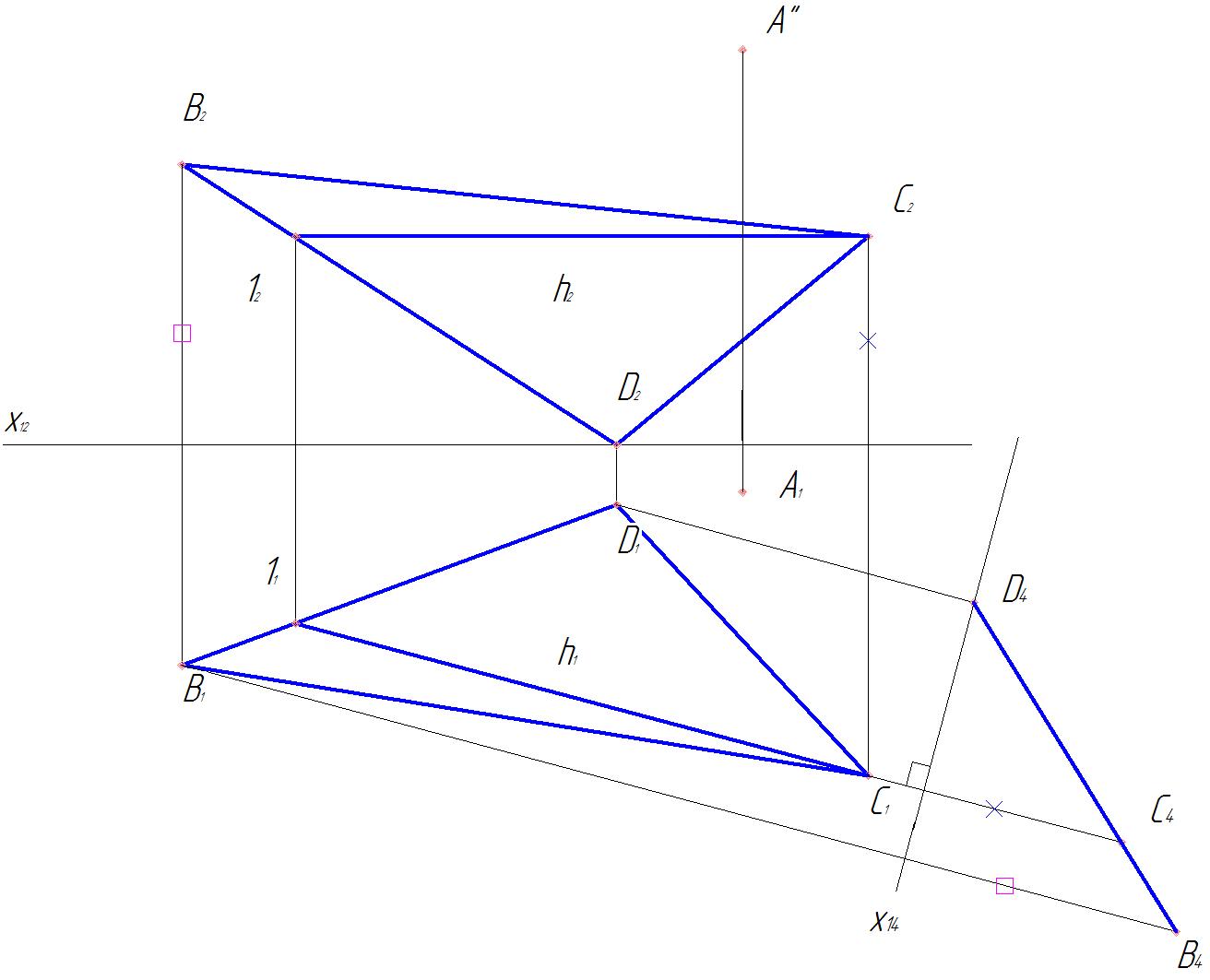
2. Из точки А₄ опускаем перпендикуляр А₄ K₄ на прямую B₄C₄D₄. Длина отрезка А₄K₄ равна расстоянию от точки А до плоскости α(ΔBCD) (рис.53 ).

Построим проекции отрезка АК. Горизонтальная проекция А₁К₁ параллельна оси х₁₄, так как отрезок АК параллелен плоскости π₄, и перпендикулярна к горизонтальной проекции h₁горизонтали h плоскости α. Фронтальную проекцию К₂ точки К строим по двум ее проекциям К₁ и K₄.

На основании решения рассмотренной задачи можно определить расстояние между параллельными прямой и плоскостью, между двумя параллельными плоскостями.

1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. – М.: Наука, 2000 – 272с.

2. Крылов Н.Н. Начертательная геометрия. – М.: Высшая школа, 2007 – 224с.

3. Локтев О.В. Краткий курс начертательной геометрии. – М.: Высшая школа, 2001 – 130с.

4. Фролов С.А. Начертательная геометрия. М.: Машиностроение, 1983 – 240с.

Источник