Как построить эпюр по координатам
Координатный способ построения эпюра точки
Модель положения точки в системе π1, π2, π3 (рис. 12) аналогична модели, которую можно построить, зная прямоугольные координаты этой точки, т.е. числа, выражающие ее расстояния от трех взаимно перпендикулярных плоскостей π1,π2,π3– плоскостей координат. Прямые (x, y, z), по которым пересекаются плоскости координат, называют осями координат. Точка пересечения осей
координат называется началом координат и обозначается цифрой О.
Оси координат называют: x – абсциссой, y – ординатой, z – аппликатой. Координаты точек записывают в определенной последовательности: сначала указывают значение координаты по оси x, затем по y, далее по z, например, если: Ах = 20; Ау = 15; Аz = 25, то координаты точки А следует записать:
Построенный на рисунке 12 параллепипед называют параллепипедом точки А. При построении параллепипедов координат нужно учесть, что проекции отрезков, откладываемых по оси y или параллельно ей сокращаются вдвое.
Плоскости координат в своем пересечении образуют восемь трехгранных углов, деля пространство на восемь частей – восемь октантов: I, II, III, IV, V, VI, VII, VIII (рис. 14).
Рис. 14
Плоская модель пространственного макета восьми октантов пространства показана на рисунке 15.
Рис. 15
Данная плоская модель пространственного макета несет такую же информацию, что и пространственный макет.
Данная координатная система является наиболее удобной для фиксирования положения геометрической фигуры в пространстве и выявления формы предмета по ортогональным (прямоугольным) проекциям.
Эта система называетсядекартова система координат, по имени французского математика и философа Декарта (1596 – 1650), предложившего эту систему.
Знаки координат в октантах
| Октант | Знаки координат | Октант | Знаки координат | ||||
| x | y | z | x | y | z | ||
| I | + | + | + | V | — | + | + |
| II | + | — | + | VI | — | — | + |
| III | + | — | — | VII | — | — | — |
| IV | + | + | — | VIII | — | + | — |
Эпюр данной точки А выполнен на рисунке 16.
Рис. 16
Конкурирующие точки
Точки, которые расположены на одном и том же проецирующем луче, т.е. одноименные проекции которых совпадают, называют конкурирующими.
Рассмотрим точки А и В, расположенные на одном проецирующем луче S1 (S1┴π1). Горизонтальные проекции этих точек совпадают (А’≡В’).
Рис. 17 Рис. 18
Точка А закрывает собой точку В при проецировании на плоскость проекций π1, поэтому ее горизонтальная проекция будет видима, а у точки В – невидима.
б)фронтально – конкурирующие точки (рис. 19, 20);
Рассмотрим точки С и D, расположенные на одном проецирующем луче S2 (S2┴π2). Фронтальные проекции этих точек совпадают (C»≡D»).
Рис. 19 Рис. 20
Точка D закрывает собой точку С по отношению к плоскости проекций π2,поэтому на фронтальной проекции точка С будет невидима, а точка D – видима.
в) профильно – конкурирующие точки (рис. 21,22);
Рассмотрим точки Е и F, расположенные на одном проецирующем луче S3(S3┴π3). Профильные проекции этих точек совпадают (E»’≡F»’).
Рис. 21 Рис. 22
Точка Е закрывает собой точку F по отношению к плоскости проекций π3, поэтому на профильной проекции точка Е будет видима, а точка F – невидима.
Контрольные вопросы
1.Значение начертательной геометрии в решении инженерно-технических задач.
2. Назовите виды проецирования.
3. В чем заключается способ образования эпюра Монжа?
4. Как образуется система трех плоскостей проекций?
5. В чем сущность координатного способа построения эпюра точки?
6. Что позволяют определять конкурирующие точки?
Рекомендуемая литература
1. Фролов, С.А. Начертательная геометрия: Учебник. 3-е изд., перераб. и доп. – М.: ИНФРА, 2010. – 285 с.
1. Чекмарев А.А. Начертательная геометрия и черчение: Учеб.для студ. высш. учеб. Заведений. – 2 – е изд., перераб. и доп. – М.: Гуманит. изд. центр ВЛАДОС, 2005. – 471 с.: ил.
3. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М.: Высш. шк., 2009. – 272 с.:ил.
4. Петлина Т.П. Начертательная геометрия. Ортогональные проекции и их преобразование: Учеб.пособие (с примерами практического использования в курсовом и дипломном проектировании). – Самара: СамВен, 2005. – 168 с.
Лекция №2
Прямая. Точка на прямой. Задание и изображение чертежа. Следы прямой. Положение прямой относительно плоскостей проекций. Взаимное расположение двух прямых. Безосный чертёж.
План лекции.
2. Положения прямой относительно плоскостей проекций.
4. Построениенатуральной величины отрезка прямой методом прямоугольного треугольника
5. Взаимное расположение прямых.
Проекции прямой
При ортогональном проецировании на плоскость прямая, не перпендикулярная плоскости проекций, проецируется в прямую. В противоположном случае она спроецируется на плоскость в точку.
Для определения проекций прямой достаточно знать проекции двух точек, принадлежащих этой прямой.
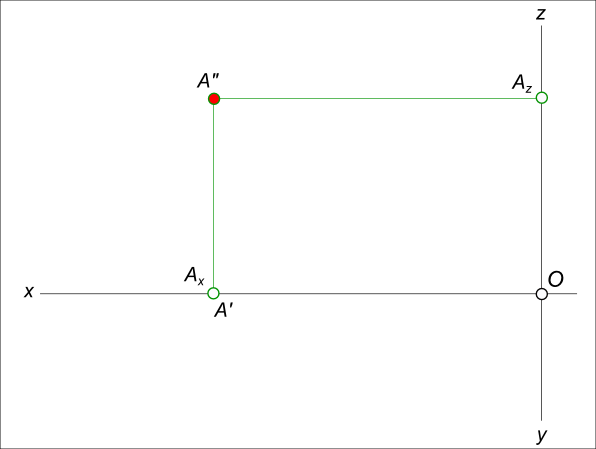
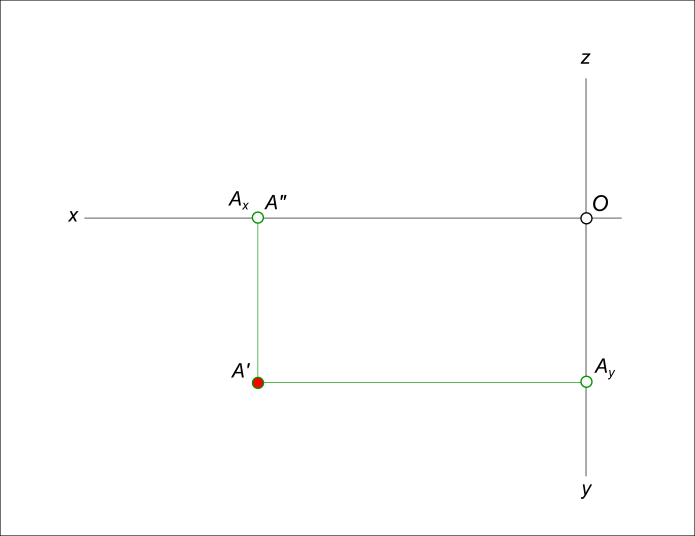
Допустим, что даны фронтальные и горизонтальные проекции точек А и В. Проведя через одноименные проекции этих точек прямые линии, получим проекции отрезка АВ в системе π1, π2 (рис. 1).
Рис. 1
Можно утверждать, что такой чертеж (рис. 1) выражает отрезок прямой линии АВ, т.к. если представить себе, что через А′ В′ и через А′′ В′′ проведены проецирующие плоскости (т.е. перпендикулярные соответственно к π1 и к π2), то в пересечении этих плоскостей получается прямая и ее отрезок АВ (рис.2).
Рис. 2
Проекции прямой могут быть заданы положением относительно осей проекций.
Проекции заданных таким образом прямых обозначаются малыми латинскими буквами (рис. 3 ).
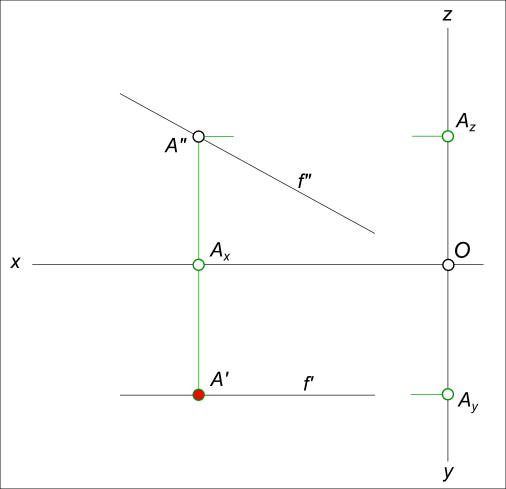
Эпюра точки
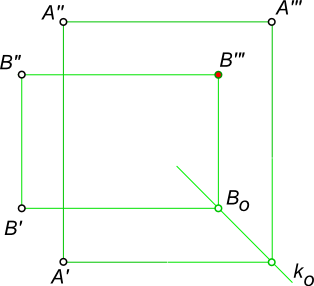
Задача № 1. Выполнить построение эпюра точки B(x, y, z), по двум известным проекциям точки построить третью.
| Выполняемое действие | Задаваемое положение | Достигнутая цель |
| строим A»`A0, A`A0 | A»`A0 ║ z, A`A0 ║ x | A»`A0 ∩ A`A0 = A0 ⇒ k0 |
| строим B`B0, B0B»` ∧ B»B»` | B`B0 ║ x, B0B»` ║ z, B»B»` ║ x | B0B»` ∩ B»B»` = B»` |
Задача №2. Выполнить построение эпюра точки A(x, y, z),принадлежащей только фронтальной плоскости проекций: y = 0.
Задача №3. Выполнить построение эпюра точки A(x, y, z),принадлежащей только горизонтальной плоскости проекций: z = 0.
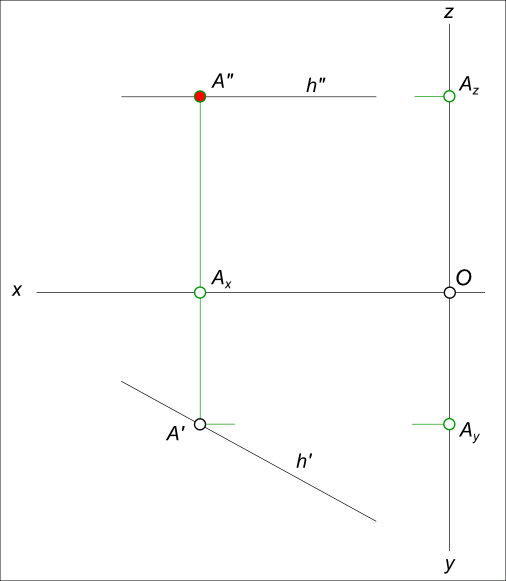
Задача №4. Дана горизонтальная прямая h. Выполнить построение эпюра точки A(A`, A»), принадлежащей прямой h.
| Выполняемое действие | Задаваемое положение | Достигнутая цель |
| откладываем x | Ax | |
| строим линию связи | ⊥ оси x | AxA» ∩ h» = A» |
| строим линию связи | ⊥ оси x | AxA` ∩ h` = A` |
Задача №5. Дана фронтальная прямая f. Выполнить построение эпюра точки точки A(A`, A»), принадлежащей фронтальной прямой f.
| Выполняемое действие | Задаваемое положение | Достигнутая цель |
| откладываем x | Ax | |
| строим линия связи | ⊥ оси x | AxA» ∩ f» = A» |
| строим линия связи | ⊥ оси x | AxA` ∩ f` = A` |
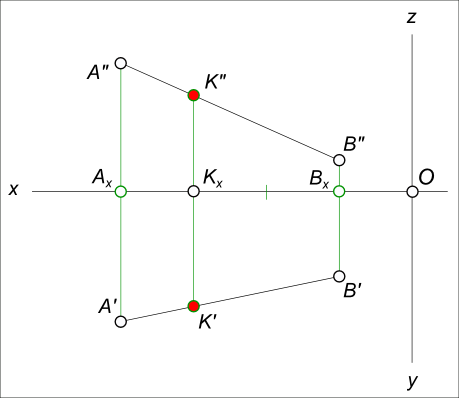
Задача №6. Дан отрезок прямой [AB]. Выполнить построение эпюра точки K(K`, K»), принадлежащей отрезку прямой [AB] и делящей его в отношении [AK]/[KB]=1/2.
| Выполняемое действие | Задаваемое положение | Достигнутая цель |
| делим [AxBx] на 3 равные части | Kx | |
| строим линию связи | ⊥ оси x | KxK» ∩ [A»B»] = K» |
| строим линию связи | ⊥ оси x | KxK` ∩ [A`B`] = K` |
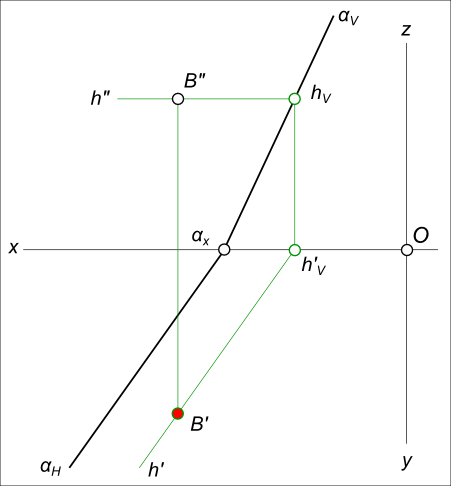
Задача №7. Дана фронтальная проекция точки B, принадлежащей плоскости α. Построить недостающую проекцию точки B.
Задача № 8. Дана горизонтальная проекция точки A, принадлежащей плоскости α(b ║ c). Построить недостающую проекцию точки A.
iSopromat.ru
Построение эпюр
Примеры решения задач на построение эпюр в сопротивлении материалов, строительной и технической механике со всеми расчетами, подробными пояснениями и видеоуроками.
Здесь рассмотрены примеры и порядок расчета значений внутренних силовых факторов, напряжений и перемещений и построения по ним эпюр для всех видов нагружения балок, стержней и валов.
Примеры построения эпюр
При растяжении-сжатии
Примеры построения эпюр внутренних продольных сил, нормальных напряжений и линейных перемещений для стержней при их растяжении и сжатии.
При кручении
Примеры построения эпюр внутренних крутящих моментов и угловых перемещений сечений вала при кручении.
Построение эпюр при изгибе
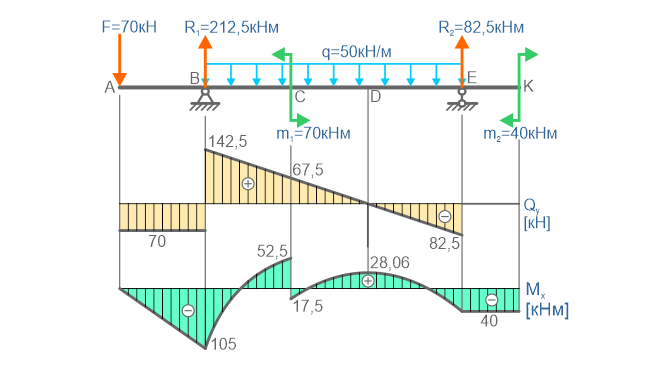
Примеры построения эпюр внутренних поперечных сил и изгибающих моментов, нормальных и касательных напряжений для балок и рам при изгибе.
Эпюры внутренних силовых факторов
Эпюры напряжений
Наш плейлист с видеоуроками построения эпюр внутренних силовых факторов, напряжений и перемещений для балки:
Порядок построения эпюр
В рассмотренных выше примерах для построения эпюр выполняется следующая последовательность действий:
После построения эпюр желательно выполнять их проверку.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Лекция 2. ТОЧКА НА ЭПЮРЕ МОНЖА
2.1. Аппарат полного проецирования.
2.3. Характеристика точек.
2.4. Контрольные вопросы.
Аппарат полного проецирования
Выше было указано, что бы обеспечить взаимно-однозначное соответствие между фигурами Ф пространства и их двумерными изображениями необходимо чтобы аппарат проецирования имел несколько плоскостей проецирования.
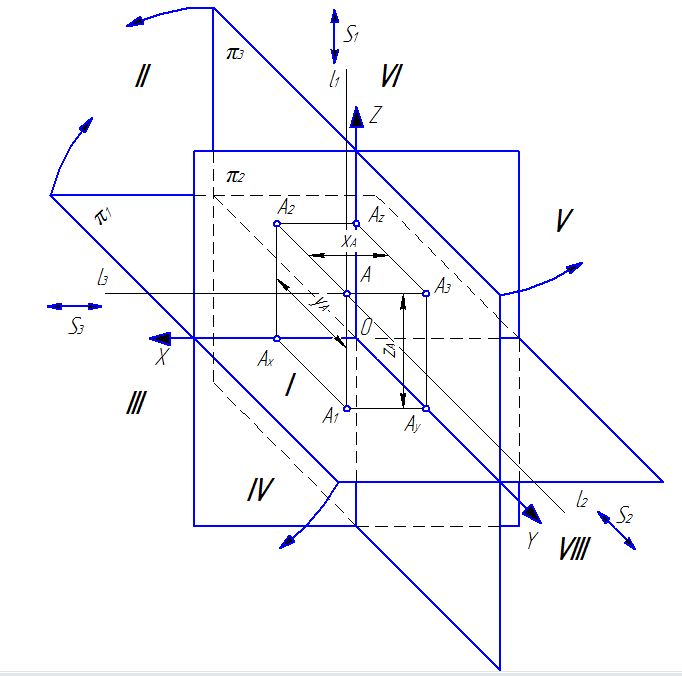
Рассмотрим аппарат полного проецирования (метод трех изображений). Для этого введём три плоскости проекций (рис. 14):
π1 – горизонтальная плоскость проекций;
π2 – фронтальная плоскость проекций;
π3 – профильная плоскость проекций.
Плоскости проекций располагаются взаимно перпендикулярно (π1^π2^ π3), а их линии пересечения образуют оси:
Точка пересечения осей считается точкой начала отсчета (точка 0).
Так как плоскости и оси взаимно перпендикулярны, то такой аппарат аналогичен декартовой системе координат.
Плоскости проекций все пространство делят на восемь октантов (на рис. 14 они обозначены римскими цифрами). Плоскости проекций считаются непрозрачными, а зритель всегда находится в I октанте.
Проецирование ортогональное с центрами проецирования S1, S2 и S3 соответственно для горизонтальной, фронтальной и профильной плоскостей проекций.
Рассмотрим работу аппарата на примере проецирования точки А.
Из центров проецирования S1, S2 и S3 выходят проецирующие лучи l1, l2 и l3. Эти лучи проходят через точку А и пересекаясь с плоскостями проекций образуют ее проекции:
– А1 – горизонтальная проекция точки А;
– А2 – фронтальная проекция точки А;
– А3 – профильная проекция точки А.
Точка в пространстве характеризуется своими координатами A(x,y,z). Точки Ax, Ay и Az соответственно на осях 0X, 0Y и 0Z показывают координаты x, y и z точки А. На рис. 14 даны все необходимые обозначения и показаны связи между точкой А пространства, её проекциями и координатами.
Эпюр точки
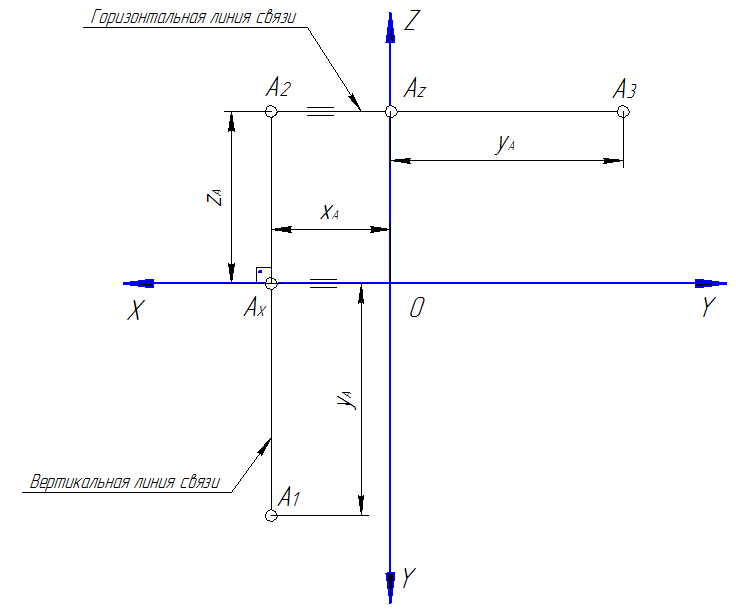
Чтобы получить чертёж точки А (рис. 15), в аппарате проецирования (рис. 14) плоскость π1 с полученной проекцией точки А1 вращают по часовой стрелке вокруг оси 0Х, до совмещения её с плоскостью π2. Затем плоскость π3 с проекцией точки А3, вращают против часовой стрелки вокруг оси 0Z, до совмещения её с плоскостью π2. Направление поворотов плоскостей π2 и π3 показано на рис. 13 стрелками. Полученный таким образом чертёж называется эпюром. При этом прямые А1Ах и А2Ах станут располагаться на общем к оси 0Х перпендикуляре А1А2, а прямые А2Ах и А3Ах станут располагаться на общем к оси 0Z перпендикуляре А2А3. Эти прямые в дальнейшем будем называть соответственно вертикальной и горизонтальной линиями связей.
Следует отметить, что при переходе от аппарата проецирования к эпюру проектируемый объект исчезает, но вся информация о его форме, геометрических размерах и месте его положения в пространстве сохраняются.
На практике построение эпюра точки А(xA, yA, zA) осуществляется по численным значениям ее координат xA, yA и zA в следующей последовательности (рис. 15). Эта последовательность называется методикой построения эпюра точки.
1. Ортогонально вычерчиваются оси OX, OY и OZ.
2. На оси OX откладывается численное значение координаты xA точки А и получают положение точки Ах.
3. Через точку Ах перпендикулярно оси OX проводится вертикальная линия связи.
4. На вертикальной линии связи от точки Ах по направлению оси OY откладывается численное значение координаты yA точки А и определяется положение горизонтальной проекции точки А1 на эпюре.
5. На вертикальной линии связи от точки Ах по направлению оси OZ откладывается численное значение координаты zA точки А и определяется положение фронтальной проекции точки А2 на эпюре.
6. Через точку А2 параллельно оси OX проводится горизонтальная линия связи. Пересечение этой линии и оси OZ даст положение точки Аz.
7. На горизонтальной линии связи от точки Аz по направлению оси OY откладывается численное значение координаты yA точки А и определяется положение профильной проекции точки А3 на эпюре.
Характеристика точек
Все точки пространства подразделяются на точки частного и общего положений.
Точки частного положения. Точки, принадлежащие аппарату проецирования, называются точками частного положения. К ним относятся точки, принадлежащие плоскостям проекций, осям, началу координат и центрам проецирования. Характерные признаки точек частного положения приведены в табл. 1 и на рис. 16–19.
Математические признаки точек частного положения
| Точка принадлежит | Численные значения координат точки | ||
| x | y | z | |
| плоскости π1 | ≠0 | ≠0 | =0 |
| плоскости π2 | ≠0 | =0 | ≠0 |
| плоскости π3 | =0 | ≠0 | ≠0 |
| оси 0X | ≠0 | =0 | =0 |
| оси 0Y | =0 | ≠0 | =0 |
| оси 0Z | =0 | =0 | ≠0 |
| точки 0 | =0 | =0 | =0 |
| центру S1 | ≠0 | ≠0 | ∞ |
| центру S2 | ≠0 | ∞ | ≠0 |
| центру S3 | ∞ | ≠0 | ≠0 |
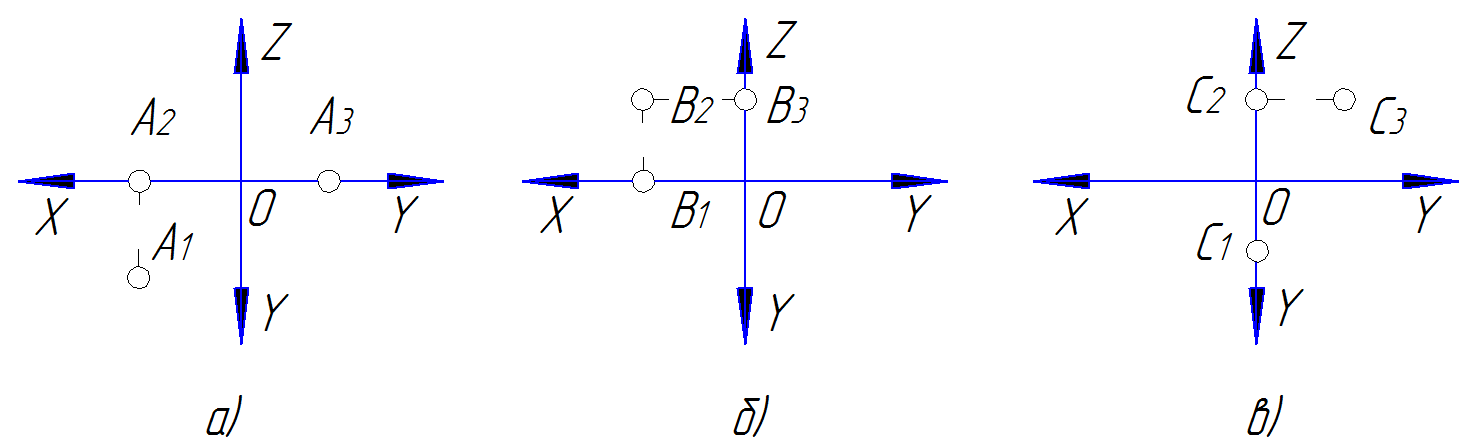
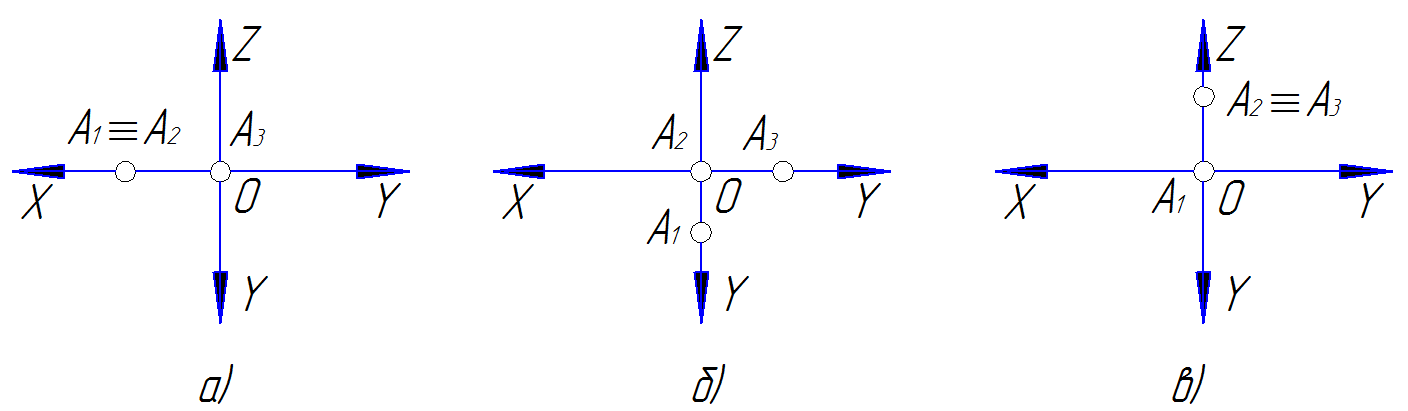
На рис. 16 приведены характерные признаки принадлежности точек плоскостям проекций на эпюре Монжа: точка А Ì π1 (рис 16а); точка В Ì π2(рис 16б); точка С Ìπ3 (рис 16в). Такими признаками являются принадлежность двух проекций точки осям.
На рис. 17 приведены характерные признаки принадлежности точек осям на эпюре Монжа: точка А Ì0X (рис 17а); точка В Ì 0Y (рис 17б); точка С Ì0Z (рис 17в). Такими признаками являются принадлежность двух тождественно совпадающих проекций точки осям эпюра.
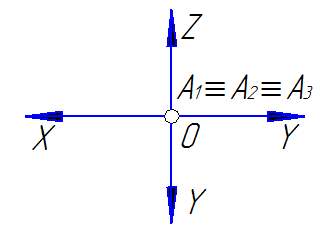
На рис 18 на эпюре Монжа показан характерный признак точки А принадлежащей началу координат, т.е. все три проекции точки тождественно совпадают и принадлежат началу координат.
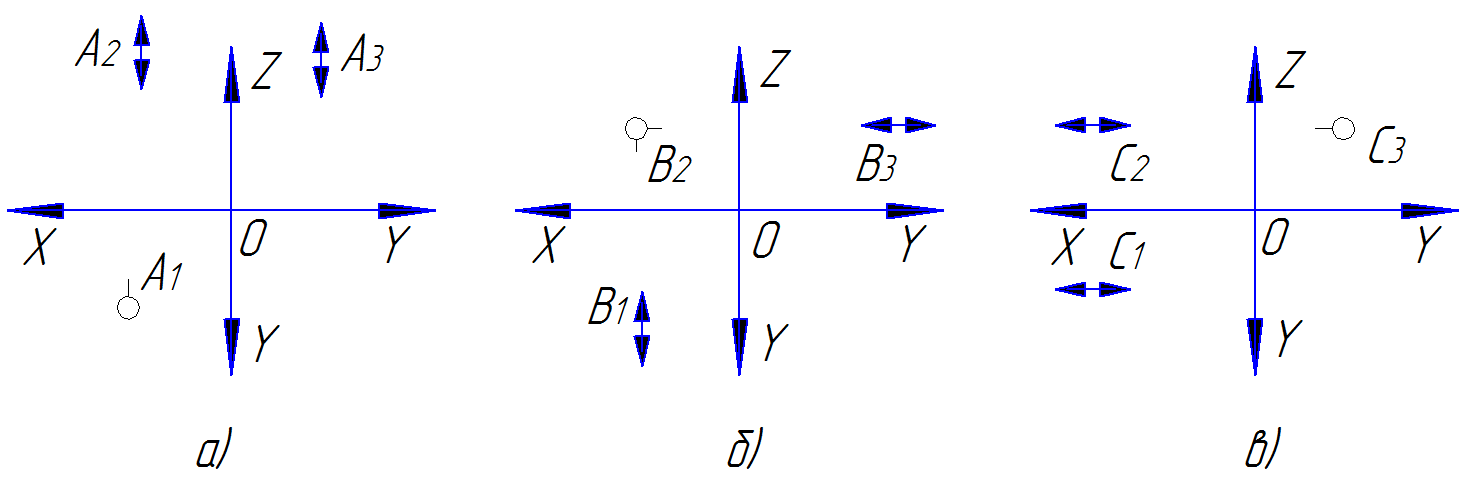
На рис. 19 приведены характерные признаки принадлежности точек центрам проецирования на эпюре Монжа: точка А Ì S1 (рис 19а); точка
В Ì S2(рис 19б); точка С Ì S3 (рис 19в). Такими признаками являются принадлежность двух проекций точки проекциям центров проецирования.
Точки общего положения. К точкам общего положения относятся точки, не принадлежащие аппарату проецирования. Например, точка на рис. 13.
В общем случае численные значения координат точки характеризует ее удаление от плоскости проекций: координата х от плоскостиπ3; координата y от плоскости π2; координата z от плоскости π1. Следует отметить, что знаки при численных значениях указывают на направление удаления точки от плоскостей проекций. В зависимости от сочетания знаков при численных значениях координат точки зависит в каком из октанов она находится (табл. 2).
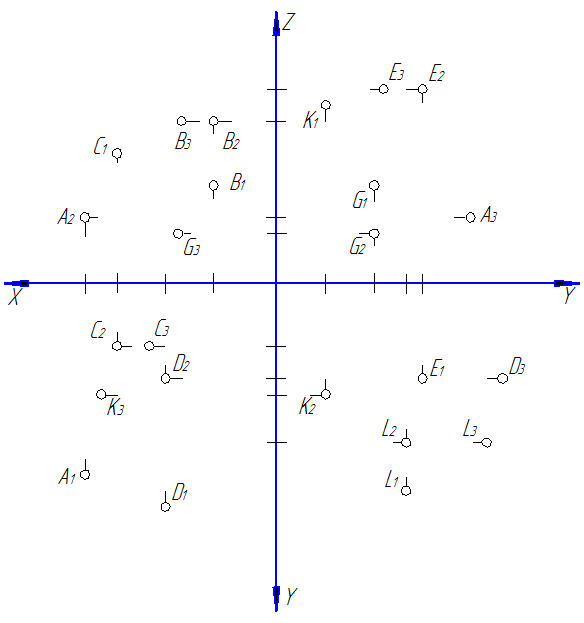
Расположение проекций точки, относительно осей, на эпюре зависит от того в каком октане она находится (рис. 20).
На рис. 20 показано расположение проекций относительно осей для точки: А находящейся в I октане; В находящейся во II октане; C находящейся в III октане; D находящейся в IV октане; E находящейся в V октане; G находящейся в VI октане; K находящейся в VII октане; L находящейся в VIII октане.
Определение номера октана от знаков координат
| Номер октана | Знак при координате | ||
| x | y | z | |
| I | + | + | + |
| II | + | — | + |
| III | + | — | — |
| IV | + | + | — |
| V | — | + | + |
| VI | — | — | + |
| VII | — | — | — |
| VIII | — | + | — |
2.4. Контрольные вопросы
1. Как называются плоскости проекций π1,π2и π3?
2. Как образуются оси 0Х, 0Y и 0Z?
3. Как получается проекции точи в аппарате проецирования?
4. Зачем нужны центры проецирования S1, S2 и S3?
5. Как осуществляется переход от аппарата проецирования к плоскому чертежу?
6. Чем отличается эпюр от аппарата проецирования?
7. Алгоритм построения точки на эпюре Монжа.
8. Какие точки относятся к точкам общего положения?
9. Какие точки относятся к точкам частного положения?
10. Характерные признаки точек частного положения на эпюре Монжа.
11. Что характеризуют численные значения координат х, y и z точки?
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.