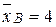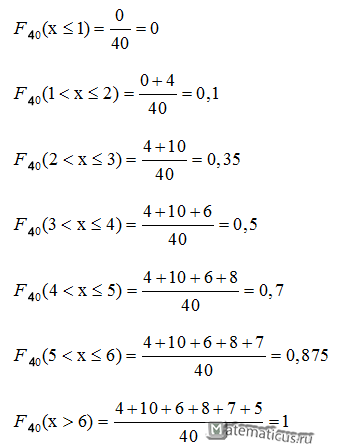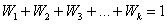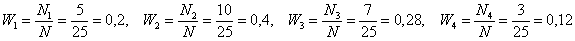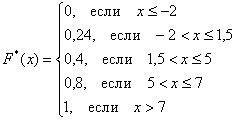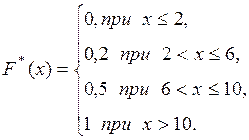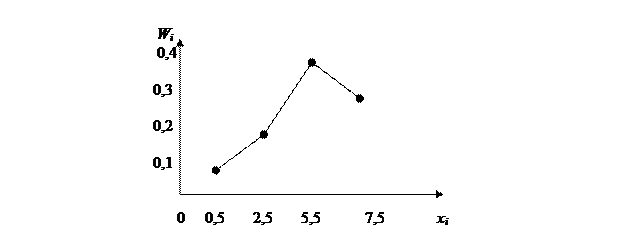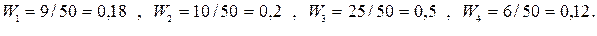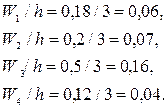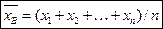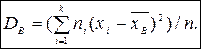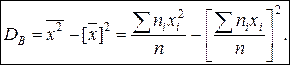Как построить эмпирическую функцию распределения
Эмпирическая функция распределения
Эмпирической (опытной) функцией распределения или функцией распределения выборки называют такую функцию, которая определяет для каждого значения x частоту событий X
Дана таблица функции распределения выборки. Требуется построить эмпирическую функцию распределения
| xi | 1 | 2 | 3 | 4 | 5 | 6 |
| ni | 4 | 10 | 6 | 8 | 7 | 5 |
Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки
Эмпирическая функция распределения имеет вид
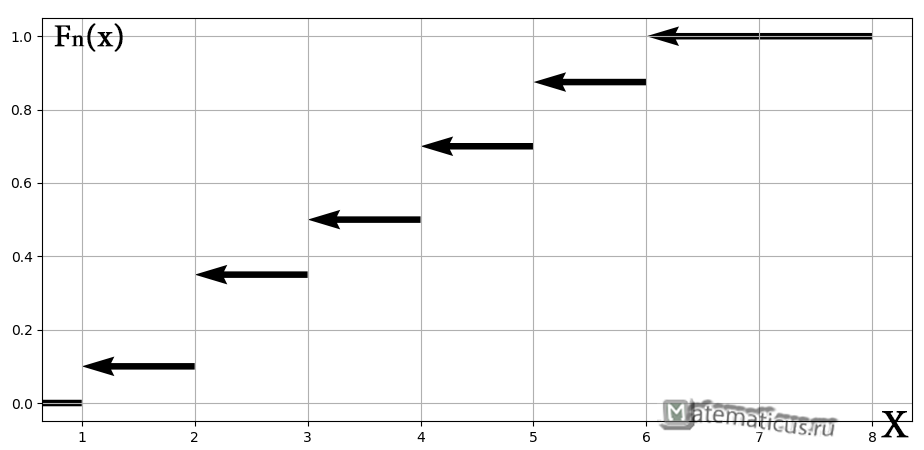
Построим график кусочно-постоянной эмпирической функции распределения
таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.7 / 5. Количество оценок: 38
Оценок пока нет. Поставьте оценку первым.
3 комментария
У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.
Исправили. Спасибо Вам большое за внимательность)
Не понял физического смысла эмпирического распределения — что она нам дает?
2. Дискретный вариационный ряд.
Полигон частот и эмпирическая функция распределения
На вводном уроке по математической статистике мы узнали, что такое математическая статистика, и теперь обо всём подробнее. Далее для удобства я буду нумеровать статьи и постараюсь делать их не слишком длинными. Потому что всё действительно просто, и главное, здесь научиться рациональной технике вычислений, на которую и будет сделан особый упор.
Интервальные и дискретные вариационные ряды почти сразу же встретились в предыдущей статье, и мы начинаем с дискретного случая, когда количественная эмпирическая величина 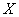
…что-то не понятно по терминам? Срочно изучать первый урок! (ссылка выше)
Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант 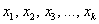
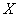
Частоты выборочной совокупности обозначают через 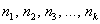
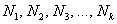
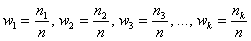
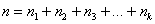
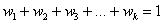
Аналогично для совокупности генеральной: 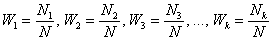
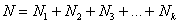
И тут вспоминается Пример 2 об оценках по матанализу в группе из 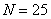
– пожалуйста, пример дискретного вариационного ряда, где варианты 
Для разминки найдём относительные частоты:
и непременно проконтролируем, что: 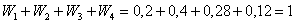
Все вычисления обычно проводят на калькуляторе либо в Экселе, а результаты заносят в таблицу, при этом, в статистике данные чаще располагают не в строках, а в столбцах: 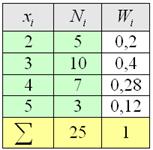
Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в строчку. Не редкость, когда их 10-20, а бывает, и 100-200, что тоже и неоднократно встречалось в моей практике. И это не какие-то супер-пупер расчёты, а учебные задачи!
После сей позитивной новости продолжаем 🙂
Откуда берутся дискретные вариационные ряды? Такие ряды появляются в результате учёта дискретной характеристики статистической совокупности, причём, варианты ряда не отличаются большим разнообразием. Например, оценки (коих не так много) в примере выше.
И сейчас мы примем непосредственное участие в этом процессе:
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3. Требуется:
– составить вариационный ряд и построить полигон частот;
– найти относительные частоты и построить эмпирическую функцию распределения.
Чего томиться? – вся тема урока в одной задаче!
Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. В данном случае это легко сделать устно: 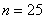
Квалификационные разряды – есть величина дискретная, и поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).
Если у вас под рукой нет вычислительных программ, то вручную (Эксель разберём ниже). При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка: 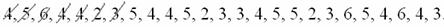
и делать около соответствующих кружков засечки:
После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке: 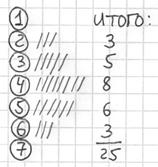
И обязательно проверяем, получается ли у нас в сумме объём выборки 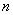

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяют достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)
Построенный вариационный ряд также называют статистическим распределением выборки, причём, этот термин применИм не только для дискретного, но и для интервального ряда, который мы рассмотрим на следующем уроке.
Построим полигон частот. Это статистический аналог многоугольника распределения дискретной случайной величины (кто изучал). Полигон частот – это ломаная, соединяющая соседние точки 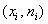
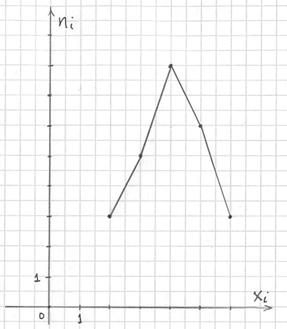
…эх, ностальгия. Но, пятилетку-другую, думается, так решать ещё будут.
Теперь современный способ:
Решаем! – исходные данные с пошаговой инструкцией прилагаются.
Вторая часть задачи. Найдём относительные частоты 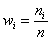

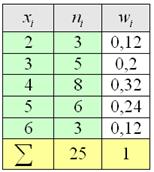
– обязательно проверяем, что сумма относительных частот равна единице!
Иногда требуется построить полигон относительных частот. Как вы правильно догадываетесь – это ломаная, соединяющая соседние точки 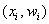
А теперь посмотрим на относительные частоты и задумаемся, на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что 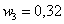
А вот если учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты 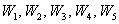
Построим эмпирическую функцию распределения 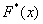
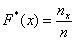
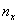
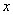
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Очевидно, что на интервале 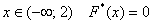
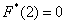
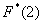
На промежутке 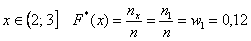
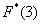
На промежутке 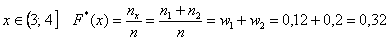
– если 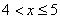

– если 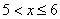
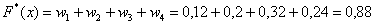
– и, наконец, если 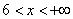
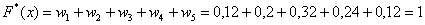
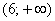
Накопленные относительные частоты удобно записывать в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева 1-е значение (красная стрелка), а каждое следующее получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения): 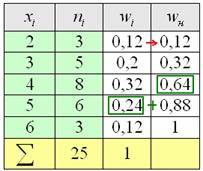
Вот, кстати, ещё один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
Саму функцию принято записывать в кусочном виде:
а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения из промежутка 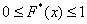
И сейчас мы автоматизируем процесс; видео, к сожалению, не вписалось по ширине, посему смотрим его на Ютубе:

Эмпирическая функция распределения 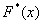
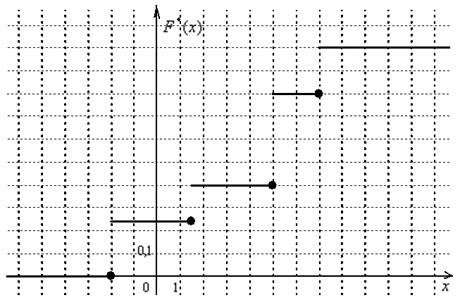
Миниатюрная задача для закрепления материала:
Дано статистическое распределение выборки
Составить эмпирическую функцию распределения, выполнить чертёж
Самостоятельно решить Пример 5 в Экселе, все числа и обозначения уже там.
Свериться с образцом можно ниже. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
И я жду вас на третьем уроке, где речь пойдёт об интервальном вариационном ряде.
Пример 5. Решение: заполним расчётную таблицу:
Составим эмпирическую функцию распределения:
Выполним чертёж:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Эмпирическая функция распределения
Пусть известно статистическое распределение частот количественного признака Х. Введем обозначения: 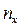
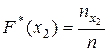
В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события X * (x) определяет относительную частоту этого же события.
Из теоремы Бернулли следует, что относительная частота события X * (x), стремится по вероятности к вероятности этого события, то есть к значению F(x). Другими словами, при больших значениях n числа F * (x) и F(x) мало отличаются одно от другого в том смысле, что 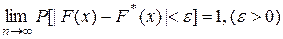
Из определения функции F * (x) вытекают следующие ее свойства:
1) Значения эмпирической функции принадлежит отрезку [0; 1];
2) F * (x) – неубывающая функция;
3) Если x1 ─ наименьшая варианта, то F * (x) = 0 при х * (x) = 1 при х > xk.
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
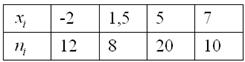
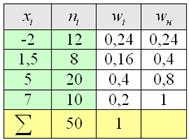
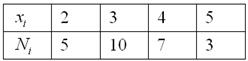
Пример. Построить эмпирическую функцию по данному распределению выборки:
Варианты  |
Частоты  |
Решение. Найдем объем выборки (сумма всех частот ni):
Наименьшая варианта равна 2 (x1 = 2), следовательно, F * (x) = 0 при х ≤ 2 (по свойству 3 функции F * (x));
значения, меньшие 6 (х * (x) = 1 при х>10 (по свойству 4 функции F * (x)).
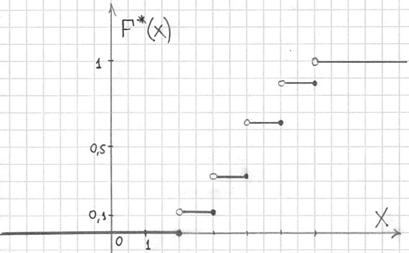
Искомая эмпирическая функция имеет вид:
Ниже приведен график полученной эмпирической функции.
На графике на соответствующих осях откладывают значения функции F * (x) и интервалы вариант
Рис. 5. График эмпирической функции.
Полигон и гистограмма
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Определение. Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, n1), (x2, n2), …, (xk, nk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.
Определение. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1, w1), (x2, w2), …, (xk, wk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат wi. Точки (xi, wi) соединяют отрезками прямых и получают полигон относительных частот.
На рисунке изображен полигон относительных частот следующего распределения:
| x | 1,5 | 3,5 | 5,5 | 7,5 |
| w | 0,1 | 0,2 | 0,4 | 0,3 |
Рис. 6. Полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-ый интервал.
Определение. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 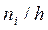
Рис. 7. Гистограмма частот.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии 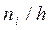
Площадь i-го частичного прямоугольника равна 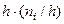

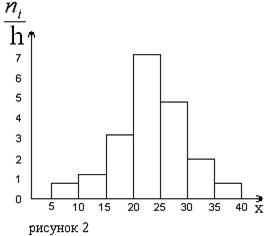
На рисунке 2 изображена гистограмма частот распределения объема n=100, приведенного в таблице 1.
| Частичный интервал, длиною h=5 | Сумма частот вариант частичного интервала  | Плотность частоты 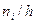 |
| 5 – 10 | 0,8 | |
| 10 – 15 | 1,2 | |
| 15 – 20 | 3,2 | |
| 20 – 25 | 7,2 | |
| 25 – 30 | 4,8 | |
| 30 – 35 | 2,0 | |
| 34 – 40 | 0,8 |
Определение. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длинною h, а высоты равны отношению 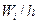
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии 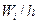
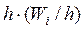
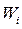
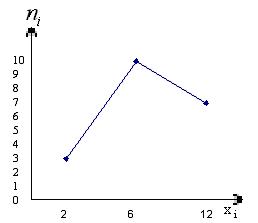
1. В результате выборки получена следующая таблица распределения частот.
 |
 |
Построить полигоны частот и относительных частот распределения.
Для начала построим полигон частот.
Рис. 8. Полигон частот.
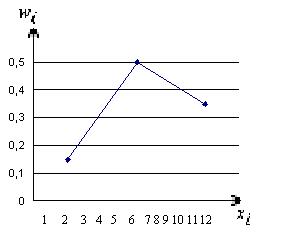
Чтобы построить полигон относительных частот найдем относительные частоты, для чего разделим частоты на объем выборки n.
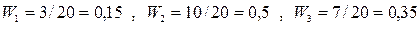
 | |||
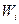 | 0,15 | 0,50 | 0,35 |
Построим полигон относительных частот.
Рис. 9. Полигон относительных частот.
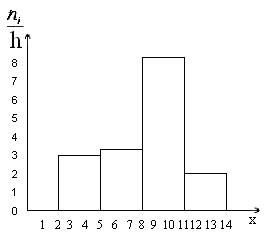
2. Построить гистограммы частот и относительных частот распределения.
Найдем плотность частоты 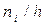
| Частичный интервал, длиною h = 3 | Сумма частот вариант частичного интервала  | Плотность частоты 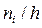 |
| 2 – 5 | ||
| 5 – 8 | 3,3 | |
| 8 – 11 | 8,3 | |
| 11 – 14 |
Построим гистограмму частот.
Рис. 10. Гистограмма частот.
Чтобы построить гистограмму относительных частот, нужно найти относительные частоты. Для этого найдем объем выборки n.
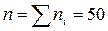
Теперь найдем относительные частоты 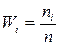
| Частичный интервал | Сумма относительных частот 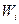 | Плотность частоты 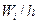 |
| 2 – 5 | 0,18 | 0,06 |
| 5 – 8 | 0,2 | 0,07 |
| 8 – 11 | 0,5 | 0,16 |
| 11 – 14 | 0,12 | 0,04 |
Плотности частот 
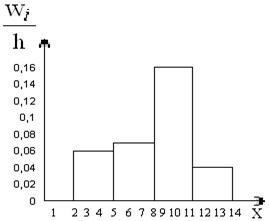
Построим гистограмму относительных частот.
Рис.11. Гистограмма относительных частот.
Точечные оценки
Определение. Статистической оценкой Q * неизвестного параметра Q теоретического распределения называют функцию f(x1, x2, …, xn) от наблюдаемых случайных значений x1, x2, …, xn.
Определение. Точечной оценкой называют статистическую оценку, которая определяется одним числом Q * = f(x1, x2, …, xn), где x1, x2, …, xn ─ результаты n наблюдений над количественным признаком Х (выборка).
Выборочная средняя.
Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.
Определение. Выборочной средней 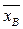
Если все значения x1, x2, …, xn признака выборки объема n различны, то
Если же все значения признака x1, x2, …, xk имеют соответственно частоты n1, n2, …, nk, причем n1 + n2 + … + nk = n, то
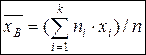
где 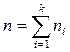
Выборочная средняя является несмещенной оценкой генеральной средней (неизвестного математического ожидания).
Замечание. Если первоначальные варианты 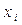
число С, то есть перейти к условным вариантам ui = xi – c. Тогда
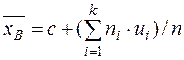
Выборочная дисперсия.
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия. Эту величину вводят для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг среднего значения 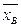
Определение. Выборочной дисперсией 
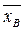
Эта оценка является смещенной, так как 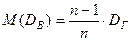
где DГ – генеральная дисперсия – среднее арифметическое квадратов отклонения значения признака генеральной совокупности от их среднего значения 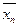
Теорема.Выборочная дисперсия равна среднему квадратов значений признака минус квадрат выборочной средней.
Для вычисления выборочной дисперсии эта формула наиболее удобна.
Оценка генеральной дисперсии по исправленной выборочной.
Пусть из генеральной совокупности в результате n независимых наблюдений
над количественным признаком Х извлечена повторная выборка объема n:
| Значения признака | xi | x1 | x2 | … | xk |
| Частоты | ni | n1 | n2 | … | nk |
При этом n1 + n2 + … + nk = n. Требуется по данным выборки найти неизвестную генеральную дисперсию DГ. Если в качестве оценки DГ принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение DГ. Объясняется это тем, что математическое ожидание выборочной дисперсии не равно оцениваемой DГ, а равно 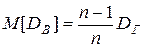
Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить 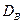
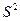
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:
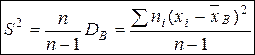
Более удобна форма:

В условных вариантах она имеет вид:
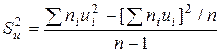
причем если ui = xi – c, то 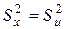
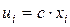
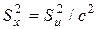
Из генеральной совокупности извлечена выборка объемом n = 60
 |
 |
Найти несмещенную оценку генеральной средней.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя: 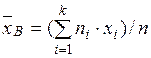
где 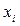
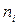

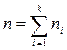
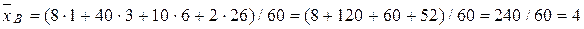
Ответ: