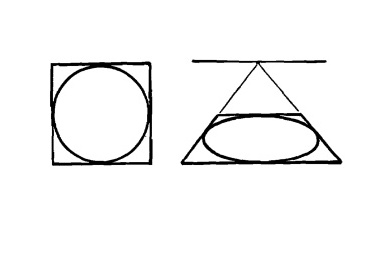Как построить эллипс в перспективе
Урок 3. Окружность в перспективе. Как нарисовать кружку и вазу
В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк. Сложность их изображения в пространстве заключается в том, что принцип равноудаленности точек окружности от центра срабатывает, только когда мы смотрим на плоскость прямо (то есть направление взгляда перпендикулярно ей). Например, мы видим круглый циферблат часов перед собой или чашку и блюдце, когда наклонились над ними. В других случаях (взгляд падает на плоскость под углом) мы видим искажение формы окружности, ее превращение в овал (эллипс).
Содержание:
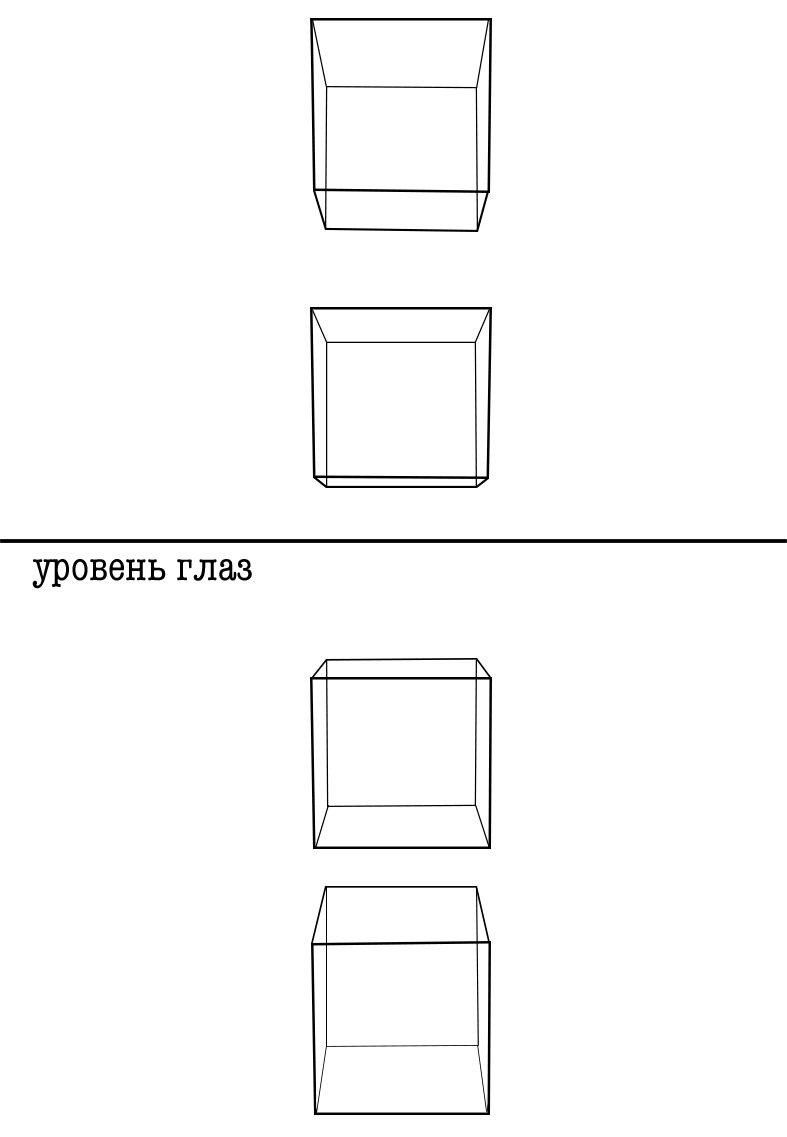
Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).
То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.
Принципы рисования эллипсов:
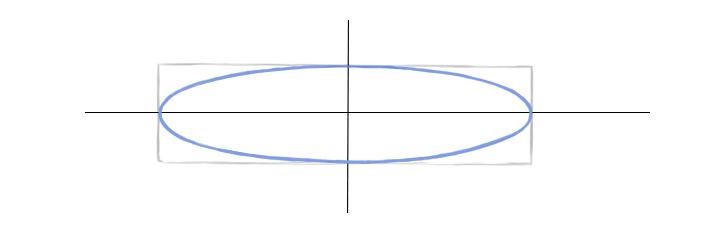
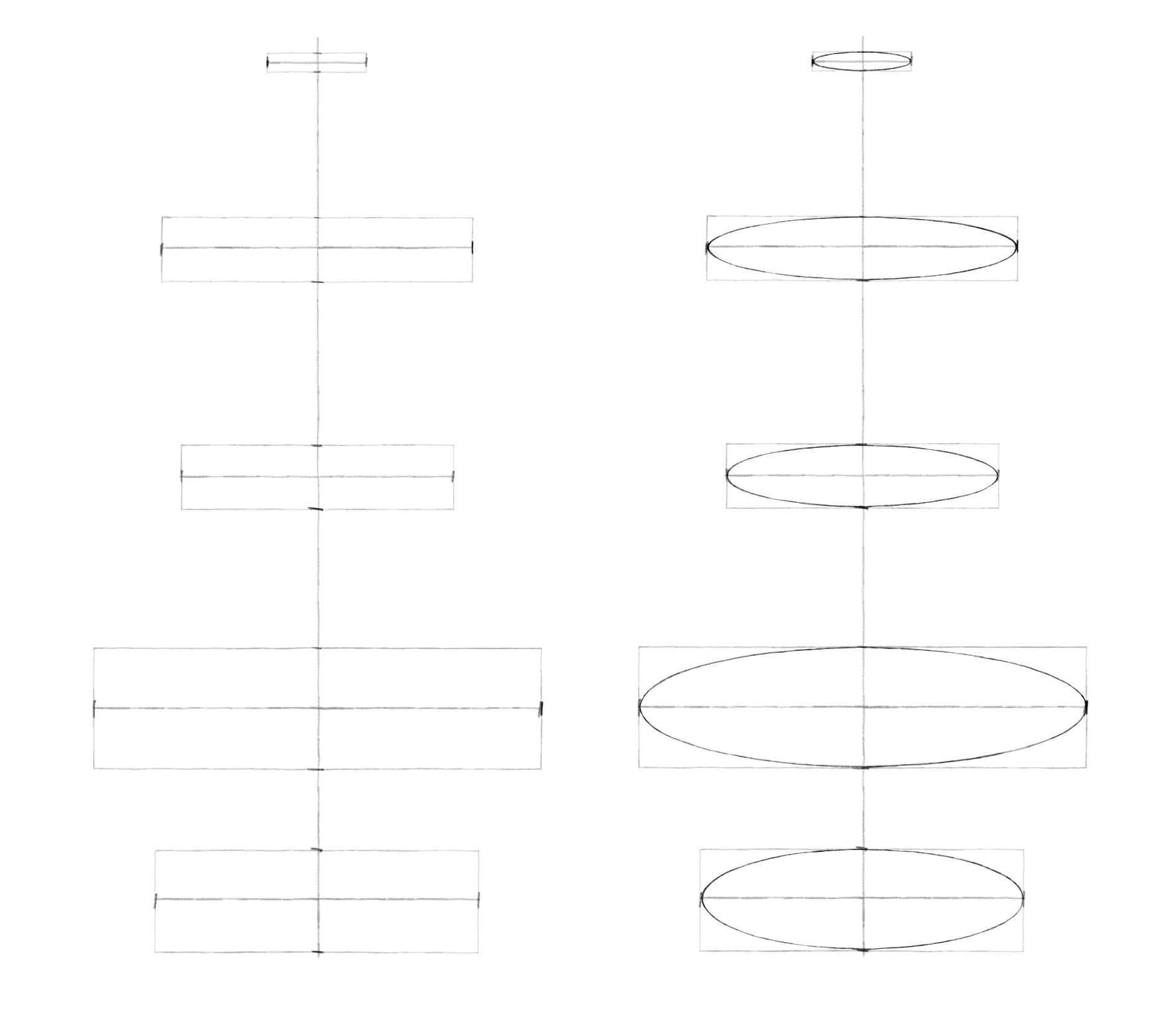
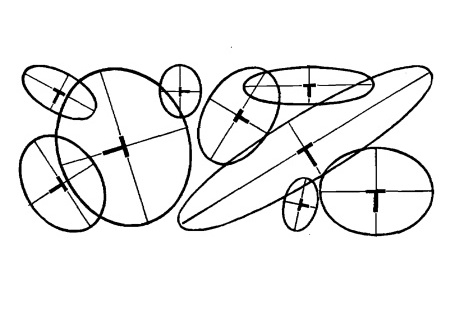
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.
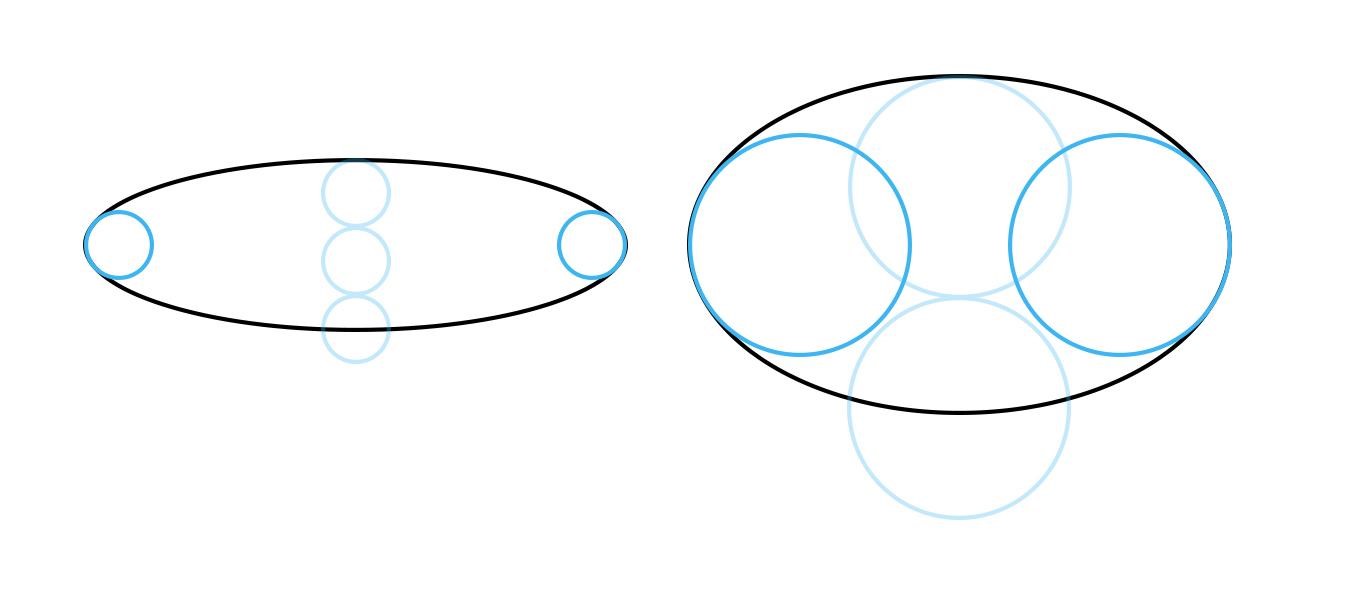
Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).
Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).
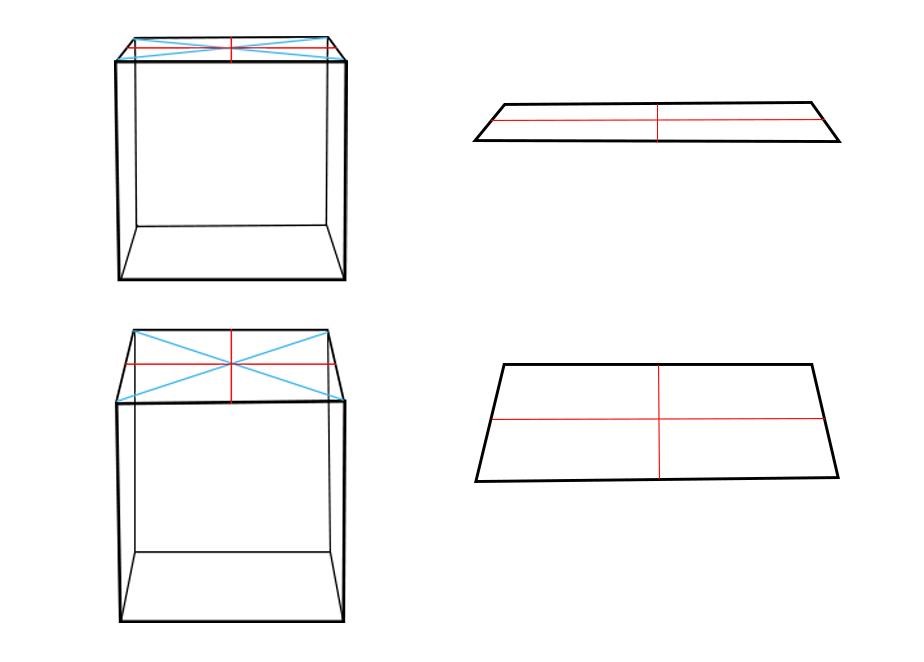
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.
Рисуем эллипсы
Шаг 1. Для начала проведем две перпендикулярных оси.
Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.
Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.
Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.
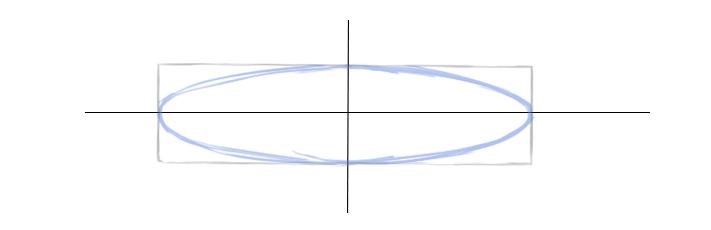
Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.
Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.
Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.
Рисуем кружку
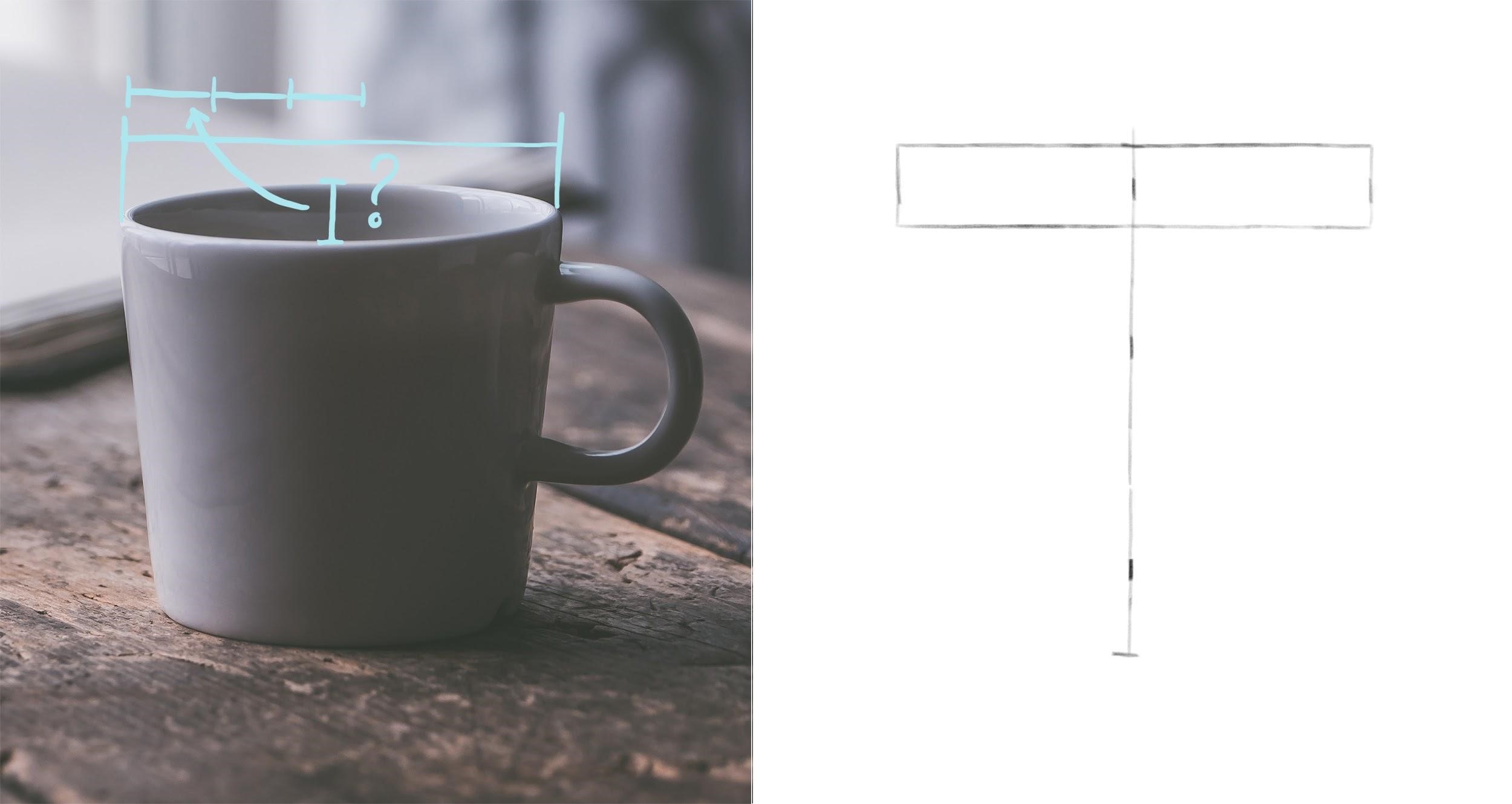
Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.
Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.
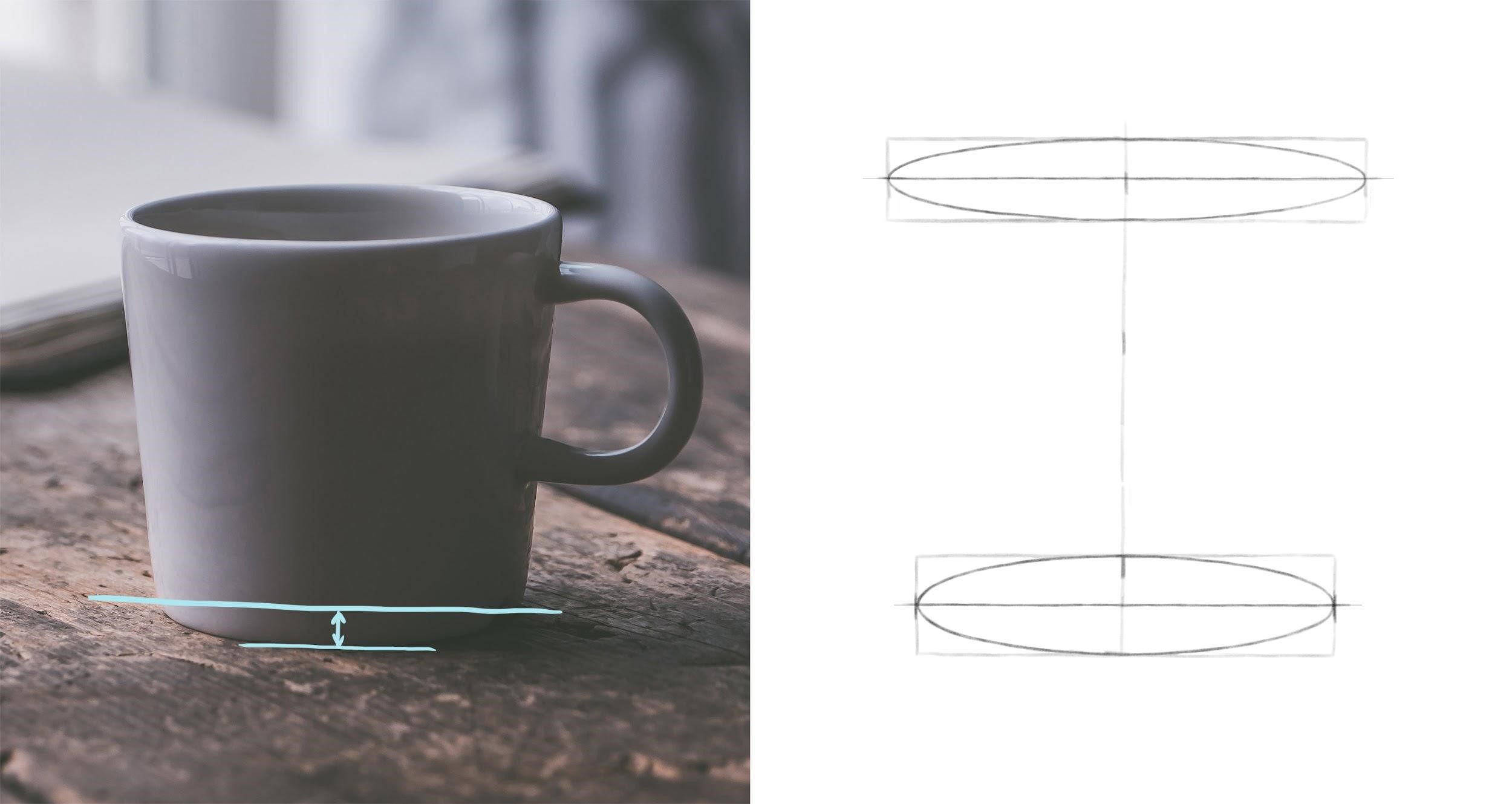
Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.
Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.
Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!
Рисуем вазу
В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.
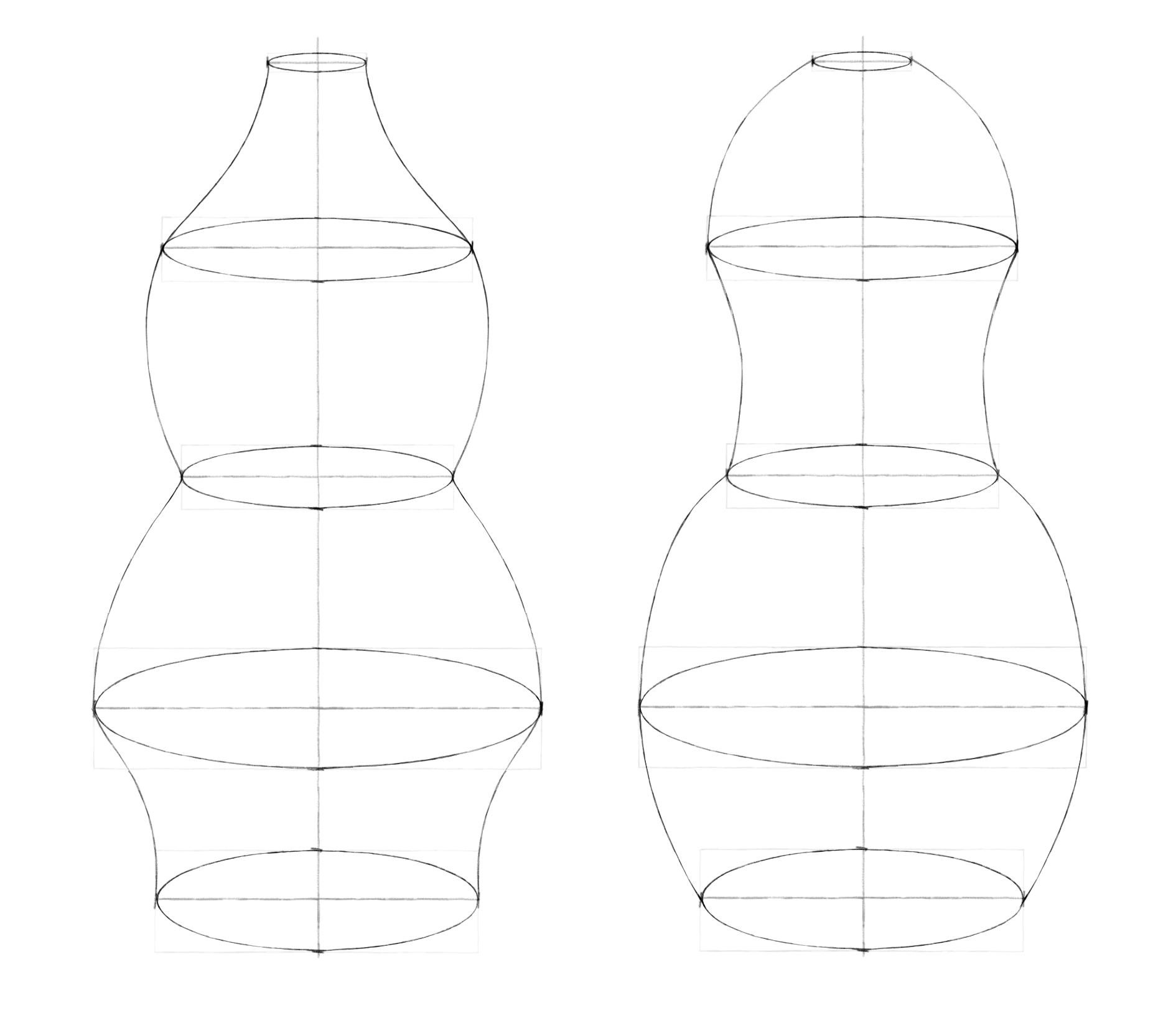
В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).
Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.
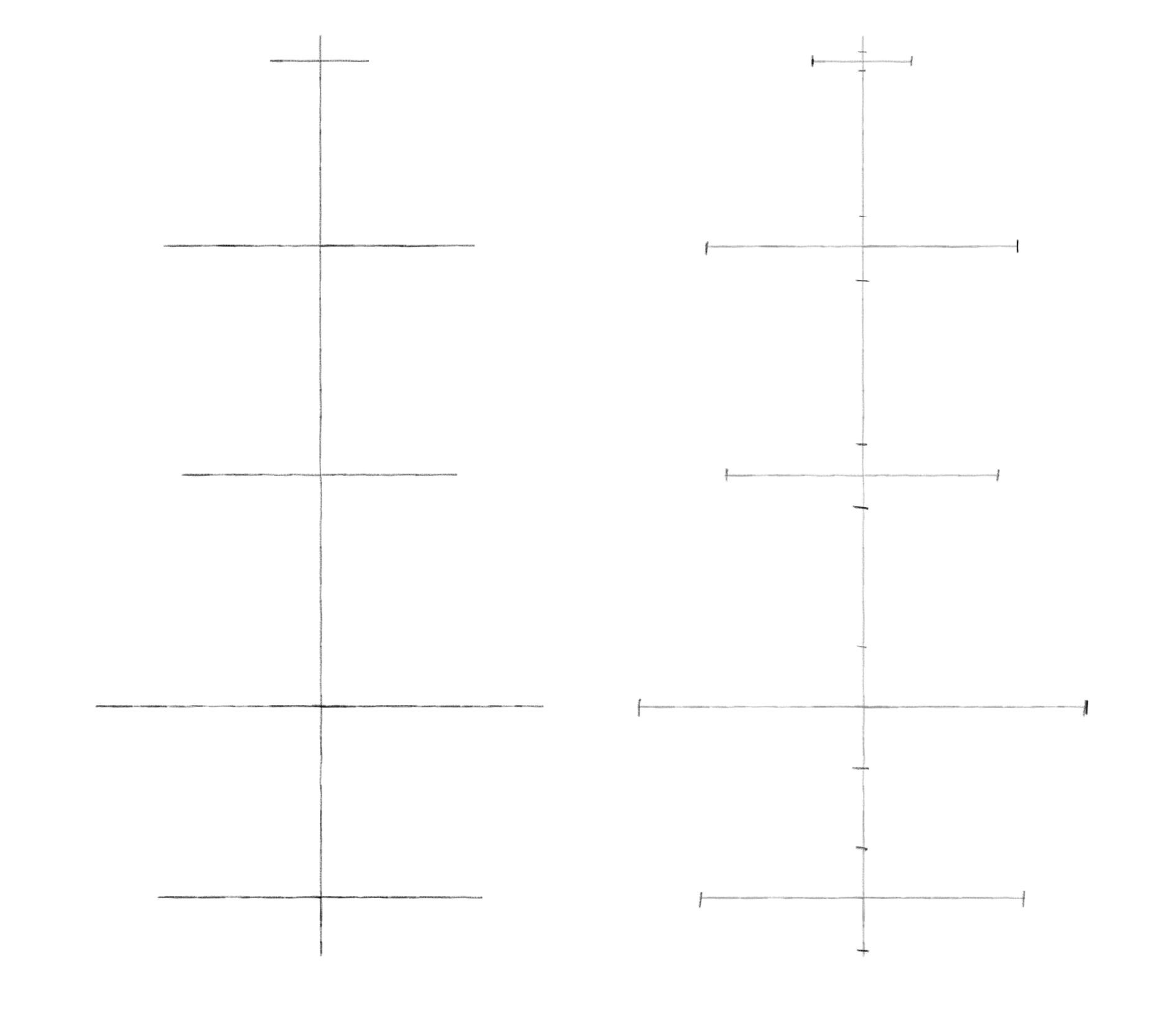
Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.
Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).
Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.
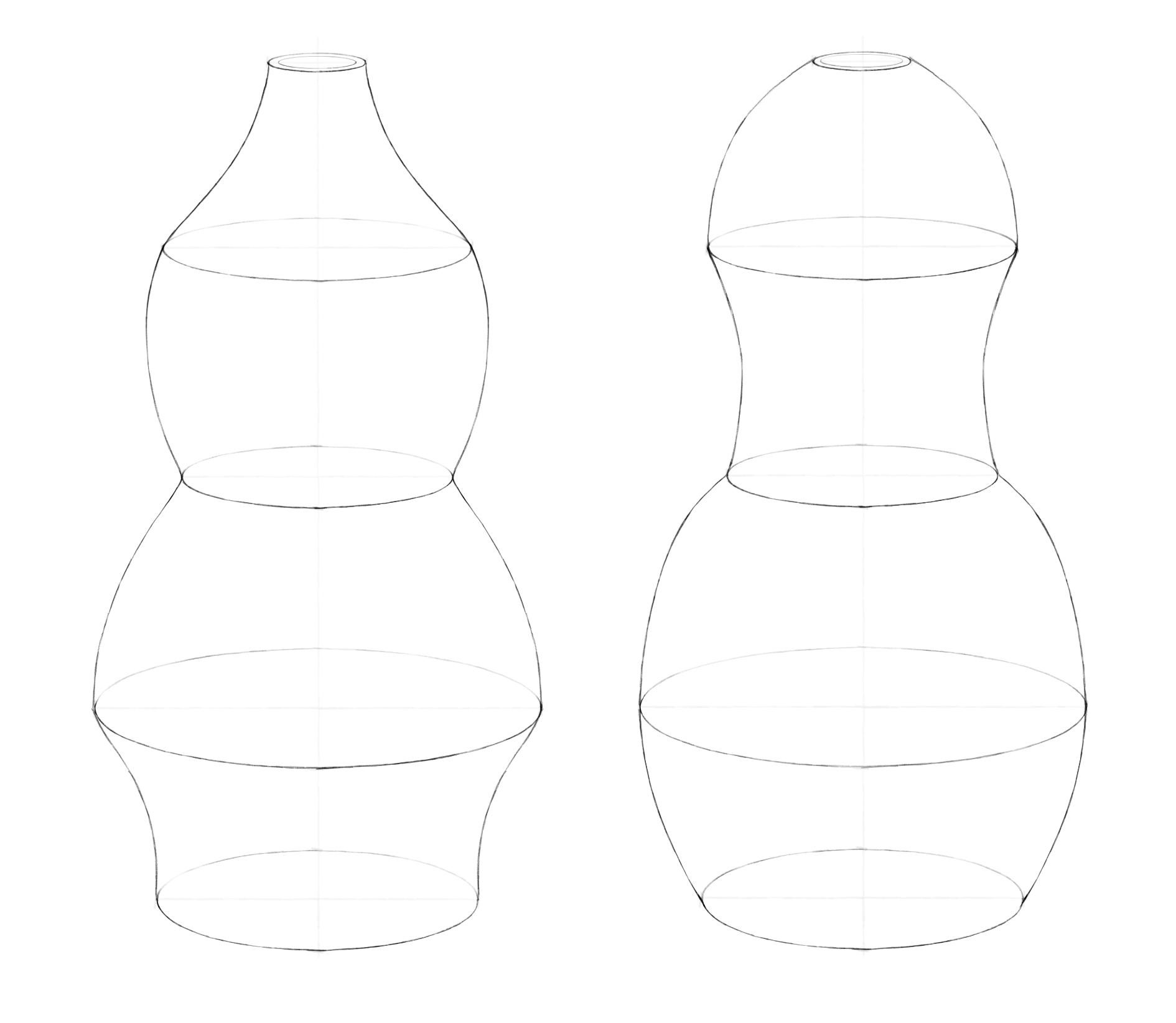
Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.
Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Как правильно нарисовать круг в перспективе, рисуем эллипс
Автор: Юлия · Опубликовано 29.10.2018 · Обновлено 29.10.2018
Те, кто учится в художественных школах и других учебных заведениях, связанных с изобразительным искусством, не понаслышке знают, как не просто рисовать натюрморты с круглыми предметами и гипсовые пособия – цилиндры, конусы, простроенные насквозь шарики. Самое не простое – передать их окружности, повернутые под разным углом в перспективе.
Итак, в этой статье узнаете, как рисовать круг, повернутый в перспективе, правильно с геометрической точки зрения.
Как выглядит круг в перспективе
Запомните: видимая круглая часть предмета, повернутого в перспективе, визуально становится эллипсом. Не сплющенным кругом, не овалом, не бубликом с разными половинками, а именно эллипсом.
Что такое эллипс, можете посмотреть в школьном курсе геометрии. Но для художника важно запомнить его главные черты – симметричность относительно двух перпендикулярных друг другу осей и скругляющиеся по радиусу края. То есть эллипс – абсолютно симметричная фигура.
Есть такая история про разные половинки круга, который повернут под углом в перспективе. Ее рассказывают и в художественных школах и в интернет. Но ее часто истолковывают не верно, что приводит к заблуждению и путанице.
Например, круглая чашка, вид сверху.
Когда мы ее поворачиваем под углом, то сверху мы видим круг уже по-другому. И то, что мы видим, как раз и называется эллипсом.
Запомните раз и навсегда: как бы мы эту чашку не повернули, ее верхушка останется эллипсом. Он может стать шире, уже, но все равно останется эллипсом.
Как нарисовать круг в перспективе с одной точкой схода
Начнем с квадрата, в который впишем круг. В центре пересечения диагоналей квадрата находится и центр круга. Так же через центр проходят оси круга, они перпендикулярны друг другу.
В месте, где оси круга соприкасаются с квадратом, находятся точки касания круга с квадратом. Поэтому оси круга важно изобразить.
Изобразим тот же квадрат в одноточечной перспективе. На пересечение его диагоналей находится центр круга. Через этот центр проходят оси круга.
Можете обратить внимание: ось сместилась, и половинки круга стали не равными. Ближняя половинка круга больше, дальняя – меньше.
Однако, эллипс симметричен. То есть у него обе половинки равные относительно оси. Чтобы найти ось эллипса, делим вертикальную ось круга пополам и проводим через найденную точку еще одну ось. Видим, что данная линия не совпадает с осью круга.
Теперь можно нарисовать эллипс. Делаем его симметричным относительно найденных осей и обрисовываем его, проходя через точки касания.
Как видите, все довольно не сложно. Но мысль о разных половинках круга не дает покоя, мешает нарисовать эллипс ровным и геометрически правильным. Правда, нарисовать ровный эллипс с первого раза не у всех получается, так что не расстраивайтесь, если все равно не выходит. Главное, что Вы рисуете его правильным подходом.
Возникает вопрос: зачем нам тогда рисовать столько линий, обрисовывать квадрат с осями круга и диагоналями? Зачем тогда все усложнять? Предположим, что мы рисуем сахарницу с крышкой сверху. У крышки есть ручка в центре. Когда мы смотрим на нее под углом, то ручка будет визуально смещаться, то есть располагаться в центре круга. Центр круга находится на пересечение диагоналей, как мы выяснили, то есть со смещением относительно центра эллипса.
Когда Вы рисуете какой-нибудь сложный предмет, например, балясину, нахождение центра круга Вам будет необходимо. Это поможет разместить отдельные элементы конструкции на одной оси.
Как нарисовать цилиндр
В перспективе с одной точкой схода все просто. Но если мы рисуем объект с двумя точками схода, то все может быть сложнее. Например, возьмем цилиндр, лежащий на боку.
Самый частый вариант исполнения без правильного построения – это сплющенный цилиндр. Он получается не круглым, а смотрится приплюснутым.
В учебном рисунке все сложные формы следует представлять в виде более простых фигур. Представим наш цилиндр в виде параллелепипеда, обрисованного по точкам касания с цилиндром.
Главное, правильно определить направление граней этого параллелепипеда и достоверно отобразить перспективу. Когда рисуем цилиндр с натуры, то смотрим угол меду двумя гранями.
Как и в случае с одноточечной перспективой, центр круга находится на пересечение диагоналей квадрата. Через найденный центр проводим оси круга.
Чтобы найти оси эллипса, нам нужно найти ось вращения цилиндра. Для этого строим параллелепипед насквозь и проводим ось вращения от центра передней грани к центру задней грани.
Найдем малую ось эллипса – она всегда параллельна оси вращения и находится на середине оси круга. В перспективе с двумя точками схода эта середина часто совпадает с центром круга (или почти совпадает, как у меня), но не всегда.
Рисуем малую ось эллипса. Большая ось перпендикулярна малой. Главное следить за тем, чтобы оси были перпендикулярны друг другу.
Обозначим точки касания и, проходя через них, рисуем симметричный эллипс. Чтобы не получилось криво, следим за отрезками эллипса по осям – они должны быть одинаковые.
Иногда случаются не состыковки, никак не получается ровно пройти через все точки касания, так сказать натянуть эллипс на точки касания. Во-первых, проверьте квадрат – он может быть у Вас слишком сильно, неестественно уведен в перспективу, или наоборот, перспектива отсутствует. Во-вторых, не ловите миллиметры, их все равно в рисунке никто никогда не увидит, если сам Ваш эллипс выглядит ровным и убедительным.
Задняя часть цилиндра рисуется аналогичным образом.
Можно заметить, что дальний эллипс выглядит шире и круглее, чем передний. Это значит, что перспективу мы нарисовали верно, потому что заднюю часть мы видим как бы больше, чем переднюю. Отсюда такой эффект. Возможно, у меня довольно грубовато все нарисовано, не совсем все идеально ровно, но главное – передать суть.
И теперь можно завершить рисунок цилиндра.
Как вписать круги в грани куба
Это волшебное упражнение поможет Вам научиться рисовать круги в любых поворотах при любой перспективе. Рисуем куб и вписываем в его грани круги.
Верхняя грань:
Прорисовываем кубик насквозь и на верхней грани рисуем диагонали и оси.
Мы нашли четыре точки касания. Малая ось эллипса у нас расположена строго вертикально. Большая перпендикулярна ей.
Аналогичным способом вписываем круг в переднюю грань. Диагонали, линия середины, точки касания. Обрисовываем эллипс, проходя через точки касания и симметрично относительно осей.
Таким же образом вписываем круг в последнюю грань.
И самое главное: Вы должны понимать, что рисунок – это не точная наука, не геометрия. И не надо зацикливаться на ловле миллиметров, все стирать и перерисовывать заново, если что-то не состыковывается в геометрическом плане. Задача художника не в том, чтобы нарисовать геометрически точно, а в том, чтобы его рисунок был убедительным. Это особенно актуально, когда дело касается геометрически правильных фигур.
Итак, при рисовании кругов в перспективе правильно прикидывайте направление осей эллипса и старайтесь нарисовать эллипс симметричным относительно этих осей. И не надо ловить миллиметры.
Учимся рисовать эллипс и цилиндр в перспективе.
Как выглядит цилиндр в перспективе?
Поместим на стол круглую банку из-под кофе и чертежный тубус.
Верх и дно этих цилиндров представляют собой круги.
Закройте один глаз. Держите эту картинку (картинка на бумаге) правым краем к себе и смотрите на эллипс в направлении, указанном стрелкой. В таком положении эллипс выглядит кругом, а круг кажется эллипсом.
Так мы обнаруживаем, что, когда мы смотрим на круг сбоку, он выглядит как эллипс.
На иллюстрации вверху показан круг, вписанный в квадрат, и тот же самый круг, вписанный в квадрат, но изображенный в перспективе.
Круг, нарисованный с применением перспективы, превращается в эллипс.
Торцы цилиндра, нарисованного в перспективе, принимают овальную форму.
Рисуем эллипс от руки.
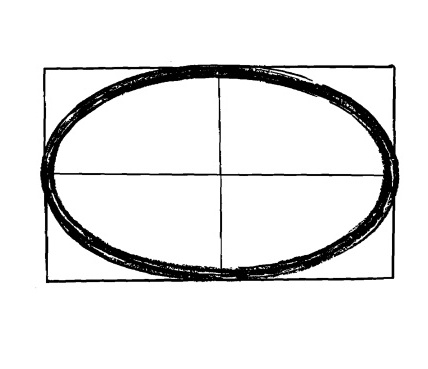
Нарисуйте прямоугольник, длина и ширина которого соответствуют нужным вам длине и ширине эллипса. Эллипс будет касаться контуров прямоугольника в центральной точке каждой из сторон.
Попрактикуйтесь рисовать эллипс от руки, используя прямоугольник как основу. Удивительно, как при некоторой практике нарисованный от руки эллипс будет совпадать с тем же самым эллипсом, вычерченным с применением вспомогательных инструментов.
Элементы черчения для начинающих — построение эллипса техническими способами.
Первый способ начертить эллипс.
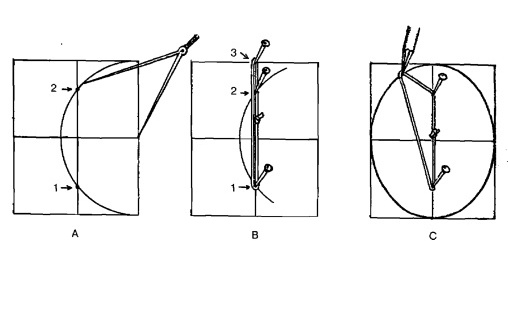
Давайте начертим эллипс, вписанный в прямоугольник А.
Сначала при помощи циркуля найдите, где круг (показанный на рисунке А) пересекает длинную среднюю линию. Эти пересечения обозначены точками (1) и (2).
Воткните в эти точки булавки, а третью булавку (3) — в конце средней линии.
Крепко обвяжите эти булавки прочной льняной ниткой, как показано на рисунке В.
Удалите булавку (3) и очертите карандашом эллипс, как показано на рисунке С. Нитка должна быть постоянно равномерно натянута.
Второй способ построения.
Вот еще один способ как начертить эллипс, вписанный в прямоугольник А.
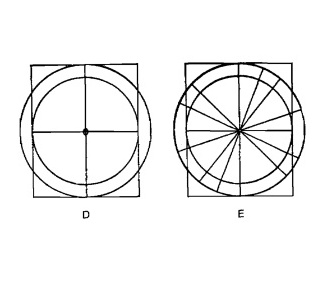
Начертите два круга с центром в точке О. Диаметр одного круга должен быть равен ширине прямоугольника, а диаметр другого — длине прямоугольника, как показано на рисунке D.
Теперь проведите линии наподобие спиц колеса, как показано на рисунке Е.
Через точки пересечения спиц с малым кругом проведите линии, параллельные длинным сторонам. Через точки пересечения спиц с большим кругом проведите линии, параллельные коротким сторонам.
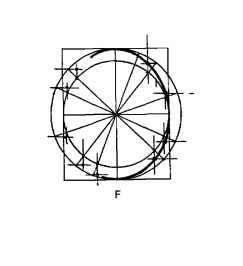
Эллипс проходит через точки пересечения линий, параллельных коротким сторонам и параллельных длинным сторонам, как показано на рисунке F.
Третий способ построения эллипса.
Приводим еще один способ начертить эллипс определенной величины.
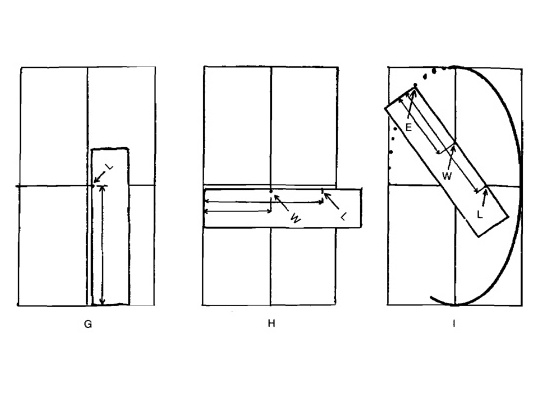
Возьмите полоску бумаги и отметьте на ней половину длины данного в качестве основы прямоугольника. Обозначьте точку буквой L, как показано на рисунке G.
Далее положите полоску вдоль линии ширины и буквой W обозначьте точку, отмечающую половину этой ширины, как показано на рисунке Н.
Теперь поместите бумажную полоску так, чтобы точка L касалась линии ширины, а точка W касалась линии длины, как показано на рисунке I.
Кончик полоски (обозначенный буквой Е) показывает, где проходит контур эллипса.
Продолжайте двигать полоску по кругу, пока не отметите столько точек, сколько вам нужно.
Этот метод подходит для вычерчивания эллипсов любой величины. При черчении после обозначения точек можно вычертить контур эллипса по лекалу.
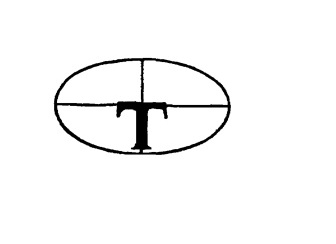
Длинные и короткие оси эллипса.
Самая длинная линия, пересекающая эллипс, называется длинной осью.
Самая короткая линия, пересекающая эллипс, называется короткой осью.
В месте своего пересечения длинная и короткая оси образуют прямые углы. Будем считать, что длинная ось образует поперечную перекладину буквы T, а короткая ось — ножку буквы T.
Это соотношение между осями и буквой T остается истинным вне зависимости от размера, конфигурации или положения эллипса.
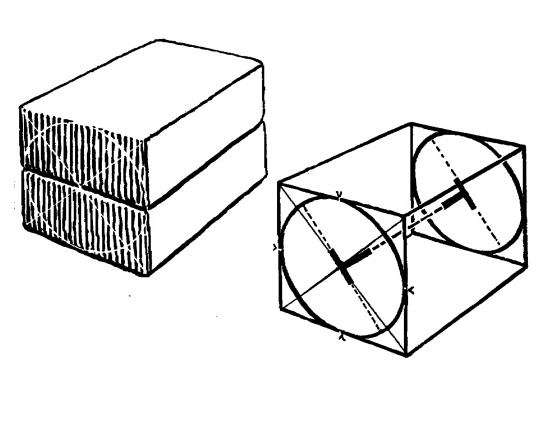
Построение цилиндра в перспективе, вид сбоку.
Положим один кирпич поверх другого. Предположим, что их торцы образуют квадрат. Нарисуем на торцах диагонали и тем самым найдем центр. Это центр круга, который касается всех четырех сторон квадрата.
Этот круг можно расценивать как торец цилиндра, который проходит через всю толщу кирпича. На противоположном торце нарисуем еще один круг.
Длинная ось образует перекладину буквы Т.
Мы начали с предположения, что торцы двух кирпичей, положенных один на другой, образуют квадрат.
Теперь попробуем рисовать цилиндр в перспективе.
Нарисуем кирпичи с применением законов перспективы. Круг, вписанный в квадрат, становится эллипсом, касающимся сторон квадрата (нарисованного в перспективе) в центре каждой из сторон.
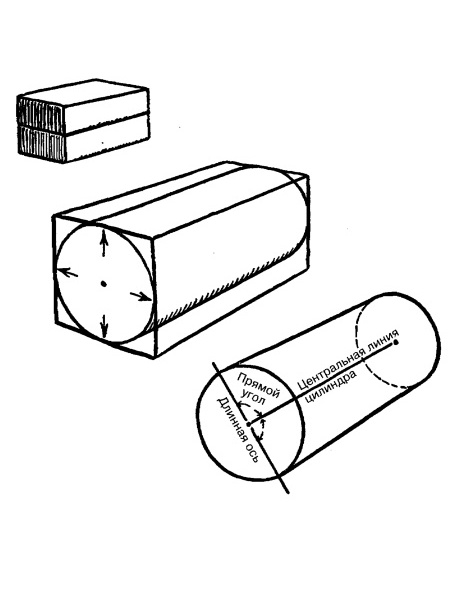
Рис. 13.12. Построение цилиндра в перспективе.
Линия, проведенная через центр круга до точки схода, должна быть центральной линией цилиндра или осью для двух колес.
Линия, проведенная через этот же центр и пересекающая эту ось под прямым углом, будет самой длинной линией или большой осью эллипса.
Большая ось всегда образует прямой угол с центральной осью цилиндра.
Нет никакой разницы, в каком направлении лежит цилиндр и лежит ли он на боку или стоит на торце, большая ось эллипса всегда будет образовывать букву Т с центральной/осевой линией цилиндра. Малая ось эллипса лежит вдоль этой центральной/осевой линии цилиндра. Малая ось эллипса становится центральной линией цилиндра, т.е. они должны совпадать.
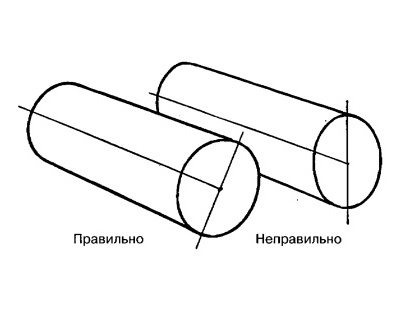
Рис. 13.13 . Правильное положение осей эллипса цилиндра в пространстве.
Нарисуйте/начертите цилиндр с соблюдением правил перспективы. Затем поверните бумагу так, чтобы цилиндр оказался в вертикальном положении.
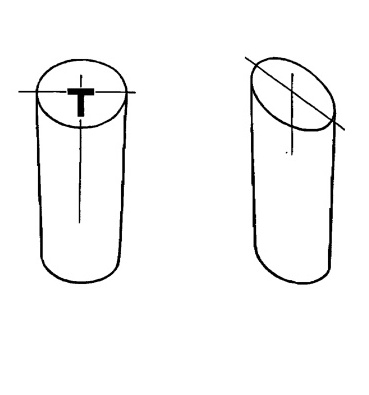
Рис. 13.14 . Цилиндр в перспективе в вертикальном положении.
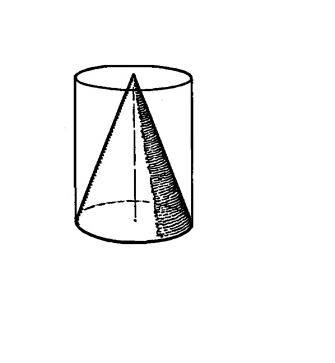
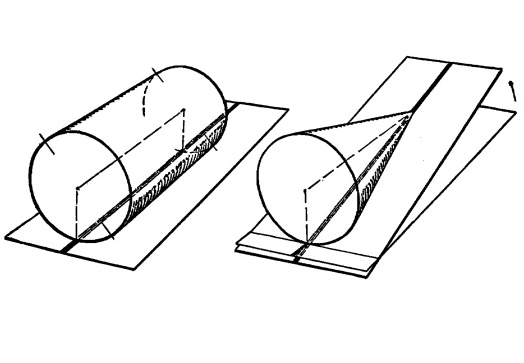
Рисуем конус, лежащий на боку.
Конус можно сделать из цилиндра, как показано на рисунке.
Теперь мы будем рисовать конус, лежащий на боку.
Сначала рисуем цилиндр, лежащий на боку вдоль черной линии, как показано на рисунке.
Затем из цилиндра, лежащего в этом положении, делаем конус.
Мы хотим разместить конус так, чтобы он лежал на плоской поверхности. Чтобы сделать это, мы наклонно приподнимаем поверхность так, чтобы она оказалась прижата к конусу. Верхушка конуса теперь лежит на черной линии.
Теперь давайте расположим всю композицию так, чтобы поверхность снова была горизонтальной, а конус оставался лежать на ней.
Таким образом, конус можно считать цилиндром, один торец которого на половину своего диаметра вдавлен в поверхность, на которой он лежит. Затем из этого цилиндра делается конус.
Основные выводы тринадцатого урока.
Круг, нарисованный в перспективе, выглядит как эллипс.
Цилиндр, нарисованный в перспективе, можно рассматривать как два колеса, ось которых образована центральной линией.
Длинная ось эллипса образует перекладину буквы Т с центральной линией.