Как построить диметрическую проекцию конуса
Как построить диметрическую проекцию конуса
§ 13. Построение аксонометрических проекций
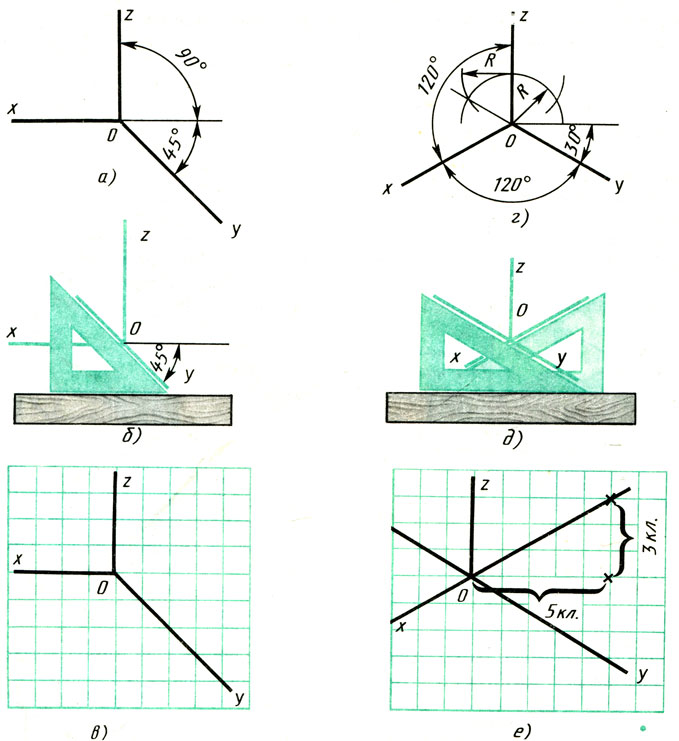
Построение аксонометрических проекций начинают с проведения аксонометрических осей.
Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 85, б.
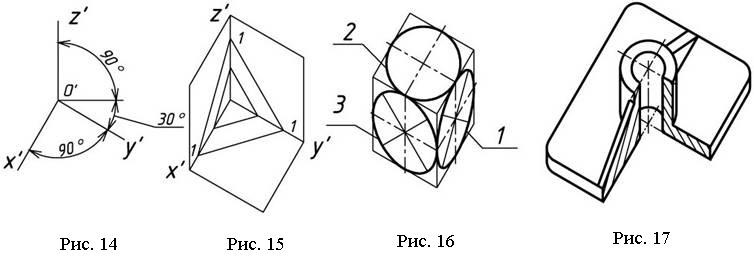
Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 85, д).
Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.
При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название «диметрия», что по-гречески означает «двойное измерение».
При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».
На рис. 85, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток).
Рис. 85. Способы построения осей аксонометрических проекций
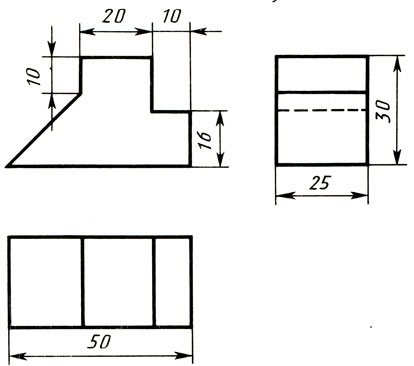
Построение фронтальной диметрической и изометрической проекций. Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 86.
Рис. 86. Комплексный чертеж детали
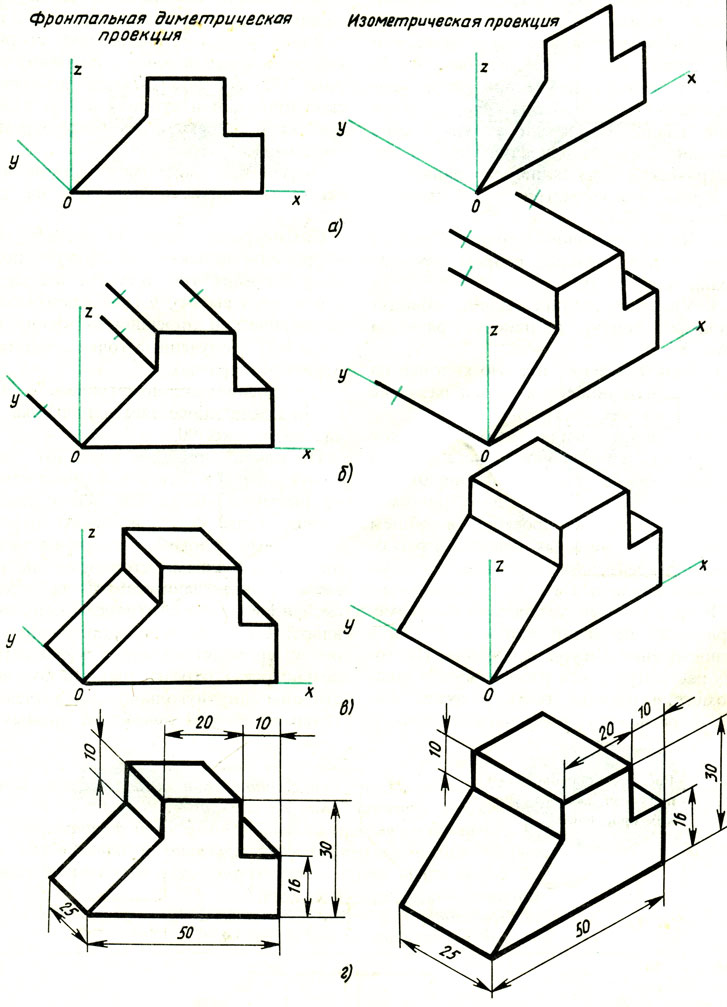
Порядок построения проекций следующий (рис. 87):
3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 87, в).
4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 87, г).
Сравните левую и правую колонки на рис. 87. Что общего и в чем различие данных на них построений?
Рис. 87. Способ построения аксонометрических проекций
Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.
В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.
Построение аксонометрической проекции квадрата показано на рис. 88, а и б.
Построение аксонометрической проекции треугольника показано на рис. 89, а и б.
Построение аксонометрической проекции правильного шестиугольника показано на рис. 90.
По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.
Ответьте на вопросы
1. Как располагают оси фронтальной диметрической и изометрической проекций? Как их строят?
2. Какие размеры откладывают вдоль осей фронтальной диметрической и изометрической проекций и параллельно им?
3. Вдоль какой аксонометрической оси откладывают размер уходящих вдоль ребер предмета?
4. Назовите общие для фронтальной диметрической и изометрической проекций этапы построения.
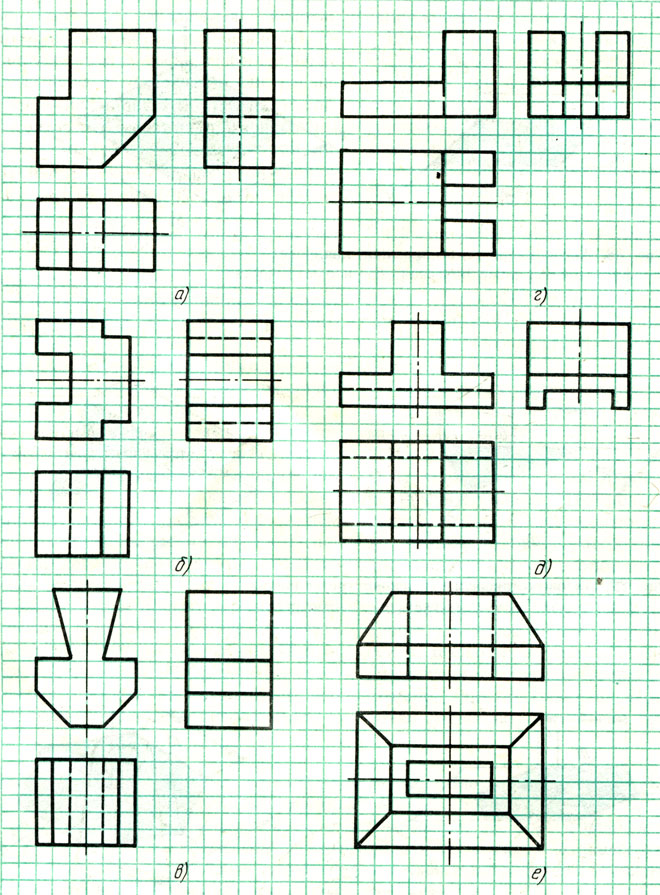
Задания к § 13
Упражнение 40
Размеры определите по числу клеток, считая, что сторона клетки равна 5 мм.
В ответах дано по одному примеру последовательности выполнения заданий.
Рис. 91. За типе на построение аксонометрических проекций
Упражнение 41
Постройте в изометрической проекции правильные четырехугольную, треугольную и шестиугольную призмы. Основания призм расположены горизонтально, длина сторон основания 30 мм, высота 70 мм.
В ответах дан пример последовательности выполнения задания.
Как построить диметрическую проекцию конуса
Аксонометрические проекции применяются в качестве вспомогательных к чертежам в тех случаях, когда требуется поясняющее наглядное изображение формы детали. В ГОСТ 2.317-69 стандартизованы прямоугольные и косоугольные аксонометрические проекции с различным расположением осей.
ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ
Изометрическая проекция
Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям. Для изометрической проекции вариант штриховки по плоскостям приведен на рис. 2.
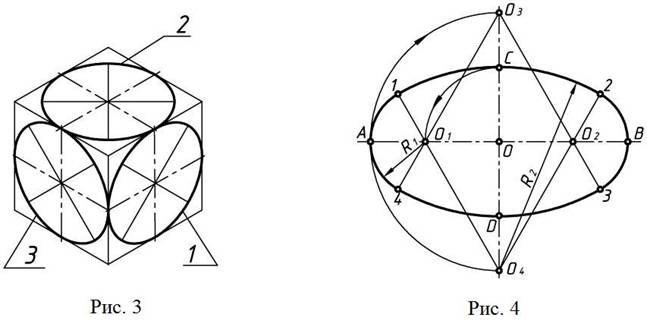
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 3).
Построение эллипсов в изометрической проекции окружности можно заменить построением овалов, Следует отметить, что очертание любого циркульного овала не совпадает с очертанием эллипса, имеющего такие же оси, хотя и приближается к нему. Один из способов построения овала приведен на рис. 4.
Пример изображения детали в прямоугольной изометрии приведен на рис. 5.
Диметрическая проекция
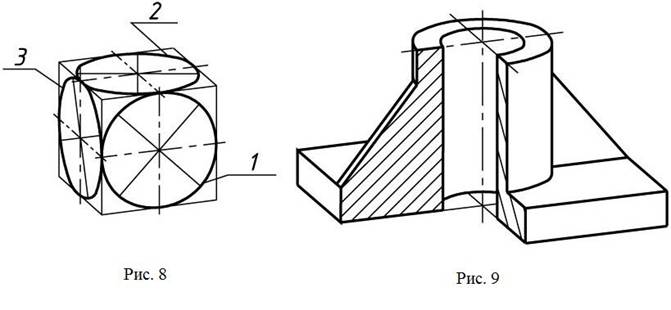
Штриховка сечений в прямоугольной диметрической проекции показана на рис.7, а пример изображения детали – на рис. 9.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 8).
КОСОУГОЛЬНЫЕ ПРОЕКЦИИ
Фронтальная изометрическая проекция
Штриховка сечений в косоугольной фронтальной изометрической проекции показана на рис. 11, а пример выполнения изображения детали – на рис.13.
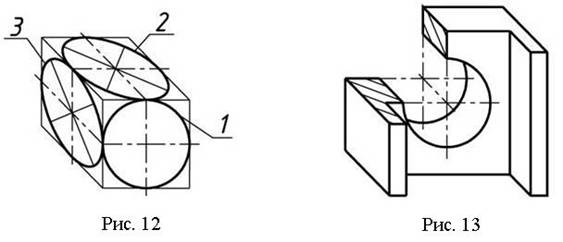
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис. 12).
Горизонтальная изометрическая проекция
Штриховка сечений в косоугольной горизонтальной изометрической проекции показана на рис.15, а пример изображения детали – на рис. 17.
Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций, – в эллипсы (рис.16).
Фронтальная диметрическая проекция
Штриховка сечений в косоугольной фронтальной диметрии показана на рис.19, а пример изображения детали – на рис.21
Аксонометрические проекции
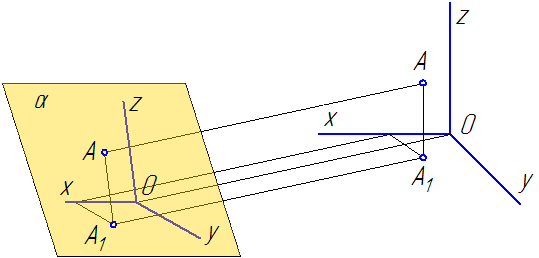
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).
Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
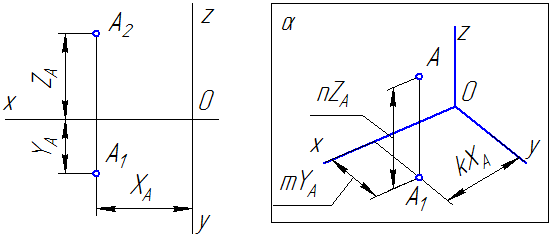
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.
Рисунок 4.2
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:
Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.
4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.
Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.
Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции
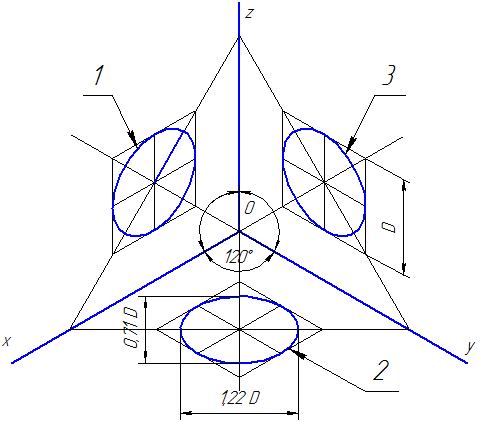
4.1.2. Диметрическая проекция
Положение аксонометрических осей проводится на Рисунке 4.5.
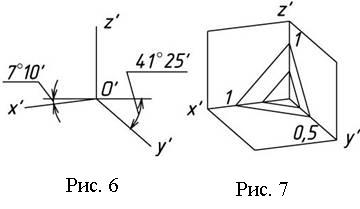
Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
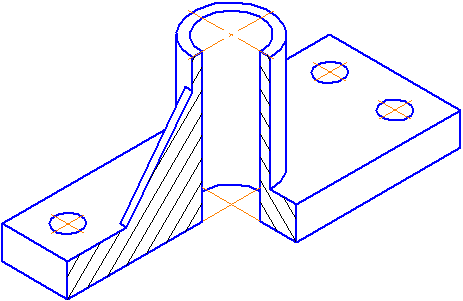
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.
Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции
Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции
4.2 Косоугольные проекции
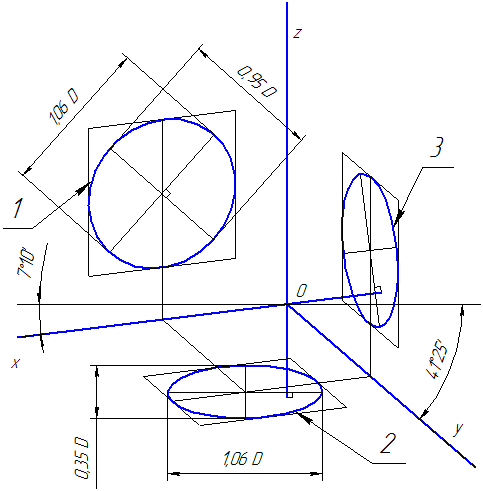
4.2.1 Фронтальная диметрическая проекция
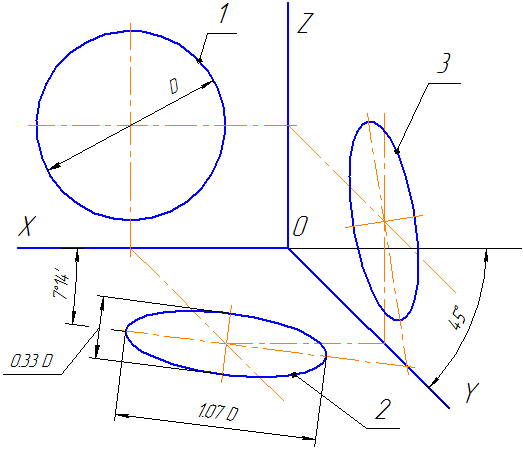
Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.
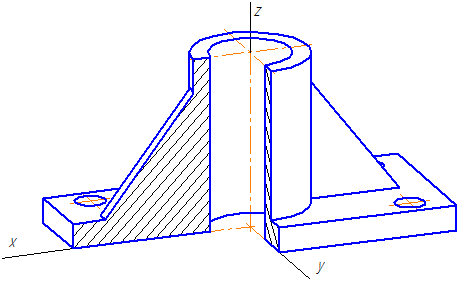
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.
Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
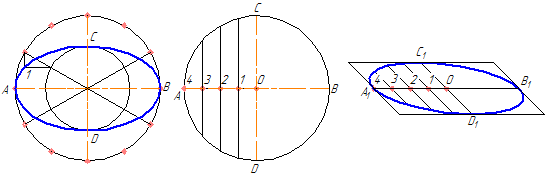
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из этих окружностей делится на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).
4.4 Штриховка сечений
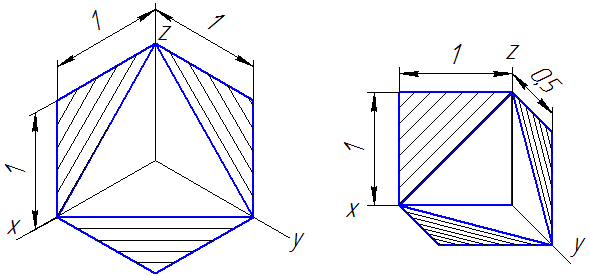
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).
а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях
Как построить диметрическую проекцию конуса

Как построить диметрию детали?
Пять лет назад я написал урок на тему «Как построить изометрию?». Я знал, что пишу очень нужную статью, что такого подробного описания в сети просто нет. Но я и подумать не мог, что этот урок станет бестселлером. Каждый год к нему обращаются более 40 тысяч студентов, и я точно знаю, что не меньше трети из них обретают умение или, как минимум, перестают шарахаться от изометрии как от огня и начинают понимать, с какого бока к ней вообще надо подходить. И в том числе поэтому я крайне не рекомендую браться за урок построение диметрии если построение изометрии является для вас чем-то немыслимым. Дело в том, что в статье «построение изометрии детали» я очень подробно разобрал некоторые моменты, связанные с осями, их приложением к детали, и прочие нюансы, которые уже не будут так тщательно разобраны здесь.
При этом, как указано на рисунке, расстояния откладываемые вдоль осей X и Z откладываются без искажений (с приведенным коэффициентом 1), а расстояния вдоль оси Y откладываются с коэффициентом 0.5, т.е. уменьшаются в два раза. Благодаря такому расположению осей и линейным коэффициентам диметрия значительно эффективнее раскрывает наглядный вид деталей, в конструкции которых имеются четырех- и шестиугольные призмы. Кроме того, диметрия несколько экономичнее изометрии в плане занимаемого на листе пространства, но наверное актуальность этого уже в прошлом.
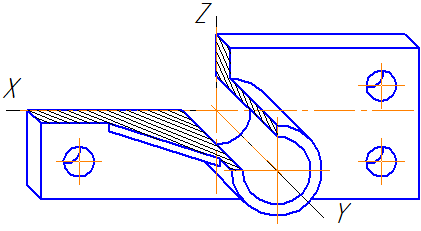
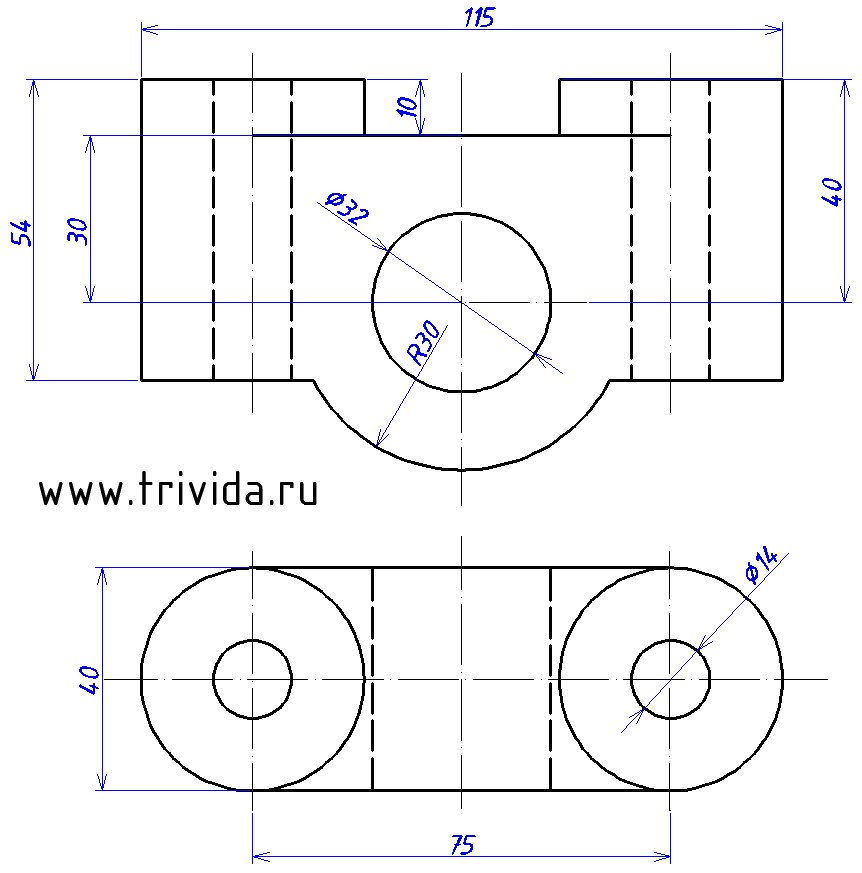
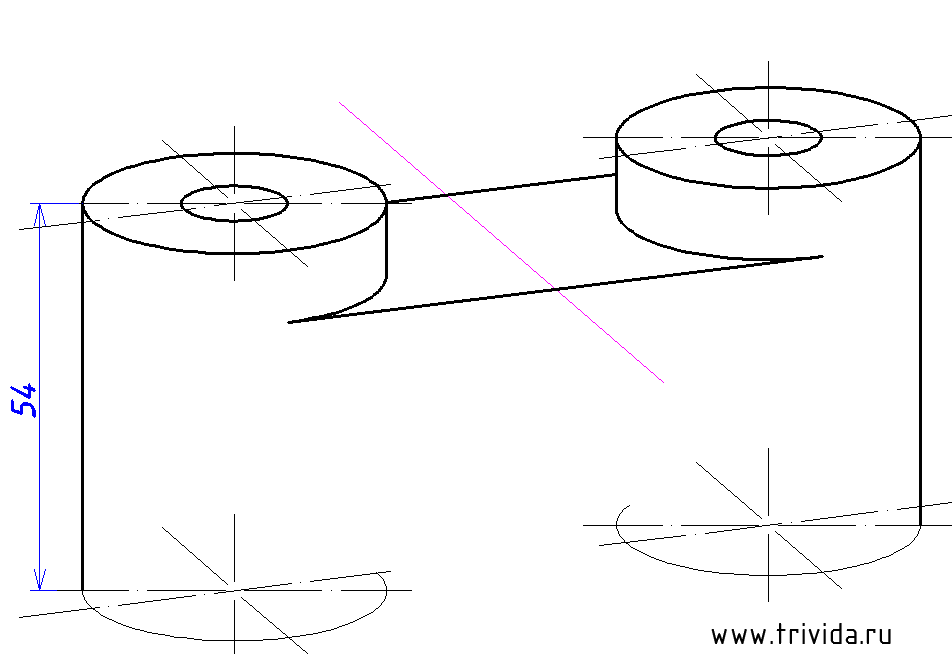
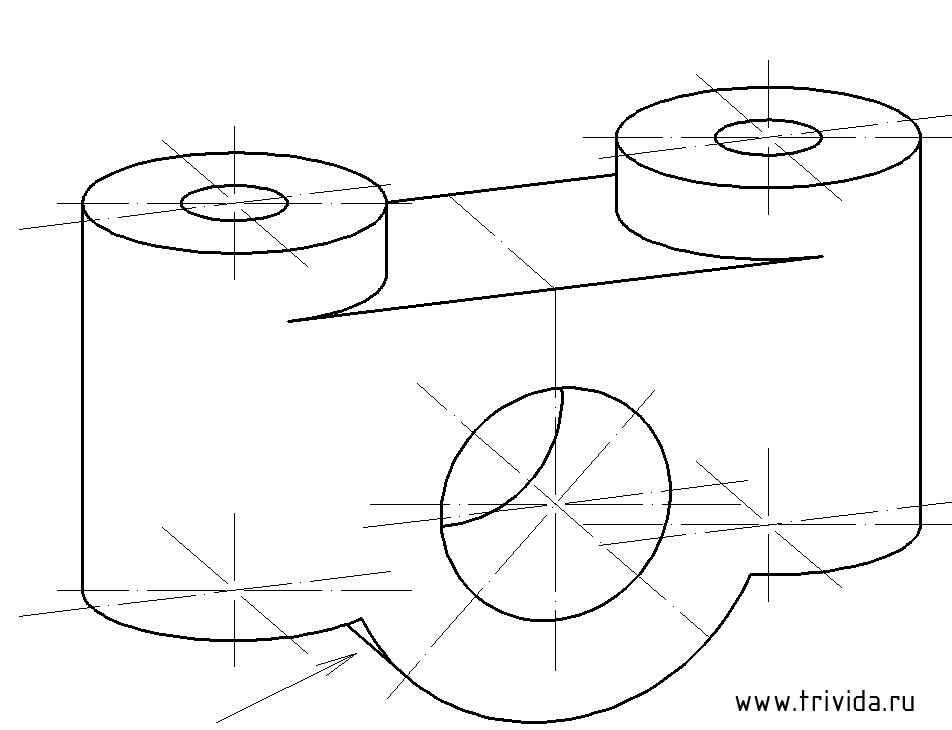
Итак, мы получили задание начертить диметрию вот такой детали. Ее можно описать как нечто похожее на бинокль, но вместо колесика для наведения резкости тут мы имеем сквозное отверстие диаметром 32мм. Сложно? В меру. Не совсем просто, но и не слишком накручено. То, что надо.
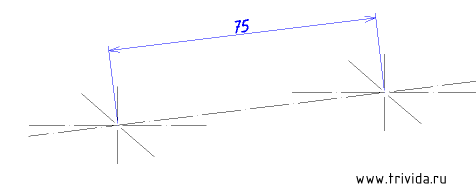
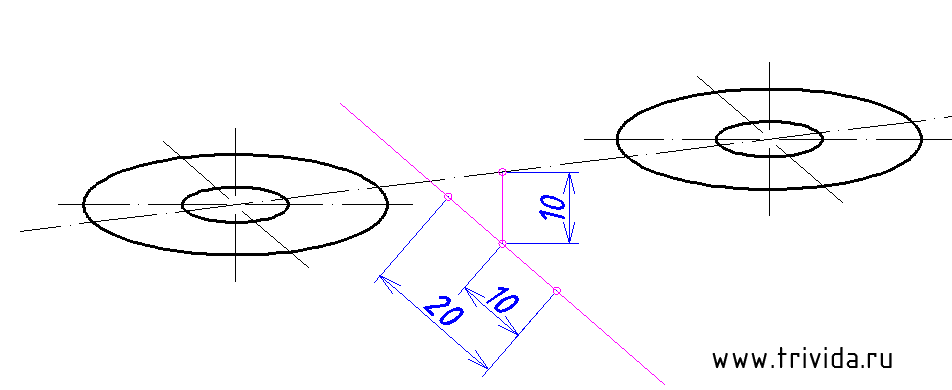
Воспользовавшись указанным способом построим два центра для наших будущих «окуляров». Они должны быть на расстоянии 75 мм отложенных вдоль оси X. (По сути нужно построить один центр по указанной технологии, затем отложить 75мм и через полученную точку провести оси, параллельные исходным)
Внимание: я не расписываю подробно, как построить красивый эллипс, зная две его оси. Этому у меня посвящен отдельный урок: как построить эллипс. Не совсем наш случай, но очень в тему еще один урок: «как начертить окружность в изометрии». Впрочем, если вы добрались до изучения диметрии, вы уже должны иметь представление о построении эллипсов.
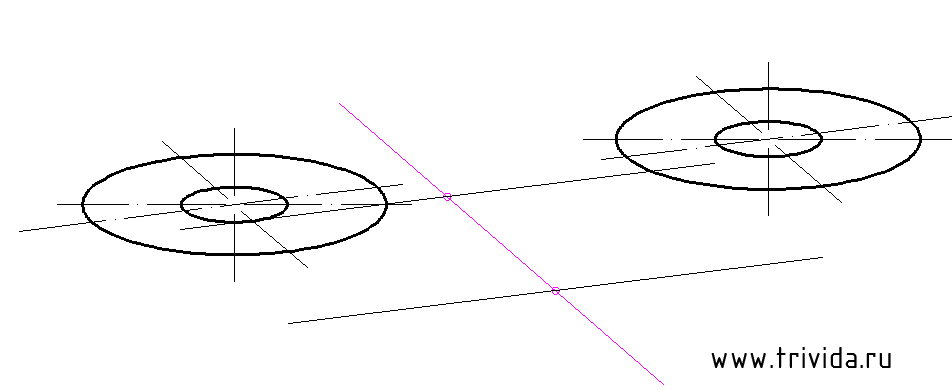
Согласно исходному чертежу наши «окуляры» на 10мм возвышаются над горизонтальной площадкой. Центр этой площадки расположен на 10 мм ниже середины отрезка, соединяющего центры наших эллипсов. А отложив по 10мм (почему не по 20? Потому что коэффициент 0.5, не забываем! )в каждую сторону вдоль оси Y, мы получим засечки, которые помогут нам прочертить границы этой горизонтальной площадки:
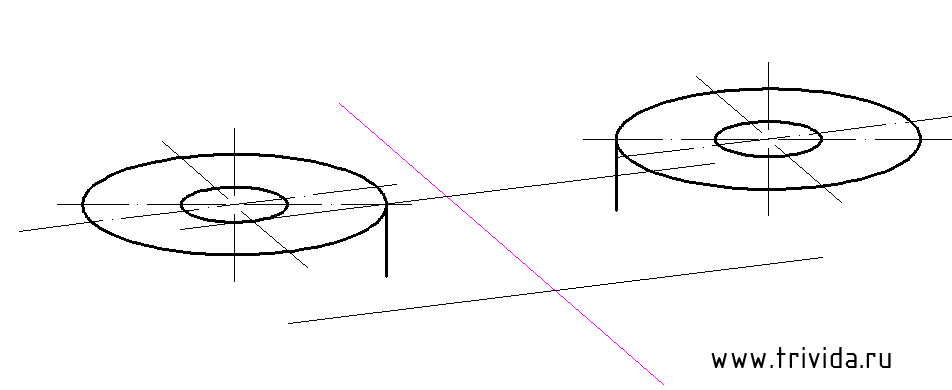
И, собственно, сами границы:
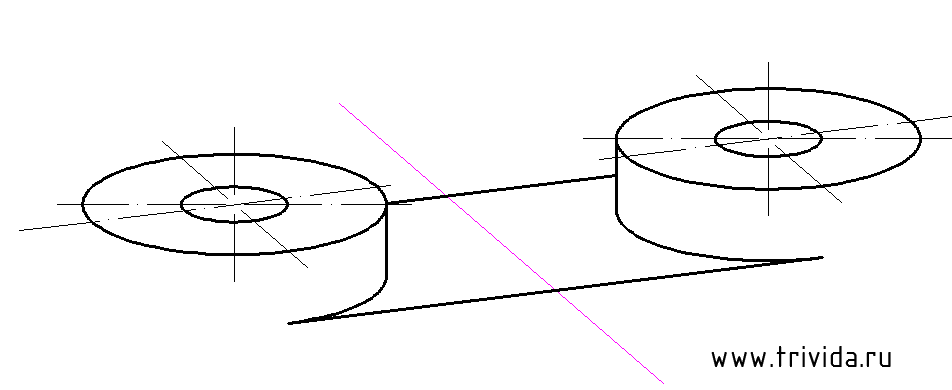
Теперь опустим вертикальные отрезки по 10мм от крайних точек больших эллипсов:
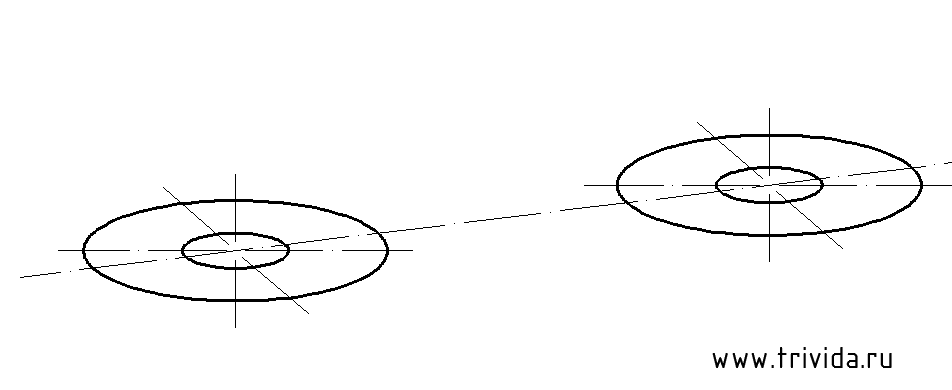
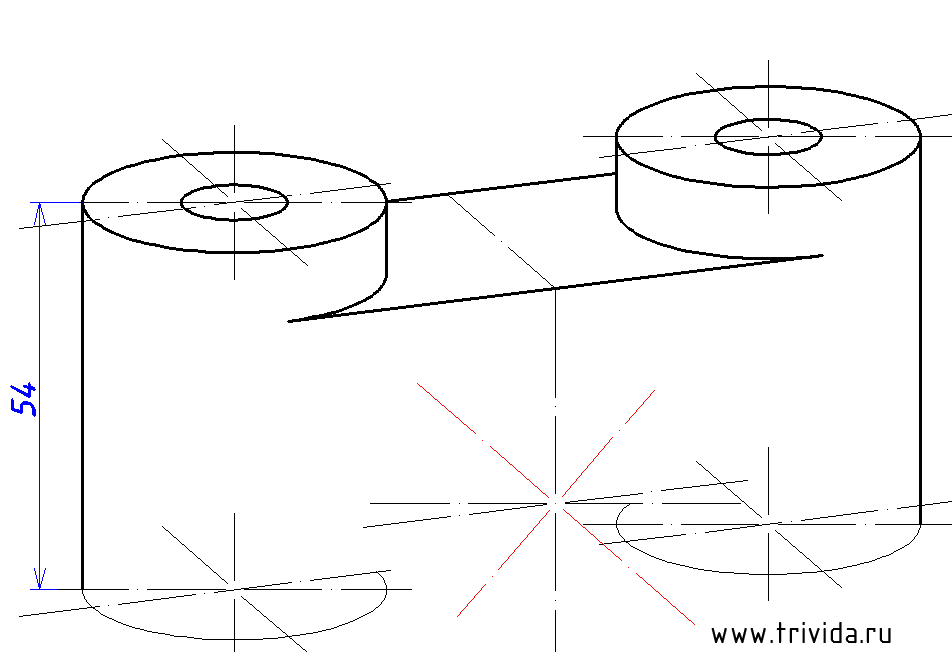
Строим центры нижних окружностей «окуляров». Они будут на 54мм ниже верхних центров. Кроме того, мы можем сразу провести крайние вертикальные боковые границы. Сами эллипсы строим или переносим, но пока в тонких линиях:
Пришло время заняться центральным отверстием. В отличии от уже построенных, центральная окружность лежит в другой плоскости, осью вращения в которой является ось Y. Ничего страшного нет, но нужно учесть два момента:
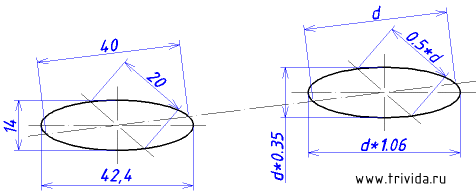
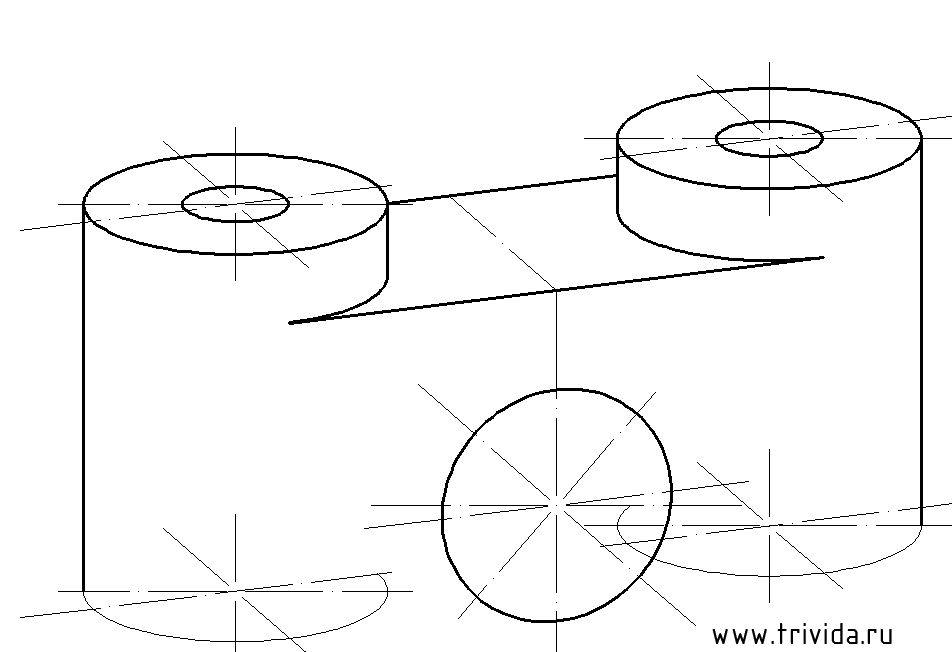
1. Большая ось эллипса будет перпендикулярна оси Y (такой оси мы сегодня еще не обозначали, это новое направление. Чтобы ни с чем не перепутать, оси данного эллипса я обозначил на рисунке красным цветом). Центр будет располагаться на 30 мм ниже горизонтальной площадки:
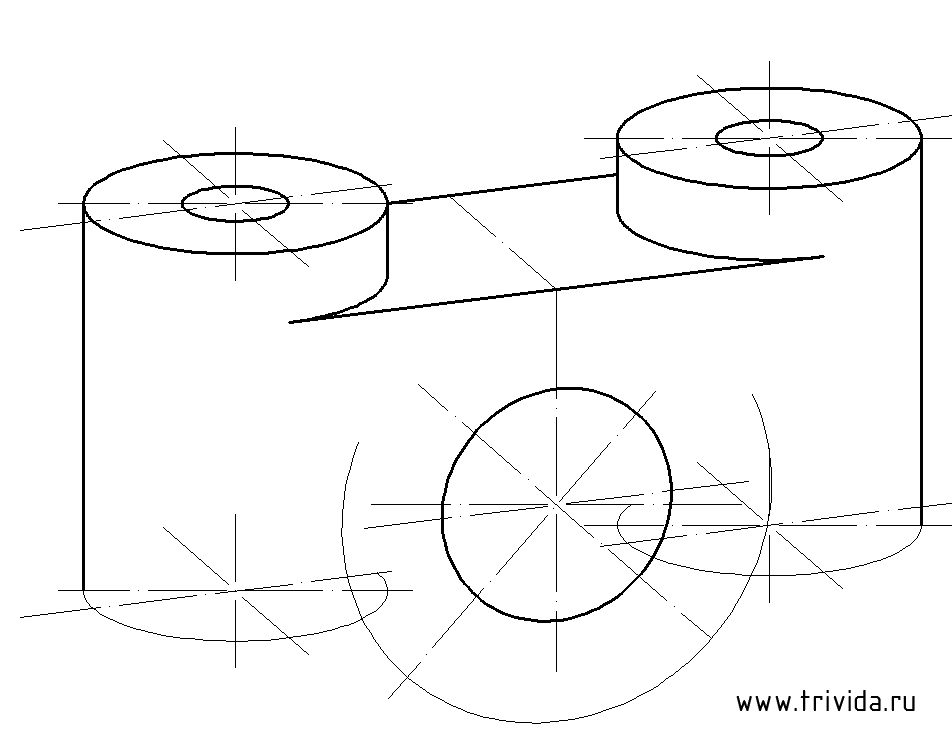
Остается построить еще один аналогичный эллипс с тем же центром. Исходные данные: диаметр 60мм, большая ось 63,6мм малая ось 57мм
Обозначив набросками наш последний эллипс, обводим его видимую часть, а так же ранее обозначенные нижние границы «окуляров» и стираем лишнее. Так же для приличия проведем отрезок, обозначающий границу цилиндрической поверхности (указан стрелкой). Возможно, про него никто бы и не вспомнил, но он есть, нужно прочертить:
Обратите внимание, у центрального отверстия появилась дальняя граница. Это копия эллипса, смещенная на 20мм вдоль оси Y. (Ширина детали 40мм, коэффициент по оси Y равен 0.5)
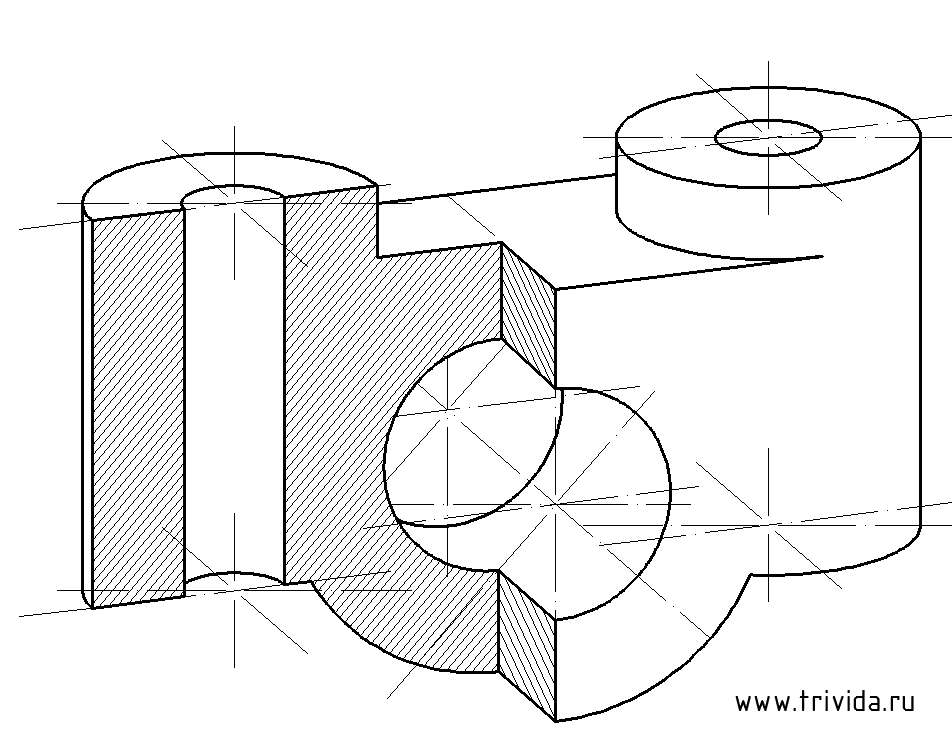
По сути, на этом наш урок «пошаговое построение диметрии» закончен. Однако, было бы неправильным, лишить вас самого интересного, и не отрезать четвертушку 🙂 Да, это потребуется не каждому, но зато для тех, кому придется данную процедуру выполнять, следующая картинка даст хороший наглядный материал, и наверняка поможет в неравной борьбе с домашним заданием:
Вот, теперь все. Ничего нового сюда уже не добавить. Если на вашей кафедре требуют, то в свободной зоне нужно вычертить и обозначить оси (направления, углы, названия), а в случае с вырезом четверти, не помешает и обозначение направления штриховки (в данном уроке не разбирается, но там ничего сложного, практически копия самой первой картинки в уроке).
До встречи на новых уроках!
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
Автор комментария: Vv
Дата: 2015-11-20
Большое спасибо, добрый человек!
Все-таки приятно, когда тебя называют добрым без сарказма!
Автор комментария: Роман
Дата: 2015-12-24
Очень полезно. Спасибо автору.
Автор комментария: Кир
Дата: 2016-04-01
Автор комментария: ивангай
Дата: 2016-11-21
Приветствую! Начните с урока про изометрию. Без этого у вас нет шансов. К сожалению это очень сложный материал, на него нельзя запрыгнуть на ходу.
Автор комментария: Юлия
Дата: 2017-05-02
Добрый день. Спасибо за урок (тут даже разрез сделан). Он очень полезен. Не нашла правда тут материала по построению триметрии. Будет ли?
Автор комментария: Юлия
Дата: 2017-05-02
Добрый день. Спасибо за урок (тут даже разрез сделан). Он очень полезен. Не нашла правда тут материала по построению триметрии. Будет ли?
Автор комментария: Александр
Дата: 2018-11-22
Статья полезная,но верхний чертёж начерчен неточно: не указана линия пересечения нижней центральной цилиндрической поверхности с нижней плоскостью.
Добавьте свой комментарий:
Наша страница в ВК:
Антон, у вас офис только в Москве? или в других городах тоже есть?