Как построить диаграмму в маткаде

Как построить диаграмму в маткаде

Построение графиков в Mathcad

Для построения графиков в Mathcad можно воспользоваться функцией Вставка > График > Тип графика или панелью инструментов График (рис. 1.11). Поддерживаются следующие типы графиков:

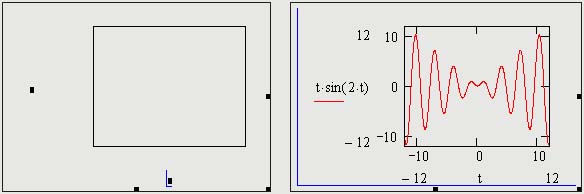
При выборе режима построения двумерного графика в координатных осях Х-У на рабоче листе создается шаблон (на рис. 1.12 слева) с полями-заполнителями для задания отображаемых данных по осям абсцисс и ординат (имена аргументов и функций или выражения для них, а также диапазоны изменения значений). Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Заполнители для граничных значений появляются после ввода аргумента и/или функции. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменения величин, но их можно задать, щелкнув в области соответствующих полей-заполнителей и изменив значения в них.

В правом фрагменте рис. 1.12 показан заполненный параметрами шаблон, причем диапазоны значений по осям определены вручную. Отметим, что эти значения видны только в режиме редактирования графика (наличие углового курсора на рисунках свидетельствует, что блок с графиком в данный момент выделен).

По оси абсцисс можно отложить простую переменную, задав для нее граничные значения (как на рис. 1.12), диапазон (о формировании диапазонов см. раздел «Работа с матрицами»), вектор значений. В заполнителях у оси ординат обычно помещают функции, выражения или векторы. На рис. 1.13 значения аргументов и трех функций размещены в столбцах двумерной ьатрицы. На графике отображены значения элементов из соответствующих столбцов.

В одной графической области можно построить несколько графиков. Для этого надо у соответствующей оси перечислить несколько выражений через запятую (см. рис. 1.13).

Аналогичным образом строится и форматируется график в полярных координатах, а для графиков других типов предварительно следует создать матрицы значений координат точек.

Для построения простейшего трехмерного графика, необходимо задать матрицу значений. Отобразить эту матрицу можно в виде поверхности, столбчатой диаграммы или линий уровня. Для отображения векторного поля значения матрицы должны быть комплексными. В этом случае в каждой точке графика отображается вектор с координатами, равными действительной и мнимой частям элемента матрицы. Во всех этих случаях после создания области графика необходимо указать вместо заполнителя имя матрицы, содержащей необходимые значения.

Для построения параметрического точечного графика командой требуется задать три вектора с одинаковым числом элементов, которые соответствуют х-, у- и z-координатам точек, отображаемых на графике. В области графика эти три вектора указываются внутри скобок через запятую. Аналогичным образом можно построить поверхность, заданную параметрически. Для этого надо задать три матрицы, содержащие, соответственно, х-, у- и z-координаты точек поверхности. В шаблоне в области графика эти три матрицы указываются в скобках через запятую.

Таким образом, можно построить практически любую криволинейную поверхность, в том числе с самопересечениями.

Источник

Как построить график в «Маткаде»? Советы и рекомендации

Mathcad является универсальным инструментом у тех людей, которые плотно связали свою жизнь с вычислениями. «Маткад» способен производить сложные математические расчеты и мгновенно выдавать ответ на экране. Студенты или те, кто в первый раз столкнулся с этой программой, задают множество вопросов, на которые не могут дать ответ самостоятельно. Один из них, затрудняющий дальнейшее обучение: как построить график в «Маткаде»? На самом деле, это не так сложно, как может показаться. Постараемся разобраться также в том, как в «Маткаде» построить график функции, как строить несколько функций, узнаем о некоторых элементах отображение графика на экране.

Быстрый график в Mathcad

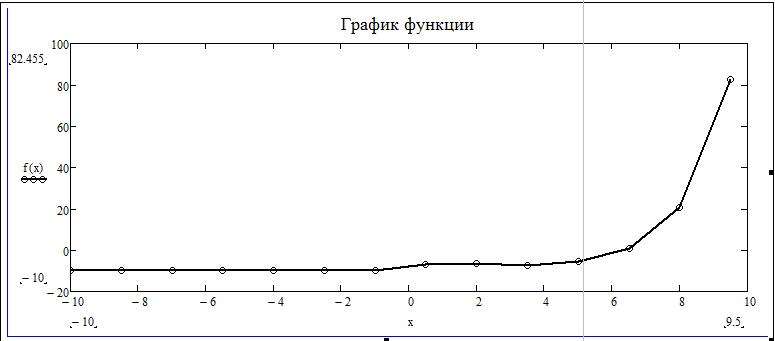
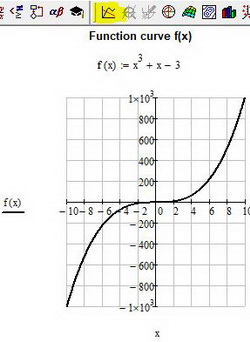
Возьмем одну функцию и будем проводить все ниже перечисленные операции с ней. Допустим, имеем следующее техническое задание: построить график функции f(x) = (e^x/(2x-1)^2)-10 на интервале [-10;10], исследовать поведение функции.

Итак, перед тем как построить график в «Маткаде», нужно переписать нашу функцию в математическую среду. После этого просто прикинем возможный график без масштабирования и всего прочего.

Построение дополнительных графиков

График, построенный по набору значений

Перед тем как построить график в «Маткаде» по точкам, необходимо создать диапазон значений. Сразу отметим, что график, построенный по точкам, иногда бывает неточным, так как может найтись такая точка, которая не попадет в диапазон значений, но в оригинальном графике в ней происходит разрыв. В этом примере специально будет показан этот случай.

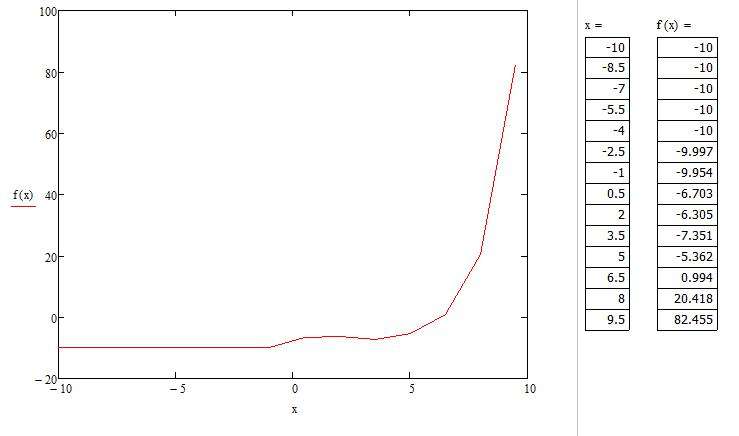
Нам необходимо задать диапазон значений. Для этого присвоим значения переменной (x:=-10,-8.5.. 10). Когда пользователь будет задавать диапазон, ему следует знать, что двоеточие ставится через символ «;». Теперь для визуального восприятия отобразим все значения «х» и «f(x)» в программе. Для этого необходимо ввести «х=» и, соответственно, «f(x)=». Теперь заново построим график функции, только в этот раз по точкам.

Мы видим, что на графике, построенном по точкам, не отображается та точка, которая осуществляет разрыв на исходном графике. То есть можно сделать вывод о том, что построение по точкам может не учитывать значения функции, которые создают разрыв.

Настройка отображения графика

Источник

Как построить диаграмму

Вложения

7 лаба.rar (49.3 Кб, 15 просмотров)

Как построить диаграмму Парето в Mathcad
Помогите пожалуйста! Нужно построить Диаграмму Парето в маткаде! В эксель знаю как, а вот с.

Подскажите, как построить диаграмму направленности
Здравствуйте,помогите построить ДН для щелевой антенны.

Построить косекансную диаграмму направленности
Касекансная диаграмма направленности Доброго времени суток! Помогите пожалуйста разобраться с.

Не могу построить график(фазовую диаграмму dx от х)
Здравствуйте не могу построить график в среде Mathcad, с программой только начал разбираться.

Решение

Интерполяция в MathCade, построить диаграмму растяжения
Помогите выполнить задание: Построить диаграмму деформирования по полученным данным с.

Построить диаграмму направленности петлевой рамочной антенны
Добрый день, помогите, пожалуйста, нужно построить диаграмму направленности петлевой рамочной.

Построить диаграмму направленности системы вибратор+рефлектор
Всем доброго времени суток. Помогите пожалуйста разобраться. Требуется рассчитать ДН системы.

Построить диаграмму направленности
Зосима, привет! можешь помочь с диаграммой направленности?)))очень очень очень нужно) Зосима.

Построить диаграмму направленности (ДН)
Преподаватель дал задание и сказал принести код, на следующей неделе.А мои познание в Matlab далеки.

Источник

Построение графиков в MathCad

В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:

Построение графика по точкам

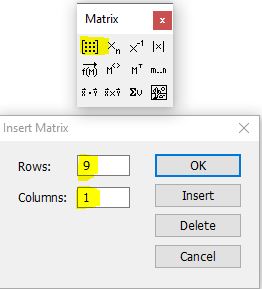
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)

Рис. 1. Создание матриц-столбцов

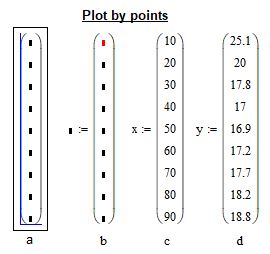
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.

Рис. 2. Заполнение матриц-столбцов для графика

На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)

Рис. 3. Создание заготовки для графика

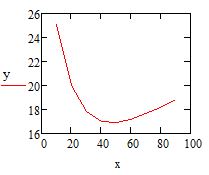
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)

Рис. 4. График по точкам

Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)

Рис. 5. Настройка отображения графика

Построение графика функции f(x)

Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой

Рис. 6. Построение графика функции f(x)

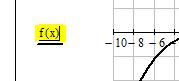
Рис. 7. Построение двух графиков функции

Построение эпюры в mathcad

Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:

— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
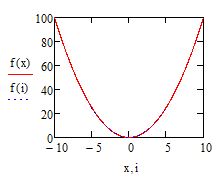
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании

Рис. 8. Ввод ранжированной переменной

Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже

Рис. 9. Ввод ранжированной переменной

Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже

Рис. 10. Построение эпюры. Шаг 1

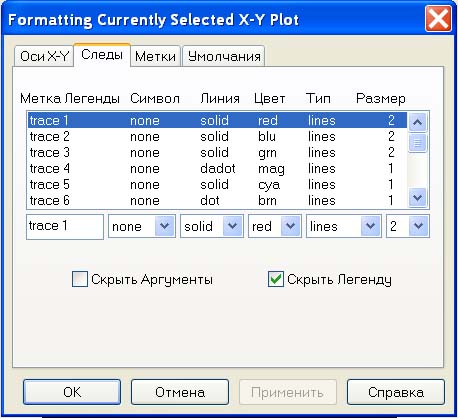
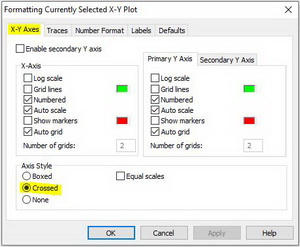
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.

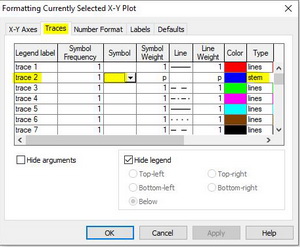
Рис. 11. Построение эпюры. Шаг 2

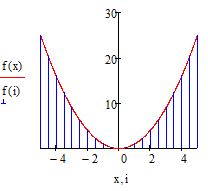
В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)

Рис. 12. Построение эпюры. Шаг 3

Построение графика в полярных координатах в mathcad

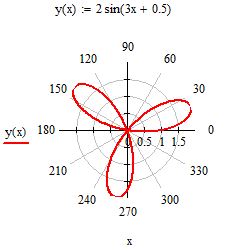
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)

Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph

Рис. 13. Создание загатовки для графика в полярных координатах

Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.

Рис. 14. Построение графика в полярной системе координат

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Источник

Урок 8. 2D-графики функций в Mathcad

В этом уроке мы рассмотрим варианты графиков, доступных в PTC Mathcad Prime 3.0.

Типы графиков

Чтобы изменить тип графика, нажмите на него, затем выберите на вкладке Графики –> Кривые –> Изменить тип. Ниже представлены рисунки четырех типов графиков для функции:

В списке есть еще некоторые типы осей – некоторые из них мы будем использовать позднее.

Несколько графиков на одних осях

Чтобы добавить кривую на оси, поместите курсор после обозначения легенды оси Y графика и нажмите Графики –> Кривые –> Добавить кривую. Появится еще один местозаполнитель для оси Y:

Вы можете добавить больше графиков с помощью этой же команды.

С помощью вывода нескольких графиков на одни оси мы посмотрим различные настройки из меню Графики –> Стили. Для этой цели мы создадим оси с пятью различными прямыми линиями. Каждая линия содержит 11 точек:

Ниже этих выражений вставьте график XY, затем добавьте четыре легенды для оси Y. В местозаполнителе для оси Xвведите x[iи нажмите [Enter] – для всех пяти графиков будет использоваться одна легенда по оси X. В последний местозаполнитель для оси Y введите y[0,i и [Enter]:

Выше следует ввести y[1,i, еще выше — y[2,i и т.д. После завершения Вы увидите пять прямых линий. Свойства каждой из них можно изменить, выбрав легенды оси Y соответствующего графика и выбрав необходимые настройки на меню Графики –> Стили.

Ниже представлены получившиеся графики. Использовались различные настройки для толщины, цвета, стиля линий и символов:

Метки и их значения мы убрали с помощью меню Графики –> Оси.

Масштабирование

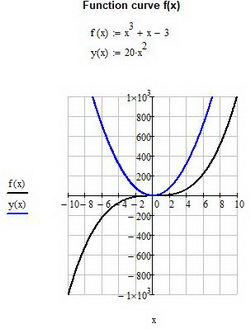
На графике с двумя кривыми диапазон для одной из них может быть не очень удачным для другой, например, для графиков квадрата и куба x.

Чтобы исправить это, разделите функцию куба на 5. Это называется масштабированием:

Маркеры

Чтобы узнать точные значения по графику, можно использовать маркеры из меню Графики –> Маркеры. Стиль линий маркеров можно изменять таким же способом, как и для обычных графиков:

Кривая «Столбцы»

Рассмотрим тип кривой «Столбцы». Для этого используем таблицу с данными – вкладка Матрицы/таблицы –> Вставить таблицу и в появившейся сетке выберите таблицу с 2 столбцами и 10 строками:

В местозаполнителях заголовка введите x и y. Числа заполните, как на рисунке:

Вставьте график XY. Улучшите вид графика, переместив легенды по осям и отформатировав значения меток. Чтобы поменять тип графика, выберите Графики –> Кривые –> Изменить тип –> Кривая «столбцы»:

Таблица данных в Mathcadцелесообразно использовать, если данных немного. Для большого числа данных лучше совместно использовать Mathcad и Excel – об этом мы поговорим в уроке 17.

Полярный график

Построим график спирали в полярных координатах:

Вставьте полярный график с помощью Графики –> Кривые –> Вставить график –> Полярный график. В местозаполнители введите данные, как на рисунке, и нажмите [Enter]:

Параметрический график

Этот график окружности построен с использованием параметра t:

Графики в логарифмическом масштабе

Логарифмический масштаб часто используется в различных областях науки и техники. Построение графиков в логарифмическом масштабе доступно в Mathcad.

Чтобы сделать ось X логарифмической, выберите легенду оси X и нажмите Графики –> Оси –> Логарифмический масштаб. Проделайте то же самое для оси Y. В логарифмическом масштабе эта функция представляет собой прямую линию:

Резюме

В этом уроке мы показали, как можно модифицировать двумерные графики.

Источник