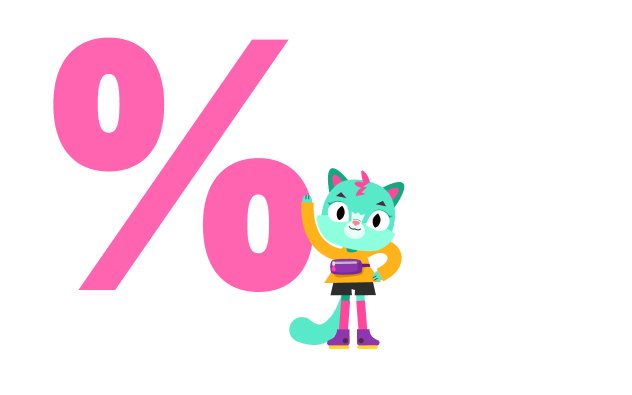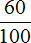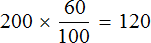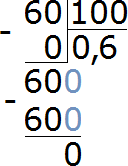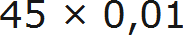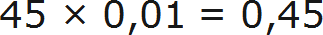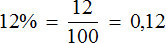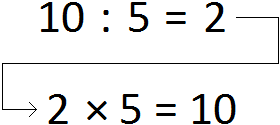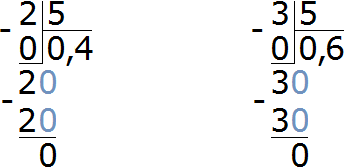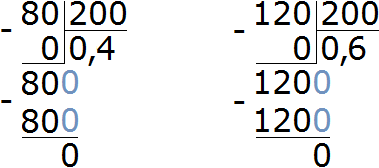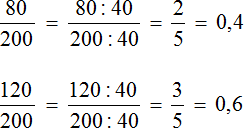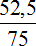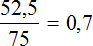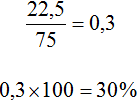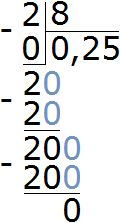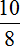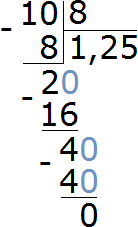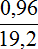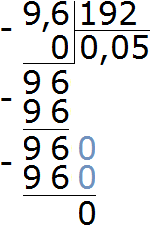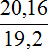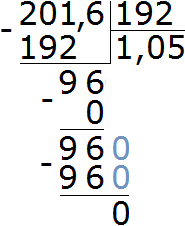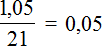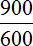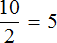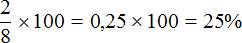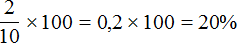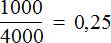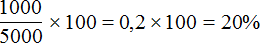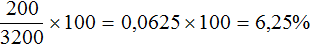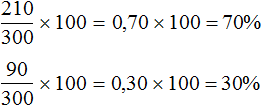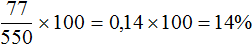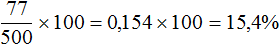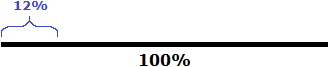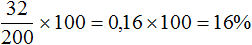Как посчитать задачу с процентами

Как решать задачи с процентами

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

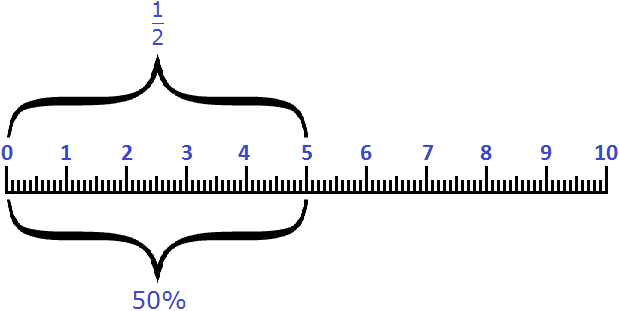
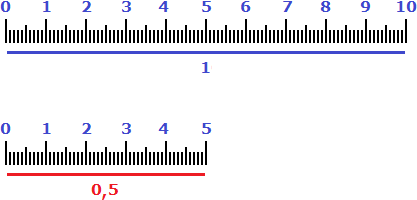
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

А вот, как перевести проценты в десятичную дробь — обратным действием:

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

Из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

38/0,16 = 38 * 100/16 = 237,5

Значит 237 задачи включили в этот сборник.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: возьмем алгоритм из правила выше:

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%

В классе учится 10 девочек — это 40%.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

Формула расчета процента от числа выглядит так:

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: подставим в формулу данные из условий задачи.

110 * (1 + 12/100) = 110 * 1,12 = 123,2.

Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

Формула расчета выглядит так:

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?

Как решаем: подставим в формулу данные из условий задачи.

75 выпускников закончат школу в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?

Как решаем: подставим в формулу данные из условий задачи.

5000 * (1 + 12 * 15/100) = 14000

Родители через год внесут в банк 14000 рублей.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.

Как решаем: просто подставим в формулу данные из условий задачи:

25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.

Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!

Способы нахождения процента

Универсальная формула для решения задач на проценты:

Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.

Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой.

С помощью метода пропорции можно рассчитать любые %. Выглядит это так:

Читается: a относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.

Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Ответ: купить спортивную футболку выгоднее на 194,6 рубля.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

76 : 100 = 0,76 — 1% от массы человека

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

После двух понижений изменение цены составит:

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Источник

Задачи на нахождение процента

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие процентов

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %.

А вот, как перевести проценты в десятичную дробь — обратным действием:

Примеры с процентами

Пример 1

Найдите 60% от числа 250.

Решение:

Число 250 будет нашим целым, то есть это 100%. Нам нужно найти 60%. Отношение 60 к 100 будет равно отношению неизвестного числа к 250:

Произведение крайних будет равно произведению внутренних, то есть 100 умножить на Х равно 250 умножить на 60:

Решаем простое уравнение и получаем 150.

Ответ: 150

Пример 2

Найдите число, если его 40% равняется 100.

Решение:

Решаем по алгоритму из первого примера, только здесь неизвестен один из крайних элементов.

Ответ: 250

Примеры задач на проценты с решением

Для полного понимания задач на проценты, необходимо решить реальные примеры из жизни. Этим и займемся🤓

Задача 1

Интернет-магазин закупился 1000 айфонами. Но вот беда: 3% процентов из них оказались бракованными. Сколько айфонов из 1000 бракованные?

Решение:

Всего у магазина 1000 айфонов — это 100%. Отношение 3% к 100 будет равно отношению бракованных айфонов к их общему количеству:

Ответ: 30 айфонов — бракованные.

Задача 2

Школа купила 250 парт: 225 из них — полностью годны для использования. Какой процент парт исправны, а сколько процентов оказались браком?

Решение:

250 парт — это 100 процентов. По простой пропорции отношения исправных парт к общему числу и их процентов к 100 находим долю.

225 х 100 = 250 х Х

90 процентов парт — готовы разбежаться по кабинетам, с ними все в порядке. Значит с остальными партами что-то не так: то ли ножки кривые, то ли краска слезла. Выходит: 100 – 90 = 10. 10 процентов парт бракованы.

Ответ: 90% годны и 10% бракованы.

Задача 3

Цена за килограмм арбуза увеличилась на 8 рублей — это на 10% больше прежней цены. Сколько раньше стоил килограмм арбуза?

Решение:

Если 8 рублей — это 10 процентов, то по пропорции находим 100%.

Ответ: до подорожания арбуз стоил 80 рублей за килограмм.

Задача 4

Число собачек-мальчиков в питомнике относится к числу всех собак, как 1/15. Общее число собак в питомнике — 120. Сколько всего собак-мальчиков и каков их процент?

Решение:

Сначала нужно найти число собак-мальчкиков. Нам дано отношение 1/15. По пропорции находим:

Число собак-мальчиков — 8. Всего их 120, то есть по еще одной пропорции находим их долю.

Ответ: 6.67 процентов собак — мальчики, а всего их 8.

Задача 5

25% фотографий в инстаграме одноклассника — это 150 штук. Сколько всего у него фоток в аккаунте?

Решение:

Если 25% — это 150, то нужно найти значение 100 процентов.

Ответ: у одноклассника 600 фотографий.

Задача 6

Артем купил 15 яблок — 3 из них оказались гнилыми. Он выбросил их и купил еще 8. Теперь гнилых яблок было 2, а яблок всего 20. Насколько процентов снизилась доля гнилых яблок?

Решение:

Сначала гнилых яблок было 3 из 15 — это 20% от общего количества.

Потом Артем купил еще 8 — теперь их стало 20. Но 2 яблока оказались гнилыми. То есть процент гнилых яблок теперь стал 10%.

Ответ: процент гнилых яблок снизился на 10%

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Источник

Задачи на проценты

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на проценты. Мы рассмотрим несколько задач, а также затронем те моменты, которые не упоминали ранее при изучении процентов, посчитав что на первых порах они создают трудности для обучения.

Большинство задач на проценты сводятся к тому, чтобы найти процент от числá, найти число по проценту, выразить в процентах какую-либо часть, либо выразить в процентном соотношении взаимосвязь между несколькими объектами, числами, величинами.

Способы нахождения процента

Процент можно находить различными способами. Самый популярный способ — разделить число на 100 и умножить полученный результат на искомое количество процентов.

Например, чтобы найти 60% от 200 рублей, нужно сначала эти 200 рублей разделить на сто равных частей:

200 руб : 100 = 2 руб.

Когда мы делим число на 100, мы тем самым находим один процент от этого числа. Так, разделив 200 рублей на 100 частей, мы автоматически нашли 1% от двухсот рублей, то есть узнали сколько рублей прихóдится на одну часть. Как видно из примера, на одну часть (на один процент) приходится 2 рубля.

1% от 200 рублей — 2 рубля

Зная сколько рублей приходится на одну часть (на 1%), можно узнать сколько рублей приходится на две части, на три, на четыре, на пять и т.д. То есть можно найти любое количество процентов. Для этого достаточно умножить эти 2 рубля на искомое количество частей (процентов). Давайте найдём шестьдесят частей (60%)

2 руб × 60 = 120 руб.

2 руб × 90 = 180 руб.

2 руб × 100 = 200 руб.

100% это все сто частей и они составляют все 200 рублей.

Второй способ заключается в том, чтобы представить проценты в виде обыкновенной дроби и найти эту дробь от того числа, откуда требуется найти процент.

Например, найдем те же 60% от 200 рублей. Сначала предстáвим 60% в виде обыкновенной дроби. 60% это шестьдесят частей из ста, то есть шестьдесят сотых:

Третий способ заключается в том, чтобы представить процент в виде десятичной дроби и умножить число на эту десятичную дробь.

Например, найдем те же 60% от 200 рублей. Для начала представляем 60% в виде дроби. 60% процентов это шестьдесят частей из ста

Выполним деление в этой дроби. Перенесем запятую в числе 60 на две цифры влево:

Теперь находим 0,60 от 200 рублей. Для нахождения десятичной дроби от числа, нужно это число умножить на десятичную дробь:

Приведенный способ нахождения процента является наиболее удобным, особенно если человек привык пользоваться калькулятором. Этот способ позволяет найти процент в одно действие.

Как правило выразить процент в десятичной дроби не составляет особого труда. Достаточно приписать «ноль целых» перед процентной долей, если процентная доля представляет собой двузначное число, или приписать «ноль целых» и еще один ноль, если процентная доля представляет собой однозначное число. Примеры:

60% = 0,60 — приписали ноль целых перед числом 60, поскольку число 60 является двузначным

6% = 0,06 — приписали ноль целых и еще один ноль перед числом 6, поскольку число 6 является однозначным.

При делении на 100 мы воспользовались методом передвижения запятой на две цифры влево. В ответе 0,60 ноль, стоящий после цифры 6, сохранился. Но если выполнить это деление уголком, ноль исчезает — получается ответ 0,6

Надо помнить, что десятичные дроби 0,60 и 0,6 равны одному и тому же значению:

В том же «уголке» можно продолжать деление бесконечно, каждый раз приписывая к остатку ноль, но это будет бессмысленным действием:

Выражать проценты в виде десятичной дроби можно не только делением на 100, но и умножением. Значок процента (%) сам по себе заменяет собой множитель 0,01. А если учитывать, что число процентов и значок процента записаны слитно, то между ними располагается «невидимый» знак умножения (×).

Так, запись 45% на самом деле выглядит следующим образом:

Заменим знак процента на множитель 0,01

Данное умножение на 0,01 выполнятся путем перемещения запятой на две цифры влево:

Задача 1. Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 70% — деньги, заработанные папой. Какую часть заработала мама?

Решение

Всего процентов 100. Если папа заработал 70% денег, то остальные 30% денег заработала мама.

Задача 2. Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 70% — деньги, заработанные папой, а 30% — деньги, заработанные мамой. Сколько денег заработал каждый?

Решение

Найдем 70 и 30 процентов от 75 тыс. рублей. Так мы определим сколько денег заработал каждый. Для удобства 70% и 30% запишем в виде десятичных дробей:

75 × 0,70 = 52,5 (тыс. руб. заработал папа)

75 × 0,30 = 22,5 (тыс. руб. заработала мама)

Проверка

Ответ: 52,5 тыс. руб. заработал папа, 22,5 руб. заработала мама.

Задача 3. При остывании хлеб теряет до 4% своей массы в результате испарения воды. Сколько килограммов испарится при остывании 12 тонн хлеба.

Решение

Переведем 12 тонн в килограммы. В одной тонне тысяча килограмм, а в 12 тоннах в 12 раз больше:

1000 × 12 = 12 000 кг

Теперь найдем 4% от 12000. Полученный результат и будет ответом к задаче:

12 000 × 0,04 = 480 кг

Ответ: при остывании 12 тонн хлеба испарится 480 килограмм.

Задача 4. Яблоки при сушке теряют 84% своей массы. Сколько получится сушенных яблок из 300 кг свежих?

Найдем 84% от 300 кг

300 : 100 × 84 = 252 кг

300 кг свежих яблок в результате сушки потеряют 252 кг своей массы. Чтобы ответить на вопрос сколько получится сушенных яблок, нужно из 300 вычесть 252

Ответ: из 300 кг свежих яблок получится 48 кг сушенных.

Задача 5. В семенах сои содержится 20% масла. Сколько масла содержится в 700 кг сои?

Решение

Найдем 20% от 700 кг

Ответ: в 700 кг сои содержится 140 кг масла

Задача 6. Гречневая крупа содержит 10% белков, 2,5% жиров и 60% углеводов. Сколько этих продуктов содержится в 14,4 ц гречневой крупы?

Решение

Переведем 14,4 центнера в килограммы. В одном центнере 100 килограмм, в 14,4 центнерах в 14,4 раз больше

Найдем 10%, 2,5% и 60% от 1440 кг

1440 × 0,10 = 144 (кг белков)

1440 × 0,025 = 36 (кг жиров)

1440 × 0,60 = 864 (кг углеводов)

Ответ: в 14,4 ц гречневой крупы содержится 144 кг белков, 36 кг жиров, 864 кг углеводов.

Задача 7. Для лесопитомника школьники собрали 60 кг семян дуба, акации, липы и клена. Желуди составляли 60%, семена клена 15%, семена липы 20% всех семян, а остальное составляли семена акации. Сколько килограммов семян акации было собрано школьниками?

Решение

Примем за 100% семена дуба, акации, липы и клена. Вычтем из этих 100% проценты, выражающие семена дуба, липы и клена. Так мы узнаем сколько процентов составляют семена акации:

100% − (60% + 15% + 20%) = 100% − 95% = 5%

Теперь находим семена акации:

Ответ: школьниками было собрано 3 кг семян акации.

Проверка:

Задача 8. Купил человек продукты. Молоко стоит 60 рублей, что составляет 48% от стоимости всех покупок. Определить общую сумму денег, потраченных на продукты.

Решение

Это задача на нахождение числа по его проценту, то есть по его известной части. Такую задачу можно решать двумя способами. Первый заключается в том, чтобы выразить известное число процентов в виде десятичной дроби и найти неизвестное число по этой дроби

Выразим 48% в виде десятичной дроби

Зная, что 0,48 составляет 60 рублей, мы можем определить сумму всех покупок. Для этого нужно найти неизвестное число по десятичной дроби:

60 : 0,48 = 125 рублей

Значит, общая сумма денег, затраченных на продукты составляет 125 рублей.

Второй способ заключается в том, чтобы сначала узнать сколько денег приходится на один процент, затем полученный результат умножить на 100

48% это 60 рублей. Если мы разделим 60 рублей на 48, то узнаем сколько рублей приходится на 1%

60 : 48% = 1,25 рублей

На 1% приходится 1,25 рублей. Всего процентов 100. Если мы умножим 1,25 рублей на 100, получим общую сумму денег, затраченных на продукты

1,25 × 100 = 125 рублей

Задача 9. Из свежих слив выходит 35% сушенных. Сколько надо взять свежих слив, чтобы получить 140 кг сушенных? Сколько получится сушенных слив из 600 кг свежих?

Решение

Выразим 35% в виде десятичной дроби и найдем неизвестное число по этой дроби:

Чтобы получить 140 кг сушенных слив, нужно взять 400 кг свежих.

Ответим на второй вопрос задачи — сколько получится сушенных слив из 600 кг свежих? Если из свежих слив выходит 35% сушенных, то достаточно найти эти 35% от 600 кг свежих слив

Ответ: чтобы получить 140 кг сушенных слив, нужно взять 400 кг свежих. Из 600 кг свежих слив получится 210 кг сушенных.

Задача 10. Усвоение жиров организмом человека составляет 95%. За месяц ученик употребил 1,2 кг жиров. Сколько жиров может быть усвоено его организмом?

Решение

Переведем 1,2 кг в граммы

Найдем 95% от 1200 г

Ответ: 1140 г жиров может быть усвоено организмом ученика.

Выражение чисел в процентах

Процент, как было сказано ранее, можно представить в виде десятичной дроби. Для этого достаточно разделить число этих процентов на 100. Например, представим 12% в виде десятичной дроби:

Замечание. Мы сейчас не находим процент от чего-то, а просто записываем его в виде десятичной дроби.

Но возможен и обратный процесс. Десятичная дробь может быть представлена в виде процента. Для этого нужно умножить эту дробь на 100 и поставить знак процента (%)

Представим десятичную дробь 0,12 в виде процентов

Это действие называют выражением числа в процентах или выражением чисел в сотых долях.

Умножение и деление являются обратными операциями. К примеру, если 2 × 5 = 10, то 10 : 5 = 2

Точно так же деление можно записать в обратном порядке. Если 10 : 5 = 2, то 2 × 5 = 10:

Тоже самое происходит, когда мы выражаем десятичную дробь в виде процентов. Так, 12% были выражены в виде десятичной дроби следующим образом: 12 : 100 = 0,12 но потом эти же 12% были «возвращены» с помощью умножения, записав выражение 0,12 × 100 = 12%.

Аналогично можно выразить в процентах любые другие числа, в том числе и целые. Например, выразим в процентах число 3. Умножим данное число на 100 и к полученному результату добавим знак процента:

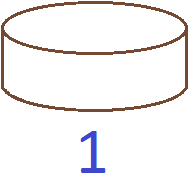
Большие проценты вида 300% поначалу могут сбивать с толку, поскольку человек привык считать 100% максимальной долей. Из дополнительных сведений о дробях мы знаем, что один целый объект можно обозначать через единицу. К примеру, если имеется целый не разрезанный торт, то его можно обозначить через 1

Этот же торт можно обозначить как 100% торта. В этом случае и единица и 100% будут обозначать один и тот же целый торт:

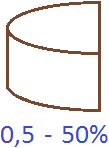
Разрежем торт пополам. В этом случае единица обратится в десятичное число 0,5 (поскольку это половина единицы), а 100% обратятся в 50% (поскольку 50 это половина от сотни)

Вернем обратно целый торт, единицу и 100%

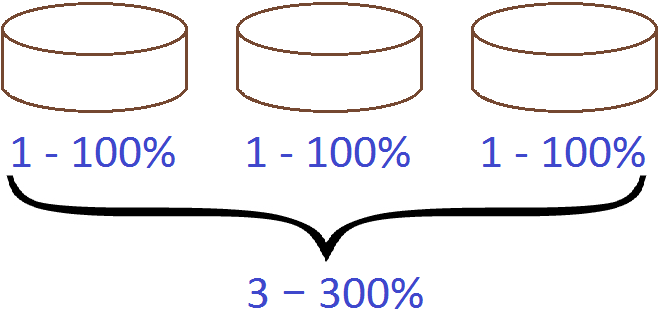
Изобразим ещё два таких торта с такими же обозначениями:

Если один торт является единицей, то три торта являются тремя единицами. Каждый торт является целым стопроцентным. Если сложить эти три сотни получится 300%.

Поэтому при переводе целых чисел в проценты, мы умножаем эти числа на 100.

Задача 2. Выразить в процентах число 5

Задача 3. Выразить в процентах число 7

Задача 4. Выразить в процентах число 7,5

Задача 5. Выразить в процентах число 0,5

Задача 6. Выразить в процентах число 0,9

Пример 7. Выразить в процентах число 1,5

Пример 8. Выразить в процентах число 2,8

Задача 9. Джордж идет со школы домой. Первые пятнадцать минут он прошел 0,75 пути. В остальное время он прошел оставшиеся 0,25 пути. Выразите в процентах части пути, пройденные Джорджом.

Решение

Задача 10. Джона угостили половиной яблока. Выразите эту половину в процентах.

Решение

Половина яблока записывается в виде дроби 0,5. Чтобы выразить эту дробь в процентах, умножим её на 100 и к полученному результату добавим знак процента

Аналоги в виде дробей

Величина, выраженная в процентах, имеет свой аналог в виде обычной дроби. Так, аналогом для 50% является дробь . Пятьдесят процентов также можно назвать словом «половина».

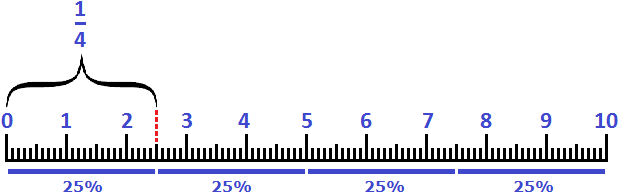
Аналогом для 25% является дробь . Двадцать пять процентов также можно назвать словом «четверть».

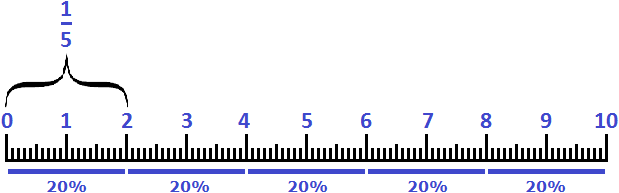
Аналогом для 20% является дробь . Двадцать процентов также можно назвать словами «пятая часть».

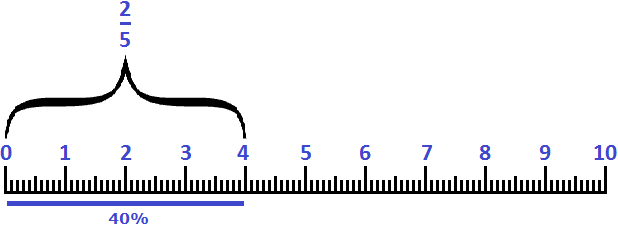
Аналогом для 40% является дробь .

Аналогом для 60% является дробь

Пример 1. Пять сантиметров это 50% от дециметра или или же просто половина. Во всех случаях речь идет об одной и той же величине — пяти сантиметрах из десяти

Пример 2. Два с половиной сантиметра это 25% от дециметра или или же просто четверть

Пример 3. Два сантиметра это 20% от дециметра или

Пример 4. Четыре сантиметра это 40% от дециметра или

Пример 5. Шесть сантиметров это 60% от дециметра или

Уменьшение и увеличение процентов

При увеличении или уменьшении величины, выраженной в процентах употребляется предлог «на».

Примеры:

Пример 1. Десять сантиметров увеличили на 50%. Сколько сантиметров получилось?

Чтобы решать подобные задачи, нужно исходную величину принимать за 100%. Исходная величина это 10 см. 50% от них составляют 5 см

Изначальные 10 см увеличили на 50% (на 5 см), значит получилось 10+5 см, то есть 15 см

Аналогом же увеличения десяти сантиметров на 50% является множитель 1,5. Если умножить на него 10 см получится 15 см

Поэтому выражения «увеличить на 50%» и «увеличить в 1,5 раза» говорят об одном и том же.

Пример 2. Пять сантиметров увеличили на 100%. Сколько сантиметров получилось?

Примем исходные пять сантиметров за 100%. Сто процентов от этих пяти сантиметров будут сами 5 см. Если увеличить 5 см на эти же 5 см, то получится 10 см

Аналогом же увеличения пяти сантиметров на 100% является множитель 2. Если умножить на него 5 см получится 10 см

Поэтому выражения «увеличить на 100%» и «увеличить в 2 раза» говорят об одном и том же.

Пример 3. Пять сантиметров увеличили на 200%. Сколько сантиметров получилось?

Примем исходные пять сантиметров за 100%. Двести процентов это два раза по сто процентов. То есть 200% от 5 см будут составлять 10 см (по 5 см на каждые 100%). Если увеличить 5 см на эти 10 см, то получится 15 см

Аналогом же увеличения пяти сантиметров на 200% является множитель 3. Если умножить на него 5 см получится 15 см

Поэтому выражения «увеличить на 200%» и «увеличить в 3 раза» говорят об одном и том же.

Пример 4. Десять сантиметров уменьшили на 50%. Сколько сантиметров осталось?

Примем исходные 10 см за 100%. Пятьдесят процентов от 10 см составляют 5 см. Если уменьшить 10 см на эти 5 см, останется 5 см

Аналогом же уменьшения десяти сантиметров на 50% является делитель 2. Если разделить на него 10 см, то получится 5 см

Поэтому выражения «уменьшить на 50%» и «уменьшить в 2 раза» говорят об одном и том же.

Пример 5. Десять сантиметров уменьшили на 80%. Сколько сантиметров осталось?

Примем исходные 10 см за 100%. Восемьдесят процентов от 10 см составляют 8 см. Если уменьшить 10 см на эти 8 см, останется 2 см

Аналогом же уменьшения десяти сантиметров на 80% является делитель 5. Если разделить на него 10 см, то получится 2 см

Поэтому выражения «уменьшить на 80%» и «уменьшить в 5 раз» говорят об одном и том же.

При решении задач на уменьшение и увеличение процентов, можно умножать/делить величину на указанный в задаче множитель.

Задача 1. Насколько процентов изменилась величина, если она увеличилась в 1,5 раза?

Величину о которой говорится в задаче можно обозначить как 100%. Далее умножить эти 100% на множитель 1,5

Теперь из полученных 150% вычтем изначальные 100% и получим ответ к задаче:

Задача 2. Насколько процентов изменилась величина, если она уменьшилась в 4 раза?

В этот раз будет происходить уменьшение величины, поэтому будем выполнять деление. Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 4

Из изначальных 100% вычтем полученные 25% и получим ответ к задаче:

Значит, при уменьшении величины в 4 раза она уменьшилась на 75%.

Задача 3. Насколько процентов изменилась величина, если она уменьшилась в 5 раз?

Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 5

Из изначальных 100% вычтем полученные 20% и получим ответ к задаче:

Значит, при уменьшении величины в 5 раз она уменьшилась на 80%.

Задача 4. Насколько процентов изменилась величина, если она уменьшилась в 10 раз?

Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 10

Из изначальных 100% вычтем полученные 10% и получим ответ к задаче:

Значит, при уменьшении величины в 10 раз она уменьшилась на 90%.

Задача на нахождение процентного соотношения

Чтобы выразить что-либо в процентном соотношении, сначала нужно записать дробь, показывающую какую часть первое число составляет от второго, затем выполнить деление в этой дроби и полученный результат выразить в процентах.

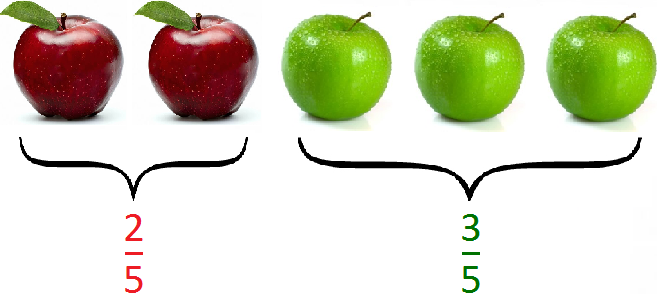
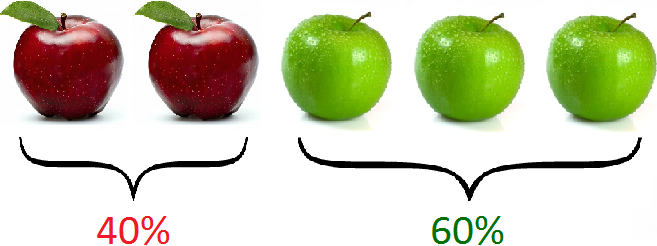
Например, пусть имеется пять яблок. При этом два яблока являются красными, три — зелеными. Выразим красные и зеленые яблоки в процентном соотношении.

Сначала нужно узнать какую часть составляют красные яблоки. Всего яблок пять, а красных два. Значит, два из пяти или две пятых составляют красные яблоки:

Зеленых же яблок три. Значит, три из пяти или три пятых составляют зеленые яблоки:

Имеем две дроби и . Выполним деление в этих дробях

Получили десятичные дроби 0,4 и 0,6. Теперь выразим в процентах эти десятичные дроби:

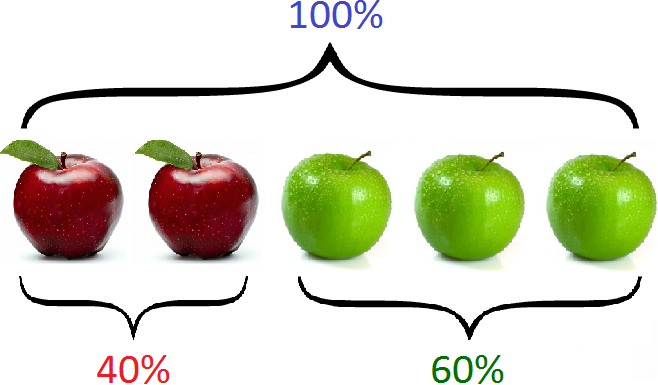
Значит, 40% составляют красные яблоки, 60% — зеленые.

А все пять яблок составляют 40%+60%, то есть 100%

Задача 2. Двум сыновьям мама дала 200 рублей. Младшему брату мама дала 80 рублей, а старшему 120 рублей. Выразите в процентном соотношении деньги, данные каждому брату.

Решение

Младший брат получил 80 рублей из 200 рублей. Записываем дробь восемьдесят двухсотых:

Старший брат получил 120 рублей из 200 рублей. Записываем дробь сто двадцать двухсотых:

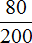
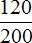
Имеем дроби и . Выполним деление в этих дробях

Выразим в процентах полученные результаты:

Значит, 40% денег получил младший брат, а 60% — старший.

Некоторые дроби, показывающие какую часть первое число составляет от второго, можно сокращать.

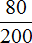
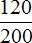
Так дроби и можно было бы сократить. От этого ответ к задаче не изменился бы:

Задача 3. Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 52,5 тыс. руб. — деньги, заработанные папой. 22,5 тыс. руб. — деньги, заработанные мамой. Выразите в процентах деньги, заработанные папой и мамой.

Решение

Данная задача, как и предыдущая, является задачей на нахождение процентного соотношения.

Выразим в процентах деньги, заработанные папой. Он заработал 52,5 тыс. рублей из 75 тыс. рублей

Выполним деление в этой дроби:

Выразим полученный результат в процентах:

Значит, папа заработал 70% денег. Далее нетрудно догадаться, что остальные 30% денег заработала мама. Ведь 75 тыс. рублей это все 100% денег. Для уверенности сделаем проверку. Мама заработала 22,5 тыс. руб. из 75 тыс. руб. Записываем дробь, выполняем деление и выражаем в процентах полученный результат:

Задача 4. Школьник тренируется делать подтягивания на перекладине. В прошлом месяце он мог делать 8 подтягиваний за подход. В этом месяце он может делать 10 подтягиваний за подход. На сколько процентов он увеличил количество подтягиваний?

Решение

Узнаем на сколько больше подтягиваний школьник делает в текущем месяце, чем в прошлом

Узнаем какую часть два подтягивания составляют от восьми подтягиваний. Для этого найдем отношение 2 к 8

Выполним деление в этой дроби

Выразим полученный результат в процентах:

Значит, школьник увеличил количество подтягиваний на 25%.

Эту задачу можно решить и вторым, более быстрым методом — узнать во сколько раз 10 подтягиваний больше, чем 8 подтягиваний и полученный результат выразить в процентах.

Чтобы узнать во сколько раз десять подтягиваний больше восьми подтягиваний, нужно найти отношение 10 к 8

Выполним деление в получившейся дроби

Выразим полученный результат в процентах:

Показатель подтягиваний в текущем месяце составляет 125%. Данное высказывание нужно понимать именно как «составляет 125%», а не как «показатель увеличился на 125%». Это два разных высказывания, выражающих различные количества.

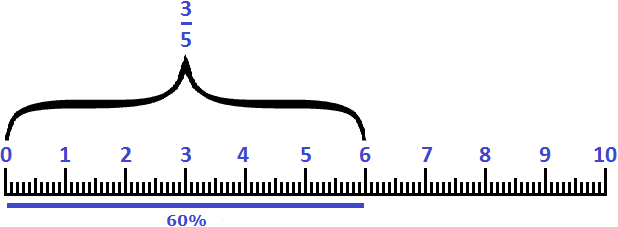
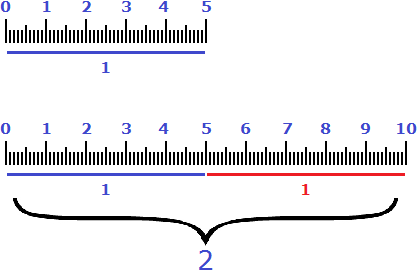
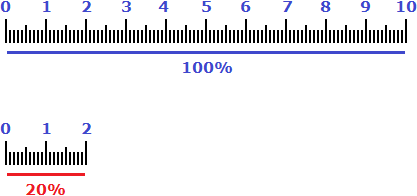
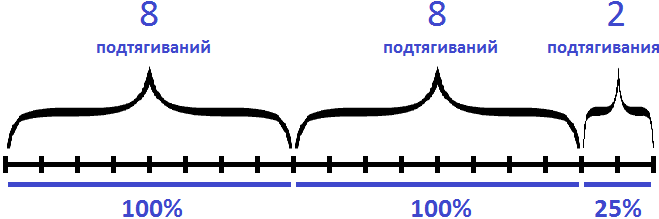
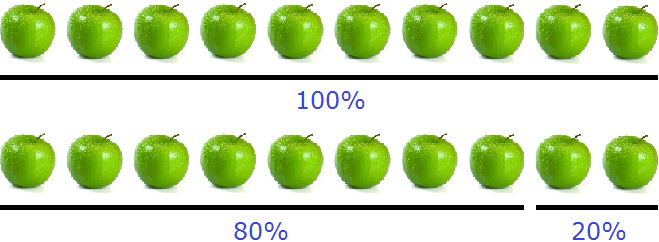
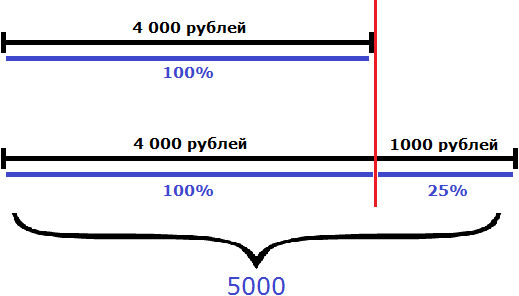
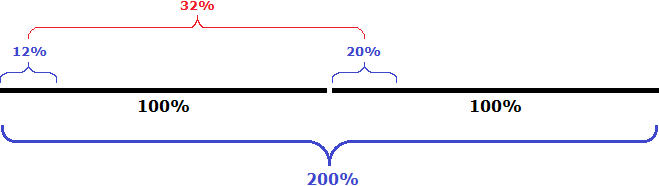
Высказывание «составляет 125%» нужно понимать как «восемь подтягиваний, которые составляют 100% плюс два подтягивания, которые составляют 25% от восьми подтягиваний». Графически это выглядит следующим образом:

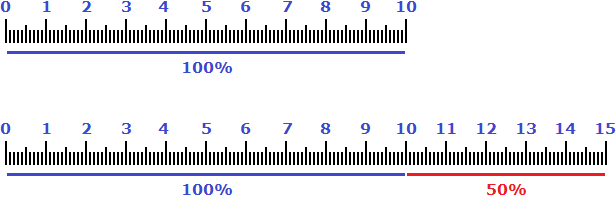
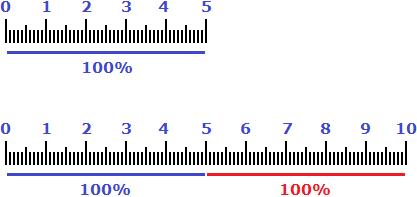
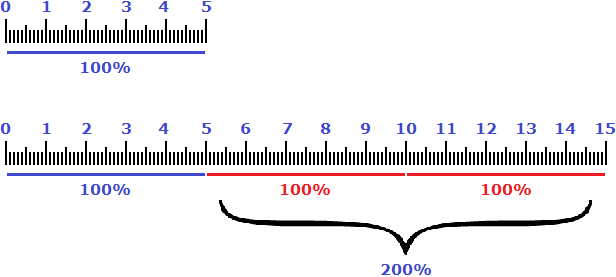
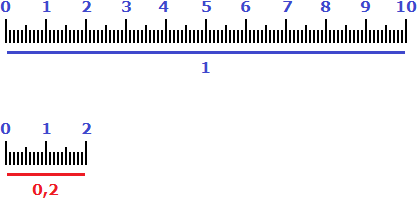
А высказывание «увеличился на 125%» нужно понимать как «к текущим восьми подтягиваниях, которые составляли 100% добавились еще 100% (еще 8 подтягиваний) плюс еще 25% (2 подтягивания)». Итого получается 18 подтягиваний

100% + 100% + 25% = 8 + 8 + 2 = 18 подтягиваний

Графически это высказывание выглядит следующим образом:

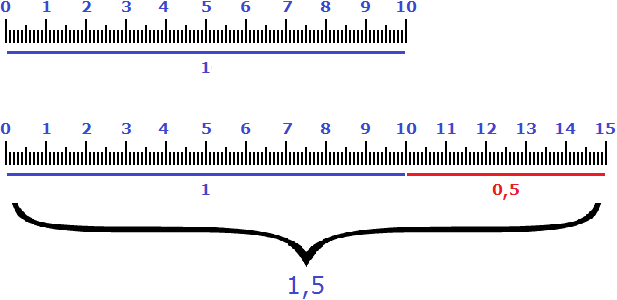
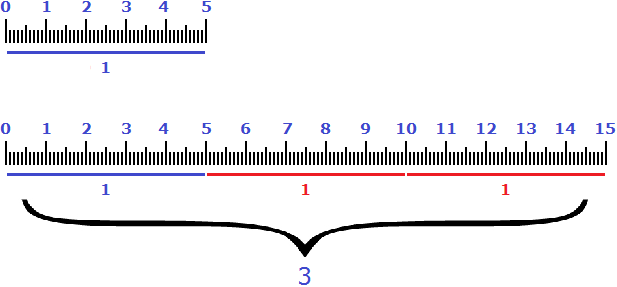
Всего же получается 225%. Если найти 225% от восьми подтягиваний, мы получим 18 подтягиваний

Задача 5. В прошлом месяце зарплата составляла 19,2 тыс. руб. В текущем месяце она составила 20,16 тыс. руб. На сколько процентов повысилась зарплата?

Эту задачу как и предыдущую можно решать двумя способами. Первый заключается в том, чтобы сначала узнать на сколько рублей увеличилась зарплата. Далее узнать какую часть эта прибавка составляет от зарплаты прошлого месяца

Узнаем на сколько рублей повысилась зарплата:

20,16 − 19,2 = 0,96 тыс. руб.

Узнаем какую часть 0,96 тыс. руб. составляет от 19,2. Для этого найдем отношение 0,96 к 19,2

Выполним деление в получившейся дроби. По пути вспомним, как выполняется деление десятичных дробей:

Выразим полученный результат в процентах:

Значит, зарплата повысилась на 5%.

Решим задачу вторым способом. Узнаем во сколько раз 20,16 тыс. руб. больше, чем 19,2 тыс. руб. Для этого найдем отношение 20,16 к 19,2

Выполним деление в получившейся дроби:

Выразим полученный результат в процентах:

Зарплата составляет 105%. То есть сюда входят 100%, которые составляли 19,2 тыс. руб., плюс 5% которые составляют 0,96 тыс. руб.

Задача 6. Цена ноутбука в этом месяце повысилась на 5%. Какова его цена, если в прошлом месяце он стоил 18,3 тыс. рублей?

Решение

Прибавим эти 5% к 18,3:

18,3 + 0,915 = 19,215 тыс. руб.

Ответ: цена ноутбука составляет 19,215 тыс. руб.

Задача 7. Цена ноутбука в этом месяце снизилась на 10%. Какова его цена, если в прошлом месяце он стоил 16,3 тыс. рублей?

Решение

Вычтем эти 10% из 16,3:

16,3 − 1,63 = 14, 67 (тыс. рублей)

Подобные задачи можно записывать кратко:

16,3 − (16,3 × 0,10) = 14,67 (тыс. рублей)

Ответ: цена ноутбука составляет 14,67 тыс. рублей.

Задача 8. В прошлом месяце цена ноутбука составляла 21 тыс. рублей. В этом месяце цена повысилась до 22,05 тыс. рублей. На сколько процентов повысилась цена?

Решение

Определим насколько рублей повысилась цена

22,05 − 21 = 1,05 (тыс. руб)

Узнаем какую часть 1,05 тыс. руб. составляет от 21 тыс. руб.

Выразим полученный результат в процентах

Ответ: цена ноутбука повысилась на 5%

Задача 8. Рабочий должен был изготовить по плану 600 деталей, а он изготовил 900 деталей. На сколько процентов он выполнил план?

Решение

Узнаем во сколько раз 900 деталей больше, чем 600 деталей. Для этого найдем отношение 900 к 600

Значение данной дроби равно 1,5. Выразим это значение в процентах:

Значит, рабочий выполнил план на 150%. То есть выполнил его на все 100%, изготовив 600 деталей. Затем изготовил еще 300 деталей, что составляет 50% от изначального плана.

Ответ: рабочий выполнил план на 150%.

Сравнение величин в процентах

Мы уже много раз сравнивали величины различными способами. Первым нашим инструментом была разность. Так, к примеру чтобы сравнить 5 рублей и 3 рубля, мы записывали разность 5−3. Получив ответ 2, можно было сказать, что «пять рублей больше трех рублей на два рубля».

Получаемый в результате вычитания ответ в повседневной жизни называют не «разностью», а «разницей».

Так, разница между пятью и тремя рубля составляет два рубля.

Следующим инструментом, которым мы воспользовались для сравнения величин, было отношение. Отношение позволяло нам узнать во сколько раз первое число больше второго (или сколько раз первое число содержит второе).

Так, к примеру десять яблок больше двух яблок в пять раз. Или по другому, десять яблок содержит два яблока пять раз. Данное сравнение можно записать с помощью отношения

Но величины можно сравнить и в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах.

Для сравнения величин в процентах, одну из них нужно обозначить как 100%, а вторую исходя из условий задачи.

Например, узнаем на сколько процентов десять яблок больше, чем восемь яблок.

За 100% нужно обозначить ту величину с которой мы что-либо сравниваем. Мы сравниваем 10 яблок с 8 яблоками. Значит, за 100% обозначаем 8 яблок:

Теперь наша задача сравнить на сколько процентов 10 яблок больше, чем эти 8 яблок. 10 яблок это 8+2 яблока. Значит, добавив к восьми яблокам ещё два яблока, мы увеличим 100% еще на какое-то число процентов. Чтобы узнать на какое именно, определим сколько процентов от восьми яблок составляют два яблока

Добавив эти 25% к восьми яблокам, мы получим 10 яблок. А 10 яблок это 8+2, то есть 100% и еще 25%. Итого получаем 125%

Значит, десять яблок больше восьми яблок на 25%.

Теперь решим обратную задачу. Узнаем насколько процентов восемь яблок меньше, чем десять яблок. Сразу напрашивается ответ, что восемь яблок меньше на 25%. Однако это не так.

Мы сравниваем восемь яблок с десятью яблоками. Мы договорились, что за 100% будем брать то, с чем сравниваем. Поэтому в этот раз за 100% берем 10 яблок:

Восемь яблок это 10−2, то есть уменьшив 10 яблок на 2 яблока, мы уменьшим их на какое-то число процентов. Чтобы узнать на какое именно, определим сколько процентов от десяти яблок составляют два яблока

Отняв эти 20% от десяти яблок, мы получим 8 яблок. А 8 яблок это 10−2, то есть 100% и минус 20%. Итого получаем 80%

Значит, восемь яблок меньше десяти яблок на 20%.

Задача 2. На сколько процентов 5000 рублей больше, чем 4000 рублей?

Решение

Примем 4000 рублей за 100%. 5 тысяч больше 4 тысяч на 1 тысячу. Значит, увеличив четыре тысячи на одну тысячу, мы увеличим четыре тысячи на какое-то количество процентов. Узнаем на какое именно. Для этого определим какую часть одна тысяча составляет от четырех тысяч:

Выразим полученный результат в процентах:

1000 рублей от 4000 рублей составляют 25%. Если прибавить эти 25% к 4000, то получится 5000 рублей. Значит, 5000 рублей на 25% больше, чем 4000 рублей

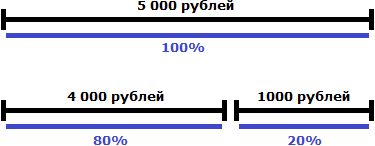
Задача 3. На сколько процентов 4000 рублей меньше, чем 5000 рублей?

В этот раз сравниваем 4000 с 5000. Примем 5000 за 100%. Пять тысяч больше четырех тысяч на одну тысячу рублей. Узнаем какую часть одна тысяча составляет от пяти тысяч

Тысяча от пяти тысяч составляет 20%. Если вычесть эти 20% от 5000 рублей, то получим 4000 рублей.

Значит, 4000 рублей меньше 5000 рублей на 20%

Задачи на концентрацию, сплавы и смеси

Допустим, возникло желание приготовить какой-нибудь сок. У нас в распоряжении имеется вода и малиновый сироп

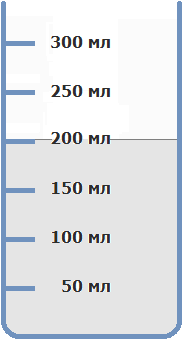
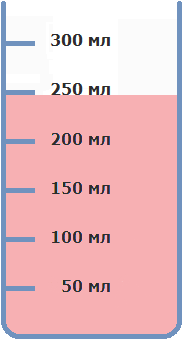
Нальем 200 мл воды в стакан:

Добавим 50 мл малинового сиропа и размешаем полученную жидкость. В результате у нас получится 250 мл малинового сока (200 мл воды + 50 мл сиропа = 250 мл сока)

Какую часть от получившегося сока составляет малиновый сироп?

Концентрацией растворённого вещества называют отношение количества растворённого вещества или его массы к объему раствора.

Концентрация обычно выражается в процентах. Давайте выразим концентрацию сиропа в процентах:

Таким образом, концентрация сиропа в малиновом соке составляет 20%.

Вещества в растворе могут быть неоднородными. Например, смешаем 3 л воды и 200 г соли.

Масса 1 л воды составляет 1 кг. Тогда масса 3 л воды будет составлять 3 кг. Переведем 3 кг в граммы, получим 3 кг = 3000 г.

Теперь в 3000 г воды опустим 200 г соли и смешаем полученную жидкость. В результате получится соленный раствор, общая масса которого будет составлять 3000+200, то есть 3200 г. Найдем концентрацию соли в полученном растворе. Для этого найдём отношение массы растворенной соли к массе раствора

Значит, при смешивании 3 л воды и 200 г соли получится 6,25%-й раствор соли.

При смешивании двух растворов получается новый раствор, состоящий из первого и второго растворов. У нового раствора концентрация вещества может быть другой. Полезным навыком является умение решать задачи на концентрацию, сплавы и смеси. В общем итоге смысл таких задач заключается в отслеживании изменений, которые происходят при смешивании растворов различной концентрации.

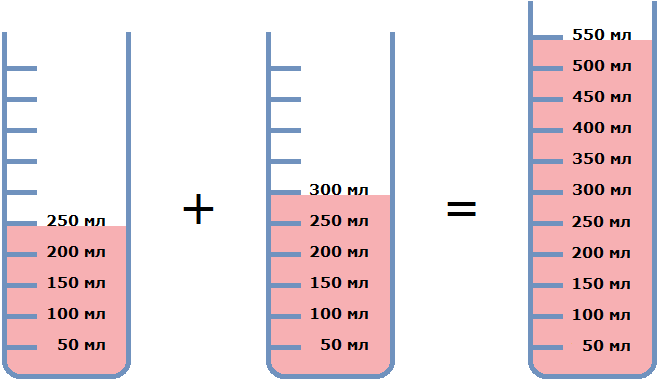
Смешаем два малиновых сока. Первый сок объемом 250 мл содержит 12,8% малинового сиропа. А второй сок объемом 300 мл содержит 15% малинового сиропа. Сольем эти два сока в большой стакан и смешаем. В результате получим новый сок объемом 550 мл.

Теперь определим концентрацию сиропа в полученном соке. Первый слитый сок объемом 250 мл содержал 12,8% сиропа. А 12,8% от 250 мл это 32 мл. Значит, первый сок содержал 32 мл сиропа.

Второй слитый сок объемом 300 мл содержал 15% сиропа. А 15% от 300 мл это 45 мл. Значит, второй сок содержал 45 мл сиропа.

Сложим количества сиропов:

32 мл + 45 мл = 77 мл

Эти 77 мл сиропа содержатся в новом соке, объем которого составляет 550 мл. Определим концентрацию сиропа в этом соке. Для этого найдём отношение 77 мл растворённого сиропа к объему сока 550 мл:

Значит, при смешивании 12,8%-го малинового сока объемом 250 мл и 15%‍-го малинового сока объемом 300 мл, получается 14%-й малиновый сок объемом 550 мл.

Задача 1. Имеются 3 раствора морской соли в воде: первый раствор содержит 10% соли, второй содержит 15% соли и третий — 20% соли. Смешали 130 мл первого раствора, 200 мл второго раствора и 170 мл третьего раствора. Определите сколько процентов составляет морская соль в полученном растворе.

Решение

Определим объем полученного раствора:

130 мл + 200 мл + 170 мл = 500 мл

Поскольку в первом растворе было 130 × 0,10 = 13 мл морской соли, во втором растворе 200 × 0,15 = 30 мл морской соли, а в третьем — 170 × 0,20 = 34 мл морской соли, то в полученном растворе будет содержаться 13 + 30 + 34 = 77 мл морской соли.

Определим концентрацию морской соли в полученном растворе. Для этого найдём отношение 77 мл морской соли к объему раствора 500 мл

Значит, в полученном растворе содержится 15,4% морской соли.

Задача 2. Сколько граммов воды надо добавить к 50 г раствора, содержащего 8% соли, чтобы получить 5%-й раствор?

Решение

Заметим, что если к имеющемуся раствору добавить воды, то количество соли в нём не изменится. Изменится только её процентное содержание, поскольку добавление воды в раствор приведёт к изменению его массы.

Нам нужно добавить такое количество воды при котором восемь процентов соли стали бы пятью процентами.

Определим сколько граммов соли содержится в 50 г раствора. Для этого найдем 8% от 50

8% от 50 г составляют 4 г. Другими словами, на восемь частей из ста приходятся 4 грамма соли. Давайте сделаем так, чтобы эти 4 грамма приходились не на восемь частей, а на пять частей, то есть на 5%

Теперь зная, что на 5% раствора приходятся 4 грамма, мы можем найти массу всего раствора. Для этого нужно найти число по его проценту:

4 г : 5 = 0,8 г
0,8 г × 100 = 80 г

80 граммов раствора это масса при которой 4 грамма соли будут приходиться на 5% раствора. А для получения этих 80 граммов, нужно к изначальным 50 граммам добавить 30 граммов воды.

Значит, для получения 5%-го раствора соли, нужно к имеющемуся раствору добавить 30 г воды.

Задача 2. Виноград содержит 91% влаги, а изюм – 7%. Сколько килограммов винограда требуется для получения 21 килограмма изюма?

Решение

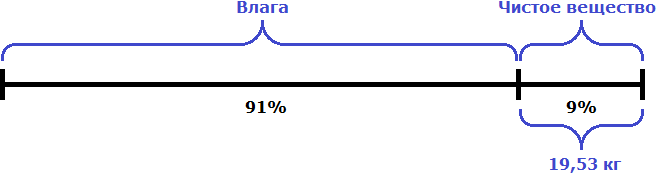
Виноград состоит из влаги и чистого вещества. Если в свежем винограде содержится 91% влаги, то на остальные 9% будет приходиться чистое вещество этого винограда:

Изюм же содержит 93% чистого вещества и 7% влаги:

Заметим, что в процессе превращения винограда в изюм, исчезает только влага этого винограда. Чистое вещество остаётся без изменения. После того, как виноград превратится в изюм, в получившемся изюме будет 7% влаги и 93% чистого вещества.

Определим сколько чистого вещества содержится в 21 кг изюма. Для этого найдем 93% от 21 кг

21 кг × 0,93 = 19,53 кг

Теперь вернемся к первому рисунку. Наша задача состояла в том, чтобы определить сколько винограда нужно взять для получения 21 кг изюма. Чистое вещество массой 19,53 кг будет приходиться на 9% винограда:

Теперь зная, что 9% чистого вещества составляют 19,53 кг, мы можем определить сколько винограда требуется для получения 21 кг изюма. Для этого нужно найти число по его проценту:

19,53 кг : 9 = 2,17 кг
2,17 кг × 100 = 217 кг

Значит, для получения 21 кг изюма нужно взять 217 кг винограда.

Задача 3. В сплаве олова и меди медь составляет 85%. Сколько надо взять сплава, чтобы в нём содержалось 4,5 кг олова?

Решение

Если в сплаве медь составляет 85%, то на остальные 15% будет приходиться олово:

Спрашивается сколько надо взять сплава, чтобы в нем содержалось 4,5 олова. Поскольку олова в сплаве содержится 15%, то 4,5 кг олова и будут приходиться на эти 15%.

А зная, что 4,5 кг сплава составляют 15% мы можем определить массу всего сплава. Для этого нужно найти число по его проценту:

4,5 кг : 15 = 0,3 кг
0,3 кг × 100 = 30 кг

Значит, сплава нужно взять 30 кг, чтобы в нём содержалось 4,5 кг олова.

Задача 4. Смешали некоторое количество 12%-го раствора соляной кислоты с таким же количеством 20%-го раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.

Решение

Изобразим на рисунке первый раствор в виде прямой линии и выделим на нём 12%

Поскольку количество растворов одинаково, рядом можно изобразить такой же рисунок, иллюстрирующий второй раствор с содержанием соляной кислоты 20%

Определим какую часть 32 части составляют от 200 частей

Значит, при смешивании 12%-го раствора соляной кислоты с таким же количеством 20%-го раствора этой же кислоты получится 16%-й раствор соляной кислоты.

Источник