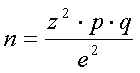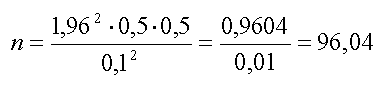Как посчитать выборку для исследования
Полезные статьи → Как правильно рассчитать объем выборки?
Один из главных компонентов тщательно продуманного исследования – определение выборки и что такое репрезентативная выборка. Это как в примере с тортом. Ведь не обязательно съедать весь десерт, чтобы понять его вкус? Достаточно небольшой части.

Высчитать генеральную совокупность сложно: нужно иметь данные переписи населения или предварительных оценочных опросов. Поэтому обычно генеральную совокупность «прикидывают», а из полученного числа высчитывают выборочную совокупность или выборку.
Что такое репрезентативная выборка?
Выборка – это чётко определенное количество респондентов. Её структура должна максимально совпадать со структурой генеральной совокупности по основным характеристикам отбора.

Объем выборки определяется с учётом требований точности и экономичности. Эти требования обратно пропорциональны друг другу: чем больше объем выборки, тем точнее результат. При этом чем выше точность, тем соответственно больше затрат необходимо на проведение исследования. И наоборот, чем меньше выборка, тем меньше на неё затрат, тем менее точно и более случайно воспроизводятся свойства генеральной совокупности.
Поэтому для вычисления объема выбора социологами была изобретена формула и создан специальный калькулятор:
Доверительная вероятность и доверительная погрешность
Что означают термины «доверительная вероятность» и «доверительная погрешность»? Доверительная вероятность – это показатель точности измерений. А доверительная погрешность – это возможная ошибка результатов исследования. К примеру, при генеральной совокупности более 500 00 человек (допустим, проживающие в Новокузнецке) выборка будет равняться 384 человека при доверительной вероятности 95% и погрешности 5% ИЛИ (при доверительном интервале 95±5%).
Что из этого следует? При проведении 100 исследований с такой выборкой (384 человека) в 95 процентов случаев получаемые ответы по законам статистики будут находиться в пределах ±5% от исходного. И мы получим репрезентативную выборку с минимальной вероятностью статистической ошибки.
После того, как подсчет объема выборки выполнен, можно посмотреть есть ли достаточное число респондентов в демо-версии Панели Анкетолога. А как провести панельный опрос можно подробнее узнать здесь.
socioline.ru
Расчет доверительного интервала
(«погрешность», ± % )
Если размер генеральной совокупности более 1 000 000 или сложно оценить точно иначе чем фразой «ну очень много» — можно просто оставить поле пустым.
Пояснения
Доверительная вероятность показывает, с какой вероятностью случайный ответ попадет в доверительный интервал. Для простоты можно понимать её как точность выборки. Как правило, используется 95%, но в условиях малых бюджетов и для небольших выборок, когда высокая точность не нужна, вероятностью можно пожертвовать и понизить её уровень до 90% и даже до 85% (главное не забыть учесть это в процессе анализа и в выводах). И наоборот, чем большую выборку может себе позволить исследователь, тем выше можно установить точность полученных данных.
Доверительный интервал можно понимать как погрешность, задает размах части кривой распределения по обе стороны от выбранной точки, куда могут попадать ответы.
Необходимы пояснения для тех, кто в первый раз сталкивается с понятиями доверительной вероятности и доверительного интервала. Например, выборка в 384 человека для генеральной совокупности более 500 000 человек (например, один из административных округов Москвы) означают доверительную вероятность 95% и доверительный интервал ±5%. То есть при проведении 100 исследований с такой выборкой (384 человека) в 95 процентов случаев получаемые ответы по законам статистики будут находиться в пределах ±5% от исходного.
Если еще упростить то, опросив 384 человка из полумиллиона и получив искомое значение «Х», можно утверждать, что 95% человек или 475 000 ответов попадут в интервал Х±5%, оставшиеся 25 000 ответов попадут «пальцем в небо», то есть за пределы полученного интервала.
Применяемые Формулы
Формулы расчета размера выборки, применяемые в калькуляторе.
Размер Выборки
где:
| Z = Z фактор (например 1,96 для 95% доверительного интервала) p = процент интересующих респондентов или ответов, в десятичной форме (0,5 по умолчанию) c = доверительный интервал, в десятичной форме (например, 0,04 = ±4%) |
Корректировка для малой генеральной совокупности
ss = размер выборки
css = скорректированная выборка
pop = генеральная совокупность
Приведенная ниже формула для расчета объема выборки используется в тех случаях, когда опрашиваемым (респондентам) задается только один вопрос, на который существует только два варианта ответа. Например: «Да» и «Нет», «Покупаю» и «Не покупаю», «Пользуюсь» и «Не пользуюсь». Конечно, данную формулу можно применять только при проведении простейших исследований. Если Вам нужно определить объем выборочной совокупности при проведении более масштабных исследований, например анкетирования, то следует использовать другие формулы.
Простая формула для расчета объема выборки
Ниже приведена простая формула для расчета объема выборки для тех случаев когда на заданный вопрос возможны лишь два варианта ответа:
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности (доверительного интервала, доверительной вероятности).
Этот показатель характеризует вероятность попадания ответов в специальный доверительный интервал — диапазон, границам которого соответствует определенный процент определенных ответов на некоторый вопрос.
Можно сказать, что уровень доверительности выражает вероятность того, что респонденты генеральной совокупности ответят так же, как и представители анализируемой выборки.
На практике доверительный интервал при проведении маркетинговых исследований часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58.
Также существует специальная таблица «Значение интеграла вероятностей», используя которую можно найти значение z для различных доверительных интервалов. Сокращенный вариант такой таблицы приведен ниже;
p – вариация для выборки, в долях.
Вариация характеризует величину схожести / несхожести ответов респондентов на вопрос. По сути, p — вероятность того, что респонденты выберут той или иной вариант ответа.
Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
e – допустимая ошибка, в долях.
Значение допустимой ошибки заранее определяют исследователь и заказчик маркетингового исследования.
Пример расчета объема выборочной совокупности
Маркетинговая компания получила заказ на проведение социологического исследования с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95% (одно из стандартных значений для маркетинговых исследований), тогда нормированное отклонение z = 1,96. Проведя предварительный анализ населения города, вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они — «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. исходя из требуемой заказчиком точности, допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Округлив расчетное значение, получаем объем выборки n = 96 человек.
Следовательно, для проведения исследования с заданными параметрами (уровень доверительности, допустимая ошибка) компании необходимо опросить 96 человек.
Значение нормированного отклонения для различных доверительных интервалов
В таблице приведены некоторые значения нормированного отклонения (z) для важнейших уровней доверительности, или, иначе, доверительной вероятности (α):
| α (%) | 60 | 70 | 80 | 85 | 90 | 95 | 97 | 99 | 99,7 |
|---|---|---|---|---|---|---|---|---|---|
| z | 0,84 | 1,03 | 1,29 | 1,44 | 1,65 | 1,96 | 2,18 | 2,58 | 3,0 |
Конечно, в таблице приведены значения z только для основных уровней доверительности. Полную версию таблицы можно найти в интернете.
Область применения простой формулы выборки
При проведении простых исследований, когда нужно получить ответ всего на один простой вопрос. При этом шкала ответов, как правило, дихотомического характера. То есть предлагаются (или подразумеваются) варианты ответов по типу «Да» — «Нет», «Черное» — «Белое», «Куплю» — «Не куплю», и т. д. Иными словами возможны лишь два варианта ответа на заданный вопрос.
Особенности формулы расчета размера выборки
Для рассмотренной нами простой формулы определения объема выборки можно выделить несколько характерных особенностей:
Также стоит отметить, что существует ряд иных формул для определения объема выборки в случаях с дихотомической шкалой ответов на единственный вопрос. Для более сложных маркетинговых исследований применяются другие формулы.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Как определить оптимальный размер выборки массового опроса
В каждой профессии есть свой набор любимых вопросов. Для исследователей рынка этот список возглавляет, безусловно, вопрос о размере выборки. Обычно его формулируют так:
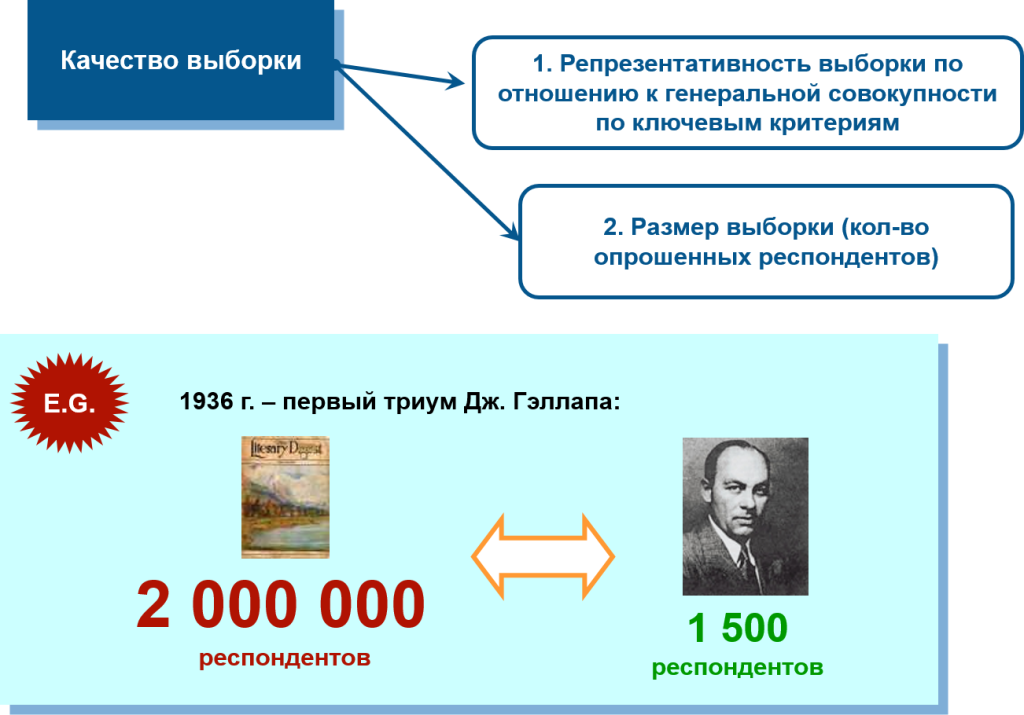
Главное заблуждение о размере выборки
Многие уверены, что чем больше размер целевой группы, тем больше должен быть размер выборки. Поэтому, якобы, чтобы узнать мнение жителей маленького города, достаточно опросить человек 200-300, ну а для выяснения мнения по России в целом и 5000 будет мало.
Между тем, этот стереотип не имеет ничего общего с реальностью. Размер выборки не зависит от численности целевой группы (на языке статистики она называется «генеральной совокупностью») и определяется двумя совершенно другими факторами. Единственное исключение из этого правила – случаи, когда генеральная совокупность очень маленькая, например, 1-2 тысячи человек, но такие ситуации в реальной практике маркетинговых исследований встречаются редко.
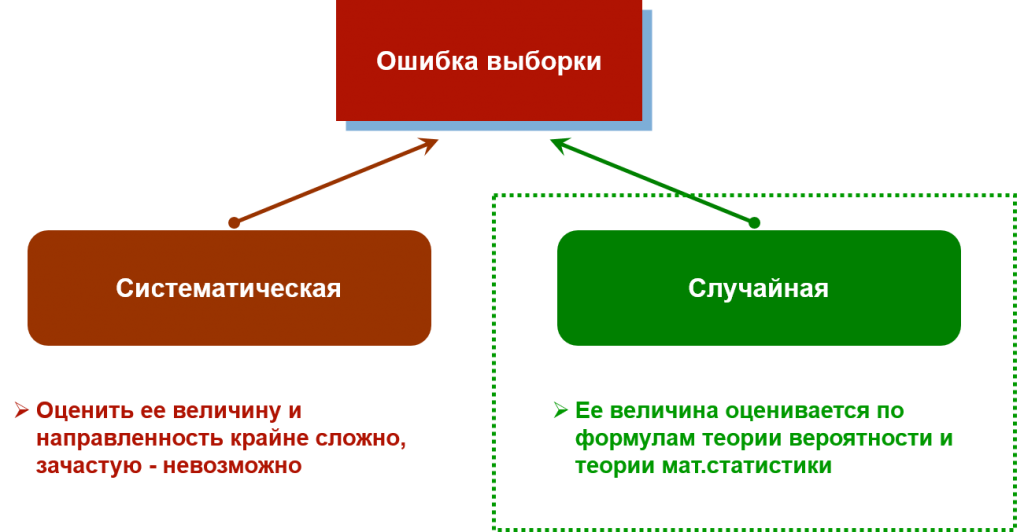
Две разновидности ошибки выборки
Любое выборочное наблюдение (то есть когда мы опрашиваем не всех подряд, а делаем случайный отбор из генеральной совокупности) сопряжено с погрешностью данных. Эту погрешность обычно называют «ошибкой выборки». Она может быть двух видов:
Задача исследователя – собрать данные так, чтобы минимизировать систематическую ошибку выборки. Тогда можно будет свести статпогрешность лишь к случайной ошибке, которую можно рассчитать по формулам.
Как рассчитать размер случайной ошибки выборки
Случайная ошибка выборки зависит не только от объема выборки, но и от дисперсии, то есть степени однородности данных. Чем однороднее данные (т.е. чем меньше разброс полученных значений, или дисперсия), тем меньше ошибка выборки.
Существует формула расчета случайной ошибки выборки, однако для удобства рекомендуем пользоваться онлайн-калькуляторами, например, вот этим. Он позволяет легко провести два вида расчета:
В качестве параметра доверительной надежности (одно из полей в калькуляторе) обычно используется значение в 95%. Это означает, что в 95% случаев распределение признака в генеральной совокупности попадет в рассчитанный доверительный интервал (т.е. само значение признака в выборке плюс-минус размер статистической погрешности). Реже используется значение надежности в 97% или 99% – оно, соответственно, означает, что подобное попадание произойдет в 97% или 99% случаев. В данном случае надежность выборки повышается, но увеличивается размер выборки.
Самое сложное при определении размера выборки – поиск компромисса между требуемой точностью и стоимостью сбора данных. Этот процесс усложняется тем, что увеличение размера выборки в четыре раза приводит к увеличению точности лишь в два раза (соответствует квадратному корню от величины прироста выборки).
Кейс: определение размера выборки для оценки потенциала рынка продаж столичной недвижимости покупателям из регионов
В ноябре-декабре 2016 года мы провели исследование спроса на квартиры в новостройках Москвы и Санкт-Петербурга со стороны жителей разных городов России. Исследование включало в себя три метода сбора данных: массовый репрезентативный опрос населения в возрасте от 20 до 60 лет (проводился с использованием технологии CATI), а также серию экспертных интервью с риэлторами и глубинных интервью с потенциальными покупателями квартир.
Исследование охватывало 33 города, отличающихся повышенным спросом на петербургскую и московскую недвижимость. Плановая выборка исследования, рассчитанная по формулам, составила 21 500 респондентов. Этот объем значительно больше «стандартного» объема выборки, используемого в маркетинговых исследованиях. С чем же связан такой большой размер выборки?
Все дело в том, что клиенту были нужны оценки отдельно по каждому городу, а не просто «в целом по стране». Фактически мы работаем не с 1 выборкой, а с 33 отдельными выборками по каждому городу. Доля людей, заинтересованных в покупке квартиры в Санкт-Петербурге или Москве, была экспертно определена в рамках 5% от числа жителей опрашиваемых городов.
В зависимости от важности города для заказчика, руководитель проекта со стороны Агентства определил допустимую статистическую погрешность, в которую должны укладываться итоговые результаты. Для этого мы использовали специальный макрос в MS Excel, но эти расчеты можно также выполнить с помощью калькулятора выборки. В результате размер выборки варьировал от 500 до 1000 респондентов по каждому из городов исследования, что в сумме и дало заявленные 21 500 человек.
Резюме
Чтобы рассчитать выборку маркетингового исследования, используйте следующий алгоритм:
Расчет размера выборки
Размер выборки требуется определить перед началом большинства количественных исследований. Определение размера выборки не требуется для качественных исследований
Когда необходимо рассчитывать размер выборки?
Почему размер выборки важен для маркетингового исследователя?
При проведении исследований, которые определяют распространенность некоей характеристики в популяции (мнении у целевой группы о том или ином предмете маркетинга или уровня охвата аудитории мероприятиями продвижения), расчет размера выборки необходим для того, чтобы полученные оценки имели желаемую степень точности.
Расчет размера выборки
Расчет доверительного интервала
(«погрешность», ± % )
Если размер генеральной совокупности более 1 000 000 или сложно оценить точно иначе чем фразой «ну очень много» — можно просто оставить поле пустым.
Пояснения
Доверительная вероятность показывает, с какой вероятностью случайный ответ попадет в доверительный интервал. Для простоты можно понимать её как точность выборки. Как правило, используется 95%, но в условиях малых бюджетов и для небольших выборок, когда высокая точность не нужна, вероятностью можно пожертвовать и понизить её уровень до 90% и даже до 85% (главное не забыть учесть это в процессе анализа и в выводах). И наоборот, чем большую выборку может себе позволить исследователь, тем выше можно установить точность полученных данных.
Доверительный интервал можно понимать как погрешность – размах части кривой распределения по обе стороны от выбранной точки, область, куда могут попадать все возможные ответы.
Необходимы пояснения для тех, кто в первый раз сталкивается с понятиями доверительной вероятности и доверительного интервала. Например, выборка в 384 человека для генеральной совокупности более 500 000 человек (например, один из административных округов Москвы) означают доверительную вероятность 95% и доверительный интервал ±5%. То есть при проведении 100 исследований с такой выборкой (384 человека) в 95 процентов случаев получаемые ответы по законам статистики будут находиться в пределах ±5% от исходного.
Если еще упростить то, опросив 384 человка из полумиллиона и получив искомое значение «Х», можно утверждать, что 95% человек или 475 000 ответов попадут в интервал Х±5%, оставшиеся 25 000 ответов попадут «пальцем в небо», то есть за пределы полученного интервала.
Применяемые Формулы
Формулы расчета размера выборки, применяемые в калькуляторе.
Размер Выборки
| Z = Z фактор (например 1,96 для 95% доверительного интервала) p = процент интересующих респондентов или ответов, в десятичной форме (0,5 по умолчанию) c = доверительный интервал, в десятичной форме (например, 0,04 = ±4%) |
Корректировка для малой генеральной совокупности
ss = размер выборки
css = скорректированная выборка
pop = генеральная совокупность