Как посчитать волновое сопротивление антенны
Калькулятор волнового сопротивления микрополосковой линии (формула Уилера)
Данный калькулятор поможет вам рассчитать волновое сопротивление (импеданс) микрополосковой линии.
Расчет
Входные данные:
Результаты:
Обзор
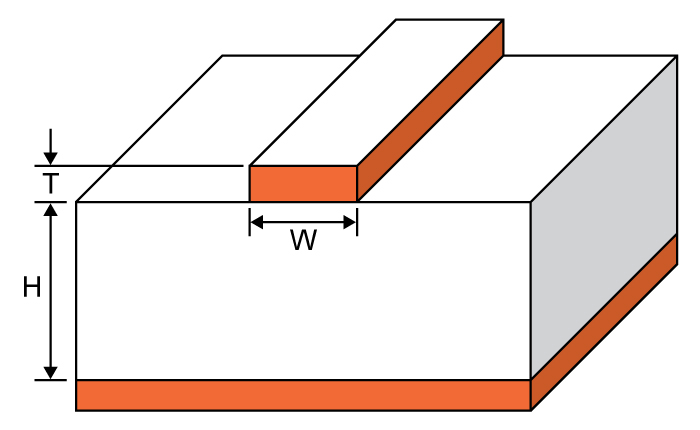
Данный калькулятор предназначен для расчета волнового сопротивления (импеданса) микрополосковой линии – плоского проводника, находящегося над полигоном земли с диэлектриком между ними (смотрите рисунок ниже). Хотя эта конструкция обычно изготавливается на базе печатных плат, она также может быть построена с использованием других материалов, если имеется проводник, отделенный от полигона земли некоторым диэлектрическим материалом.
Просто введите указанные значения толщины и ширины проводника (дорожки), высоты диэлектрической подложки и относительную диэлектрическую постоянную материала диэлектрика и нажмите кнопку «Расчет».
Формулы
Данная формула является асимптотической к точным результатам в трех разных случаях:
Утверждается, что для большинства других случаев погрешность расчета импеданса составляет менее 1% и всегда менее 2%.
Применение
С помощью микрополосковых линий могут создаваться СВЧ антенны и ответвители, а также некоторые фильтры. Поскольку микрополосковые линии представляют собой просто фигуры металлизации на подложке, они намного дешевле традиционных волноводов, а также более компактны и легче. Тем не менее, микрополосковые линии не могут обрабатывать такие высокие уровни мощности, как волноводы. Микрополосковые линии также имеют проблемы с потерями мощности, перекрестными помехами и непреднамеренным излучением, поскольку они не заключены в экран, как волновод.
Помимо применения в СВЧ, микрополосковые линии также можно найти в конструкциях высокоскоростных цифровых печатных плат. Такое применение влечет за собой перемещение сигнала с минимальными искажениями и отсутствием перекрестных помех и/или излучения – области, где микрополосковые лини отличаются превосходством, пока не обрабатываются очень высокие частоты.
Утилиты в (статусе FREE) для расчета волнового сопротивления и не только…
Каждый, кто связан с проектированием устройств в печатном исполнении, сталкивается с задачей определения волнового сопротивления проводников. И конечно же для многих конфигураций проводников можно найти готовые формулы (пусть и приближенные, но все-таки) и набить их, например, в Mathcad или же воспользоваться симуляторами, способными с заданной точностью рассчитать волновое сопротивление проводников. Все это есть, но в большинстве случаев не всегда удобно. Гораздо удобнее воспользоваться уже подготовленными утилитами (калькуляторами), которые помимо вычисления волнового сопротивления могут обладать набором вспомогательных полезных функций. О некоторых таких программах я и хотел бы сегодня рассказать.
Утилита от AWR “TXLine”.
Почти ничего лишнего, только расчет волнового сопротивления для проводников с различной конфигурацией. Есть следующие варианты:
• микрополосковая (несимметричная полосковая) линия – microstrip;
• симметричная полосковая линия – stripline;
• копланарная линия – CPW;
• копланарная линия с земляным слоем – CPWG;
• круглый коаксиал – round coaxial (конечно, выбивается из концепции печатной платы, но вдруг пригодится);
• щелевая линия – slotline;
• связанные микрополосковые линии – coupled microstrip lines;
• связанные симметричные полосковые линии – coupled stripline
Так же есть небольшое количество полезной информации: электрическая длина линии (пересчитывается в физическую длину); набег фазы на единицу длины линии; расчет эффективной относительной диэлектрической проницаемости; погонные потери в линии. Есть небольшой встроенный справочник по некоторым проводникам и диэлектрикам.
Не смотря на то, что утилита проста в использовании, можно найти обучающее видео на YouTube
Присутствуют наиболее распространенные типы линий. Казалось бы, что на этом можно и закончить, но мы продолжим.
Утилита “CITS25” от Polar. Содержит большое количество различных конфигураций печатных проводников и способна удовлетворить более взыскательного разработчика. Не буду описывать все возможности утилиты, скажу только, что есть конфигурации, например, с лицевой связью проводников (при этом можно задать смещение проводников относительно друг друга).
А так же есть симметричная копланарная линия со смещением относительно земляных слоев (шин, проводников).
Еще одна софтинка “AppCAD” от Agilent
Помимо уже перечисленных выше конфигураций проводников содержит так же:
• параллельные проволочные/проводные линии;
• провод над земляной плоскостью;
• и даже такую экзотическую конфигурацию, как “trough line” (не знаю, как корректно перевести этот термин на русский язык).
Однако помимо расчета волнового сопротивления для различных конфигураций проводников в AppCAD есть и другие ”вкусности”.
Есть возможность рассчитать трансформатор волновых сопротивлений на сосредоточенных элементах.
Есть возможность просматривать до трех файлов S-параметров одновременно. Можно подгружать как файлы двухполюсников *.s1p (например, антенна), так и файлы четырехполюсников *.s2p (фильтр, усилитель, сплиттер и т.д.). Можно посмотреть так же шумовые характеристики элемента.
Есть встроенный системный калькулятор.
А еще есть небольшой справочник c различными константами.
И даже этим набором функционал AppCAD не ограничивается. Есть еще много чего интересного и полезного.
А закончить я бы хотел софтинкой “RFSim99”, которую язык не повернется назвать калькулятором. Это маленькая САПР СВЧ. При этом она (софтинка) бесплатна и существует в русифицированном варианте.
В составе RFSim есть множество встроенных инструментов, способных облегчить жизнь разработчику:
• синтез цепи согласования, аттенюатора или фильтра;
• расчет параметров длинной линии, ответвителя или делителя мощности;
• так же есть простенький калькулятор/конвертер для расчета ряда параметров/величин.
А так же RFSim99 способна рассчитывать схемы, которые задает пользователь. Но это уже совсем другая история…
Про антенны для самых маленьких
Попробуем разобраться, как работают антенны и почему электромагнитная энергия из комфортного проводника излучается в чужеродный диэлектрик, причем обойдемся без матана, что потребует, разумеется, очень серьезных упрощений и даже вульгаризации, но все же позволит получить начальное представление и, не исключаю, желание почитать материалы для более продвинутых.
Если вы радиоинженер, опытный радиолюбитель-связист или просто хорошо знаете физику, то вам нижеследующее читать строго не рекомендуется во избежание негативных последствий для вашего психического здоровья. Вас предупреждали.
Начнем со скучных основ. В старые добрые времена, когда не было ни интернетов, ни этого вашего фидо, известные явления электричества и магнетизма не считались чем-то единым, имеющим общую природу, пока ровно двести лет назад датчанин Эрстед не обнаружил, что протекание электрического тока по проводнику вызывает отклонение стрелки компаса, т.е. создает доступное наблюдению и измерению простейшими приборами магнитное поле.
Вскорости француз Ампер вывел закон имени себя, описывающий зависимость электрического тока и возникающего от него магнитного поля, а чуть позже включившийся англичанин Фарадей обнаружил и математически изложил явление электромагнитной индукции. Спустя еще совсем немного времени шотландец Максвелл создает теорию электромагнитного поля, на которую нам бы и следовало опираться в дальнейшем рассказе, но мы договорились обходиться без матана настолько, насколько возможно, чтобы даже самые отпетые гуманитарии смогли почувствовать вкус к технике вместо быть распуганными сложными формулами. Все эти работы привели к тому, что 1887 году немец Герц экспериментально доказал существование радиоволн, построив радиопередатчик и радиоприемник, которые, довольно неожиданно, оказались рабочими. Впрочем, сам Герц перспектив своей радиопередачи (первой в мире!) не оценил и поэтому изобретение радио чаще связывают с итальянцем Маркони, который помимо неоспоримого инженерного гения, оказался успешен и в части коммерциализации. Да, если кому интересно, первая радиопередача голоса принадлежит канадцу Фесендену, которому удалось провернуть это дело в 1900 году.
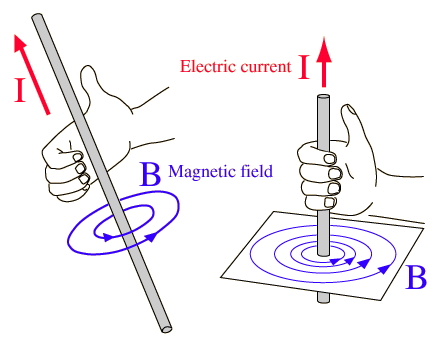
Ток в проводнике создает магнитное поле. Зачем же нам браться рукой за оголенный провод? Затем, чтобы легко запомнить направление вектора магнитного поля в зависимости от направления тока в проводнике — «правило правой руки».
Итак, теперь мы знаем, что протекание электрического тока в проводнике приводит к тому, что около проводника возникает магнитное поле. Вот это вот, если очень-очень упрощенно, и есть электромагнетизм. Поэтому первое, что мы можем усвоить: излучение антенн связано с протеканием в них электрического тока.
Радиосвязь использует переменный ток различной частоты (или длины волны – говоря об антеннах чаще удобнее говорить о длине волны, а о радиотехнике в целом – о частоте).
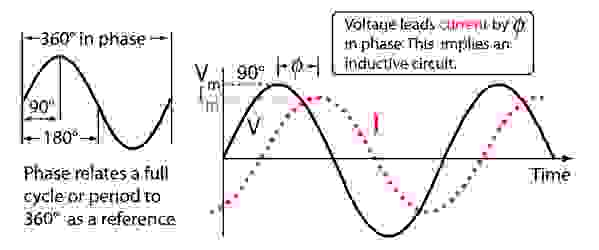
Различные частоты позволяют одновременно проводить много независимых передач и разделять их прием, выбирая нужные частоты и отбрасывая ненужные. Способов, как это сделать, довольно много, но они — тема отдельных статей. Переменный ток обладает одной неприятной особенностью: хотя он полностью подчиняется закону Ома (взаимозависимость напряжения, сопротивления цепи и тока в ней), напряжение и ток могут не совпадать по времени. Да-да, «сдвиг по фазе» – это необязательно в голове, это более чем электро- и радиотехнический термин. Вот что получается. Если бы мы подавали переменное напряжение на некий идеальный резистор, то синфазный переменный ток в этой цепи был бы равен напряжению в вольтах, деленному на сопротивление в омах – так же, как и приличный постоянный ток. Но если вместо резистора у нас катушка индуктивности, то дело становится более запутанным. Когда мы прикладываем напряжение к катушке, она как бы сопротивляется току через нее, поэтому ток отстает по фазе от напряжения. Кстати, если отключить подачу напряжения от катушки, то она тоже будет сопротивляться и постарается поддержать течение тока через себя (в той мере, в которой катушка может запасти энергию) – напряжения уже нет, а ток все еще идет. Вот это вот сопротивление, оно называется реактивным, тем выше, чем выше частота. То есть с ростом частоты при равной индуктивности или с ростом индуктивности при равной частоте сопротивление переменному току растет. С конденсаторами все то же самое, но только наоборот. При приложении напряжения к конденсатору ток сначала проваливается в него, как в пустую яму, опережая напряжение, а затем падает по мере заряда. Легкость, с которой переменный ток попадает в конденсатор, означает, что с ростом частоты при равной емкости сопротивление переменному току падает, а при равной частоте при росте емкости сопротивление переменному току также падает. Поэтому примем на заметку: реактивное сопротивление, то есть индуктивное или емкостное сопротивление переменному току, зависит от частоты.
Слева традиционная синусоидальная осциллограмма, справа сдвиг фаз на примере «отставания» тока от напряжения при наличии в цепи индуктивного сопротивления.
Суммарное сопротивление, состоящее из активной компоненты (условный резистор, который потребляет мощность «чисто», без влияния на фазу) и реактивной компоненты (сдвигающие фазу индуктивность и/или емкость), называется комплексным сопротивлением или импедансом.
Итак, антенна – это проводник, к которому подводится электрическая энергия и который ее излучает в окружающее пространство. Излучает электрический ток в проводнике, который создает вокруг проводника магнитное поле.
Почему электромагнитная энергия выходит из комфортного для нее проводника в некомфортный для нее вакуум? А она и не выходит! Энергия создает колебания поля, но не движется сама по себе. Давайте сравним со звуковыми волнами. Когда динамик (антенна) создает колебания, воздух (эфир) не движется, ветер не возникает, но колебания распространяются в воздухе (эфире). Так же происходит и с электромагнитными волнами, разве что электромагнитная энергия распространяется не в воздухе, а в эфире. Позже, правда, выяснят, что предполагавшегося эфира не существует, и что земля тоже не плоская, а электромагнитное поле прекрасно себя чувствует и в вакууме но мы-то знаем, что эфир есть, а земля, конечно, не плоская, а немного выпуклая. То есть, еще раз, энергия не переносится вместе со средой (точнее с полем), а переносится за счет распространения волн в неподвижной в общем случае среде (в поле).
Антенна как колебательный контур. Прежде чем говорить о конкретных конструкциях простых антенн, по принципу устройства которых мы сможем разобраться и в устройстве сложных, поговорим об электрическом резонансе. Для этого вернемся назад к реактивному сопротивлению. Полотно антенны можно представить как распределенную емкость и распределенную индуктивность – как размотанную до прямого провода катушку и как вырожденные до того же самого провода пластины конденсатора. Наличие реактивного сопротивления в цепи, как мы помним, разделяет фазы тока и напряжения. Однако, если мы подберем определенную комбинацию индуктивности и емкости (а это сработает только на одной определенной частоте, ведь мы помним, что с изменением частоты меняется реактивное сопротивление), то получится, что емкость и индуктивность взаимно компенсируют друг друга и мы видим чисто активное сопротивление в нагрузке. Вот такая взаимная компенсация и результат в виде чисто активного сопротивления как результат компенсации называется электрическим резонансом. Сам по себе для работы антенны он неважен, потому что антенна, как мы уже выяснили, излучает током в проводнике. Однако, есть ряд причин, по которым к достижению резонанса в антенне стремятся. Дело в том, что в отличие от постоянного тока, для переменного важно, чтобы волновое сопротивление (напоминаю закон Ома, а именно что сопротивление цепи численно равно приложенному напряжению, деленному на ток) генератора, линии передачи и нагрузки, т.е. собственно антенны, были равны. Если равенства нет, часть электромагнитной энергии отразится назад на генератор, что приведет к целому спектру нежелательных явлений. Значительное реактивное сопротивление приводит к сильному рассогласованию и значительному отражению энергии. Впрочем, это касается и активной компоненты импеданса, согласовать которую легче при незначительной, легко компенсируемой реактивной компоненте. Поэтому технически стараются создавать такие антенны, у которых реактивная компонента отсутствует или легко компенсируется, а активная равна волновому сопротивлению генератора или легко трансформируется. В случае самых простых антенн, создание определенной емкости антенны или определенной индуктивности означает попросту подбор размеров. Поэтому обычно размеры антенн меряют не в линейных единицах, а в долях длины волны.
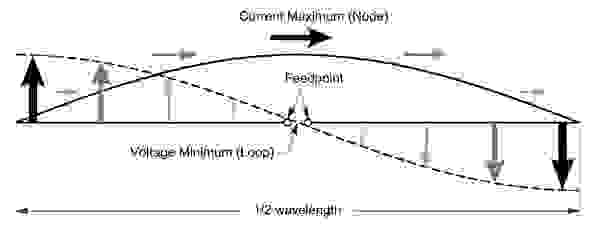
Простейшие полноразмерные антенны. Полуволновый диполь, четвертьволновый граундплейн и аналогичные конструкции.
Как видим, распределение токов и напряжений одинаково. Только если в четвертьволновом граундплейне одна половина диполя — штырь, а второй половиной является земля, то в полуволновом диполе — второй половиной является его вторая половина. 🙂
Для ознакомления с принципами, одинаковыми для любых более сложных антенн, предлагаю разобраться с устройством и работой базовых антенн – симметричного полуволнового диполя или несимметричного четвертьволнового граундплейна. В известной степени они идентичны и полуволновый диполь можно рассматривать как крайний случай четвертьволнового граундплейна, угол радиалов (противовесов) которого достиг 180° к излучающему штырю, поэтому большинство рассматриваемых особенностей в равной мере применимы к обоим антеннам.
Как видим, такая антенна имеет электрический резонанс, потому что в ее проводнике помещается целое число полуволн тока и целое число полуволн напряжения. Они смещены по фазе друг относительно друга, но их реактивность взаимно компенсируется.
Если бы антенна была немного короче, чем полволны, то у нее бы появилась емкостная компонента импеданса и ее пришлось бы компенсировать индуктивностью (никому не напоминает катушки в основании сибишных автоантенн?), а если наоборот удлинить, то появится индуктивная компонента, которую необходимо скомпенсировать емкостью.
Сопротивление излучения. В сопротивлении излучения нет ничего особенного. Вернее не так. Сопротивления излучения в физическом смысле не существует, это аналитическое значение, которое используется для определения КПД антенны. Проще всего представить себе сопротивление излучения как ту активную компоненту полного сопротивления всей антенны, которая тратится на излучение. Вообще-то есть термин «потери на излучение» и это полезные «потери», если мы говорим об антенне, но это не равно сопротивлению излучения, так что не путайте. Нет никакого воображаемого сопротивления среды воображаемому излучению в нее или что либо еще — есть разные свойства вроде диэлектрической проницаемости, которые мы рассматривать пока что не будем.
Еще в антенне есть сопротивление потерь в виде сопротивления проводника, которое тратится на его нагрев, различные потери в конструктивных элементах и согласующих звеньях. Знание сопротивления излучения необходимо для понимания КПД антенны: у некоторых антенн сопротивление излучения может составлять единицы и доли Ома при том, что сопротивление потерь в разы больше, что значит что КПД такой антенны крайне низок несмотря на то, что в остальном ее конструкция адекватна. В простых антеннах вроде рассматриваемого диполя или граундплейна, сопротивление излучения близко к полному сопротивлению самой антенны, потому что потери в проводнике сравнительно малы, но в любом случае это не тождественные понятия.
Вернемся к диполю. Пока мы подаем энергию в его геометрическом центре, где ток максимален, а напряжение минимально, сопротивление излучения невелико. Теоретически оно равно приблизительно 73 Омам, а практически немного меньше в зависимости от относительной толщины материала. По мере расщепления одной из половин диполя на отдельные радиалы, сопротивление будет немного снижаться и упадет до приблизительно 36 Ом ми угле в 90° к штырю. Это очевидно влияет на КПД антенны. Но, для наглядности, будем рассматривать именно диполь. По мере смещения точки питания от центра к краю мы увидим, что ток падает, а напряжение растет, то есть растет сопротивление излучения, которое достигнет своего максимума при питании с конца. На все остальные характеристики антенны это обстоятельство не влияет, она по-прежнему излучает с той же диаграммой направленности, а значит, имеет ту же эффективность излучения (но не КПД всей антенны в сборе, потому что КПД зависит от относительных потерь).
Полное сопротивление антенны равно напряжению в точке питания, деленному на отдаваемый ток. А состоит оно из, как мы уже выяснили, сопротивления излучения, на котором мы полезно теряем энергию на нужное нам излучение, и сопротивления потерь, на котором мы теряем энергию бесполезно. Разными способами мы можем влиять на полное сопротивление антенны. Не меняя геометрию, мы можем смещать точку питания. Мы можем использовать различные трансформирующие элементы (включая буквально трансформаторы с обмотками на тех частотах, на которых их применение рационально). На эффективность излучения антенны все эти манипуляции никак не влияют и нужны только для согласования антенны с генератором (передатчиком). Например, полуволновый диполь с питанием по центру, сопротивление которого составляет приблизительно 73 Ома, через простой трансформатор 1:4 может быть согласованным с генератором, рассчитанным на антенну сопротивлением 18 Ом или 300 Ом — смотря как подключить выводы. На работе антенны это не скажется никак, кроме влияния потерь в трансформаторе на КПД всей конструкции в сборе.
Если вам кажется, что у антенны есть только монополь – некий штырь, кусок провода или просто дорожка на печатной плате, то на самом деле это вариант граундплейна, у которого нет специально выделенных радиалов, но радиалами служит земля, тело оператора (портативной радиостанции, например) или земляные полигоны на плате. Потери в таких радиалах очевидно больше, чем в специально созданных как часть антенны, поэтому КПД таких конструкций всегда ниже, равно как и степень согласования импедансов из-за непредсказуемости ситуативных вместо расчетных радиалов.
При увеличении длины антенны сверх полуволнового диполя сопротивление излучения сначала растет, достигая максимума при четном числе полуволн, а затем снова падает, достигая минимума при нечетном числе полуволн. Незначительное увеличение длины сужает диаграмму направленности и увеличивает эффективность передачи в выбранном направлении, а значительное приводит к дроблению диаграммы на множество лепестков и в целом неэффективно, поэтому на практике обычно не применяется кроме многодиапазонных антенн, в которых это является компромиссным решением.
Вообще любое увеличение длины диполя сверх половины волны приводит к тому, что на полотне возникают области, где ток течет в противоположном направлении. Этот ток, разумеется, также участвует в излучении, но интерференция создаваемого им поля с полем условно-основной части полотна и приводит к тому, что диаграмма направленности расщепляется, что в большинстве случаев вредно: обычно радиосвязь производится по одному или нескольким известным направлениям а излучение в «ненужную» сторону означает просто напрасные потери. Например, наземная связь проводится в направлении горизонта, а излучение в космос бесполезно тратит мощность передатчика. Поэтому, когда необходимо увеличить направленность антенны, чтобы посылать энергию более сфокусировано в нужном направлении, предпочитают использовать более сложные конструкции на базе диполя, а не удлиняют единичный диполь.
При уменьшении длины антенны от полуволнового диполя (или укорочению штыря четвертьволнового граундплейна) сопротивление излучения экспоненциально падает, что вкупе со все усложняющимся согласующим устройством делает укороченную антенну крайне неэффективной – небольшое сопротивление излучения рядом с большим сопротивлением означает напрасный нагрев согласующего устройства с малым излучением.
Вот, собственно, и все, что нужно знать гуманитарию об антеннах.
Калькулятор волнового сопротивления коаксиального кабеля
Полезный инструмент для расчета волнового сопротивления (импеданса) коаксиальных линий передачи (кабелей, фидеров и пр.).
Расчет
Входные данные:
Результаты:
Обзор
Коаксиальный кабель, наряду с симметричным двухпроводным кабелем, является наиболее распространенным типом линий передачи, используемой в радиосвязи. Данный калькулятор поможет вам рассчитать волновое сопротивление (импеданс) коаксиального кабеля с учетом его размеров. Он также предоставит временную задержку вносимую кабелем в сигнал, а также погонные емкость и индуктивность.
Примечание: внутренний диаметр экрана всегда больше диаметра внутреннего проводника.
Формулы
Волновое сопротивление (импеданс):
Применение
Коаксиальный кабель является, пожалуй, наиболее широко используемым типом линии передачи. Он состоит из твердого центрального проводника, окруженного диэлектрическим материалом, обычно пластиковым изолятором, таким как фторопласт. Также возможно использование воздушного или газового диэлектрика, в котором центральный проводник удерживается на месте повторяющимися проставками. Над изолятором находится второй проводник, цилиндрическая оплетка или экран, выполненный из тонких проволок. Внешняя пластиковая оболочка защищает и изолирует оплетку.
Основным преимуществом коаксиального кабеля является то, что он полностью экранирован, поэтому внешний шум практически на него не влияет. Коаксиальные кабели – это не симметричные линии; ток в центральном проводнике привязан к экрану, который заземлен. Коаксиальные кабели обеспечивают значительную, но не полную защиту от шумовых помех и перекрестных помех, вызванных внешними сигналами из-за индуктивных и емкостных связей. Неэкранированные линии, напротив, могут принимать сигналы и перекрестные помехи и даже излучать энергию, что приводит к нежелательным потерям сигнала.
Волновое сопротивление (импеданс) коаксиальных кабелей необходимо знать, потому что для максимальной передачи мощности необходимо согласовывать импеданс кабеля с тем местом, к которому он подключен (будь то передатчик или антенна). Коаксиальные кабели обычно имеют более низкое волновое сопротивление по сравнению с симметричными линиями и дипольными антеннами. В этом случае для согласования между ними часто используется симметрирующий трансформатор (англ. «balun» от «balanced to unbalanced»).