Как посчитать вероятность пересечения событий
Вероятность произведения (пересечения) событий. Независимость событий.
Из определения условной вероятности (формулы (1) и (2)) следует, что
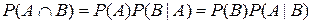
т.е. вероятность пересечения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.
Равенство (3) называется правилом или теоремой умножения вероятностей. Его можно обобщить на случай n событий:
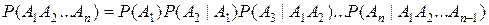
Так для трех событий А1, А2, А3 получаем
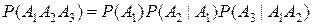
Пример. На 7 карточках написаны буквы л, л, о, о, о, т, т. Из них последовательно выбираются 4 и кладут слева направо. Найдем вероятность того, что в результате образуется слово «лото» (событие А).
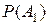
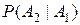
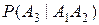
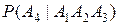
Определение 1. События А называется независимым от события В, если условная вероятность события А при условии события В совпадает с безусловной вероятностью события А, т.е. Р(А| В)=Р(А). Если событие А не зависит от события В, то и событие В не зависит от события А.
Определение 2. События А и В называются независимыми, если появление одного из них не меняет появления другого. В противном случае события А и В называются зависимыми.
Для независимых событий теорема умножения имеет вид: Р(АВ)=Р(А)Р(В).
Определение 3. События А и В называются независимыми, если вероятность их совместного появления равна произведению их вероятностей, т.е.
Если же это равенство не выполняется, то события А и В называются зависимыми.
Если события А и В независимы, то независимы и пары событий 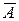
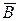
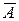
На практике о независимости тех или иных событий часто судят исходя из интуитивных соображений и анализа условий опыта, считая независимыми события, между которыми нет причинно-следственных связей.
Понятие независимости может быть распространено на случай п событий.
Определение 4. События А1, А2,…, Ап называются независимыми в совокупности (независимыми), если каждое из них не зависит от произведения любого числа остальных событий и от каждого в отдельности. В противном случае события А1, А2,…, Ап называются зависимыми.
Для независимых событий их условные вероятности равны безусловным и формула (4) имеет вид
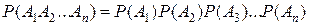
Из независимости событий А1, А2,…, Ап в совокупности вытекает их попарная независимость (любые два из них независимы). Однако из попарной независимости, вообще говоря, независимость в совокупности не следует.
Пример. Производится выбор наудачу флага из четырех имеющихся в наличии: красного, голубого, белого и трехцветного (красно-бело-голубого). Исследовать на независимость события: А=<выбранный флаг содержит красный цвет>, В=<выбранный флаг содержит голубой цвет>, D=<выбранный флаг содержит белый цвет>.
Решение. Возможных исхода выбора 4; Событию А благоприятствует 2 исхода (красный цвет содержится в двух флагах). Поэтому Р(А)=2/4=1/2. Аналогично находим, что Р(В)=Р(D)=1/2. Событию 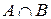
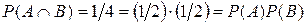
Дата добавления: 2016-03-04 ; просмотров: 6079 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
МАТЕМАТИКА
Продолжаем разбирать задачи по теории вероятностей из тестов ЕГЭ. Рассмотренные ранее в части 1 (простые задачи) и в части 2 (простые задачи на подбрасывание монеты и кубика) дают нам возможность немного углубиться в данную тему. Итак, сегодня рассмотрим объединение, пересечение событий и задачи о пересечении независимых событий.
При решении таких задач необходимы формулы вероятности для объединения несовместных событий и пересечения независимых событий. Также мы разберем несложные задачи, связанные с частотой и процентами.
Теоретическая часть
Два события А и В называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию А, так и событию В.
Например, при бросании кубика события «выпало число 3» и «выпало чётное число» несовместны. При этом события «выпало число больше 3-х» и «выпало чётное число» совместны.
Пусть событие С означает, что произошло хотя бы одно из событий А и В. Тогда С называют объединением событий А и В, пишут С = А U В (также объединение событий иногда называют суммой событий и обозначают А + В).
Если события А и В несовместны, то вероятность их объединения равна сумме вероятностей событий А и В:
Два события А и В называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.
Например, выполним последовательно два подбрасывания монеты. Тогда события «при первом подбрасывании выпала решка» и «при втором подбрасывании выпал орёл» являются независимыми: вероятность каждого из них равна 
Рассмотрим другой пример. Пусть в урне находятся два чёрных и два белых шара. Сперва из урны наугад извлекают один шар. Затем из той же урны наугад извлекают ещё один шар. Обозначим через А событие «первый извлечённый шар белый», а через В – «второй извлечённый шар чёрный». Тогда события А и В являются зависимыми. Действительно, если событие А произошло, то в урне из трёх оставшихся шаров два чёрных и Р(В) = 

Пусть событие С означает, что произошло как событие А, так и В. Тогда С называют пересечением событий А и В, пишут
(также пересечение событий иногда называют произведением событий и обозначают А • В).
Если события А и В независимы, то вероятность их пересечения равна произведению вероятностей событий А и В:
Также в условиях задач могут присутствовать проценты. Следует вспомнить, что 1 % – это 
Частотой события А называют отношение
, где n — общее число испытаний, m – число появлений события А.
Например, пусть мы подбросили монету 100 раз, орёл выпал 47 раз. Тогда частота выпадения орла в нашем эксперименте равна 
Задачи о пересечении независимых событий
Задача 3.1. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Н. с вероятностью 0,45. Если А. играет чёрными, то А. выигрывает у Н. с вероятностью 0,4. Гроссмейстеры А. и Н. играют две шахматные партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Обозначим события: W = «А. выиграл белыми», В = «А. выиграл чёрными». По условию, P(W) = 0,45, Р(В) = 0,4. Необходимо найти вероятность пересечения событий W и В, то есть 
Задача 3.2. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,4. Найдите вероятность того, что в случайный момент времени все три продавца заняты (считайте, что клиенты заходят независимо друг от друга).
Обозначим через А1, А2, А3 события, означающие, что в выбранный момент времени соответствующий продавец занят. По условию Р(A1) = Р(А2) = Р(А3) = 0,4. Искомая вероятность равна
Задача 3.3. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Здесь удобно сначала найти вероятность события «оба автомата неисправны», противоположного событию из условия задачи. Обозначим через А и В события «первый автомат неисправен» и «второй автомат неисправен». По условию Р(А) = Р(В) = 0,1. Событие «оба автомата неисправны» – это 
Искомая вероятность равна 
Задача 3.4. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые два раза попал в мишени, а последние три — промахнулся. Результат округлите до сотых.
Обозначим через А1, А2, А3, А4, А5 события, означающие попадание в мишень при соответствующем выстреле. По условию Р(A1)=Р(А2)=Р(А3)=Р(A4)=Р(А5)=0,6. Нам необходимо найти вероятность
Так как рассматриваемые события независимы, то эта вероятность равна


Что приблизительно равно 0,02.
Задача 3.5. На рисунке изображён лабиринт. Мышка заползает в лабиринт в точке «Вход». Развернуться и идти назад мышка не может, поэтому на каждом разветвлении мышка выбирает один из путей, по которому ещё не шла. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью мышка придёт к выходу В.
Расставим на перекрёстках стрелки в направлениях, по которым может двигаться мышка (см. рис. 2). Выберем на каждом из перекрёстков одно направление из двух возможных и будем считать, что при попадании на перекрёсток мышка будет двигаться по выбранному нами направлению.
Чтобы мышка достигла выхода В, нужно, чтобы на каждом перекрёстке было выбрано направление, обозначенное сплошной линией. Всего выбор направления делается 4 раза, каждый раз независимо от предыдущего выбора. Вероятность того, что каждый раз выбрана сплошная стрелка, равна
Итак, теперь вы знаете необходимые формулы вероятности для объединения несовместных событий и пересечения независимых событий, а также научились решать задачи о пересечении независимых событий.
После изучения материала по решению задач по теории вероятностей рекомендую выполнить задачи для самостоятельного решения, которые мы публикуем на нашем канале Telegram. Вы также можете проверить правильность их выполнения, внеся свои ответы в предлагаемую форму.
Также рекомендую изучить «Задачи на вычисление», урок «Площадь сектора» и другие уроки по решению заданий ЕГЭ по математике, которые представлены на нашем канале Youtube.
Спасибо, что поделились статьей в социальных сетях
Источник «Подготовка к ЕГЭ. Математика.Теория вероятностей». Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
Пересечение независимых событий
Теория вероятностей
Классическое определение вероятности.
Вероятностью события A называется отношение числа благоприятных для A исходов к числу всех равновозможных исходов: Р (А) = 
Противоположные события
Событие, противоположное событию A, обозначают Ā. При проведении испытания всегда происходит ровно одно из двух противоположных событий
Объединение несовместных событий
Два события A и B называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию A, так и событию B.
Если события A и B несовместны, то вероятность их объединения равна сумме вероятностей событий A и B: P(A U B) =P(A) + P(B)
Пересечение независимых событий
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.
Событие C называют пересечением событий A и B (пишут C = A∩B), если событие C означает, что произошли оба события A и B.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей событий A и B: P(A∩B) = P(A) • P(B)
Формула сложения вероятностей совместных событий:
P(A U B) =P(A) + P(B) – P(A∩B)
1. Из 1000 собранных на заводе телевизоров 5 штук бракованных. Эксперт проверяет один наугад выбранный телевизор из этой 1000. Найдите вероятность того, что проверяемый телевизор окажется бракованным.
2. В урне 9 красных, 6 жёлтых и 5 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
3. Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
4. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
5. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
6. На каждые 1000 электрических лампочек приходится 5 бракованных. Какова вероятность купить исправную лампочку?
7. В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
8. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?
9. На турнир по шахматам прибыло 26 участников в том числе Коля и Толя. Для проведения жеребьевки первого тура участников случайным образом разбили на две группы по 13 человек. Найти вероятность того, что Коля и Толя попадут в разные группы.
10. В классе 16 учащихся, среди них два друга —Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.
11. В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.
12. Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 спортсменов, среди которых 7 участников из России, в том числе Платон Карпов. Найдите вероятность того, что в первом туре Платон Карпов будет играть с каким-либо спортсменом из России?
13. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России?
14. В классе 26 учащихся, среди них два друга — Сергей и Андрей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Сергей и Андрей окажутся в одной группе.
15. В классе 21 ученик, среди них 2 друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Тоша и Гоша попали в одну группу.
17. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.
18. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 6, но не дойдя до отметки 9 часов.
При решении задач с монетами число всех возможных исходов можно посчитать по формуле п=2ª, где α –количество бросков
19. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орел выпадет ровно 1 раз.
20. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.
21. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл не выпадет ни разу.
22. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
23. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что решка не выпадет ни разу.
24. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.
25. Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.
26. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
27. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
28. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
29.Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
30. В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
Артём Санников
Языки программирования
Базы данных
Программное обеспечение
Операционные системы
Мобильная разработка
Менеджеры пакетов
Сетевые технологии
CMS системы
Математика
SEO продвижение
Социальные сети
Психология
Хостинг провайдер
Смартфоны
Операции над событиями. Теория вероятностей
Пересечение событий
Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.
События не пересекаются
Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.
События пересекаются
Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.
Объединение событий
Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.
События не пересекаются
Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).
События пересекаются
Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)
Независимые события
События A и B независимы, если наступление одного события не влияет на другое событие.
Практический пример
Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:
Событие A: выпало > 3 очков
Событие B: выпало нечетное число очков
Чтобы приступить к решению задачи выполняем анализ событий.
Анализ события A: этому событию соответствует три элементарных исхода
Анализ события B: этому событию соответствует три элементарных исхода
После анализа событий приступаем к пошаговому решению.
Отсюда мы можем посчитать вероятность этого события:
Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:
Другие статьи из категории «Теория вероятностей»
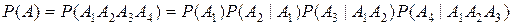


 (также пересечение событий иногда называют произведением событий и обозначают А • В).
(также пересечение событий иногда называют произведением событий и обозначают А • В). , где n — общее число испытаний, m – число появлений события А.
, где n — общее число испытаний, m – число появлений события А.





