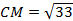Как посчитать угол зная косинус
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
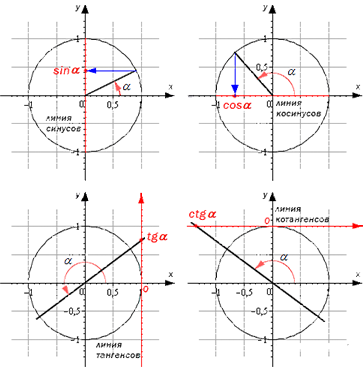
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
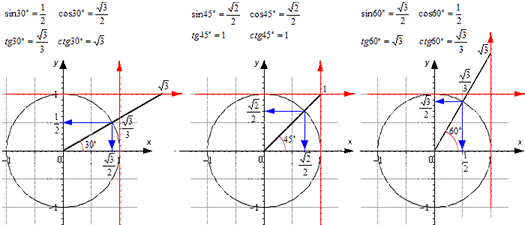
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Сведение к углу
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Таблица косинусов
Содержание статьи
Таблица косинусов –
это удобное решение для проведения быстрых расчетов, когда нужно получить числовое значение косинуса того или иного угла. В статье мы узнаем, что такое косинус, чем похожи и как связаны таблица синусов и косинусов, как использовать таблицу синусов Брадиса для получения конкретных числовых значений косинуса того или иного угла.
Что такое косинус угла и как его применять в решении задач
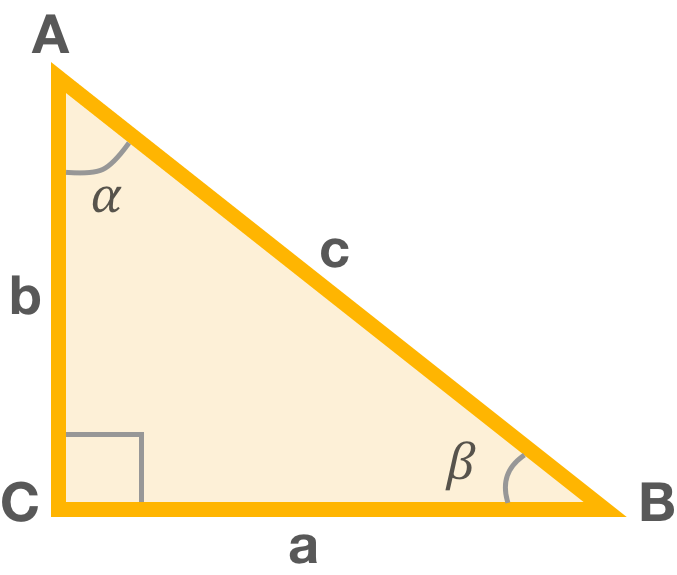
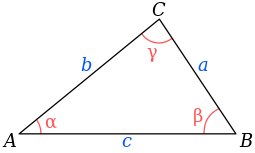
Прямой угол всегда равен 90°, острый – всегда меньше, а тупой – больше 90°
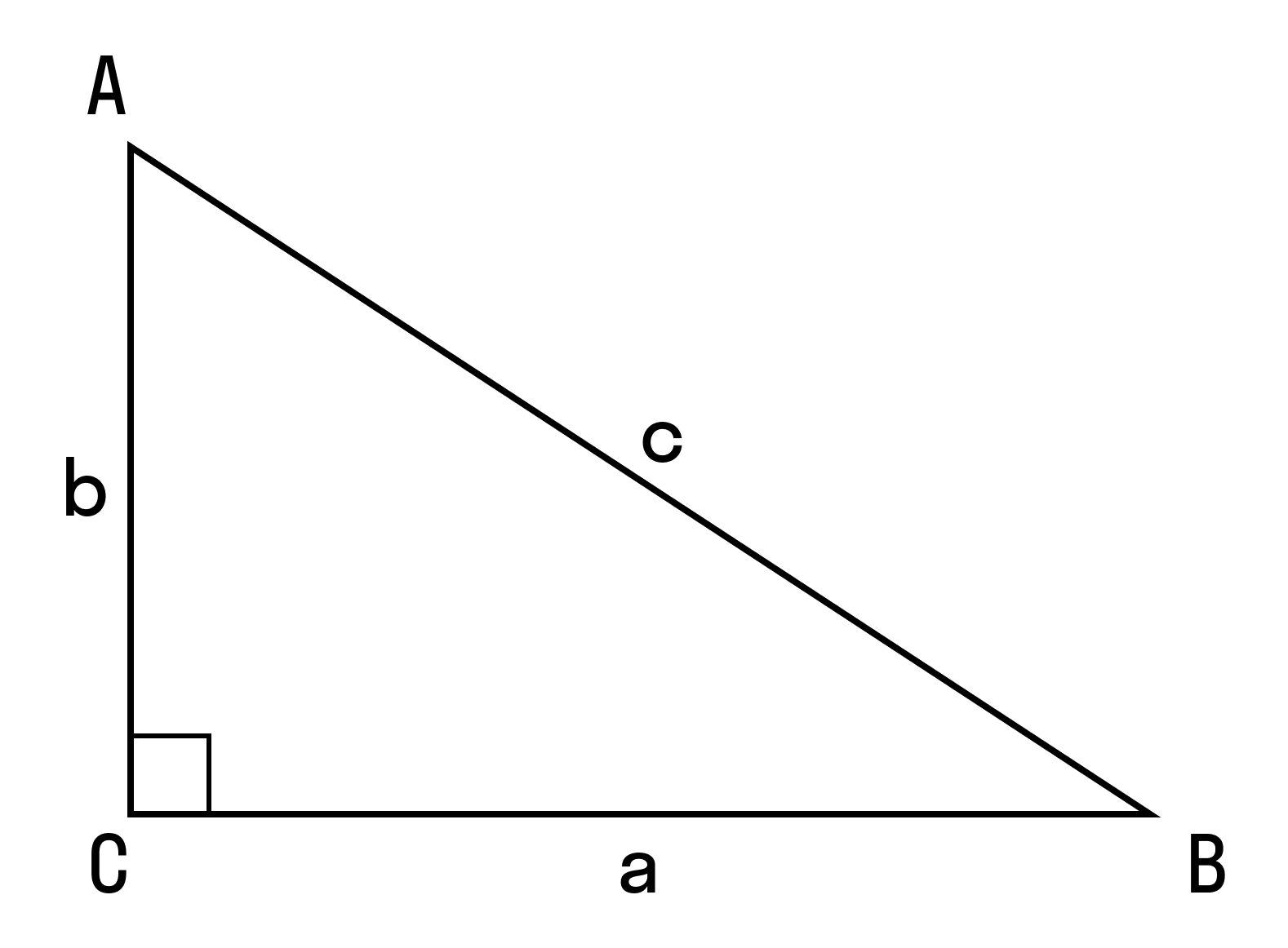
Согласно теореме косинусов, что бы рассчитать угол α или β, нужно знать длину гипотенузы (АВ) и прилежащий к этому углу катет.
Косинус – это отношение прилежащей стороны к гипотенузе:
То есть, если вам нужно узнать, например, какой высоты делать крышу над домом, если известна ширина дома и угол наклона крыши, что бы снег не задерживался, то высоту конька рассчитать не составит труда, применяя теорему косинусов. Нужно помнить, что такие функции, как косинусы и синусы в формулах зависят от угла. Синус работает с противолежащей стороной, косинус с работает прилежащей.
Это тригонометрические формулы для вычисления углов в треугольнике через тригонометрические функции синус, косинус, тангенс, котангенс
Косинус – отношение прилежащего катета к гипотенузе
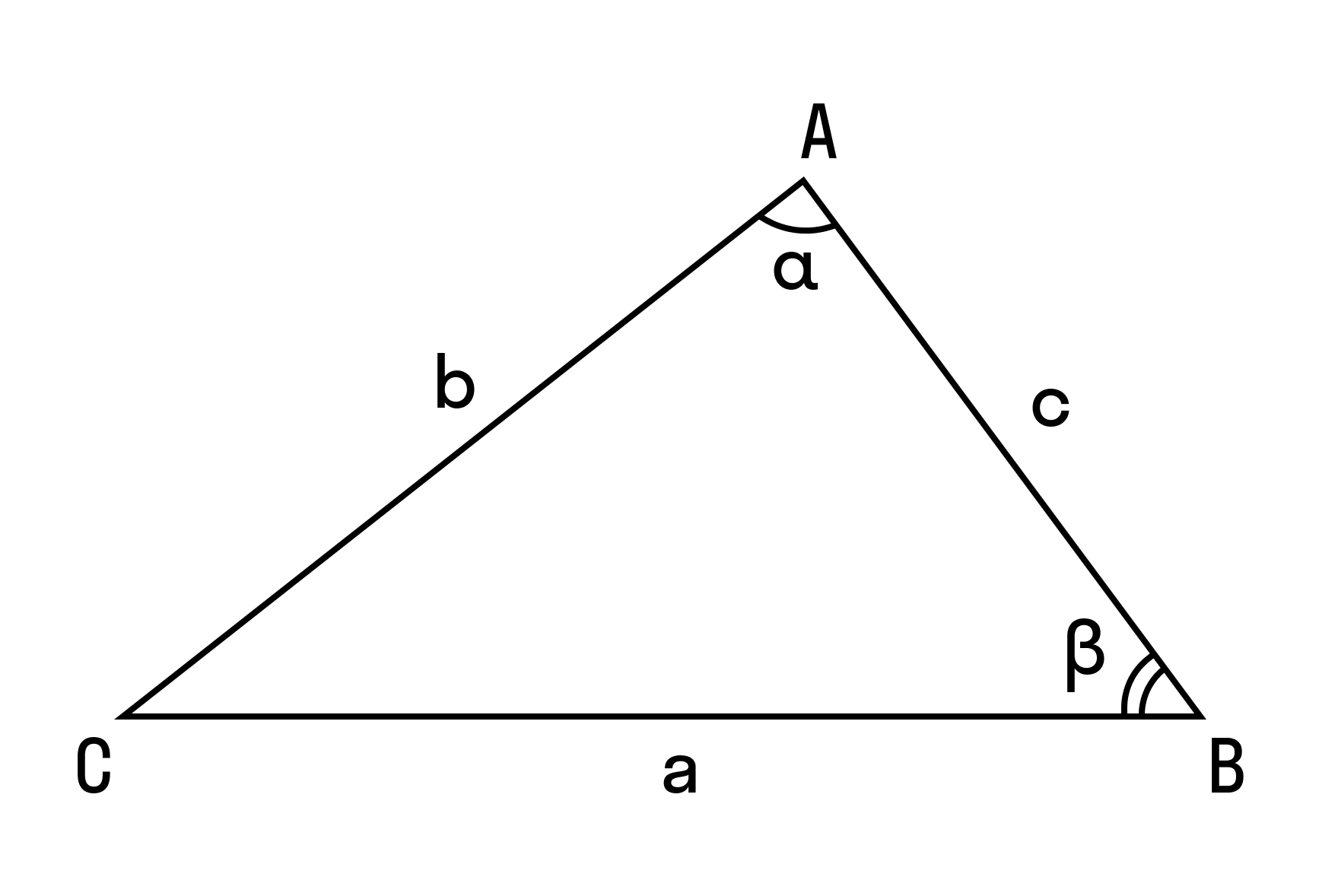
Если треугольник не прямоугольный, его параметры также можно рассчитать, используя теорему Евклида. Суть ее в том, что треугольник, лежащий на плоскости, и имеющий стороны а, b, с, а также углом α, который находится напротив стороны а, может быть рассчитан по следующей формуле:
Отсюда можем найти cos α, cos α =( b²+2²- а²) : 2bс.
Ниже приведена таблица косинусов, дополнительно указаны синусы в их числовом выражении.
| Значение угла α (градусов) | Значение угла α в радианах | COS (косинус) |
|---|---|---|
| Косинус 0 градусов | 0 | 1 |
| Косинус 15 градусов | π/12 | 0.9659 |
| Косинус 30 градусов | π/6 | 0.866 |
| Косинус 45 градусов | π/4 | 0.7071 |
| Косинус 50 градусов | 5π/18 | 0.6428 |
| Косинус 60 градусов | π/3 | 0.5 |
| Косинус 65 градусов | 13π/36 | 0.4226 |
| Косинус 70 градусов | 7π/18 | 0.342 |
| Косинус 75 градусов | 5π/12 | 0.2588 |
| Косинус 90 градусов | π/2 | 0 |
| Косинус 105 градусов | 5π/12 | -0.2588 |
| Косинус 120 градусов | 2π/3 | -0.5 |
| Косинус 135 градусов | 3π/4 | -0.7071 |
| Косинус 140 градусов | 7π/9 | -0.766 |
| Косинус 150 градусов | 5π/6 | -0.866 |
| Косинус 180 градусов | π | -1 |
| Косинус 270 градусов | 3π/2 | 0 |
| Косинус 360 градусов | 2π | 1 |
Калькулятор расчета косинуса онлайн
Примеры решения задач по геометрии по нахождению неизвестных величин с применением таблицы косинусов Брадиса
Пример 1: Для примера решим следующую задачу. Берем прямоугольный треугольник, у него нужно найти оба угла, но известны гипотенуза с = 12 см, сторона b = 9,2 см. По теореме косинусов
cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.
Но наше значение меньше табличного на 0,0006, что становит 3′. Тогда мы вычитаем эту поправку 3′, 39°54′ – 3′ = 39°51′. Второй угол находим, исходя из того, что сумма всех углов в треугольнике не должна превышать 180°. Поэтому 180° – (90° + 39°51′) = 50° 09′. Угол β = 50° 09′. Решаем задачу дальше. Ищем сторону а. Для этого мы можем использовать два способа.
Второй вариант немного проще в вычислении. Обращаемся к таблице Брадиса снова. У нас ближайшее значение 50° 06′ = 0,6414. Поправка на 3′ составляет 0, 0007. Тогда 0, 6414 + 0,0007 = 0,6421.
Пример 2: Рассмотрим треугольник с произвольными углами, ни один из которых не равен 90°. Мы имеем две стороны с =12 см, b = 8,2 см, а также угол α, который равен 31°12′. Найти третью сторону. Формула, которая применялась в предыдущей задаче, не подходит, так как у нас треугольник не прямоугольный (по крайней мере мы это ещё не рассчитали). Используем формулу из теоремы косинусов:
а² = b²+с²-2²· b· cos α. Косинус угла находим на пересечении угла 31° и 12′. Он равен числу 0,8554, которое мы и подставляем в формулу.
Если будет стоять задание найти ещё и углы треугольника, используем формулу:
с² = а² + b² – 2аb cos γ, отсюда cos γ = (b² + а² – с²): 2 bс. cos γ = (8,2² + 13,54² – 12²): 2· 8,2·12 = (64,24 + 183, 17 – 144): 196,8 = 0, 5255. Открываем таблицу Брадиса. Это число соответствует 58° 18′. Согласно теореме о правилах трёх углов в треугольнике находим третий угол:
180° – 58° 18′-31°12′ =89° 30′. Задача решена!
Можно не рассчитывать самому, а использовать сервис и высчитать косинус онлайн, когда регистрируешься на сайте, и любое вычисление приходит автоматически. Минус такого сервиса, его нельзя применять на экзамене по математике. В качестве справочного материала таблицы предоставляются. Естественно, надо хорошо уметь ими пользоваться, так как на экзамен отводится ограниченное количество времени.
Теорема косинусов и синусов
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
В статье мы расскажем, как находить значения:
Как вычисляются синусы и косинусы углов?
Предположим, стоит задача найти косинус и синус угла \(30^°\). Отложим на круге угол в \(30^°\) и найдем какая точка соответствует этому углу.
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают \(0,1\); \(0,2\); \(0,3\) и т.д., а сразу наносят стандартные значения для синуса и косинуса: \(±\frac<1><2>=±0,5\); \(±\frac<\sqrt<2>> <2>≈±0,707\); \(±\frac<\sqrt<3>> <2>≈±0,866\).
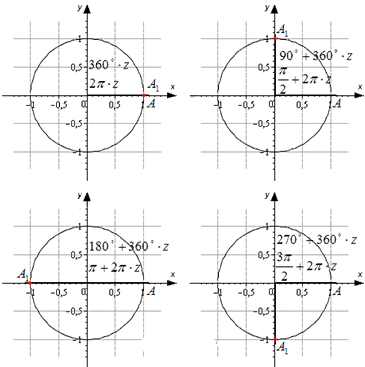
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
Градусная мера окружности равна \(360^°\), полуокружности \(180^°\), а четверти \(90^°\);
Углы в \(0^°\), \(30^°\), \(45^°\) и \(60^°\) выглядят так:
Задание 1 . Отметьте на окружности точки соответствующие углам: \(720^°\), \(225^°\), \(300^°\), \(870^°\), \(900^°\), \(-330^°\), \(-630^°\), \(-210^°\).
Как находить синус и косинус любого угла?
\(-540^°\) на тригонометрическом круге совпадает с \(-1\) на оси косинусов. То есть, координаты этой точки: \((-1;0)\). Значит, \(\cos(-540^°)=-1\), а \(\sin(-540^° )=0\).
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).
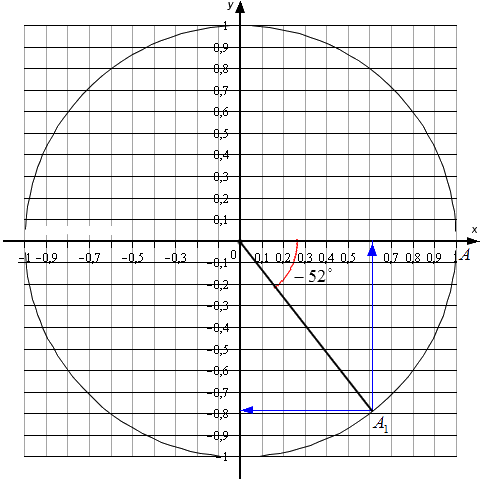
Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения \(54\sqrt<3>\cos(510^°)\).
Решение. \(510^°=360^°+150^°=360^°+180^°-30^°.\)
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
В статье мы расскажем, как находить значения:
Как вычисляются синусы и косинусы углов?
Предположим, стоит задача найти косинус и синус угла \(30^°\). Отложим на круге угол в \(30^°\) и найдем какая точка соответствует этому углу.
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают \(0,1\); \(0,2\); \(0,3\) и т.д., а сразу наносят стандартные значения для синуса и косинуса: \(±\frac<1><2>=±0,5\); \(±\frac<\sqrt<2>> <2>≈±0,707\); \(±\frac<\sqrt<3>> <2>≈±0,866\).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
Градусная мера окружности равна \(360^°\), полуокружности \(180^°\), а четверти \(90^°\);
Углы в \(0^°\), \(30^°\), \(45^°\) и \(60^°\) выглядят так:
Задание 1 . Отметьте на окружности точки соответствующие углам: \(720^°\), \(225^°\), \(300^°\), \(870^°\), \(900^°\), \(-330^°\), \(-630^°\), \(-210^°\).
Как находить синус и косинус любого угла?
\(-540^°\) на тригонометрическом круге совпадает с \(-1\) на оси косинусов. То есть, координаты этой точки: \((-1;0)\). Значит, \(\cos(-540^°)=-1\), а \(\sin(-540^° )=0\).
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).
Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения \(54\sqrt<3>\cos(510^°)\).
Решение. \(510^°=360^°+150^°=360^°+180^°-30^°.\)
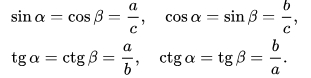
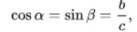 cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.
cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.