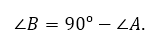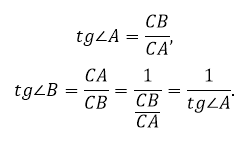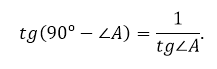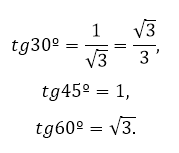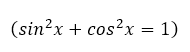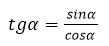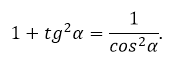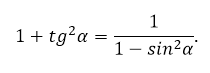Как посчитать угол по тангенсу
Математика для блондинок
Страницы
вторник, 9 октября 2012 г.
Как найти угол по тангенсу
В комментариях к тригонометрической таблице меня спросили, как перевести в градусы tg@= 4,99237? В общем виде вопрос заключается в том, как найти угол по тангенсу? Для решения этой задачи мы будем использовать калькулятор. Поскольку математики никогда не ставили перед собой задачи навести порядок в математике, то углы и сегодня измеряются в самых разных единицах измерения. Наиболее популярны среди математиков градусная и радианная меры углов. Мы тоже найдем решение как в градусах, так и в радианах. Благо, на калькуляторе они есть.
Как включить калькулятор? Читайте в конце этой страницы.
Сначала мы найдем угол по тангенсу в градусах. Для этого в правом верхнем углу калькулятора нужно установить специальный пыптик в положение Deg 360, что соответствует градусам. Дальше кнопочками вводим число 4,99237. Вот что у нас должно получиться.
После этого нужно нажать кнопочку арктангенс. Именно эта математическая ерунда превращает значение тангенса в угол. На калькуляторе эта хитрая обратная тригонометрическая функция (как её величают математики) замаскирована под кнопочку tan в степени минус 1, то есть тангенс в минус первой степени. После нажатия этой кнопочки восторженный калькулятор на все лады расхваливает нашу мудрость и всеми возможными способами сообщает нам, что мы таки ковырнули арктангенс, а не что нибудь другое. Об этом свидетельствует название функции atan (4.99237) в окошке калькулятора. Для особо одаренных здесь же буковками написано Arc tangent. Правда, особо одаренным нужно ещё знать английский язык, для того, чтобы понять всю глубину восторга калькулятора.
Для полного счастья, можно пролить бальзам на душу математиков, разложив эту десятичную форму записи градусов на градусы, минуты и секунды. Для этого дробную часть числа умножаем на 60 и получаем количество минут в дробном хвосте градусов.
Подобную процедуру повторяем с минутами. Дробную часть минут умножаем на 60 и получаем секунды.
Процедуру можно повторять и дальше до бесконечности, но, к счастью, математики до этого ещё не додумались. По этому на секундах мы и остановимся. Ничего, что секунды у нас получились с дробным хвостиком. Математики к таким хвостам относятся терпимо. В итоге, полнометражная версия полученного нами угла в градусной мере углов выглядит следующим образом:
78 градусов 40′ 23,52″
В слух эта магическая надпись произносится так: «78 градусов, 40 минут, 23 целых и 52 сотых секунды». Аминь!
Нет, ещё не «Аминь!». Теперь нужно выковырять из калькулятора этот же угол, только в радианах. Процедура добывания угла точно такая же, как и для градусов, с той только разницей, что в самом начале мы на калькуляторе нажимаем соседний пыптик Rad 2п. Повинуясь нашей воле, калькулятор добросовестно выдаст нам результат в радианах. Вот как это будет выглядеть.
Как видите, в радианах мы получили всего-навсего 1,3731 радиан. И за что математики так любят радианы? Ведь, плюнуть не на что. Ну, да Бог с ними, с этими математиками.
Тетерь самый интересный вопрос из комментариев: «А как включить-то калькулятор. «
Теритически, на всех компьютерах и смартфонах калькулятор устанавливается по умолчанию. Просто его нужно найти.
Компьютер. Нажимаем кнопку «Пуск», затем нажимаем «Все программы». Ищем среди программ «Стандартные» и открываем эту папку. У меня именно в ней спрятана программа «Калькулятор». Открываем эту программу нажатием левой кнопки мыши, появляется калькулятор. Если вы не видите на калькуляторе тангансов, котангенсов и прочей математической ерунды, тогда в верхнем меню нажмите на слово «Вид» и включите пиптик «Инженерный». Ваш калькулятор готов к великим математическим свершениям. Кстати, по логике разработчиков калькуляторов, вся эта математическая ерунда типа тангенсы-котангенсы обычным людям и даром не нужна, о чем всидетельствует «Обычный» вид калькулятора.
Смартфон. У меня калькулятор расположен прямо на главном экране. Нажимай и пользуйся. Вот только вылезает калькулятор в обычном виде. Где найти математику? Никогда не задавался таким вопросом. Методом научного тыка выяснил, что в левом нижнем углу экрана есть красненький значек, изображающий два какдратика по диагонали и две стрелочки. После нажатия на этот символ появляются все математические фишки, заложенные разработкичами. Теперь вы становитесь повелителем тангенсов-котангенсов и прочих математических чудес.
Калькулятор тангенса
Тангенс — тригонометрическая функция, численно равная соотношению длин противолежащего и прилежащего катета. Тангенс широко используется во многих современных приложениях.
История вопроса
Тригонометрия берет свое начало в Древнем Вавилоне, когда ученые изучали свойства сторон прямоугольного треугольника. Именно тогда была сформулирована теорема, постулирующая соотношение катетов и гипотенузы, доказанная только через полторы тысячи лет самосским математиком Пифагором. Изначально использовался только синус, который рассчитывался как половина хорды окружности, описанной вокруг прямоугольного треугольника.
Тангенс появился гораздо позднее, когда перед учеными возникла задача определения длины тени, отбрасываемой объектами, стоящими перпендикулярно к поверхности земли. Тангенс был введен арабским математиком Абу-ль-Вафой в десятом веке. Восточный ученый составил специальные таблицы для определения тангенсов и котангенсов, однако это открытие так и не попало на европейский континент.
В Европе тангенсы были вновь открыты только в XIV веке: немецкий математик Иоганн Мюллер Региомонтан использовал функцию в астрономических расчетах. Термин «тангенс» произошел от латинского слова tanger, что означает «касание» и был введен в обиход в конце XVI века. Данный термин использовался для описания линии тангенсов, то есть касательной к единичной окружности. Региомонтан доказал теорему тангенсов, а также составил специальные таблицы значений функции, которые подошли как для плоской, так и для сферической геометрии.
Определение тангенса
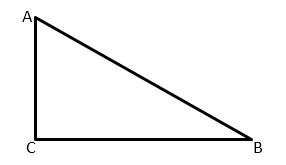
Геометрически тангенс определяется как соотношение противолежавшего катета к прилежащему. Функция всегда рассчитывается для угла и не зависит от длин сторон. Пусть у нас есть треугольник со сторонами A, B и C, где C — гипотенуза. Тангенс угла AC будет рассчитываться как соотношение противолежащего катета B к прилежащему A или tgAC = B/A. Для угла BC тангенс рассчитывается как дробь, в числителе которой длина противолежащего углу катета A к прилежащему B, что математически записывается как tgBC = A/B. Угол AB образуется при двумя катетами, поэтому его невозможно посчитать. Катеты — стороны, образующие прямой угол, поэтому для угла в 90 градусов тангенс не существует.
Помимо геометрического определения, тангенс легко выразить через другие тригонометрические функции. Так, для угла A тангенс можно выразить при помощи отношения синуса и косинуса:
Наша программа позволяет определить численное значение тангенса для любого значения угла. Для этого достаточно выбрать в меню соответствующую функцию и ввести в ячейку «Угол» величину угла в градусах или радианах. Если необходимо найти угол по известному значению тригонометрической функции, используйте функцию арктангенса. Для этого введите значение тангенса в соответствующую ячейку, после чего калькулятор вернет вам величину угла.
Рассмотрим пару примеров
Вычисление угла
Пусть в школьной задаче задан прямоугольный треугольник со сторонами A = 5 см, B = 12 см, C = 13 см. Требуется найти величины всех углов. Итак, очевидно, что угол AB, то есть угол, образуемый двумя катетами — прямой. Это известно из самого определения катетов. Теперь мы можем найти тангенс угла BC, который численно будет равен дроби, в числителе которой противолежащий катет A, а в знаменателе — прилежащий B. Следовательно, tgBC = A/B = 5/12 = 0,416. Зная тангенс, мы легко можем вычислить соответствующий угол при помощи онлайн-калькулятора. Для это выберем в меню функцию тангенса и введем значение 0,416 в ячейку tgα. Программа мгновенно отобразит величину угла, равную 22,58 градуса. Вычислить последний угол не составит труда, так согласно постулату о сумме углов треугольника, угол AC = 180 − 90 − 22,58 = 67,42 градуса.
Вычисление тангенса
В школьных задачах чаще всего используются стандартные углы, поэтому школьникам важно знать значения основных тригонометрических функций для этих углов буквально наизусть. Давайте при помощи калькулятора определим значения тангенсов для наиболее распространенных в задачах углов:
Выше мы выяснили, почему тангенс не рассчитывается для значений 90 градусов. Еще одно интересное значение — угол в 45 градусов. Почему тангенс равен 1? Ответ очевиден, ведь если в прямоугольном треугольнике один угол равен 45 градусам, то и второй имеет такую же величину. Следовательно, треугольник равнобедренный, его катеты имеют одинаковую длину, а их соотношение в любом случае будет равно 1.
Заключение
Тригонометрия — сложная наука, которая не находит практически никакого применения в повседневной жизни. Однако без тригонометрии не было бы современных технологий, поэтому специалистам прикладных наук без нее никуда. Используйте наши онлайн-калькуляторы для расчета значений тригонометрических функций.
Что такое тангенс угла и как его найти
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
» alt=»»>
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
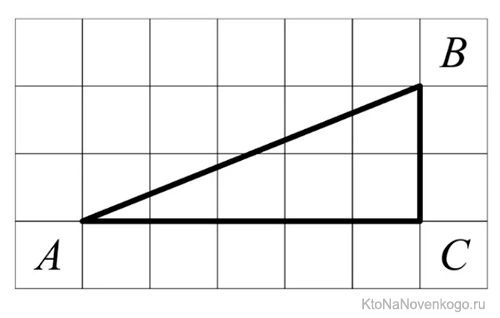
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Я Очень Люблю Правила, Теоремы, Формулы по Предмету «Математика», «Алгебра».
Прочитал статью и остался один главный вопрос, а собственно без вспомогательных таблиц найти угол В ГРАДУСАХ вообще возможно и есть ли у вас статья, где рассказыввается как это сделать? Спасибо.
Я ни разу не математик, но почему у вас сумма углов прямоугольного треугольника равна 90 градусов. А так все хорошо начиналось. Объясняете хорошо, но после таких ошибок у меня сомнения что информация верная.
Спасибо. Уточнил в тексте, что это сумма двух непрямых углов прямоугольного треугольника.
Пишу стихи. Востребован тангенс для решения жизненных ситуаций поскольку состоит из тех же функций,как-то, касающийся,прилежащий, трогающий. Куда без них денешься.
Таблица ТАНГЕНСОВ для углов от 0° до 360° градусов
ТАНГЕНС (Tg α) острого угла в прямоугольном треугольнике равняется отношение противолежащего катета к прилежащему катету.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tg α (Тангенс) | 0 | 1/√3 | 1 | √3 | — | 0 | — | 0 |
| Угол в градусах | tg (Тангенс) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0524 |
| 4° | 0.0699 |
| 5° | 0.0875 |
| 6° | 0.1051 |
| 7° | 0.1228 |
| 8° | 0.1405 |
| 9° | 0.1584 |
| 10° | 0.1763 |
| 11° | 0.1944 |
| 12° | 0.2126 |
| 13° | 0.2309 |
| 14° | 0.2493 |
| 15° | 0.2679 |
| 16° | 0.2867 |
| 17° | 0.3057 |
| 18° | 0.3249 |
| 19° | 0.3443 |
| 20° | 0.364 |
| 21° | 0.3839 |
| 22° | 0.404 |
| 23° | 0.4245 |
| 24° | 0.4452 |
| 25° | 0.4663 |
| 26° | 0.4877 |
| 27° | 0.5095 |
| 28° | 0.5317 |
| 29° | 0.5543 |
| 30° | 0.5774 |
| 31° | 0.6009 |
| 32° | 0.6249 |
| 33° | 0.6494 |
| 34° | 0.6745 |
| 35° | 0.7002 |
| 36° | 0.7265 |
| 37° | 0.7536 |
| 38° | 0.7813 |
| 39° | 0.8098 |
| 40° | 0.8391 |
| 41° | 0.8693 |
| 42° | 0.9004 |
| 43° | 0.9325 |
| 44° | 0.9657 |
| 45° | 1 |
| 46° | 1.0355 |
| 47° | 1.0724 |
| 48° | 1.1106 |
| 49° | 1.1504 |
| 50° | 1.1918 |
| 51° | 1.2349 |
| 52° | 1.2799 |
| 53° | 1.327 |
| 54° | 1.3764 |
| 55° | 1.4281 |
| 56° | 1.4826 |
| 57° | 1.5399 |
| 58° | 1.6003 |
| 59° | 1.6643 |
| 60° | 1.7321 |
| 61° | 1.804 |
| 62° | 1.8807 |
| 63° | 1.9626 |
| 64° | 2.0503 |
| 65° | 2.1445 |
| 66° | 2.246 |
| 67° | 2.3559 |
| 68° | 2.4751 |
| 69° | 2.6051 |
| 70° | 2.7475 |
| 71° | 2.9042 |
| 72° | 3.0777 |
| 73° | 3.2709 |
| 74° | 3.4874 |
| 75° | 3.7321 |
| 76° | 4.0108 |
| 77° | 4.3315 |
| 78° | 4.7046 |
| 79° | 5.1446 |
| 80° | 5.6713 |
| 81° | 6.3138 |
| 82° | 7.1154 |
| 83° | 8.1443 |
| 84° | 9.5144 |
| 85° | 11.4301 |
| 86° | 14.3007 |
| 87° | 19.0811 |
| 88° | 28.6363 |
| 89° | 57.29 |
| 90° | ∞ |
| Угол | tg (Тангенс) |
|---|---|
| 91° | -57.29 |
| 92° | -28.6363 |
| 93° | -19.0811 |
| 94° | -14.3007 |
| 95° | -11.4301 |
| 96° | -9.5144 |
| 97° | -8.1443 |
| 98° | -7.1154 |
| 99° | -6.3138 |
| 100° | -5.6713 |
| 101° | -5.1446 |
| 102° | -4.7046 |
| 103° | -4.3315 |
| 104° | -4.0108 |
| 105° | -3.7321 |
| 106° | -3.4874 |
| 107° | -3.2709 |
| 108° | -3.0777 |
| 109° | -2.9042 |
| 110° | -2.7475 |
| 111° | -2.6051 |
| 112° | -2.4751 |
| 113° | -2.3559 |
| 114° | -2.246 |
| 115° | -2.1445 |
| 116° | -2.0503 |
| 117° | -1.9626 |
| 118° | -1.8807 |
| 119° | -1.804 |
| 120° | -1.7321 |
| 121° | -1.6643 |
| 122° | -1.6003 |
| 123° | -1.5399 |
| 124° | -1.4826 |
| 125° | -1.4281 |
| 126° | -1.3764 |
| 127° | -1.327 |
| 128° | -1.2799 |
| 129° | -1.2349 |
| 130° | -1.1918 |
| 131° | -1.1504 |
| 132° | -1.1106 |
| 133° | -1.0724 |
| 134° | -1.0355 |
| 135° | -1 |
| 136° | -0.9657 |
| 137° | -0.9325 |
| 138° | -0.9004 |
| 139° | -0.8693 |
| 140° | -0.8391 |
| 141° | -0.8098 |
| 142° | -0.7813 |
| 143° | -0.7536 |
| 144° | -0.7265 |
| 145° | -0.7002 |
| 146° | -0.6745 |
| 147° | -0.6494 |
| 148° | -0.6249 |
| 149° | -0.6009 |
| 150° | -0.5774 |
| 151° | -0.5543 |
| 152° | -0.5317 |
| 153° | -0.5095 |
| 154° | -0.4877 |
| 155° | -0.4663 |
| 156° | -0.4452 |
| 157° | -0.4245 |
| 158° | -0.404 |
| 159° | -0.3839 |
| 160° | -0.364 |
| 161° | -0.3443 |
| 162° | -0.3249 |
| 163° | -0.3057 |
| 164° | -0.2867 |
| 165° | -0.2679 |
| 166° | -0.2493 |
| 167° | -0.2309 |
| 168° | -0.2126 |
| 169° | -0.1944 |
| 170° | -0.1763 |
| 171° | -0.1584 |
| 172° | -0.1405 |
| 173° | -0.1228 |
| 174° | -0.1051 |
| 175° | -0.0875 |
| 176° | -0.0699 |
| 177° | -0.0524 |
| 178° | -0.0349 |
| 179° | -0.0175 |
| 180° | 0 |
| Угол | tg (Тангенс) |
|---|---|
| 181° | 0.0175 |
| 182° | 0.0349 |
| 183° | 0.0524 |
| 184° | 0.0699 |
| 185° | 0.0875 |
| 186° | 0.1051 |
| 187° | 0.1228 |
| 188° | 0.1405 |
| 189° | 0.1584 |
| 190° | 0.1763 |
| 191° | 0.1944 |
| 192° | 0.2126 |
| 193° | 0.2309 |
| 194° | 0.2493 |
| 195° | 0.2679 |
| 196° | 0.2867 |
| 197° | 0.3057 |
| 198° | 0.3249 |
| 199° | 0.3443 |
| 200° | 0.364 |
| 201° | 0.3839 |
| 202° | 0.404 |
| 203° | 0.4245 |
| 204° | 0.4452 |
| 205° | 0.4663 |
| 206° | 0.4877 |
| 207° | 0.5095 |
| 208° | 0.5317 |
| 209° | 0.5543 |
| 210° | 0.5774 |
| 211° | 0.6009 |
| 212° | 0.6249 |
| 213° | 0.6494 |
| 214° | 0.6745 |
| 215° | 0.7002 |
| 216° | 0.7265 |
| 217° | 0.7536 |
| 218° | 0.7813 |
| 219° | 0.8098 |
| 220° | 0.8391 |
| 221° | 0.8693 |
| 222° | 0.9004 |
| 223° | 0.9325 |
| 224° | 0.9657 |
| 225° | 1 |
| 226° | 1.0355 |
| 227° | 1.0724 |
| 228° | 1.1106 |
| 229° | 1.1504 |
| 230° | 1.1918 |
| 231° | 1.2349 |
| 232° | 1.2799 |
| 233° | 1.327 |
| 234° | 1.3764 |
| 235° | 1.4281 |
| 236° | 1.4826 |
| 237° | 1.5399 |
| 238° | 1.6003 |
| 239° | 1.6643 |
| 240° | 1.7321 |
| 241° | 1.804 |
| 242° | 1.8807 |
| 243° | 1.9626 |
| 244° | 2.0503 |
| 245° | 2.1445 |
| 246° | 2.246 |
| 247° | 2.3559 |
| 248° | 2.4751 |
| 249° | 2.6051 |
| 250° | 2.7475 |
| 251° | 2.9042 |
| 252° | 3.0777 |
| 253° | 3.2709 |
| 254° | 3.4874 |
| 255° | 3.7321 |
| 256° | 4.0108 |
| 257° | 4.3315 |
| 258° | 4.7046 |
| 259° | 5.1446 |
| 260° | 5.6713 |
| 261° | 6.3138 |
| 262° | 7.1154 |
| 263° | 8.1443 |
| 264° | 9.5144 |
| 265° | 11.4301 |
| 266° | 14.3007 |
| 267° | 19.0811 |
| 268° | 28.6363 |
| 269° | 57.29 |
| 270° | ∞ |
| Угол | tg (Тангенс) |
|---|---|
| 271° | -57.29 |
| 272° | -28.6363 |
| 273° | -19.0811 |
| 274° | -14.3007 |
| 275° | -11.4301 |
| 276° | -9.5144 |
| 277° | -8.1443 |
| 278° | -7.1154 |
| 279° | -6.3138 |
| 280° | -5.6713 |
| 281° | -5.1446 |
| 282° | -4.7046 |
| 283° | -4.3315 |
| 284° | -4.0108 |
| 285° | -3.7321 |
| 286° | -3.4874 |
| 287° | -3.2709 |
| 288° | -3.0777 |
| 289° | -2.9042 |
| 290° | -2.7475 |
| 291° | -2.6051 |
| 292° | -2.4751 |
| 293° | -2.3559 |
| 294° | -2.246 |
| 295° | -2.1445 |
| 296° | -2.0503 |
| 297° | -1.9626 |
| 298° | -1.8807 |
| 299° | -1.804 |
| 300° | -1.7321 |
| 301° | -1.6643 |
| 302° | -1.6003 |
| 303° | -1.5399 |
| 304° | -1.4826 |
| 305° | -1.4281 |
| 306° | -1.3764 |
| 307° | -1.327 |
| 308° | -1.2799 |
| 309° | -1.2349 |
| 310° | -1.1918 |
| 311° | -1.1504 |
| 312° | -1.1106 |
| 313° | -1.0724 |
| 314° | -1.0355 |
| 315° | -1 |
| 316° | -0.9657 |
| 317° | -0.9325 |
| 318° | -0.9004 |
| 319° | -0.8693 |
| 320° | -0.8391 |
| 321° | -0.8098 |
| 322° | -0.7813 |
| 323° | -0.7536 |
| 324° | -0.7265 |
| 325° | -0.7002 |
| 326° | -0.6745 |
| 327° | -0.6494 |
| 328° | -0.6249 |
| 329° | -0.6009 |
| 330° | -0.5774 |
| 331° | -0.5543 |
| 332° | -0.5317 |
| 333° | -0.5095 |
| 334° | -0.4877 |
| 335° | -0.4663 |
| 336° | -0.4452 |
| 337° | -0.4245 |
| 338° | -0.404 |
| 339° | -0.3839 |
| 340° | -0.364 |
| 341° | -0.3443 |
| 342° | -0.3249 |
| 343° | -0.3057 |
| 344° | -0.2867 |
| 345° | -0.2679 |
| 346° | -0.2493 |
| 347° | -0.2309 |
| 348° | -0.2126 |
| 349° | -0.1944 |
| 350° | -0.1763 |
| 351° | -0.1584 |
| 352° | -0.1405 |
| 353° | -0.1228 |
| 354° | -0.1051 |
| 355° | -0.0875 |
| 356° | -0.0699 |
| 357° | -0.0524 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Чему равен тангенс 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.5774