Как посчитать сумму в маткаде

Как посчитать сумму в маткаде

3.2.2. Вычислительные операторы

Вычислительные операторы вставляются в документы при помощи панели инструментов Calculus (Вычисления). При нажатии любой из кнопок в документе появляется символ соответствующего математического действия, снабженный несколькими местозаполнителями. Количество и расположение местозаполнителей определяется типом оператора и в точности соответствует их общепринятой математической записи. Например, при вставке оператора суммы (рис. 3.7) необходимо задать четыре величины: переменную, по которой надо произвести суммирование, нижний и верхний пределы, а также само выражение, которое будет стоять под знаком суммы (пример заполненного оператора суммы см. ниже в листинге 3.22).

Для того чтобы вычислить неопределенный интеграл, следует заполнить два местозаполнителя: подынтегрального выражения и переменной интегрирования.

Рис. 3.7. Вставка оператора суммирования

Перечислим основные вычислительные операторы и приведем простейшие примеры их применения:

Листинг 3.20. Операторы вычисления производных

Листинг 3.21. Операторы интегрирования

Листинг 3.22. Операторы суммирования и вычисления произведения

Листинг 3.23. Операторы суммировани и вычисления произведения

О назначении и особенностях использования ранжированных переменных будет рассказано в следующей главе (см. разд. «Ранжированные переменные» гл. 4).

Листинг З.24. Операторы символьного вычисления пределов

В отличие от других, операторы поиска предела могут быть вычислены только символьно (см. гл. 5).

Операторы суммирования и вычисления произведения фактически являются более удобной записью операторов + и х с большим количеством операндов. А вот вычислительные операторы поиска производных и интегралов существенно отличаются от операторов умножения и сложения тем, что реализованы на основе определенных численных методов, которые в скрытой (невидимой для пользователя) форме запускаются вычислительным процессором Mathcad. При численном расчете интегралов и производных необходимо, хотя бы в общих чертах, представлять принцип работы соответствующих алгоритмов, чтобы избежать ошибок и неожиданностей при получении результатов (численным методам интегрирования и дифференцирования посвящена гл. 7).

Рис. 3.8. Поиск бесконечного ряда

Важно отметить, что имеется возможность вычислять интегралы с одним или обоими бесконечными пределами, а также в символьной форме искать значения бесконечных пределов, сумм (рядов) и произведений. Для удобства ввода кнопка с символом бесконечности помещена на ту же панель инструментов Calculus (Вычисления). Пример вставки символа бесконечности в задаче поиска бесконечного ряда приведен на рис. 3.8.

Источник

Сумма элементов строки матрицы

Сумма элементов строки матрицы
Никак не могу понять, как просуммировать строку для каждого столбца. Вот как на примере.

Сумма элементов строки i и столбца j случайной матрицы n x m
Требуется найти сумму элементов строки i и столбца j случайной матрицы n x m Матрицу сделал, а.

Сумма элементов матрицы
Помогите решить задачу в матлабе. Дана целочисленная квадратичная матрица порядка 5.Найти сумму ее.

Сумма элементов матрицы.
Нужно сложить в матрице все неотрицательные элементы ниже главной диагонали и сколько элементов.

Сумма элементов главной диагонали матрицы D
Как сделать поэлементно, не применяя функцию? Размерность 3 А какую функцию Вы собирались тут.

Сумма соседних элементов матрицы вектора
Здравствуйте форумчане, прошу у вас помощи. Есть массив матрица-вектор (1 столбец и 8147 строк).

Сумма элементов главной диагонали матрицы
В общем задание состоит в нахождении суммы элементов главной диагонали матрицы. Объясните.

Сумма элементов второй строки массива
Дана матрица из трех строк. Первая строка состоит из элементов 2, 3, 1, 4, 6, 5. Вторая строка.

Сумма элементов строки в матрице и нахождение максимальной
Нужно найти максимальную сумму элементов в строке. И расположить строки в порядке возрастания.

Источник

Как посчитать сумму в маткаде

БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ

1 Запуск. Формульные и текстовые области

Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).

Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:

Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!

Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.

2 Ранжированные переменные. Функции. Графики

В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.

Ранжированная переменная общего вида определяется выражением:

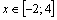
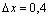
Например, если переменная изменяется в интервале с шагом , то она задается в виде

Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.

Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку панели инструментов. При этом появляется окно, где справа перечислены возможные категории функций, а слева – список функций из выделенной категории.

Среди наиболее часто используемых функций можно указать:

Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется

Имя(список аргументов) := Выражение

Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.

Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.

Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).

Для построения графика функции одной переменной в декартовой системе координат в Mathcad:

Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

– вектор-столбец; – вектор-строка.

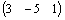
Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:

Существует несколько способов создания массивов.

1-й способ. Использование панели Matrix (Матрицы).

Сначала набирается имя массива и оператор присваивания, например, 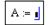. Далее на панели Math (Математика) выбираем кнопку Matrix (Матриц):

Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.

На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:

2-й способ. Использование ранжированной переменной.

Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:

Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма 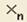с палитры математических инструментов Matrix. Для элемента матрицы указываются через запятую два индекса, обозначающих номер строки и номер столбца соответственно.

Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.

Таблица 1 – Команды палитры инструментов Matrix (Матрица)

Источник

Найти сумму максимальных элементов строк в двухмерном массиве (через программирования)

. Помогите, кому не сложно и кто разбирается.

Т.е в моем примере должна произвестись сумма 3+5+3. Каждое значение максимально в каждой из 3х строк соответственно.

Массив: В двухмерном массиве найти сумму нечетных элементов четных строк.
В двухмерном массиве найти сумму нечетных элементов четных строк

В двумерном массиве произвольной размерности найти сумму максимальных элементов строк
Помогите решить, пожалуйста. В двумерном массиве произвольной размерности найти сумму.

В двухмерном массиве вычислить сумму отрицательных элементов всех нечетных строк
Помогите плиз сделать прогу. 1. Ввести двухмерный массив поэлементно с помощью клавиатуры или.

В двухмерном массиве целых чисел посчитать сумму элементов строк, столбцов, общую
1. В двухмерном массиве целых чисел, заполненном случайным образом целыми числами в диапазоне от –.

и архив с файлом mathcad 4.rar

Вот, теперь тут точно все как на скриншоте, ошибка пропала, но ответ странный какой-то.Явно не тот, как программа должна работать

Решение

Найти в двухмерном массиве номера строк с наибольшей суммой элементов
1)Напишите программу, находящую в двухмерном массиве номера строк с наибольшей суммой элементов.

В двухмерном массиве 3х4, найти сумму элементов 2-ой строки
1. Одномерные массивы. 2.Оператор выбора CASE. 3.В двухмерном массиве 3х4, найти сумму элементов.

Найти сумму элементов в каждом столбце в двухмерном массиве
Пожалуйста,помогите написать программы.1)Найти сумму элементов в каждом столбце,в двухмерном.

В двухмерном массиве найти сумму отрицательных элементов пятой строки
А)Сумму отрицательных элементов пятой строки Б)Сумму элементов пятой строки массива, меньших 100.

В двухмерном целочисленном массиве 20х10 найти сумму элементов по диагонали
В двухмерном целочисленном массиве 20х10 найти сумму элементов по диагонали

В массиве найти сумму минимальных элементов в строках и сумму максимальных элементов в столбцах
Помогите написать программу, простую, чтобы была понятна. В двумерном целочисленном массиве.

Источник

Как посчитать сумму в маткаде

Совет
Никогда не применяйте для обозначения скалярного произведения символ х,который является общеупотребительным символом векторного произведения (см. разд. 9.1.7).

Рис. 9.3. Оператор векторизации
Листинг 9.16. Использование векторизациидля перемножения элементов вектора

Оператор векторизации можно использовать только с векторами и матрицами одинакового размера.
Большинство неспецифических функций MathCAD не требуют векторизации для проведения одной и той же операции над всеми элементами вектора. Например, аргументом тригонометрических функций по определениюявляется скаляр. Если попытаться вычислить синус векторной величины,MathCAD осуществит векторизацию по умолчанию, вычислив синус каждого элемента и выдав в качестве результата соответствующий вектор. Пример показан в листинге 9.17.
Листинг 9.17. Векторизация необязательнадля большинства функций MathCAD

9.1.12. Символьные операции с матрицами
Все матричные и векторные операторы, о которых шла речь выше, допустимо использовать в символьных вычислениях. Мощь символьных операцийзаключается в возможности проводить их не только над конкретными числами, но и над переменными. Несколько примеров приведены в листинге 9.18.
Листинг 9.18. Примеры символьных операций над векторами и матрицами

Cовет
Смело используйте символьный процессор в качестве мощного математического справочника. Например, когда вы хотите вспомнить какое-либо определение из области линейной алгебры (так, правила перемножения и обращенияматриц показаны в первых строках листинга 9.18).

Примечание
О вложенных массивах читайте в разд. «Создание тензора» гл. 4.

Пример использования функции CreateSpace показан на рис. 9.4. Заметьте, дляпостроения графика спирали не потребовалось никакого дополнительногокода, кроме определения параметрической зависимости в вектор-функции F!

Примечание
Размер NXM матрицы А для функции geninv должен быть таким, чтобы N>M.

Примечание
Выделить из матрицы один столбец или строку можно и с помощью функции submatrix.

Примечание
Число элементов вектора и индекс его последнего элемента совпадают, еслииндексы нумеруются с 1, т. е. системная константа ORIGIN равна 1 (см. гл. 4).

Примечание
Если элементы матриц или векторов комплексные, то сортировка ведется подействительной части, а мнимая часть игнорируется.

Совет
В большинстве задач неважно, какую норму использовать. Как видно, в обычных случаях разные нормы дают примерно одинаковые значения, хорошо отражая порядок величины матричных элементов. Определение остальных нормзаинтересованный читатель отыщет в справочниках по линейной алгебре илив Центре Ресурсов MathCAD.

Примечание
Как нетрудно понять, матрицы А и в из предыдущего листинга 9.30 обладаютодинаковыми числами обусловленности, т.к. в=100-А, и, следовательно, обематрицы определяют одну и ту же систему уравнений.

Примечание
К системам линейных уравнений сводится множество, если не сказать большинство, задач вычислительной математики. Один из таких примеров приведен в разд. «Разностные схемы»гл. 12.

Примечание
Соответствующая матрице А и вектору B система уравнений выписана явнов листинге 9.35.

Листинг 9.33. Решение СЛАУ

Листинг 9.34. Символьное решение СЛАУ (продолжение листинга 9.33)

В некоторых случаях, для большей наглядности представления СЛАУ, егоможно решить точно так же, как систему нелинейных уравнений (см. гл. 8). Пример численного решения СЛАУ из предыдущих листингов показан влистинге 9.35. Не забывайте, что при численном решении всем неизвестнымтребуется присвоить начальные значения (это сделано в первой строке листинга 9.35). Они могут быть произвольными, т. к. решение СЛАУ с невырожденной матрицей единственно.

Примечание
Фактически, треугольное разложение матрицы системы линейных уравненийпроизводится при ее решении численным методом Гаусса.

Источник