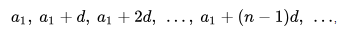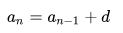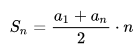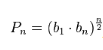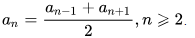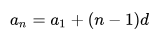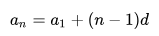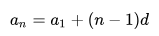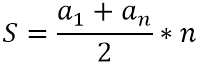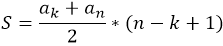Как посчитать сумму математической прогрессии

Как посчитать сумму математической прогрессии

Сначала разберёмся со смыслом и формулой суммы. А потом и порешаем. В своё удовольствие.) Смысл суммы прост, как мычание. Чтобы найти сумму арифметической прогрессии надо просто аккуратно сложить все её члены. Если этих членов мало, можно складывать безо всяких формул. Но если много, или очень много. сложение напрягает.) В этом случае спасает формула.

Формула суммы выглядит просто:

Разберёмся, что за буковки входят в формулу. Это многое прояснит.

a₁ — первый член прогрессии. Здесь всё понятно, это просто первое число ряда.

Определимся с понятием последнего члена a_n. Вопрос на засыпку: какой член будет последним, если дана бесконечная арифметическая прогрессия?)

Для уверенного ответа нужно понимать элементарный смысл арифметической прогрессии и. внимательно читать задание!)

В задании на поиск суммы арифметической прогрессии всегда фигурирует (прямо или косвенно) последний член, которым следует ограничиться. Иначе конечной, конкретной суммы просто не существует. Для решения не суть важно, какая задана прогрессия: конечная, или бесконечная. Не суть важно, как она задана: рядом чисел, или формулой n-го члена.

Примеры заданий на сумму арифметической прогрессии.

Прежде всего, полезная информация:

Основная сложность в заданиях на сумму арифметической прогрессии заключается в правильном определении элементов формулы.

1. Арифметическая прогрессия задана условием: a_n = 2n-3,5. Найдите сумму первых 10 её членов.

Хорошее задание. Лёгкое.) Нам для определения суммы по формуле чего надо знать? Первый член a₁, последний член a_n, да номер последнего члена n.

Мы выяснили значение всех элементов формулы суммы арифметической прогрессии. Остаётся подставить их, да посчитать:

Вот и все дела. Ответ: 75.

Ещё задание на основе ГИА. Чуть посложнее:

2. Дана арифметическая прогрессия (a_n), разность которой равна 3,7; a₁=2,3. Найти сумму первых 15 её членов.

Сразу пишем формулу суммы:

Смотрим, что у нас для формулы есть, а чего не хватает. Есть первый член и количество членов:

Эта формулка позволяет нам найти значение любого члена по его номеру. Ищем простой подстановкой:

Осталось подставить все элементы в формулу суммы арифметической прогрессии и посчитать ответ:

Кстати, если в формулу суммы вместо a_n просто подставим формулу n-го члена, получим:

Приведём подобные, получим новую формулу суммы членов арифметической прогрессии:

Как видим, тут не требуется n-й член a_n. В некоторых задачах эта формула здорово выручает, да. Можно эту формулу запомнить. А можно в нужный момент её просто вывести, как здесь. Ведь формулу суммы и формулу n-го члена всяко надо помнить.)

Теперь задание в виде краткой шифровки):

3. Найти сумму всех положительных двузначных чисел, кратных трём.

Во как! Ни тебе первого члена, ни последнего, ни прогрессии вообще. Как жить!?

Кратные трём. Гм. Это такие числа, которые делятся на три нацело, вот! Десятка не делится на три, 11 не делится. 12. делится! Так, кое-что вырисовывается. Уже можно записать ряд по условию задачи:

Будет ли этот ряд арифметической прогрессией? Конечно! Каждый член отличается от предыдущего строго на тройку. Если к члену прибавить 2, или 4, скажем, результат, т.е. новое число, уже не поделится нацело на 3. До кучи можно сразу и разность арифметической прогрессии определить: d = 3. Пригодится!)

Итак, можно смело записать кое-какие параметры прогрессии:

Смотрим на формулу суммы арифметической прогрессии:

Смотрим, и радуемся.) Мы вытащили из условия задачи всё необходимое для расчёта суммы:

Остаётся элементарная арифметика. Подставляем числа в формулу и считаем:

Ещё один тип популярных задачек:

4. Дана арифметическая прогрессия:

Найти сумму членов с двадцатого по тридцать четвёртый.

Смотрим на формулу суммы и. огорчаемся.) Формула, напомню, считает сумму с первого члена. А в задаче нужно считать сумму с двадцатого. Не сработает формула.

Можно, конечно, расписать всю прогрессию в ряд, да поскладывать члены с 20 по 34. Но. как-то тупо и долго получается, правда?)

Отсюда видно, что найти сумму S_20-34 можно простым вычитанием

Обе суммы в правой части считаются с первого члена, т.е. к ним вполне применима стандартная формула суммы. Приступаем?

Вытаскиваем из условия задачи парметры прогрессии:

Для расчёта сумм первых 19 и первых 34 членов нам нужны будут 19-й и 34-й члены. Считаем их по формуле n-го члена, как в задаче 2:

Остаётся всего ничего. От суммы 34 членов отнять сумму 19 членов:

В этом уроке мы рассмотрели задачи, для решения которых достаточно понимать смысл суммы арифметической прогрессии. Ну и пару формул знать надо.)

При решении любой задачи на сумму арифметической прогрессии рекомендую сразу выписывать две главные формулы из этой темы.

Формулу суммы n первых членов арифметической прогрессии:

Эти формулы сразу подскажут, что нужно искать, в каком направлении думать, чтобы решить задачу. Помогает.

А теперь задачи для самостоятельного решения.

5. Найти сумму всех двузначных чисел, которые не делятся нацело на три.

Круто?) Подсказка скрыта в замечании к задаче 4. Ну и задачка 3 поможет.

6. Арифметическая прогрессия задана условием: a₁ =-5,5; a_n+1= a_n+0,5. Найдите сумму первых 24 её членов.

Непривычно?) Это рекуррентная формула. Про неё можно прочитать в предыдущем уроке. Не игнорируйте ссылку, такие задачки в ГИА частенько встречаются.

7. Вася накопил к Празднику денег. Целых 4550 рублей! И решил подарить самому любимому человеку (себе) несколько дней счастья). Пожить красиво, ни в чём себе не отказывая. Потратить в первый день 500 рублей, а в каждый последующий день тратить на 50 рублей больше, чем в предыдущий! Пока не кончится запас денег. Сколько дней счастья получилось у Васи?

Сложно?) Поможет дополнительная формула из задачи 2.

Источник

Арифметическая (алгебраическая) прогрессия определение, примеры нахождения с решением

Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.

Одна из главных отличительных особенностей такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.

Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.

Онлайн-калькулятор арифметической прогрессии

Определение и примеры арифметической прогрессии

Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.

Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.

Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.

Кроме этого, существуют виды таких рядов:

В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.

Виды арифметической (алгебраической) прогрессии

Разновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля.

Таким образом, можно встретить определенные вариации:

Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является.

Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель.

Формулы арифметической прогрессии

Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.

Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d):

Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.

Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:

Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы.

Произведение членов арифметической прогрессии можно находить по похожей формуле:

где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов.

Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:

Примеры задач с решением

Рассмотрим как решать задачи на заданную тему.

Пример 1

Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».

Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – и получаем d = 7. Теперь мы можем считать по формуле:

Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7.

После вычисления получаем ответ: a574 = 4019.

Пример 2

Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.

Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:

Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8.

Вычисляя, получаем ответ а544 = 4361.

Пример 3

Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.

Требуется выяснить, сколько времени у студента ушло на подготовку.

Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:

После подстановки получаем выражение: 730 = 17 + (n 1) * 27.

После вычислений определяем ответ – 27 дней.

Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.

Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Сумма арифметической прогрессии.
Дано: a₁, d, n
Найти: S_n

Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа \( a_1 \) и \( d \) можно задать не только целые, но и дробные.
Число \( n \) может быть только целым положительным.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так 2.5 или так 2,5

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

Введите числа a₁, d, n Найти сумму S_n

Немного теории.

Числовая последовательность

В повседневной практике часто используется нумерация различных предметов, чтобы указать порядок их расположения. Например, дома на каждой улице нумеруются. В библиотеке нумеруются читательские абонементы и затем располагаются в порядке присвоенных номеров в специальных картотеках.

Арифметическая прогрессия

Продолжительность года приблизительно равна 365 суткам. Более точное значение равно \( 365\frac<1> <4>\) суток, поэтому каждые четыре года накапливается погрешность, равная одним суткам.

Для учёта этой погрешности к каждому четвёртому году добавляются сутки, и удлинённый год называют високосным.

В этой последовательности каждый её член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом 4. Такие последовательности называют арифметическими прогрессиями.

По определению арифметической прогрессии имеем:
\( a_=a_n+d, \quad a_=a_n-d, \)
откуда
\( a_n= \frac +a_> <2>\), где \( n>1 \)

Таким образом, каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Этим объясняется название «арифметическая» прогрессия.

Отметим, что если a₁ и d заданы, то остальные члены арифметической прогрессии можно вычислить по рекуррентной формуле a_n+1 = a_n + d. Таким способом нетрудно вычислить несколько первых членов прогрессии, однако, например, для a₁₀₀ уже потребуется много вычислений. Обычно для этого используется формула n-го члена. По определению арифметической прогрессии
\( a_2=a_1+d, \)
\( a_3=a_2+d=a_1+2d, \)
\( a_4=a_3+d=a_1+3d \)
и т.д.
Вообще,
\( a_n=a_1+(n-1)d, \)
так как n-й член арифметической прогрессии получается из первого члена прибавлением (n-1) раз числа d.
Эту формулу называют формулой n-го члена арифметической прогрессии.

Сумма n первых членов арифметической прогрессии

Так как \( a_n=a_1+(n-1)d \), то заменив в этой формуле a_n получим еще одну формулу для нахождения суммы n первых членов арифметической прогрессии:
$$ S_n = n \cdot \frac<2a_1+(n-1)d> <2>$$

Источник

Сумма арифметической прогрессии

Бытует мнение, что формула суммы арифметической прогрессии была открыта еще Гауссом, как быстрый и точный способ расчета суммы чисел в определенной последовательности. Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда.

Соответственно, он нашел данную сумму и умножил ее на половину от общего количества чисел в последовательности, участвующих в расчете суммы. Таким образом, была выведена формула суммы арифметической прогрессии

Пример. Предположим, задано условие: «Найдите сумму первых десяти (10) членов арифметической прогрессии». Для этого понадобится следующие данные: разность прогрессии и первый ее член. Если в задаче дан какой-либо n член арифметической прогрессии вместо первого, тогда сначала нужно воспользоваться разделом, где представлена формула нахождения первого члена прогрессии, и найти его. Затем исходные данные вбиваются в калькулятор и он производит расчеты, складывая первый и десятый члены, и умножая полученную сумму на половину от общего количества складываемых членов – на 5. Аналогично происходит, если нужно найти сумму первых шести членов или любого другого количества.

В случае, когда необходимо найти сумму членов арифметической прогрессии, начинающихся не с первого, а с пятого члена, к примеру, тогда среднее арифметическое остается тем же, а общее количество членов берется как увеличенная на единицу разность между порядковыми номерами взятых членов.

Источник

Арифметическая прогрессия онлайн

С помощю этого онлайн калькулятора можно найти сумму первых n членов арифметической прогрессии при разных начальных данных. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Арифметической прогрессией называется числовая последовательность, каждый член которого, начиная со второго равен сумме предыдующего числа и некоторого постоянного числа d.

d— называется разностью прогрессии.

Очевидно, что при d >0 арифметическая прогрессия является возрастающей прогрессией, а при d Свойство 1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдующего и последующего членов.

Доказательство. Из определения арифметической прогрессии, имеем:

Свойство 2 (обратное). Если в последовательности каждый член, начиная со второго, является средним арифметическим предыдующего и последующего членов, то эта последовательность является арифметической прогрессией.

Из равенства (4) видно, что разность между предыдующими и последующими членами последовательности остаются постоянной. А это значит, что последовательность является арифметической прогрессией.

Из свойств 1 и 2 можно сформулировать необходимое и достаточное для того,чтобы последовательность являлся арифметической прогрессией.

Свойство 3. Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго есть средее арифметическое предыдующего и последующего членов.

Свойство 3 называется характеристическим свойством арифметической прогрессии.

Пример 1. Известно, что арифметическая прогрессия, разность которой равна d. Определить, является ли арифметической прогрессией последовательность ниже, и если да, то определить ее разность:

Легко заметить, что предыдующый и последующий члены последовательности (5), начиная с − это и , соответственно.

Учитывая, что арифметическая прогрессия, можем записать:

Из равенства (8) и свойства 3 следует, что последовательность (5) является арифметической прогрессией, а из (6) и (7) следует, что разность арифметической прогрессии равно 2d.

Пример 2. Известно, что арифметическая прогрессия, разность которой равна d. Определить, является ли арифметической прогрессией последовательность

и если да, то определить ее разность.

Решение. Запишем последовательность (9) в следующем виде:

,

,

(10)

.

(11)

Поскольку арифметическая прогрессия, то

Из выражений (10)-(12) следует:

Следовательно последовательность (9) является арифметической прогрессией. Далее определим разность арифметической прогрессии (9). Так как разность арифметической прогрессии равна d, то имеем

Из (10), (11) и (13) следует, что разность арифметической прогрессии (9) равна −d.

Пример 3. Найти все члены арифметической прогрессии, обозначенные буквами

.

(14)

Подставляя значения и в последнее равенство, получим

Вычисляем все члены арифметической прогрессии, обозначенные буквами

Сумма первых n членов арифметической прогрессии

В этом параграфе мы выведем формулу суммы первых n членов арифметической прогрессии. Для этого докажем, сначала следующее свойство арифметической прогресии:

Свойство 4. Пусть арифметическая прогрессия и пусть натуральные числа и . Тогда .

Доказательство. Пусть d разность прогрессии, тогда

,

.

получим .

Из доказанного свойства следует, что в конечной арифметической прогресии сумма крайных членов равно сумме членов, равноудаленных от крайных членов.

Действительно. Пусть p и q первый и последний члены конечной арифметической прогрессии и пусть . Тогда . Перепишем равенство (15) так:

Откуда следует, что в конечной арифметической прогресии сумма крайных членов равно сумме членов, равноудаленных от крайных членов (Рис.2).

Теперь выведем формулу суммы первых n членов арифметической прогрессии. Обозначим через S_n сумму первых n членов арифметической прогрессии . Запишем два равенства располагая в первом случае все члены арифметической прогрессии в порядке возрастания, а во втором случае в порядке убывания номеров:

Складывая эти равенства, получим

Из свойства 4 следует, что

Формулу (16) можно записать и в другом виде учитывая, что

Рассмотрим примеры применения формулы суммы первых n членов арифметической прогрессии.

Решение. Запишем формулы 3-го и 14-го членов арифметической прогрессии используя формулу (2):

Сложив эти уравнения, получим:

Запишем далее формулу суммы первых 16 членов арифметической прогресии используя формулу (17):

Далее, из (18) и (19) получим:

Пример 5. Известно, что (x_n) арифметическая прогрессия, в которой x₁=7, x₂₅=63. Найти x₁₃ и сумму членов с тринадцатого до двадцать пятый включительно.

Решение. Запишем фомулу для двадцать пятого члена арифметической прогрессии используя формулу (2):

Подставим значения в (20):

Далее, найдем тринадцатый член арифметической прогресии:

.

Найдем суммы первых двенадцати и первых двадцати пяти членов арифметической прогрессии:

Сумма членов арифметической прогрессии с тринадцатого до двадцать пятый включительно равна:

Источник