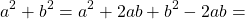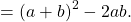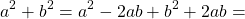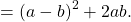Как посчитать сумму квадратов чисел
Сумма квадратов всех целых чисел
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b) 2 = a 2 ± 2ab + b 2
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a 2 + b 2 = (a + b) 2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Как посчитать сумму квадратов в Excel
Нахождение суммы квадратов в Microsoft Excel может быть повторяющейся задачей. Наиболее очевидная формула требует ввода большого количества данных, хотя есть менее известный вариант, который приведет вас в то же место.
Нахождение суммы квадратов для нескольких ячеек
Начните новый столбец в любом месте электронной таблицы Excel и пометьте его. Здесь мы выведем решение наших квадратов. Квадраты не обязательно должны быть рядом друг с другом, как и секция вывода; это может быть где угодно на странице.
Введите следующую формулу в первую ячейку нового столбца:
Отсюда вы можете вручную добавить буквенно-цифровую комбинацию столбца и строки или просто щелкнуть мышью. Мы будем использовать мышь, которая автоматически заполняет этот раздел формулы ячейкой A2.
Добавьте запятую, а затем мы добавим следующий номер, на этот раз из B2. Просто введите B2 в формулу или щелкните соответствующую ячейку, чтобы заполнить ее автоматически.
Закройте скобки и нажмите «Enter» на клавиатуре, чтобы отобразить сумму обоих квадратов. В качестве альтернативы, если вы можете продолжить здесь, добавьте дополнительные ячейки, разделив каждую запятую в формуле.
Чтобы применить формулу к дополнительным ячейкам, найдите маленький залитый квадрат в ячейке, содержащей решение нашей первой проблемы. В этом примере это C2.
Щелкните квадрат и перетащите его до последней строки пар чисел, чтобы автоматически сложить сумму остальных квадратов.
Нахождение суммы квадратов всего для нескольких ячеек
В нашем столбце «Сумма квадратов», который мы создали в предыдущем примере, в данном случае C2, начните вводить следующую формулу:
В качестве альтернативы мы можем просто добавить числа вместо ячеек в формулу, так как в любом случае мы попадем в одно и то же место. Эта формула выглядит так:
Вы можете изменять эти формулы по мере необходимости, изменяя ячейки, добавляя дополнительные числа или находя сумму квадратов, которых даже нет в вашей книге. И хотя легче следовать приведенному выше руководству, используя формулу SUMSQ, чтобы найти решение для нескольких квадратов, часто проще просто ввести быструю формулу, подобную этой, если вы не будете повторять ее на протяжении всей книги.
Сумма квадратов
Сумма квадратов встречается в ходе преобразования числовых и буквенных выражений. Как с ней работать?
Поскольку сумма квадратов является составной частью формул полного квадрата суммы и разности, можно попробовать применить одну из этих формул.
Формула полного квадрата суммы состоит из трёх слагаемых — сумма квадратов двух слагаемых плюс удвоенное произведение этих слагаемых. Следовательно, для получения полного квадрата к сумме квадратов двух выражений следует прибавить удвоенное произведение этих выражений, и, чтобы выражение не изменилось, вычесть это произведение:
Аналогично, для получения полного квадрата разности следует из суммы квадратов двух выражений вычесть удвоенное произведение этих выражений и тут же прибавить его:
Рассмотрим, как эти рассуждения могут быть применены на практике.
Теперь используем данные условия:
Эти рассуждения применяются, например, в приложении теоремы Виета, когда не решая квадратного уравнения, требуется найти сумму квадратов его корней и т.п.
Сумма квадратов
Что такое Сумма квадратов?
Сумма квадратов – это статистический метод, используемый в регрессионном анализе для определения разброса точек данных. В регрессионном анализе цель состоит в том, чтобы определить, насколько хорошо ряд данных может быть адаптирован к функции, которая может помочь объяснить, как был создан ряд данных. Сумма квадратов используется как математический способ найти функцию, которая лучше всего соответствует (меньше всего отличается) от данных.
Формула суммы квадратов:
Сумма квадратов также известна как вариация.
Что вам говорит сумма квадратов?
Допустим, цена закрытия Microsoft (MSFT) за последние пять дней составляла 74,01, 74,77, 73,94, 73,61 и 73,40 в долларах США. Сумма общих цен составляет 369,73 доллара, а средняя цена учебника, таким образом, будет 369,73 доллара / 5 = 73,95 доллара.
Сумма квадратов – это сумма квадратов вариации, где вариация определяется как разброс между каждым отдельным значением и средним значением. Чтобы определить сумму квадратов, расстояние между каждой точкой данных и линией наилучшего соответствия возводится в квадрат, а затем суммируется. Линия наилучшего соответствия минимизирует это значение.
Как посчитать сумму квадратов
Теперь вы можете понять, почему измерение называется суммой квадратов отклонений или для краткости суммой квадратов. Используя наш приведенный выше пример MSFT, сумму квадратов можно рассчитать как:
Добавление только суммы отклонений без возведения в квадрат приведет к числу, равному или близкому к нулю, поскольку отрицательные отклонения почти полностью компенсируют положительные отклонения. Чтобы получить более реалистичное число, необходимо возвести сумму отклонений в квадрат. Сумма квадратов всегда будет положительным числом, потому что квадрат любого числа, положительного или отрицательного, всегда положительный.
Пример использования суммы квадратов
Основываясь на результатах расчета MSFT, большая сумма квадратов указывает на то, что большинство значений дальше от среднего, и, следовательно, есть большая изменчивость в данных. Низкая сумма квадратов указывает на низкую изменчивость набора наблюдений.
В приведенном выше примере 1.0942 показывает, что колебания цены акций MSFT за последние пять дней очень низки, и инвесторы, желающие инвестировать в акции, характеризующиеся стабильностью цен и низкой волатильностью, могут выбрать MSFT.
Ключевые моменты
Ограничения использования суммы квадратов
Принятие инвестиционного решения о том, какие акции покупать, требует гораздо большего количества наблюдений, чем перечисленные здесь. Аналитику, возможно, придется работать с данными за годы, чтобы с большей уверенностью узнать, насколько высока или низка изменчивость актива. По мере того, как в набор добавляется больше точек данных, сумма квадратов становится больше, так как значения будут более разбросанными.
Существует два метода регрессионного анализа, в которых используется сумма квадратов: линейный метод наименьших квадратов и нелинейный метод наименьших квадратов. Метод наименьших квадратов относится к тому факту, что функция регрессии минимизирует сумму квадратов отклонения от фактических точек данных. Таким образом можно нарисовать функцию, которая статистически лучше всего подходит для данных. Обратите внимание, что функция регрессии может быть линейной (прямая линия) или нелинейной (кривая линия).
Калькулятор расчета суммы квадратов/кубов последовательных чисел
Последовательные числа — это члены натурального ряда, идущие друг за другом. Натуральные числа — это числа, которые мы используем для счета предметов. 1, 2, 3, 4 — последовательные элементы натурального ряда.
Числовые последовательности
Последовательность — упорядоченный набор чисел, который образуется по определенному закону. Существует множество самых разных числовых наборов, самым простым и понятным из которых считается натуральный ряд. Первые числа, которые дети учат в начальных классах, это члены натуральной последовательности:
Буквой n обозначается общий член последовательность, а для натурального ряда n считается и законом образования ряда. Закон последовательности — это форма записи принципа, по которому образуются члены ряда. Простой закон n означает, что номер элемента числового набора соответствует его значению. Первый элемент равен 1, второй — 2, десятый — 10. Для последовательности четных чисел, которая задается законом 2n, первый элемент набора будет равен 2, второй — 4, а десятый — 20. Набор нечетных чисел задается формулой 2n – 1, и в этом случай первый член ряда будет равен 1, второй — 3, десятый — 19.
Работа с числовыми наборами и законами их образования позволила математикам вывести формулы для определения сумм последовательных чисел натурального ряда.
Сложение последовательных чисел
Сумма первых n последовательных элементов натурального набора выражается следующей формулой:
Данная формула позволяет вычислить сумму натурального ряда от 1 до n. При сложении последовательных чисел не с первого элемента существует несколько хитростей, среди которых:
Рассмотрим пару примеров:
Правильность расчетов при помощи хитростей вы можете проверить на калькуляторе.
Сложение квадратов последовательных чисел
Более сложная задача состоит в суммирования последовательных чисел, возведенных в квадрат. Начало набора квадратов последовательных чисел выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100.
Для подсчета суммы первых пяти членов квадратной ряда 1 + 4 + 9 + 16 + 25, то есть n = 5, расчеты будут выглядеть как:
∑ = (5 × 6 × (2 × 5 + 1)) / 6 = 55
Используя данную формулу легко подсчитать общую сумму квадратов первых n квадратов.
Сложение кубов последовательных чисел
Для нахождения суммы первых n членов кубического ряда используется выражение:
Например, для нахождения значения ряда при n = 5, то есть выражения 1 + 8 + 27 + 64 + 125, расчеты будут выглядеть следующим образом:
∑ = (0,5 × 5 × 6) 2 = 15 2 = 225
При помощи этой простой формулы легко вычислить сумму кубов для сколь угодно большого n.
Наш калькулятор использует выше приведенные формулы для вычисления сумм квадратов или кубов натурального ряда для его первых n членов. Для расчетов вам необходимо выбрать тип калькулятора «Квадраты» или «Кубы», после чего ввести в ячейку количество элементов ряда. В теоретической части мы рассматривали сумму ряда из 5 членов, а при помощи онлайн-калькулятора легко рассчитать большие суммы.
Примеры использования
Рассчитаем сумму квадратов для 250 членов натурального ряда, то есть решим выражение 1 + 4 + 9 + … + 62 500. Для этого введем в форму калькулятора число 250 и получим мгновенный результат, равный 5 239 625.
Теперь вычислим сумму кубов для 250 членов натурального ряда, что будет равнозначно решению выражения 1 + 8 + 27 + … + 15 625 000. Изменим тип калькулятора и выберем «Куб», после чего введем в ячейку программу число 250. Наш результат не заставит себя ждать, и мы увидим 984 390 625.
Заключение
Для подсчета конечных сумм последовательных рядов используются простые формулы, которые, однако, не всегда удобно применять при повседневных расчетах. Используйте нашу программу для мгновенного подсчета значения квадратных и кубических рядов.