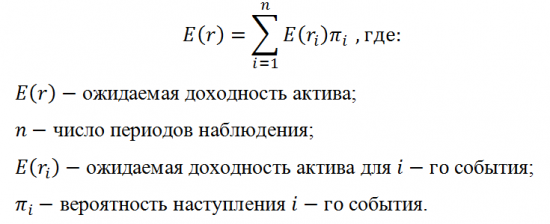Как посчитать стандартное отклонение портфеля

5 ключевых метрик инвестиционного портфеля

Чем большую доходность хочет инвестор, тем более рисковые инструменты ему придется использовать. Задача инвестора — найти такое сочетание активов, при котором соотношение доходности и риска станет наилучшим.

Рассмотрим 5 ключевых метрик, которые помогут в анализе инвестиционного портфеля. Эти параметры выдает большинство сервисов для анализа ценных бумаг и портфелей, в частности сайт Portfolio Visualizer, о работе с которым у нас есть статья.

📈 Среднегодовая доходность (CAGR)

Показывает среднегодовой темп роста портфеля на основе стартового и конечного капитала, а также срока инвестирования. Это среднегеометрическая доходность, учитывающая сложный процент, в отличие от средней арифметической доходности.

CAGR подходит, если инвестор не пополняет портфель и не выводит из него деньги в течение срока инвестирования. Если есть движение средств, то лучше использовать IRR — внутреннюю норму доходности

⏩ Стандартное отклонение (st. dev., σ)

Показывает, насколько волатильна доходность портфеля, то есть насколько он рискован. Считается как квадратный корень из дисперсии — разброса значений доходности от ее среднего значения.

Чем выше стандартное отклонение доходности актива или портфеля, тем выше риск. Чтобы снизить риск, в портфеле стоит сочетать инструменты с низким коэффициентом корреляции — о нем далее

🌀 Корреляция (correlation)

Показывает, насколько похоже ведут себя инструменты. Коэффициент корреляции может быть в диапазоне от −1 до 1.

Корреляция, близкая к единице, говорит о тесной взаимосвязи двух активов. Значение, близкое к нулю, показывает, что явной связи нет, а при значении около −1 активы движутся разнонаправленно.

Чем ниже коэффициент корреляции, тем лучше активы дополняют друг друга в портфеле. В теории, взяв два актива с корреляцией −1, можно достичь нулевого риска портфеля

🅱️ Бета (beta, β)

Показывает, как отдельный актив или портфель ведут себя относительно рынка. В случае с американскими акциями бета рассчитывается относительно индекса S&P 500, в случае с российскими акциями — относительно индекса Мосбиржи.

Бета 1 значит, что актив идентичен рынку. Если более 1, то актив коррелирует с рынком, но ведет себя более волатильно: сильнее растет или сильнее падает. Если бета от 0 до 1, то актив движется однонаправленно с рынком, а риск меньше рыночного.

При бете от 0 до −1 актив и рынок движутся в разные стороны, а актив стабильнее. При бете меньше −1 актив и рынок тоже движутся разнонаправленно, но актив волатильнее

💼 Коэффициент Шарпа (Sharpe ratio)

Показывает эффективность портфеля с точки зрения доходности и риска.

Считается так: (Доходность портфеля − Безрисковая процентная ставка) / Стандартное отклонение. Безрисковая ставка — это, например, доходность вкладов или векселей казначейства США.

Чем выше коэффициент Шарпа, тем большую прибыль извлекает инвестор на единицу риска и тем эффективнее стратегия

Источник

Стандартное отклонение доходности портфеля

При определении среднеквадратического или стандартного отклонения доходности портфеля возникает проблема, связанная с тем, что портфель состоит из двух и более активов (например, акций), каждый из которых имеет свое стандартное отклонение доходности. При этом каждый из активов вносит свой компонент риска в соответствии со своим удельным весом. Расчет общего риска как средневзвешенного по всем компонентам является в корне неправильным подходом. Это связано с тем, что существует определенная взаимосвязь между доходностью активов, которая может быть как прямой, так и обратной.

Формула

В общем виде формулу расчета стандартного отклонения портфеля, состоящего из N активов, можно представить в следующем виде:

где N – количество активов (ценных бумаг), входящих в портфель;

w_i – удельный вес i-го актива в портфеле;

σ (k_i) – стандартное (среднеквадратическое) отклонение доходности i-го актива;

Cov (k_i, k_j) – ковариация доходности i-го и j-го актива.

Представленную выше формулу можно преобразовать, используя формулу коэффициента корреляции.

После преобразования она приобретет следующий вид:

где R(k_i, k_j) – коэффициент корреляции доходности i-го и j-го актива.

Если развернуть это выражение для портфеля, состоящего из двух активов A и B, то оно будет выглядеть следующим образом:

Поскольку третье и четвертое слагаемые равны между собой, то формулу стандартного отклонения портфеля для двух активов можно записать в виде.

Для портфеля, состоящего из трех активов A, B и C, формула будет выглядеть так:

С увеличением количества активов уравнение будет становиться все более громоздкой.

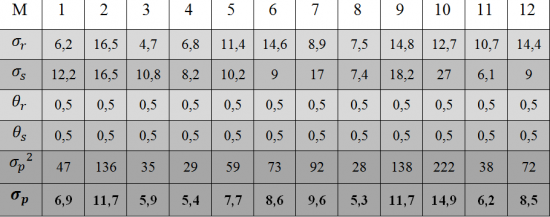
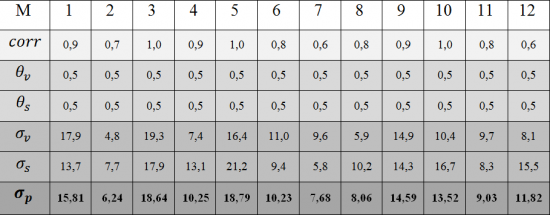
Пример

Рассчитаем стандартное отклонение доходности портфеля, который сформирован из трех ценных бумаг в следующих пропорциях:

Подставим исходные данные в приведенную выше формулу:

σ 2 _P = 0,252*92 + 0,352*122 + 0,42*72 + 2*0,25*0,35*0,6*9*12 + 2*0,25*0,4*(-0,45)*9*7 + 2*0,35*0,4*0,2*12*7 = 40,92

Таким образом, стандартное отклонение портфеля составит 6,4% (квадратный корень из 40,92).

Источник

Инвестиционный портфель. Доходность и риск инвестиционного портфеля.

Понятие инвестиционного портфеля.

Инвестиционный портфель представляет собой целенаправленно сформированную в соответствии с определённой инвестиционной политикой и выбранной управленческой стратегией совокупность вложений в различные инвестиционные объекты.

Главными параметрами при формировании и управлении инвестиционным портфелем, являются его ожидаемая доходность и риск. В связи с отсутствием возможности точного определения бедующей динамики вышеуказанных параметров, данные величины оцениваются, в первую очередь, на основе статистической информации за предыдущие периоды времени.

Ожидаемая доходность портфеля рассчитывается на основе ожидаемой доходности содержащихся в нём активов двумя способами.

Первый состоит в том, чтобы на основе прошлых статистических данных доходности актива рассчитать её среднеарифметическое значение по следующей формуле: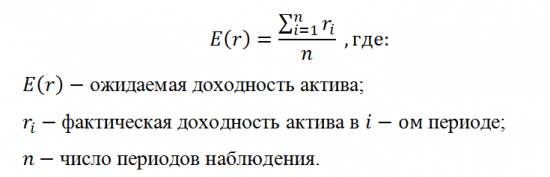

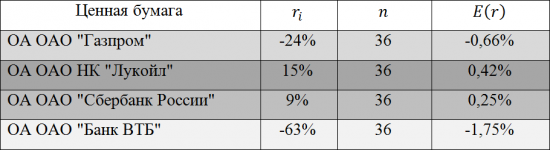
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности для 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка, на основании их ежемесячных доходностей за последние три года.

Из полученных значений следует, что наиболее привлекательной ценной бумагой являются обыкновенные акции ОАО НК «Лукойл», с ожидаемой доходностью в расчёте на месяц в 0,42%.

Второй заключается в учёте возможного будущего вероятностного распределения доходности актива. Ожидаемая доходность актива определяется как среднеарифметическая взвешенная, где весами являются вероятности каждого события, которые в сумме должны составлять 100% и рассчитывается по следующей формуле:

В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности несуществующей ценной бумаги.

Из полученного значения следует, сто ожидаемая доходность ОА ОАО «АлмаЗ», равна 0%.

Ожидаемая доходность инвестиционного портфеля при невозможности заимствования средств или осуществления коротких продаж.

Формируемый инвестиционный портфель состоит из нескольких ценных бумаг, каждая из которых обладает своей ожидаемой доходностью, среднеарифметическая ожидаемая доходность которых, является ожидаемой доходностью инвестиционного портфеля и рассчитывается по следующей формуле:

Удельный вес n-ой бумаги в портфеле рассчитывается, как отношение её стоимости к стоимости всего портфеля по следующей формуле:

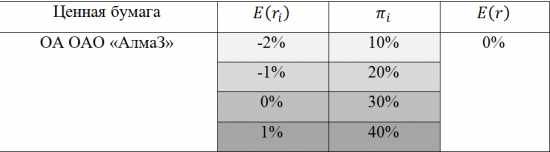
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка, на основании их ежемесячных доходностей за последние три года.

Из полученного в ходе расчётов значения следует, что ожидаемая доходность состоящего из вышеуказанных 4 ценных бумаг инвестиционного портфеля, равна 0,23%.

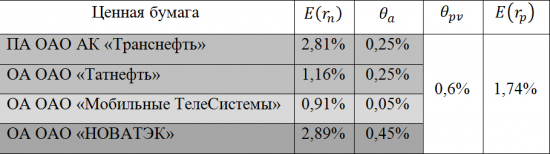
Ожидаемая доходность инвестиционного портфеля при возможности заимствования средств.

Формирование инвестиционного портфеля может осуществляться не только на собственные средства, но и на заёмные, в результате чего, возникает эффект финансового рычага и увеличивается ожидаемая доходность портфеля. В этом случае, денежные средства занимаются под более низкую процентную ставку и размещаются в потенциально более доходный актив, образуя портфель, состоящий фактически из двух активов, приобретаемой ценной бумаги и заимствованных средств. Ожидаемая доходность портфеля рассчитывается по следующей формуле:

В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка, на основании их ежемесячных доходностей за последние три года. В качестве заёмных средств будем использовать краткосрочный кредит (сроком на 1 месяц) с простой процентной ставкой заимствований, равной 12 процентам годовым.

Из полученных в ходе расчётов значений следует, что ожидаемая доходность инвестиционного портфеля составила 1,74 процента. За счёт привлечения заёмных финансовых ресурсов, доходность портфеля была увеличена на 0,8 процента, что говорит об эффективности использования заёмных средств, в формировании инвестиционного портфеля.

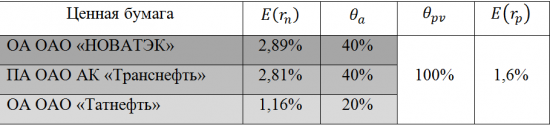
Ожидаемая доходность инвестиционного портфеля при использовании только заёмных средств.

Формирование инвестиционного портфеля может осуществляться исключительно за счёт заёмных средств, что имеет только теоретическое значение, поскольку получение кредита связано с определённым обеспечением полученных средств. Поэтому ожидаемый результат необходимо оценивать относительно тех средств, которые в этом случае блокируются.

Ожидаемая доходность портфеля с использованием только заёмных средств рассчитывается по следующей формуле:

В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 3 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка. Расчёт будет вестись на основании их ежемесячных доходностей за последние три года, а доля заёмных средств в инвестиционном портфеле, будет составлять 100 процентов.

Из полученных в ходе расчётов значений следует, что путём выбора инвестиционных объектов с наибольшими ожидаемыми доходностями возможно формирование инвестиционного портфеля за счёт только заёмных средств, а также рассчитывать на получение дохода от подобной операции. Так, ожидаемая доходность используемого в данном примере инвестиционного портфеля, составила 1,6 процента.

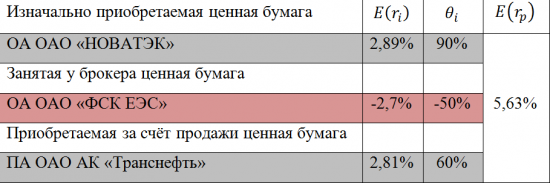
Ожидаемая доходность инвестиционного портфеля при возможности коротких продаж.

Формирование инвестиционного портфеля может осуществляться с использованием короткой продажи занятого у брокера актива без процентов и резервирования средств, по обеспечение другими активами, находящимися в инвестиционном портфеле. Ожидаемая доходность портфеля в данном случае, будет рассчитываться по следующей формуле:

В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка. Расчёт будет вестись на основании их ежемесячных доходностей за последние три года, а доля занятых у брокера ценных бумаг будет равна 30% стоимости портфеля. Также, в данном примере, брокер не взимает процентов за предоставленные ценные бумаги и не резервирует часть средств, в качестве их обеспечения.

Из полученных в ходе расчёта значений следует, что использование занятых у брокера и предназначенных для продажи ценных бумаг, позволило увеличить ожидаемую доходность инвестиционного портфеля до 5,63 процентов. На практике, допускается продажа заёмных ценных бумаг в том случае, если их ожидаемая доходность не превышает доходности приобретаемых ценных бумаг. В противном случае, велик риск получения убытков от данной операции.

Риск инвестиционного портфеля

Основополагающими мерами риска финансового актива являются такие показатели как стандартное отклонение (волатильность) и дисперсия его доходности, которые говорят о степени возможного разброса фактической доходности вокруг его средней доходности. Данные показатели можно определить на основе прошлых статистических данных доходности актива.

Дисперсия является показателем рассеяния фактических значений доходности акции вокруг её средней доходности и рассчитывается по следующей формуле:

Однако, размерность дисперсии представляет собой квадрат доходности ценной бумаги. Если в формуле учитывается доходность в процентах, а размерность дисперсии, это процент в квадрате, поэтому показателем такой размерности не всегда удобно пользоваться. Поэтому из дисперсии извлекают корень и получают стандартное отклонение последующей формуле: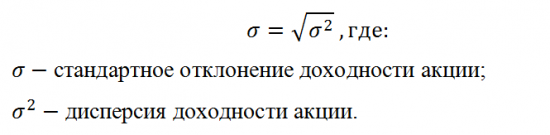

В отличие от ожидаемой доходности инвестиционного портфеля его риск не является средневзвешенной величиной стандартных отклонений доходностей содержащихся в нем ценных бумаг. Данное несоответствие связанно с различной реакцией ценных бумаг на изменение рыночной конъюктуры, в результате чего, стандартные отклонения доходности различных ценных бумаг в ряде случаев будут погашать друг друга, что приведёт к снижению риска инвестиционного портфеля. В связи с этим, при подборе ценных бумаг в портфель инвестиций принято определять степень их взаимосвязи на основании значений ковариации и коэффициента корреляции.

Из полученных значений можно сделать следующие выводы: во всех рассматриваемых временных окнах наблюдается положительная ковариация, свидетельствующая об однонаправленном движении рассматриваемых ценных бумаг.

Коэффициент корреляции отражает степень зависимости двух ценных бумаг. В отличие от ковариации, данный показатель не зависит от единиц измерения доходностей ценных бумаг и не характеризует рассеяние доходностей вокруг средних значений. В результате чего ковариация не позволяет получить наглядное отражение степени взаимосвязи между инструментами.

Из полученных в ходе расчёта значений следует, что в 91% случаев корреляция является положительной, следовательно, динамика доходностей ценных бумаг является зависимой. В случае снижения котировок одной ценной бумаги, вторая будет следовать за ней.

После определения взаимосвязи меду ценными бумагами путём расчёта ковариации и коэффициента корреляции можно приступить к подбору инвестиционных объектов и определению совокупного риска портфеля, рассчитываемого несколькими способами, ключевые из которых будут далее рассмотрены.

Риск портфеля состоящего из двух активов определяется на основании их ковариации, удельных весов и стандартных отклонений по следующей формуле:

В качестве примера определения риска инвестиционного портфеля состоящего из 2 ценных бумаг, осуществим расчёт риска портфеля состоящего из ОА ОАО «Газпром» и ОА ОАО «Лукойл». Расчёт ожидаемого риска будет проводиться на их ежемесячных доходностях за последние восемь лет.

Из полученных значений можно сделать следующие выводы. Первый, наименьший риск инвестиционного портфеля показывают декабрьские вложения (порядка 3 процентов), майские наибольший (10,5 процентов). Второй, наибольшее влияние на риск портфеля оказывает волатильность содержащихся в нём инструментов.

Другой способ расчёта риска портфеля из двух ценных бумаг, применяется в том случае, если корреляция их доходностей равна или близка к значению +1. Таким образом, риск инвестиционного портфеля представляет собой средневзвешенный риск входящих в него ценных бумаг и рассчитывается по следующей формуле: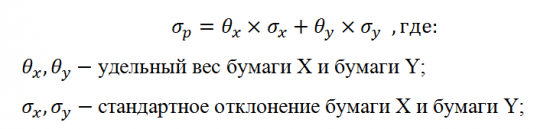

В качестве примера использования данного способа, осуществим расчёт ожидаемого риска на основании доходностей обыкновенных акций ОАО «Банк ВТБ» и ОАО «Сбербанк России», являющихся представителями одного сектора с наибольшей корреляцией доходностей (0,835).

Из полученных значений следует, что в данном случае диверсификация портфеля не привела к сокращению совокупного риска инвестиционного портфеля, а только усреднила его. Следственно, при изменении рыночной конъюктуры доходности ценных бумаг будут изменяться в прямой зависимости в одном и том же направлении.

Объединив в определённой пропорции данные валюты в инвестиционном портфеле, можно добиться безрисковых вложений, также не приносящих инвестиционного дохода и направленных на сохранение капитала и его защиту от валютных рисков.

Наиболее эффективным способом формирования хорошо диверсифицированного инвестиционного портфеля, является распределение капитала между ценными бумагами, значение корреляции между которыми наиболее близко к нейтральному значению.

Риск портфеля из двух активов с отсутствием корреляции между ними, определяется по следующей формуле: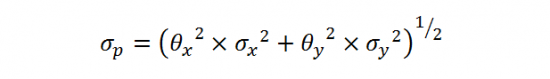

В качестве примера использования данного метода, осуществим расчёт риска инвестиционного портфеля, состоящего из 2 ценных бумаг с наиболее близким к 0 значением корреляции их доходностей. Наиболее подходящими для поставленной задачи, являются обыкновенные акции ОАО «Ростелеком» и ОАО «Северсталь». Совокупная корреляция между их ежемесячными доходностями за последние восемь лет, равна 0,15.

Из полученных в ходе расчётов значений, можно сделать следующий вывод, риск сформированного нами инвестиционного портфеля находится в диапазоне от 5,3% до 14,9%, в зависимости от месяца его ориентировочного формирования. Однако сказать, как на практике поведёт себя одна бумага, по отношению к другой не представляется возможным.

Риск инвестиционного портфеля из нескольких ценных бумаг.

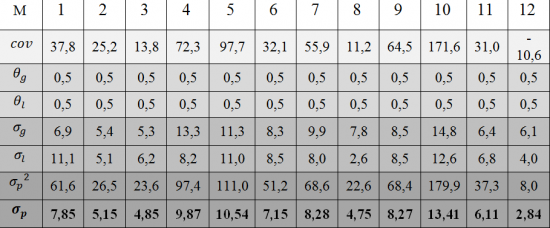
В заключение отражения способов определения риска портфеля, осуществим расчёт риска для инвестиционного портфеля из нескольких ценных бумаг. Осуществлять оценку данного показателя будем на основе ежемесячных доходностей ценных бумаг трёх крупнейших эмитентов. А именно, обыкновенных акций ОАО «Банк ВТБ», ОАО НК «Лукойл» и ОАО «Сбербанк России».

———База для осуществления расчётов в следующем посте (не вместилась)———

Опираясь на полученные в ходе расчётов значения данных показателей, перед управляющим стоит задача подбора инвестиционных объектов с целью формирования эффективного и целесообразного портфеля. Главной ориентацией которого, является наибольшая ожидаемая доходность при наименьшем или допустимом уровне риска.

Исходя из преследуемых управляющим целей и его отношения к риску, принято классифицировать инвестиционные портфели следующим образом:

Управление инвестиционным портфелем представляет собой совокупность методов и технологических возможностей, применяемых к различным ценным бумагам, и направленных на сохранение первоначальных стоимости инвестиционных вложений, достижение максимального уровня дохода при наименьшем уровне риска и обеспечение общей инвестиционной направленности портфеля.

Управление портфелем инвестиций может быть представлено в качестве активной или пассивной моделей, применяемых исходя из определённой инвестиционной направленности портфеля.

Активная модель управления инвестиционным портфелем предполагает постоянную систематическую работу инвестиционных менеджеров, направленную на повышение эффективности инвестиционной деятельности, путём подбора ценных бумаг с наибольшими ожидаемыми доходностями при допустимом уровне риска. Точное выявление и своевременная покупка недооценённых рынком ценных бумаг, позволяют получить гораздо более высокие результаты, по сравнению с пассивной моделью.

Пассивная модель управления инвестиционным портфелем заключается в формировании хорошо диверсифицированного рыночного портфеля, с заранее фиксированным уровнем риска, рассчитанным на длительный период времени. Данная модель управления является наиболее привлекательной на развитых фондовых рынках с относительно стабильной конъюнктурой в условиях умеренного экономического роста.

Наиболее распространёнными стратегиями управления портфелем ценных бумаг пассивной модели являются:

1) Стратегия копирования индекса – заключается в формировании портфеля, состав, структура и характеристики которого максимально схожи с составом, структурой и характеристиками выбранного фондового индекса. Основной задачей данной стратегии является минимизация стандартного отклонения разности между доходностями сформированного портфеля и копируемого индекса.
Использование стратегии копирования фондового индекса сопряжённо с высокими транзакционными издержками, возникающими в процессе формирования портфеля и связанными с приобретением большого количества содержащихся в выбранном индексе ценных бумаг. Управляющие, с целью минимизации вышеуказанных издержек прибегают к частичному копированию индекса, путём вложений в ценные бумаги, динамика которых наиболее схожа с динамикой фондового индекса.

2) Стратегия скольжения по кривой доходности – представляет собой краткосрочные вложения в долгосрочные долговые ценные бумаги (облигации), характеризующиеся наибольшей годовой доходностью по сравнению с их краткосрочными аналогами. Данная стратегия применяется управляющими с ограниченными инвестиционными горизонтами, предполагающими сохранение восходящей формы кривой доходности в будущем.

3)Стратегия иммунизации инвестиционного портфеля – заключается в выборе долговых ценных бумаг (облигаций) с таким инвестиционным горизонтом, в течение которого на финансовом рынке прогнозируется стабильная процентная ставка, не приводящая к изменению стоимости подобранных ценных бумаг. Так же, в процессе управления сформированным портфелем происходит реинвестирование купонных доходов, позволяющее застраховать портфель от изменения стоимости содержащихся в нём облигаций, вызванного незначительным изменением процентной ставки.

Традиционные механические схемы управления портфелем ценных бумаг имеют следующие основные разновидности:

1) Схема дополнительной фиксированной суммы – характеризуется фиксированной суммой вложений в ценные бумаги через фиксированные временные интервалы. Цикличность колебаний курсов ценных бумаг позволяет получать прибыль за счёт прироста их курсовой стоимости. Реализуется путём приобретения наибольшего количества ценных бумаг при значительном понижении их котировок, и наименьшего количества при повышении соответственно.
Данная схема управления является крайне пассивной и наиболее рискованной в периоды экономической нестабильности, подразумевая усреднение позиций в ценных бумагах с отрицательной доходностью, что приводит к потере значительной стоимости портфеля при наступлении экономического кризиса.

2) Схема фиксированной спекулятивной суммы – подразумевает разделение портфеля ценных бумаг на консервативную и спекулятивную части. Величина спекулятивной части формируется из высокорискованных ценных бумаг и поддерживается на изначально установленном уровне.

3) Схема фиксированной пропорции – так же, как и схема фиксированной спекулятивной суммы подразумевает разделение портфеля на две части, первая из которых должна находиться в заданной пропорции по отношению ко второй.

4) Схема плавающих пропорций – заключается в формировании портфеля ценных бумаг с рядом установленных взаимосвязанных соотношений между спекулятивной и консервативной частью.

Материал из главы моей дипломной работы, пользуйтесь на здоровье.
Продолжение следует, удачной торговли!

Источник