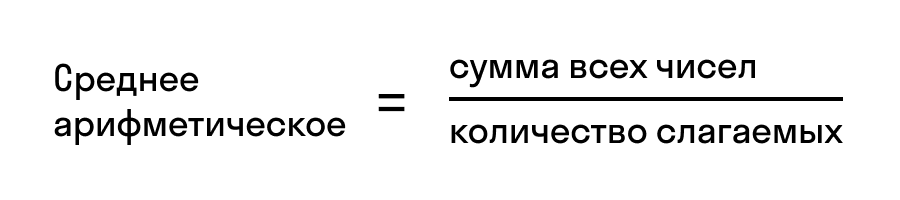Как посчитать среднюю арифметическую величину
8.3. Средние величины в статистике
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
Таблица 8.2 – Результаты опроса работников офиса
Простая формула, чтобы подсчитать среднее арифметическое
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
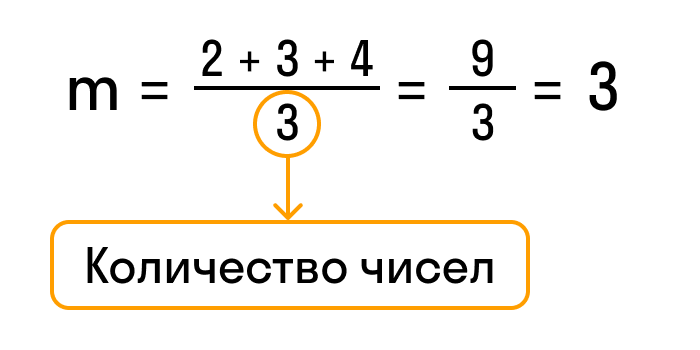
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Как вычислить среднее арифметическое
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Как рассчитать среднюю величину
Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.
После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.
Алгоритм решения задач на расчет средней величины
А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.
Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.
В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).
Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.
В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.
В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.
Рассмотрим на примерах использование данного алгоритма.
Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.
А. Так как данные представлены в строчку то используем простой способ расчета.
Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.
Средний размер пенсии пенсионера составляет 9208,3 рубля.
Задача 2. Рассчитать средний размер детских выплат по следующим данным
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.
Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.
В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.
Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.
Задача 3. Рассчитать среднюю себестоимость единицы изделия
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1 ), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.
Средняя себестоимость единицы изделия составила 314,4 рубля.
Задача 4. Рассчитать среднюю число пропусков одного студента
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.
Составляем логическую формулу расчета среднего числа пропусков одного студента.
Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.
Среднее число пропусков одного студента 13,8 дня.