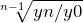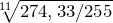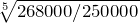Как посчитать среднегодовые темпы роста

Формула среднегодового темпа роста

Понятие темпа роста

Математическая статистика часто использует формулу темпа роста. Темп роста определяет интенсивность изменения (динамики) определенного явления.

Для того, что бы определить темп роста требуются следующие показатели:

Для расчета среднегодового темпа роста применяется временной интервал, который равен месяцу.

Понятие темп роста применяется во многих сферах (экономика, финансы, статистика, промышленность и др.). Темп роста является статистической величиной, позволяющей провести анализ:

Для вычисления темпа роста происходит сравнение значений, которые получены через выбранные промежутки времени.

Формула темпа роста

В общем виде, при наличии базисного и текущего показателя, формула темпа роста выглядит следующим образом:

Тр=Птек/Пбаз

Здесь Тр – темп роста,

Птек – показатель текущего периода,

Пкп – показатель базисного периода.

Что бы получить более наглядный результат, полученный ответ умножают на 100%, что позволяет выразить темп роста в процентах.

Порядок расчета среднегодового темпа роста

Для расчета среднего темпа роста требуется определить период, за который он будет рассчитан. В большинстве случаев таким периодом является календарный год или показатель, кратный ему.

Темп роста является относительным понятием, поскольку определяет изменение определенных величин по отношению к какому-либо начальному значению. Для расчета среднегодового темпа роста определяется начальное значение на 1 января исследуемого года. Расчет среднегодового темпа роста может проводиться в соответствии с величинами:

Общая формула расчета среднегодового темпа роста выглядит следующим образом:

Тр ср =

Здесь n– количество месяцев (лет),

y0 – базисный показатель (например, на 1 января)

Особенности формулы среднегодового темпа роста

Формула среднегодового темпа роста использует в качестве базисного показателя численную величину, которая характеризует изучаемое явление и определяется по концу предыдущего года. Таким образом, базисная величина – это величина показателя на 1 января того года, для которого требуется определить темп роста.

При расчете формулы среднегодового темпа роста коэффициентом, базовый показатель принимают за единицу или 100 (если расчет осуществляется в процентах). В процессе вычисления базовых темпов роста на каждый месяц в году все показатели по окончанию каждого месяца должны соотноситься с базовым показателем (на 1 января).

При определении цепных показателей, за базовый показатель принимается показатель предыдущего периода, поэтому при расчете формула среднегодового темпа роста удобнее рассчитывается с помощью цепных показателей.

Значение среднегодового темпа прироста

За анализируемый период формула среднегодового темпа роста принимает календарный год, то есть промежуток с 1 января по 31 декабря. Для этого необходимы данные в абсолютном значении на конец каждого месяца. Всего должно быть 13 значение (базовый показатель и 12 показателей за каждый месяц).

Формула среднегодового темпа роста имеет значение, поскольку при ее расчете по нескольким годам можно получить результат для дальнейшего анализа и учета сезонных колебаний. Сам среднегодовой темп роста свободен от влияния фактора сезонности.

Примеры решения задач

Задание

Рассчитайте среднегодовой темп роста по показателям, представленным за год:

Январь – 240, февраль – 256, март – 258, апрель – 259, май – 262, июнь – 275, июль – 278, август – 279, сентябрь – 282, октябрь – 284, Ноябрь – 288, декабрь – 291.

РешениеРассчитаем средний уровень ряда динамики:

Пср = (240+256+258+259+262+275+278+279+282+284+288+291) / 12 = 271 – среднее значение с 1 по 12 месяц.

Формула среднегодового темпа роста для решения данной задачи:

Тр ср =

Тр ср =

Задание

Рассчитать среднегодовой темп роста и прироста, по условным данным объема импорта государства:

2011 год – 250 усл. ед.,

2012 год – 258усл. ед.,

2013 год – 262усл. ед.,

2014 год – 248усл. ед.,

2015 год – 259усл. ед.,

2016 год – 268усл. ед.,

РешениеФормула среднегодового темпа роста для решения данной задачи:

Тр ср =

Тр ср =

Вывод:За период с 2011 по 2016 год ежегодно объем импорта государства в среднем возрастал на 1,014 единиц.

Источник

Формула среднего темпа роста

Сущность темпа роста

Математика и статистика, а также экономические науки часто используют в расчетах формулу темпа роста.

Формула среднего темпа роста требует следующих показателей:

Для расчета, например среднегодового темпа роста, применяют временной интервал, равный месяцу.

Понятие темп роста используется во многих областях (в экономике, финансовом анализе, статистике, промышленности и др.). Темп роста — статистическая величина, которая дает возможность анализировать:

Формула среднего темпа роста предполагает расчет и сравнение значений, получаемых за выбранные временные промежутки.

Общая формула темпа роста

При определенных базисных и текущих величинах формула темпа роста в общем виде выглядит таким образом:

Тр=Птек/Пбаз

Здесь Тр – темп роста,

Птек – показатель текущего периода,

Пкп – показатель базисного периода.

Для получения более наглядного результата, полученный ответ умножается на 100% для выражения темпа роста в процентном соотношении.

Порядок расчета среднего темпа роста

Для вычисления среднего темпа роста в первую очередь определяется период, за который онрассчитывается. Чаще всего таким периодом может быть календарный год или кратные ему показатель.

Темп роста — относительное понятие,определяющее изменение соответствующих значений по отношению к определенному начальному показателю. Формула среднеготемпа роста за год может определяться исходя из начального значения на 1 января рассматриваемого года. Вычисление среднего темпа роста проводится по следующим величинам:

Формуласреднего темпа роста выглядит следующим образом:

Тр ср =

Здесь n– количество (лет, месяцев),

y0 – базисный показатель (например, на 1 января)

Особенности расчета среднего темпа роста

Формула среднего темпа роста в качестве базисного показателя использует числовую величину, характеризующую исследуемое явление и определяющуюся на конец предыдущего года. Базисная величина может быть показателем на 1 января того года, для которого требуется определить средний темп роста.

Например, в расчете формулы среднего годового темпа роста с помощью коэффициентов, базисный показатель может приниматься за единицу или 100 (в случае процентных расчетов). В ходе вычисления базовых темпов роста за каждый месяц все показатели конца каждого месяца соотносятся с базовым показателем (например, показателем 1 января).

В процессе определенияцепных показателей, базовым показателем может быть показатель предыдущего периода. По этой причине при вычислениях формула среднего темпа роста удобнее рассчитывается посредством цепных показателей.

Формула среднего темпа роста имеет огромное значение, так как при ее расчетах по нескольким годам (месяцам) можно получить результат для последующего учета и анализа сезонных колебаний.

Примеры решения задач

Задание

Рассчитайте средний темп роста за год по следующим показателям:

Январь – 255, февраль – 256, март – 258, апрель – 268, май – 262, июнь – 275, июль – 282, август – 279, сентябрь – 294, октябрь – 284, Ноябрь – 288, декабрь – 291.

РешениеРассчитаем средний уровень ряда динамики:

Пср = (255+256+258+268+262+275+282+279+294+284+288+291) / 12 = 274,33 – среднее значение за год.

Формула среднеготемпа роста за год для решения данной задачи:

Тр ср =

Тр ср =

Вывод. Мы видим, что за рассматриваемый год рост показателя — 1,007.

Задание

Рассчитать средний темп роста выручки предприятия поданным условнымпоказателям:

1 период – 250 000 руб.,

2 период – 258 000 руб.,

3 период – 262 000 руб.,

4 период – 248 000 руб.,

5 период – 259 000 руб.,

6 период – 268 000 руб.

РешениеИспользуем следующую формулу среднеготемпа роста для решения данной задачи:

Тр ср =

Тр ср =

Источник

Среднегодовой темп роста (AAGR)

Среднегодовое увеличение стоимости инвестиционного актива, портфеля или денежного потока

Каков средний годовой темп роста (AAGR)?

Среднегодовой темп роста (AAGR) — это среднегодовое увеличение стоимости инвестиционного актива, портфеля или денежного потока. Он определяется путем взятия среднего численного значения указанных или рассчитанных темпов роста в годовом исчислении.

Среднегодовые темпы роста используются для многих областей — например, в экономике, в которой AAGR дает четкое представление об изменениях в экономических показателях (например, фактических темпах роста ВВП).

AAGR обычно выражается в процентах.

Резюме

Использование среднегодового темпа роста (AAGR)

AAGR полезен при оценке долгосрочных тенденций. Он актуален практически для любой формы анализа финансовых показателей, таких как темпы роста доходов, продаж, денежных потоков, расходов и т. Д., Чтобы дать инвесторам представление о направлении, в котором движется фирма. AAGR в среднем показывает, какой была годовая прибыль.

Формула

Среднегодовой темп роста = [(Growth Rate)_y + (Growth Rate)_y+1 + … (Growth Rate)_y+n] / N

Как рассчитывается AAGR

AAGR — это эталон для расчета средней рентабельности инвестиций за несколько лет. По сути, это базовые средние темпы роста доходности за последовательность периодов (лет).

Чтобы вычислить среднее значение, необходимо вычислить скорость роста для каждого отдельного периода времени в ряду. Это можно сделать, используя следующую базовую формулу:

Процент темпов роста = ((EV / BV) — 1) x 100%

После того, как процентные показатели темпов роста для каждого периода времени были рассчитаны, они складываются и делятся на общее количество периодов времени, что дает AAGR.

Один момент, который всегда следует учитывать, — это то, что используемые периоды должны быть равными по длине при расчете темпов роста. Эти периоды времени могут быть год к году, месяц к месяцу, квартал и т. Д., В зависимости от конкретных потребностей человека или фирмы, вычисляющей темпы роста.

Пошаговый пример

Учитывая следующие годовые доходы компании ABC:

Год 1: 250 000 долларов

Год 2: 356 000 долларов

Год 3: 390 000 долларов

Год 4: 395000 долларов

Год 5: 400 000 долларов

Год 6: 358 000 долларов

Год 7: 320 000 долларов

Используя приведенную выше формулу темпа роста, темпы роста с 1 по 7 год можно рассчитать как:

Y1: 0, потому что нет предыдущего периода времени

А AAGR рассчитывается как:

Сумма темпов роста = [42,4% + 9,7% + 101,3% + 101,3% + (-10,5%) + (-10,6%)]

Среднегодовой темп роста компании ABC составляет 33,4%.

Ограничения на среднегодовой темп роста (AAGR) в финансовом анализе

Рассмотрим портфель, который вырастет на 25% в первый год и на 12% в следующий год. Среднегодовой темп роста (AAGR) будет рассчитан как 18,5%. Колебания доходности портфеля между началом первого года и концом года не учитывают расчет среднегодовых темпов роста.

Это может привести к определенным ошибкам в оценке. Поскольку AAGR представляет собой среднее значение годовой доходности, этот показатель не дает оценки общего риска, связанного с инвестициями, на основании нестабильности их цены. В принципе, AAGR можно оценить для любых инвестиций; однако он не будет указывать на потенциальный риск инвестиций.

Кроме того, AAGR не учитывает эффекты начисления процентов, поскольку это линейный показатель. Анализ может показать, что инвестиции росли в среднем на n процентов в год, при этом не учитывались колебания, которые могли произойти в течение временного ряда.

AAGR, идеально подходящий для отображения тенденций, также может вводить в заблуждение инвесторов, поскольку не отражает адекватно меняющиеся финансовые тенденции. Также можно переоценить рост инвестиций.

Дополнительные ресурсы:

Finansistem является официальным поставщиком глобальной программы сертификации специалистов по финансовому моделированию и оценке (FMVA) ™, призванной помочь каждому стать финансовым аналитиком мирового уровня. Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:

Источник

CAGR, Среднегодовой темп роста

Калькулятор CAGR

Чтобы рассчитать CAGR, введите начальное значение, конечное значение и количество периодов, в течение которых инвестиции выросли.

Формула расчёта CAGR

Пример

Если ваши инвестиции выросли с 100.000 рублей до 250.000 рублей за последние пять лет, то совокупный годовой темп роста ваших инвестиций составил 20,11% в год. Калькулятор CAGR также можно использовать для определения темпа роста, который вам понадобится в будущем для достижения инвестиционных целей, поставленных сегодня. Например, если у вас сегодня есть 1000 долларов, и через пять лет вы хотите, чтобы ваши инвестиции составляли 2500 долларов, вам нужно будет найти такие способы инвестирования, которые, как ожидается, могут приносить по 20,11% в год.

Где применяется калькулятор CAGR

Среднегодовой темп роста применяется в различных участках личных финансов. Он часто используется для расчета среднего роста отдельных инвестиций за определенный период. CAGR может применяться при сравнении доходности капитала с облигациями или депозитами. Кроме того, его можно использовать для сравнения результатов деятельности двух компаний и прогнозирования их будущего роста на основе их исторических данных.

Ограничение CAGR

CAGR не учитывает волатильность. Он рассчитывает только средний процент возврата, поэтому значения CAGR никогда не должны рассматриваться как единственный инструмент для оценки возврата инвестиций.

Почему CAGR так важен

Хотя среднегодовая доходность является общепринятой для взаимных фондов, CAGR является всё же лучшим показателем доходности инвестиций с течением времени.

Усреднение результатов за 1-й и 2-й год за два года дает нам среднюю доходность 4% [(-25 + 33) / 2], но это не совсем точно отражает то, что произошло на самом деле. Мы начали с 1000 рублей и закончили тоже на 1000 рублей, а значит наша доходность равна 0%.

Т.е. ещё раз. В данном примере, среднегодовая доходность: 4%, а CAGR равен 0%, что конечно правильнее.

Нас 1.5 человека, но мы уже утираем нос некоторым проектам. Скоро будут ещё люди, что же станет тогда?

Источник

Как рассчитать темп роста в процентах

tempy_rosta.jpg

Похожие публикации

Важнейшим показателем эффективности производства в анализе финансовой ситуации в компании является показатель темпа роста. Поговорим об особенностях его расчета.

Как рассчитать темп роста: формула

Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.

Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.

ТР = П_т / П_б х 100%,

где П_к и П_б – показатели значений текущего и базового периодов.

Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:

ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;

ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;

ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.

Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:

Объем выпуска в тыс. руб.

Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.

Как рассчитать цепные темпы роста

Рассмотрим пример расчета базисного и цепного темпов роста:

Период

Объем в тыс.руб.

Темп роста в %

базисный

цепной

Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).

Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.

Как рассчитать темпы прироста

Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:

Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:

Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.

Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:

Источник