Как посчитать сложность алгоритма python
Нотация Big O и анализ алгоритмов с примерами Python
Анализ алгоритмов относится к анализу сложности различных алгоритмов и поиску наиболее эффективного алгоритма для решения поставленной задачи. Big-O Notation – это статистическая мера, используемая для описания сложности алгоритма.
В этой статье мы кратко рассмотрим анализ алгоритмов и нотацию Big-O. Мы увидим, как нотация Big-O может быть использована для определения сложности алгоритма с помощью различных функций Python.
Почему важен Анализ Алгоритмов?
Чтобы понять, почему важен анализ алгоритмов, воспользуемся простым примером.
Предположим, менеджер дает задание двум своим сотрудникам разработать алгоритм на языке Python, который вычисляет факториал числа, введенного пользователем.
Алгоритм, разработанный первым сотрудником, выглядит так:
Аналогично, второй сотрудник также разработал алгоритм, который вычисляет факториал числа. Второй сотрудник использовал рекурсивную функцию для вычисления факториала программы, как показано ниже:
Менеджер должен решить, какой алгоритм использовать. Для этого он должен найти сложность алгоритма. Один из способов сделать это-найти время, необходимое для выполнения алгоритмов.
Вывод говорит, что алгоритм занимает 9 микросекунд (плюс/минус 45 наносекунд) на цикл.
Аналогично выполните следующий сценарий:
Второй алгоритм, включающий рекурсию, занимает 15 микросекунд (плюс/минус 427 наносекунд).
Время выполнения показывает, что первый алгоритм работает быстрее по сравнению со вторым алгоритмом, включающим рекурсию. Этот пример показывает важность алгоритмического анализа. В случае больших входных данных разница в производительности может стать более значительной.
Однако время выполнения не является хорошей метрикой для измерения сложности алгоритма, поскольку оно зависит от аппаратного обеспечения. Необходим более объективный анализ метрик сложности алгоритмов. Вот тут-то и вступает в игру нотация Big O.
Анализ алгоритмов с нотацией Big-O
Нотация Big-O-это метрика, используемая для определения сложности алгоритма. В принципе, обозначение Big-O означает связь между входными данными алгоритма и шагами, необходимыми для выполнения алгоритма. Он обозначается большой буквой “О”, за которой следуют открывающая и закрывающая скобки. Внутри круглой скобки связь между входными данными и шагами, выполняемыми алгоритмом, представлена с помощью буквы “n”.
Например, если существует линейная зависимость между входными данными и шагом, выполняемым алгоритмом для завершения его выполнения, то используемая нотация Big-O будет O(n). Аналогично, обозначение Big-O для квадратичных функций равно O(n^2)
Ниже приведены некоторые из наиболее распространенных функций Big-O:
| Постоянный | O(c) |
| Линейный | O(n) |
| Квадратный | O(n^2) |
| Кубический | O(n^3) |
| Экспонентный | O(2^n) |
| Логарифмический | O(log(n)) |
| Логарифмический линейный | O(nlog(n)) |
Чтобы получить представление о том, как вычисляется нотация Big-O, давайте рассмотрим некоторые примеры постоянной, линейной и квадратичной сложности.
Постоянная сложность (O(C))
Сложность алгоритма называется постоянной, если шаги, необходимые для завершения выполнения алгоритма, остаются постоянными, независимо от количества входных данных. Постоянная сложность обозначается через O(c), где c может быть любым постоянным числом.
Давайте напишем простой алгоритм на Python, который находит квадрат первого элемента в списке и затем выводит его на экран.
Если вы нарисуете линейный график с переменным размером входных данных items на оси x и количеством шагов на оси y, вы получите прямую линию. Чтобы визуализировать это, выполните следующий сценарий:
Линейная сложность (O(n))
Сложность алгоритма называется линейной, если шаги, необходимые для завершения выполнения алгоритма, увеличиваются или уменьшаются линейно с числом входов. Линейная сложность обозначается через O(n).
В этом примере давайте напишем простую программу, которая выводит все элементы списка на консоль:
График линейной сложности с входами по оси x и количеством шагов по оси x выглядит следующим образом:
Еще один момент, который следует отметить здесь, заключается в том, что в случае огромного количества входных данных константы становятся незначительными. Например, взгляните на следующий сценарий:
Мы можем дополнительно проверить и визуализировать это, построив входные данные по оси x и количество шагов по оси y, как показано ниже:
В приведенном выше сценарии вы можете ясно видеть, что, однако, вывод является линейным и выглядит следующим образом:
Квадратичная сложность (O(n^2))
Сложность алгоритма называется квадратичной, когда шаги, необходимые для выполнения алгоритма, являются квадратичной функцией количества элементов на входе. Квадратичная сложность обозначается как O(n^2). Взгляните на следующий пример, чтобы увидеть функцию с квадратичной сложностью:
В приведенном выше сценарии вы можете видеть, что у нас есть внешний цикл, который повторяет все элементы во входном списке, а затем вложенный внутренний цикл, который снова повторяет все элементы во входном списке. Общее количество шагов, выполненных в * n, где n-количество элементов во входном массиве.
На следующем графике показано количество входов и шагов для алгоритма с квадратичной сложностью.
Нахождение сложности сложных функций
В предыдущих примерах мы видели, что на входе выполняется только одна функция. Что делать, если на входе выполняется несколько функций? Взгляните на следующий пример.
Давайте разберем ваш сценарий на отдельные части. В первой части мы имеем:
Сложность этой части равна O(5). Поскольку в этом фрагменте кода выполняются пять постоянных шагов независимо от входных данных.
Мы знаем, что сложность приведенного выше фрагмента кода равна O(n).
Аналогично, сложность следующего фрагмента кода также O(n)
Наконец, в следующем фрагменте кода строка печатается три раза, следовательно, сложность равна O(3)
Чтобы найти общую сложность, мы просто должны добавить эти индивидуальные сложности. Давайте так и сделаем:
Упрощая вышеизложенное, мы получаем:
Ранее мы говорили, что когда вход (который в данном случае имеет длину n) становится чрезвычайно большим, константы становятся незначительными, то есть дважды или половина бесконечности все еще остается бесконечностью. Поэтому мы можем игнорировать константы. Конечная сложность алгоритма будет равна O(n).
Сложность худшего и Лучшего случая
Обычно, когда кто-то спрашивает вас о сложности алгоритма, он спрашивает вас о сложности наихудшего случая. Чтобы понять, каков наилучший и худший вариант сложности, посмотрите на следующий сценарий:
В приведенном выше сценарии у нас есть функция, которая принимает число и список чисел в качестве входных данных. Он возвращает true, если переданное число найдено в списке чисел, в противном случае он возвращает false. Если вы ищете 2 в списке, он будет найден в первом сравнении. Это наилучший случай сложности алгоритма, когда искомый элемент находится в первом искомом индексе. В лучшем случае сложность в этом случае равна O(1). С другой стороны, если вы ищете 10, он будет найден в последнем поисковом индексе. Алгоритм должен будет искать все элементы в списке, поэтому наихудшая сложность становится O(n).
В дополнение к сложности наилучшего и наихудшего случая вы также можете вычислить среднюю сложность алгоритма, которая говорит вам: “Учитывая случайный вход, какова ожидаемая временная сложность алгоритма”?
Сложность пространства
В дополнение к временной сложности, где вы подсчитываете количество шагов, необходимых для завершения выполнения алгоритма, вы также можете найти пространственную сложность, которая относится к количеству пробелов, которые вам нужно выделить в пространстве памяти во время выполнения программы.
Взгляните на следующий пример:
В приведенном выше скрипте функция принимает список целых чисел и возвращает список с соответствующими квадратами целых чисел. Алгоритм должен выделить память для того же количества элементов, что и во входном списке. Поэтому пространственная сложность алгоритма становится O(n).
Вывод
Обозначение Big-O-это стандартная метрика, используемая для измерения сложности алгоритма. В этой статье мы изучили, что такое нотация Big-O и как ее можно использовать для измерения сложности различных алгоритмов. Мы также изучали различные типы функций Big-O с помощью различных примеров Python. Наконец, мы кратко рассмотрели наихудшую и наилучшую сложность случая вместе с пространственной сложностью.
Сколько стоят операции над list, set и dict в Python? Разбираемся с временной сложностью
Автор перевода Иван Капцов
Программисту, работающему с данными, крайне важно выбирать правильные структуры данных для решения поставленной задачи, ведь выбор неправильного типа данных плохо влияет на производительность приложения. В этой статье объясняется нотация «О» большое и сложность ключевых операций структур данных в CPython.
Что означает нотация «O» большое?
В алгоритме выполняется ряд операций. Эти операции могут включать в себя итерацию по коллекции, копирование элемента или всей коллекции, добавление элемента в коллекцию, вставку элемента в начало или конец коллекции, удаление элемента или обновление элемента в коллекции.
«O» большое служит обозначением временной сложности операций алгоритма. Она показывает, сколько времени потребуется алгоритму для вычисления требуемой операции. Можно также измерить пространственную сложность (сколько места занимает алгоритм), но в этой статье мы сосредоточимся на временной.
Проще говоря, нотация «O» большое — это способ измерения производительности операции на основе размера ввода, известного как n.
Значения нотации «О» большое
На письме временная сложность алгоритма обозначается как O(n), где n — размер входной коллекции.
Обозначение константной временной сложности. Независимо от размера коллекции, время, необходимое для выполнения операции, константно. Это обозначение константной временной сложности. Эти операции выполняются настолько быстро, насколько возможно. Например, операции, которые проверяют, есть ли внутри коллекции элементы, имеют сложность O(1).
O(log n)
Обозначение логарифмической временной сложности. В этом случае когда размер коллекции увеличивается, время, необходимое для выполнения операции, логарифмически увеличивается. Эту сложность имеют потенциально оптимизированные алгоритмы поиска.
Обозначение линейной временной сложности. Время, необходимое для выполнения операции, прямо и линейно пропорционально количеству элементов в коллекции. Это обозначение линейной временной сложности. Это что-то среднее с точки зрения производительности. Например, если мы хотим суммировать все элементы в коллекции, нужно будет выполнить итерацию по коллекции. Следовательно, итерация коллекции является операцией O(n).
O(n log n)
Обозначение квазилинейной временной сложности. Скорость выполнения операции является квазилинейной функцией числа элементов в коллекции. Временная сложность оптимизированного алгоритма сортировки обычно равна O(n log n).
Обозначение квадратичной временной сложности. Время, необходимое для выполнения операции, пропорционально квадрату элементов в коллекции.
Обозначение факториальной временной сложности. Каждая операция требует вычисления всех перестановок коллекции, следовательно требуемое время выполнения операции является факториалом размера входной коллекции. Это очень медленно.
Нотация «O» большое относительна. Она не зависит от машины, игнорирует константы и понятна широкой аудитории, включая математиков, технологов, специалистов по данным и т. д.
Благоприятные, средние и худшие случаи
При вычислении временной сложности операции можно получить сложность на основе благоприятного, среднего или худшего случая.
Благоприятный случай. Как следует из названия, это сценарий, когда структуры данных и элементы в коллекции вместе с параметрами находятся в оптимальном состоянии. Например, мы хотим найти элемент в коллекции. Если этот элемент оказывается первым элементом коллекции, то это лучший сценарий для операции.
Средний случай. Определяем сложность на основе распределения значений входных данных.
Худший случай. Структуры данных и элементы в коллекции вместе с параметрами находятся в наиболее неоптимальном состоянии. Например, худший случай для операции, которой требуется найти элемент в большой коллекции в виде списка — когда искомый элемент находится в самом конце, а алгоритм перебирает коллекцию с самого начала.
Коллекции Python и их временная сложность
Список (list)
Список является одной из самых важных структур данных в Python. Можно использовать списки для создания стека или очереди. Списки — это упорядоченные и изменяемые коллекции, которые можно обновлять по желанию.
Операции списка и их временная сложность
Вставка: O(n).
Получение элемента: O(1).
Удаление элемента: O(n).
Проход: O(n).
Получение длины: O(1).
Множество (set)
Множества также являются одними из наиболее используемых типов данных в Python. Множество представляет собой неупорядоченную коллекцию. Множество не допускает дублирования, и, следовательно, каждый элемент в множестве уникален. Множество поддерживает множество математических операций, таких как объединение, разность, пересечение и так далее.
Операции с множествами и их временная сложность
Словарь (dict)
Словарь — это коллекция пар ключ-значение. Ключи в словаре уникальны, чтобы предотвратить коллизию элементов. Это чрезвычайно полезная структура данных.
Словари индексируются по ключам, которые могут быть строками, числами или даже кортежами со строками, числами или кортежами. Над словарём можно выполнить ряд операций, таких как сохранение значения для ключа, извлечение элемента на основе ключа, или итерация по элементам и так далее.
Операции со словарями и их временная сложность
Здесь мы считаем, что ключ используется для получения, установки или удаления элемента.
Получение элемента: O(1).
Установка элемента: O(1).
Удаление элемента: O(1).
Проход по словарю: O(n).
6.1. Теория¶
Во время своей работы программы используют различные структуры данных и алгоритмы, в связи с чем обладают разной эффективностью и скоростью решения задачи. Дать оценку оптимальности решения, реализованного в программе, поможет понятие вычислительной сложности алгоритмов.
6.1.1. Основные понятия¶
Вычислительная сложность пытается ответить на центральный вопрос разработки алгоритмов: как изменится время исполнения и объем занятой памяти в зависимости от размера входных данных?. С помощью вычислительной сложности также появляется возможность классификации алгоритмов согласно их производительности.
В качестве показателей вычислительной сложности алгоритма выступают:
Временная сложность (время выполнения).
Временная сложность алгоритма зачастую может быть определена точно, однако в большинстве случаев искать точное ее значение бессмысленно, т.к. работа алгоритма зависит от ряда факторов, например, скорости процессора, набора его инструкций и т.д.
Асимптотическая сложность оценивает сложность работы алгоритма с использованием асимптотического анализа.
Алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных.
6.1.2. Асимптотические нотации¶
Асимптотическая сложность алгоритма описывается соответствующей нотацией:
О-нотация, \(O\) («О»-большое): описывает верхнюю границу времени (время выполнения «не более, чем…»);
Омега-нотация, \(\Omega\) («Омега»-большое): описывает нижнюю границу времени (время выполнения «не менее, чем…»).
говорит о том, что алгоритм имеет квадратичное время выполнения относительно размера входных данных в качестве верхней оценки («О большое от эн квадрат»).
Каждая оценка при этом может быть:
наилучшая: минимальная временная оценка;
наихудшая: максимальная временная оценка;
средняя: средняя временная оценка.
При оценке, как правило, указывается наихудшая оценка.
Допустим, имеется задача поиска элемента в массиве. При полном переборе слева направо:
Наиболее часто используемой оценкой сложности алгоритма является верхняя (наихудшая) оценка, которая обычно выражается с использованием нотации O-большое.
Время выполнения не зависит от количества элементов во входном наборе данных.
Пример: операции присваивания, сложения, взятия элемента списка по индексу и др.
Время выполнения пропорционально количеству элементов в коллекции.
Пример: найти имя в телефонной книге простым перелистыванием, почистить ковер пылесосом и т.д.
Время выполнения пропорционально логарифму от количества элементов в коллекции.
Пример: найти имя в телефонной книге (используя двоичный поиск).
Время выполнения больше чем, линейное, но меньше квадратичного.
Пример: обработка \(N\) телефонных справочников двоичным поиском.
Время выполнения пропорционально квадрату количества элементов в коллекции.
Пример: вложенные циклы (сортировка, перебор делителей и т.д.).
6.1.3. Оценка сложности алгоритмов¶
Для оценки вычислительной сложности алгоритмов необходимо знать и учитывать сложности:
используемых структур данных;
совокупности различных операций.
6.1.3.1. Операции над структурами данных¶
В Python имеются коллекции (структуры данных), операции над которыми имеют определенную сложность.
6.1.3.1.1. Список и кортеж¶
Большинство операций со списком/кортежем имеют сложность \(O(N)\) (Таблица 6.1.1).
Сложность алгоритмов: О, о, Ω, Θ
В этой статье мы обсудим с Вами:
Помимо этого, мы рассмотрим сложность основных операций (if, for) и на примере Python-функции посчитаем сложность небольшого алгоритма.
Если Вы хотите получать еще больше интересных материалов по программированию, Data Science и математике, то подписывайтесь на нашу группу ВК, канал в Телеграме и Инстаграм. Каждый день мы публикуем полезный контент и вопросы с реальных собеседований.
О большое, O малое, Омега и Тета
Существует 4 нотации для описания поведения функций относительно друг друга. Давайте разберемся с каждой из них.
Формальные математические определения этих нотаций следующие:
Теперь стало понятнее, что означают записи f(x) = O(g(x)) и f(x) = о(g(x)). Конечно, эти определения еще осмыслить нужно, но хотя бы термины «доминирует» и «растет не быстрее» дают надежду на понимание 🙂
Однако теперь в игру вступают еще две нотации: Омега и Тета.
Посмотрим на графиках, как ведут себя функции.
На первом графике мы наблюдаем, что с увеличением значения n функция f(n) растет медленней cg(n). То есть функция f(n) ограничена сверху функцией cg(n), а значит f = O(g).
На третьем графика функция f(n) зажата между c1g(n) и c2g(n), то есть ограничена и сверху и снизу. Это и есть иллюстрация тетта-нотации.
Сложность алгоритмов
Пример: если мы увеличим количество входных данных (допустим, размер массива) в 10 раз, во сколько раз вырастет количество операций? В 10? В 100? А может в 2 или 20? Именно такую оценку и позволяет дать описание сложности алгоритма.
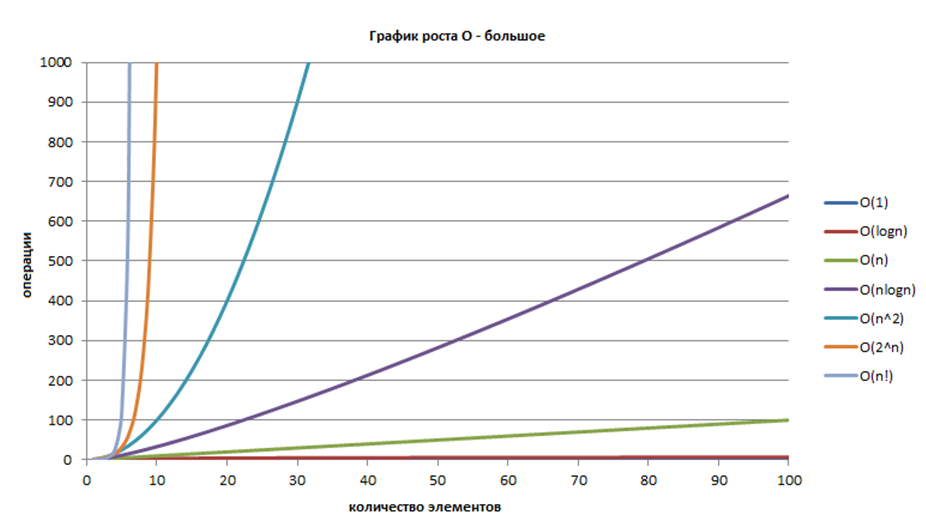
Для начала посмотрим на сложность, описываемую разными функциями.
На диаграмме цветом выделены классы сложности.
1. O(1) имеет наименьшую сложность
Алгоритм с таким классом сложности не зависит от размера входных данных. Если вы можете создать алгоритм для решения проблемы с O(1), то это будет наилучший выбор. Такую сложность имеет, например, операция вставки элемента в односвязный список.
2. O(log(n)) является более сложным, чем O(1), но менее сложным, чем полиномы
3. Сложность многочленов увеличивается с ростом степени
Например, алгоритмы со сложностью O(n^6) являются более сложными, чем O(n^2). Примером алгоритма с квадратичной сложностью служит алгоритм сортировки вставками, т.к. он подразумевает 2 вложенных цикла.
4. Показательные функции имеют большую сложность, чем полиномы.
5. Факториалы имеют самую большую сложность
Факториальная временная сложность — это когда количество вычислений в алгоритме прирастает факториально в зависимости от размера набора данных. Примером может служить рекурсивная функция расчета факториала.
Разобравшись со сложностью отдельных операций мы переходим к их комбинированию, потому что без этого более-менее сложный алгоритм мы оценить не сможем.
Закон сложения для O-нотации
При сложении двух классов сложности складываются функции этих классов. Однако, O(f(n) + g(n)) приводит нас к большему из двух исходных классов – так как меньший член выражения просто отбрасывается.
так как N растет быстрее, чем log N.
Это правило позволяет вычислить класс сложности для последовательности операций. Например, сначала мы выполняем выражение со сложностью O(f(n)), а следом за ним – O(g(n)). Тогда выполнение обоих выражений (одно за другим) будет иметь сложность O(f(n)) + O(g(n)), то есть O(f(n) + g(n)).
Пример
Вызов функции fun1(. ) имеет сложность O(N), а вызов fun2(. ) – O (N * log N). Вызываем эти функции друг за другом.
Сложность этого действия будет равна:
Если мы вызовем функцию fun1(. ) дважды, то получим:
Константа 2 в вычислениях отбрасывается.
Условия
Отдельно разберем выполнение условий (if). Сначала выполняется само условие, а затем один из блоков (if или else).
Предположим, что вычисление условия test имеет сложность O(T), блока block 1 – O(B1), а блока block 2 – O(B2).
Тогда сложность всего кода будет равна:
Подставим реальные значения:
и вычислим сложность кода:
Если бы операция test имела класс сложности O(N^3), то общая сложность кода составила бы O(N^3).
В O-нотации мы всегда отбрасываем менее значимые элементы.
Закон умножения для O-нотации
Если мы повторяем N раз некоторый процесс с классом сложности O(f(N)), то результирующий класс сложности будет равен:
Предположим, некоторая функция f(. ) имеет класс сложности O(N^2). Выполним ее в цикле N раз:
Сложность этого кода будет равна:
Это правило позволяет вычислять класс сложности для выполнения некоторого повторяющегося несколько раз выражения. Необходимо умножить количество повторений на класс сложности самого выражения.
Расчет сложности алгоритмов на Python
Давайте посчитаем сложность на примере простого алгоритма на языке Python, чтобы лучше понимать процесс вычисления.
Возьмем код, который определяет, состоит ли список из уникальных значений (т.е. нет ли в нем дубликатов). Размер списка обозначим как N, а сложность операции сравнения элементов примем за O(1).
Список уникален, если каждое его значение не встречается ни разу «справа» от элемента. Для значения alist[i] «правым» фрагментом списка будет срез alist[i+1:].
Определим сложность для каждой строки функции:
Таким образом, полная сложность цикла (по ранее рассмотренному нами правилу) равна:
Если размер списка увеличится вдвое, то выполнение функции займет в 4 раза больше времени.
Эпилог
Итак, давайте подведем итог, что же мы узнали:
Основные правила расчета сложности алгоритмов:
Сложность блока if рассчитывается так: условие выполняется всегда, а затем один из блоков. Для расчета максимальной сложности предполагаем, что выполняется самый сложный блок:
Сложность блока for рассчитывается просто: количество индексов умножается на сложность вычисления индекса и на сложность самой функции в цикле.
Вот мы и разобрали с Вами основные положения расчета сложности алгоритмов. При этом теперь Вы будете не просто правильно определять сложность, а понимать математическую основу этого процесса.
Если Вы хотите получать еще больше интересных материалов по программированию, Data Science и математике, то подписывайтесь на нашу группу ВК, канал в Телеграме и Инстаграм. Каждый день мы публикуем полезный контент и вопросы с реальных собеседований.