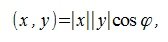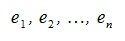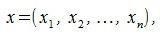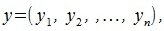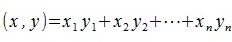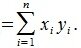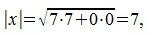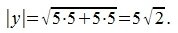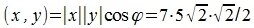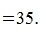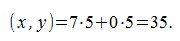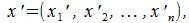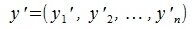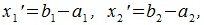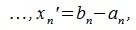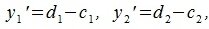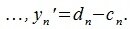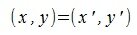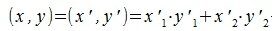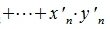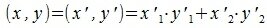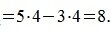Как посчитать скалярное произведение векторов
Обозначим через 
угол между векторами 
Тогда
Возведя эти равенства в квадрат и сложив, мы получим следующее тождество:
Но квадрат модуля вектора равеп скалярному квадрату этого вектора. Поэтому
в силу чего предыдущее тождество принимает такой вид:
Это тождество мы и будем называть о с 
Его полезно сформулировать так: сумма квадратов скалярного и векторного произведений двух векторов равна произведению квадратов этих векторов.
2. Формула, выражающая векторно-скалярное произведение через попарные скалярные произведения сомножителей.
Квадрат векторно-скалярного произведения трех векторов, т. е.
можно рассматривать как квадрат скалярного произведения двух векторов: 
.
Согласно основному тождеству (4.32) квадрат скалярного произведения двух векторов равен произведению квадратов этих векторов минус квадрат их векторного произведения. Поэтому
Квадрат векторного произведения 
мы пайдем, пользуясь основным тождеством (4.32):
Для вычисления квадрата векторно-векторного произведения 
воспользуемся формулой разложения (4.11) этого произведения:
Подставив все это в выражение для квадрата векторно-скалярного произведения (4.33), мы получим
Эта формула и является по существу искомой. Мы только приведем ее к более удобному для запоминания виду.
Для этого перегруппируем члены так:
Нетрудно видеть, что правая часть представляет собой развернутый определитель третьего порядка. Окончательно формула принимает такой вид:
Как мы увидим, эта замечательная формула вместе с формулой разложения векторно-векторного произведения в известном смысле замыкает всю векторную алгебру, позволяя все вычисления сводить к вычислениям лишь скалярных произведений.
Скалярное произведение векторов
Скалярным произведением ненулевых векторов x и y называется произведение
Если x=0 или y=0, то скалярное произведение равно нулю.
Пусть в n-мерном пространстве задан ортонормированный базис
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пусть заданы векторы
тогда скалярное произведение (x,y) векторов x и y определяется соотношением:
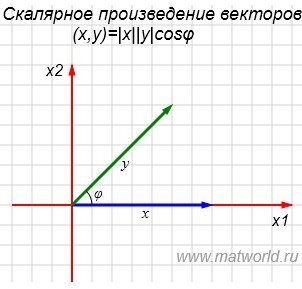
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,0) и y=(5,5).
Для вычисления скалярного произведения методом (1), вычислим нормы векторов x и y:
Учитывая что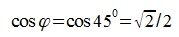 
, получим:
Теперь вычислим скалярное произведение векторов x и y используя выражение (2):
Получили одинаковые результаты, но посдедний вариант вычисления проще и не требует знания угла между векторами.
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x= AB и y= CD, где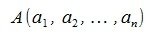 
,
,
,
.
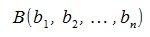
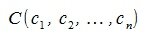
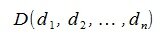
Переместим векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
Учитывая (2) получаем:
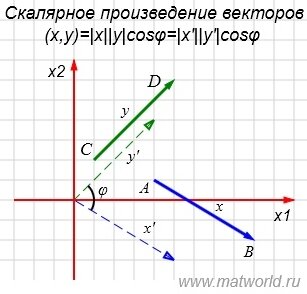
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x= AB и y= CD, где A(4,1), B(9,-2), C(1,2), D(5,6).
Как посчитать скалярное произведение векторов
Обозначим через угол между векторами Тогда
Возведя эти равенства в квадрат и сложив, мы получим следующее тождество:
Но квадрат модуля вектора равеп скалярному квадрату этого вектора. Поэтому
в силу чего предыдущее тождество принимает такой вид:
Это тождество мы и будем называть о с Его полезно сформулировать так: сумма квадратов скалярного и векторного произведений двух векторов равна произведению квадратов этих векторов.
2. Формула, выражающая векторно-скалярное произведение через попарные скалярные произведения сомножителей.
Квадрат векторно-скалярного произведения трех векторов, т. е.
можно рассматривать как квадрат скалярного произведения двух векторов: .
Согласно основному тождеству (4.32) квадрат скалярного произведения двух векторов равен произведению квадратов этих векторов минус квадрат их векторного произведения. Поэтому
Квадрат векторного произведения мы пайдем, пользуясь основным тождеством (4.32):
Для вычисления квадрата векторно-векторного произведения воспользуемся формулой разложения (4.11) этого произведения:
Подставив все это в выражение для квадрата векторно-скалярного произведения (4.33), мы получим
Эта формула и является по существу искомой. Мы только приведем ее к более удобному для запоминания виду.
Для этого перегруппируем члены так:
Нетрудно видеть, что правая часть представляет собой развернутый определитель третьего порядка. Окончательно формула принимает такой вид:
Как мы увидим, эта замечательная формула вместе с формулой разложения векторно-векторного произведения в известном смысле замыкает всю векторную алгебру, позволяя все вычисления сводить к вычислениям лишь скалярных произведений.
Скалярное произведение векторов
Скалярным произведением ненулевых векторов x и y называется произведение
Если x=0 или y=0, то скалярное произведение равно нулю.
Пусть в n-мерном пространстве задан ортонормированный базис
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пусть заданы векторы
тогда скалярное произведение (x,y) векторов x и y определяется соотношением:
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,0) и y=(5,5).
Для вычисления скалярного произведения методом (1), вычислим нормы векторов x и y:
Учитывая что 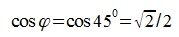, получим:
Теперь вычислим скалярное произведение векторов x и y используя выражение (2):
Получили одинаковые результаты, но посдедний вариант вычисления проще и не требует знания угла между векторами.
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x= AB и y= CD, где ,,,.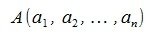
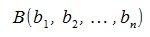
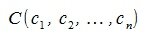
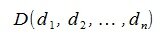
Переместим векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
Учитывая (2) получаем:
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x= AB и y= CD, где A(4,1), B(9,-2), C(1,2), D(5,6).
Скалярное произведение векторов
Содержание
Определение [ править ]
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Если один из векторов нулевой, то угол не определен, и произведение считают равным нулю.
Свойства скалярного произведения:
Геометрический смысл скалярного произведения [ править ]
Связь с проекциями [ править ]
Таким образом, скалярное произведение
Связь с длинами [ править ]
Рассмотрим скалярное произведение вектора на самого себя.
Связь с углами [ править ]
Рассмотрим скалярное произведение единичных векторов. Поскольку их длины равны 1, то
Скалярное произведение в ортонормированной системе координат [ править ]
a ⋅ b = ( a 1 e 1 + a 2 e 2 + a 3 e 3 ) ⋅ ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) = = a 1 b 1 e 1 ⋅ e 1 + a 2 b 2 e 2 ⋅ e 2 + a 3 b 3 e 3 ⋅ e 3 + ( a 1 b 2 + a 2 b 1 ) e 1 ⋅ e 2 + ( a 1 b 3 + a 3 b 1 ) e 1 ⋅ e 3 + ( a 2 b 3 + a 3 b 2 ) e 2 ⋅ e 3 <\displaystyle <\begin |
Аксиоматический подход [ править ]
При аксиоматическом подходе скалярное произведение определяется как некоторая функция, аргументы которой — два вектора, результат — число, не зависящее от системы координат, обладающее свойствами:
Тогда производными понятиями становятся