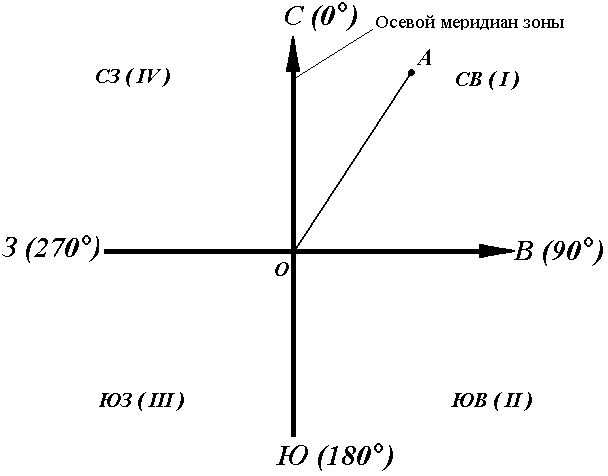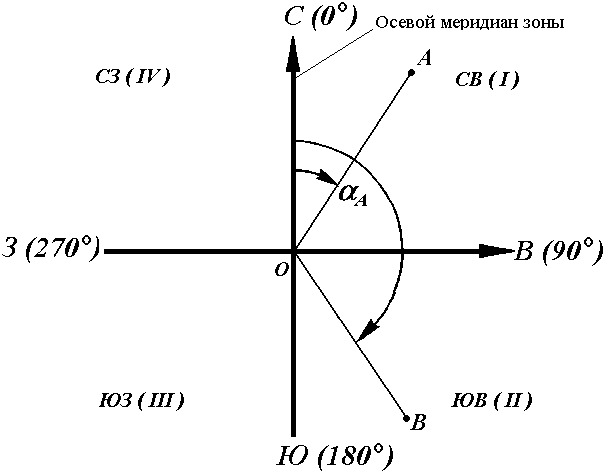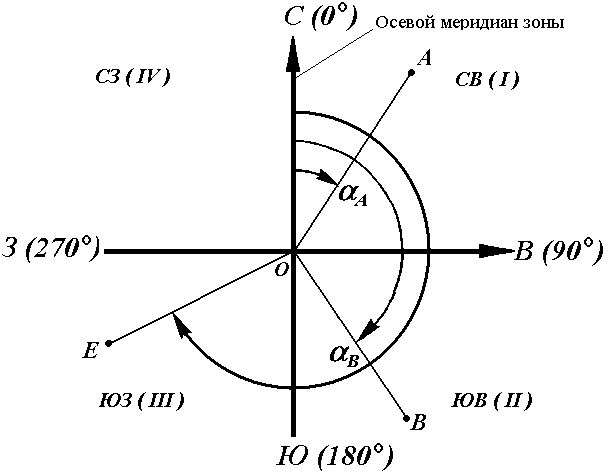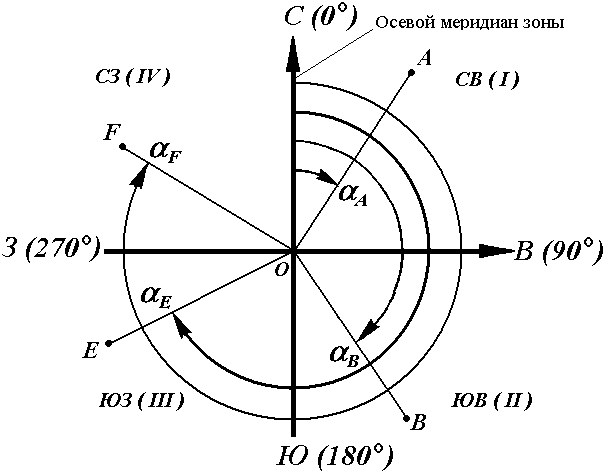Как посчитать румб в геодезии
Дирекционные углы и осевые румбы



Лекция 6
Ориентирование линии. Прямая и обратная геодезические задачи.
При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием.
Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света.
В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута.
Дирекционные углы и осевые румбы
Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16).
Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.
Рис. 16. Дирекционные углы
Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.
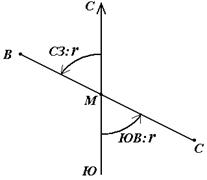
В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим αBC является прямым дирекционным углом линии ВС в точке М, а угол αCB – обратным дирекционным углом этой же линии в той же точке.
Рис. 17. Прямое и обратное направление линии
Из рисунка видно, что αCB = αBC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.
Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18).
Осевым румбомназывается острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.
Рис. 18. Румбы и дирекционные углы
Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).
Зависимость между дирекционными углами и румбамиопределяется для четвертей по следующим формулам:
I четверть (СВ) r = α
II четверть (ЮВ) r = 180° – α
III четверть (ЮЗ) r = α – 180°
IV четверть (СЗ) r = 360° – α
Ориентирные углы: дирекционные, азимуты, румбы и их связь
Содержание:
| Предмет: | Геодезия |
| Тип работы: | Курсовая работа |
| Язык: | Русский |
| Дата добавления: | 05.03.2019 |
Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!
По этой ссылке вы сможете найти много готовых курсовых работ по геодезии:
Посмотрите похожие темы возможно они вам могут быть полезны:
Введение:
Азимуты и румбы геометрически связаны, так что азимуты могут быть использованы для простого определения румб, и наоборот, азимуты могут быть рассчитаны по румбам. Из рисунка хорошо видно, что для линий, имеющих направления.
Из этого рисунка можно сделать очень важный вывод о том, что угол, составленный по направлениям в любой точке, равен разности азимутов ее сторон.
Связь между азимутами и румбами
При выполнении геодезических работ на земле, работе с картой или чертежом необходимо определить положение линии (ориентировать линию) относительно стран мира или какое-либо направление, принятое в качестве исходного.
Ориентация заключается в том, что они определяют угол между исходным направлением и направлением этой линии. Для начального направления ориентации возьмите истинный (географический) магнитный меридиан или ось абсцисс прямоугольной системы координат плана. Углами, которые определяют направление линии, являются истинный и магнитный азимуты, угол направления и румба.
В геодезии принято различать прямое и обратное направления линии. Если направление линии MN из точки M в точку N считается прямым, то NM является противоположным направлением той же линии. В соответствии с этим угол A является прямым азимутом линии MN в точке M, а A1 является обратным азимутом той же линии в точке N.
Меридианы разных точек не параллельны друг другу, так как они сходятся в точках полюсов. Следовательно, азимут линии в разных точках имеет разное значение. Угол между направлениями двух меридианов называется приближением меридианов и обозначается через γ. Соотношение между прямым и обратным азимутами линии MN выражается формулой A1 = A + 180 ° + γ.
Иногда для ориентации линии местности используют не азимуты, а румбу.
Угол направления любого направления не измеряется непосредственно на земле, его значение можно рассчитать, если для этого направления определен истинный азимут. Дана взаимосвязь между направленным углом a и истинным азимутом A.
Направленные углы обозначаются и рассчитываются так же, как истинные азимуты; они только считают абсциссу с северного и южного направлений.
Склонение магнитной стрелки не остается постоянным даже в данной точке Земли (различаются вековые, годовые и суточные изменения склонения). Больше всего страдают дневные колебания, колебания достигают 15 ’. Следовательно, магнитная стрелка приблизительно указывает положение магнитного меридиана, и вы можете ориентировать линии местности по магнитным азимутам, когда высокая точность не требуется.
Истинные азимуты и румба
В дополнение к осевому меридиану зоны, при ориентировании линий области, направление истинного (географического) меридиана может быть взято в качестве основного направления.
Положение линии местности относительно истинного меридиана определяется истинным азимутом или истинной румбой.
Истинный азимут A измеряется от 0 ° до 360 °. Соотношение между истинными азимутами и ревами такое же, как между направленными углами и осевыми ревенями.
Истинные меридианы, проходящие через точки Земли с разными долготами, не параллельны друг другу и сходятся на полюсах. Поэтому азимуты одной и той же прямой, определяемой относительно разных истинных меридианов, отличаются на γ, который называется углом сближения меридианов.
Чтобы перейти от угла направления к истинному азимуту и наоборот, необходимо знать угол захода γ между осевым и истинным меридианом. Соотношение между истинным азимутом и направленным углом следующее.
Магнитные азимуты и румбы
При ориентировании линий местности направление магнитного меридиана также может быть принято в качестве основного направления.
Магнитная стрелка на концах имеет точки, в которых сосредоточены магнитные массы. Линия, соединяющая их, называется магнитной осью стрелки.
Вертикальная плоскость, проходящая через магнитную ось стрелки, является плоскостью магнитного меридиана.
Линия пересечения плоскости магнитного меридиана с горизонтальной плоскостью дает направление магнитного меридиана.
Горизонтальный угол, измеренный от северного направления магнитного меридиана по часовой стрелке до этой линии, называется магнитным азимутом Am.
Магнитное склонение в разных точках Земли различно и противоречиво. Различают светские, годовые и дневные изменения склонения. В связи с этим магнитная стрелка приблизительно указывает направление магнитного меридиана, и линия может быть ориентирована вдоль него только тогда, когда большая точность ориентации не требуется.
Азимуты, румбы, направленные углы и зависимости между ними
При выполнении геодезических работ на земле, работе с картой или чертежом необходимо определить положение линии (ориентировать линию) относительно стран мира или какое-либо направление, принятое в качестве исходного.
В геодезии принято различать прямое и обратное направления линии. Если направление линии MN из точки M в точку N считается прямым, то NM является противоположным направлением той же линии. В соответствии с этим угол A1 является прямым азимутом линии MN в точке M, а A2 является обратным азимутом той же линии в точке N.
Меридианы разных точек не параллельны друг другу, так как они сходятся в точках полюсов. Следовательно, азимут линии в разных точках имеет разное значение.
Угол между направлениями двух меридианов называется приближением меридианов и обозначается через γ. Соотношение между прямым и обратным азимутами линии MN выражается следующей формулой: A2 = At + 1800 + γ.
Иногда для ориентации линии местности используют не азимуты, а румбу.
Направление магнитной оси свободно подвешенной магнитной иглы называется магнитным меридианом. Угол между северным направлением магнитного меридиана и направлением этой линии называется магнитным азимутом. Магнитный азимут, как и истина, считается по часовой стрелке; оно также колеблется от 0 до 360 °. Соотношение между магнитными азимутами и магнитными кольцами такое же, как между истинными кольцами. Поскольку магнитный полюс не совпадает с географическим, направление магнитного меридиана в данной точке не совпадает с направлением истинного меридиана. Горизонтальный угол между этими направлениями называется склонением магнитной стрелки 5. В зависимости от того, в каком направлении северный конец стрелки отклоняется от направления истинного меридиана, различаются восточное и западное склонения.
В разных точках Земли магнитная стрелка имеет разное склонение. Так, на территории Российской Федерации она колеблется в пределах (0 ± 15) °.
Склонение магнитной стрелки не остается постоянным даже в данной точке Земли (различаются вековые, годовые и суточные изменения склонения). Больше всего меняется суточное склонение, колебания которого достигают 15 ‘. Поэтому магнитная стрелка приблизительно указывает положение магнитного меридиана, и вы можете ориентировать линии местности по магнитным азимутам, когда высокая точность не требуется.
Вывод:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Как посчитать румб в геодезии
Смотреть что такое «румб» в других словарях:
РУМБ — (англ. rhumb). 1) одно из 32 направлений компаса, подразделяемых еще на половины и четверти. 2) часть горизонта = 11,25 град. или 1/32 окружности. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. РУМБ 1) 1/32… … Словарь иностранных слов русского языка
румб — а; м. [англ. rhumb] Мор. 1. Деление на круге компаса, соответствующее 1/32 части горизонта, для определения положения корабля по отношению к странам света. 2. Направление к точкам горизонта относительно стран света; угол между двумя такими… … Энциклопедический словарь
РУМБ — (Point of compass) постоянное и вполне определенное в данном месте земли положение истинного меридиана, определяющего направление истинного N S и ему перпендикулярное направление О W, позволяет мореплавателю точно ориентировать относительно этих… … Морской словарь
румб — компасный румб Буквенное обозначение направления, указанного на картушках компаса, допускаемое, но не обязательное. На полной окружности имеется 32 румба, которые одинаково удалены один от другого на картушке, в результате чего дуга между двумя… … Справочник технического переводчика
РУМБ — РУМБ, румба, муж. (от греч. rhymbos круг, круговое движение) (мор.). Каждое из 32 делений на круге компаса, соответствующее каждой 1/32 части горизонта. Держать курс по такому то румбу. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
РУМБ — РУМБ, а, муж. (спец.). 1. Направление к точкам видимого горизонта относительно стран света или угол между двумя такими направлениями. 2. Деление на круге компаса, соответствующее 1/32 части окружности горизонта. | прил. румбовый, ая, ое. Толковый … Толковый словарь Ожегова
румб — угол, штрих Словарь русских синонимов. румб сущ., кол во синонимов: 2 • угол (27) • штрих (21) … Словарь синонимов
румб — румб, а (деление на круге компаса) … Русское словесное ударение
Румб — м. 1. Мера угла окружности горизонта, разделённой на 32 части. отт. Деление на круге компаса, соответствующее 1/32 части видимого горизонта (в морской навигации). 2. Направление к точкам видимого горизонта относительно стран света (от… … Современный толковый словарь русского языка Ефремовой
Определение дирекционных углов и румбов сторон полигона



Для определения дирекционного угла каждой из сторон теодолитного хода необходимо знать исходный дирекционный угол одной из сторон. Этот угол получают путем привязки данной стороны к пункту геодезической опорной сети или определением для этой стороны истинного или магнитного азимута. По известному дирекционному углу и по откорректированным после расчетов невязок значениям углов полигона вычисляют дирекционные углы всех сторон по формулам:
Последняя строка в системе равенств – контрольная. Она как бы замыкает выполненные расчеты и показывает, что в замкнутом полигоне сумма измеренных и рассчитанных углов удовлетворяет соответствующим условиям.
а – замкнутого; б – диагонального.
Прямая и обратная задача геодезии
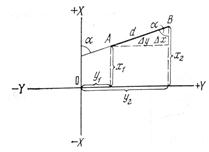
Прямая задача: даны координаты X1 и Y1 точки А начала линии АВ и дирекционный угол α. Требуется определить координаты X2 и Y2 точки В.
Из рисунка следует, что координаты точки В конца линии АВ:
Где ΔX; и ΔY есть приращения координат. Очевидно, что:
Обратная задача геодезии: даны координаты X1 и Y1 точки А начала линии АВ и координаты X2 и Y2 точки В – конца этой линии. Требуется определить дирекционный угол и длину этой линии.
Из рисунка следует, что:
или d = ΔX / cos r = ΔY / sin r;
 |
Вычисление координат вершин теодолитного хода. Невязки в приращениях координат замкнутого полигона вычисляются, исходя из факта равенства нулю суммы проекций полигона на координатную ось. То есть: ΣΔX = 0 и ΣΔY = 0. Вследствие ошибок измерений фактическая сумма приращений координат нулю оказывается не равной.
Тогда ΣΔX = fx и ΣΔY = fy называются, соответственно, невязками в приращениях координат по оси абсцисс и оси ординат. Перед распределением невязок по координатам необходимо определить их допустимость по формуле:
где невязка в периметре fp = 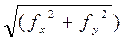
После исправления приращений координат определяют координаты всех вершин полигона по исходной координате первой точки, привязанной к опорной геодезической сети. Контролем вычисления координат является последовательное вычисление координат точек замкнутого полигона, чтобы в результате получить координаты исходной точки.
Таблица: Ведомость вычисления координат основного полигона
Решение задач по геодезии контрольной работы № 1 для студентов заочного отделения
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ЯРОСЛАВСКОЙ ОБЛАСТИ
ГОУ СПО ЯО РЫБИНСКИЙ ЛЕСХОЗ-ТЕХНИКУМ
зам. директора по учебной работе
_______________ __ Кируца Е.И.
«____» ___________ ____ 20 __ г.
«Решение задач по геодезии контрольной работы № 1 для студентов заочного отделения»
Основной целью методической разработки является оказание помощи студентам-заочникам в организации самостоятельной работы по изучению «Геодезии» в объёме действующей программы. Такая работа требует большого упорства и умения читать, понимать и применять прочитанное, но в то же время она способствует дальнейшему развитию умений и навыков самообразования.
Предназначена преподавателям геодезии.
Методическая работа рассмотрена на заседании цикловой комиссии общепрофессиональных дисциплин и рекомендована к использованию в учебном процессе.
Протокол № ____ от ___________
Составитель работы Кируца Петр Леонидович, преподаватель дисциплины «Геодезия».
Решение задач контрольной работы № 1…………………………………………….. стр. 5
Геодезия – это наука об измерениях на земной поверхности, проводимых для определения формы и размеров Земли, изображения её на планах, картах и профилях, которые используются при решении инженерных, экономических и других задач.
Эта наука возникла в глубокой древности и развивалась с ростом потребностей человека в жилье, делении земельных массивов на участки, строительстве каналов для осушения и орошения, строительстве различных населенных пунктов, изучении водного режима рек, морей и водных бассейнов, природных богатств страны, недр Земли и т. д.
Для успешного решения лесохозяйственных задач, кроме специальных знаний нужны и геодезические знания.
Проведение лесоустройства, восстановление границ землепользований, отвод площадей под различные виды пользования, строительство лесовозных и лесохозяйственных дорог, посадка лесных культур и лесных полос требуют от лесовода знаний и умения пользоваться планами и картами, выполнять геодезические расчёты и осуществлять перенос в натуру объектов лесохозяйственного пользования.
При изучении данной дисциплины студенты заочного отделения познакомятся с методами и принципами съемки, съемкой участков местности и другими видами геодезических работ.
КОНТРОЛЬНОЙ РАБОТЫ № 1.
Задача № 1. Вычисление расстояний.
Вычислить расстояние, абсолютную и относительную погрешности его измерения по данным, приведенным в таблице № 1.
Число шпилек в комплекте
Число шпилек у заднего мерщика, шт.
в прямом направлении
в обратном направлении
Расстояние, измеренное мерной лентой, вычисляется по формуле:
L = ((5)10р + n ) ℓ о + а, где:
р – число передач шпилек;
n – число шпилек в руках у заднего мерщика;
а – остаток или домер.
Ходовая линия измерена дважды, в прямом и обратном направлении.
L прямое = (5 · 3 + 2) · 20 + 3,26 = м,
L обратное. = (5 ∙ 3 + 20) ∙ 20 + 2,92 = м.
Для дальнейшего использования применяется среднеарифметическая длина ходовой линии
Для определения абсолютной и относительной погрешности необходимо обращаться к теме «Теория погрешностей».
Абсолютная погрешность указывается в одинаковых единицах измерения и вычисляется по формуле
Относительная погрешность указывает на точность выполнения измерительных работ, записывается в виде дроби
Относительная ошибка указывает на то, что на каждые 1248,8 метров, ошибка составляет 1 метр.
Задача № 2. Вычисление горизонтальных проложений.
По результатам измерения наклонной линии землемерной лентой и угла наклона эклиметром вычислить горизонтальное проложение этой линии.
Горизонтальное проложение определяется различными способами, самый простой по формуле
где L – длина линии,
Пример: угол наклона 5,5 о равен 5 о 30’. Для определения значения cos пользуемся таблицами Брадиса.
Горизонтальные проложения при составлении плана участка местности необходимо уменьшать в соответствии с масштабом. Численный масштаб принято изображать в виде дроби с числителем, равным единице, например: 1/1000. Приведённый масштаб означает, что длину линий местности при переносе на план надо уменьшить в 1000 раз, или по-другому: на план следует откладывать 1/1000 часть измеренной линии местности.
Удобнее пользоваться именованным масштабом. При этом надо иметь в виду, что в числителе указывают размер на чертеже (плане), а в знаменателе – соответствующий ему размер в натуре (на местности). Тогда можно сказать, что 1 см плана соответствует 1000 см = 10 м местности.
Начертим график линейного и поперечного масштабов.
М 1:5000 в 1 см – 50 м 365,33 м : 50 м/см = 7,31 см
При пользовании линейным графиком нередко возникает необходимость глазомерно определить доли наименьшего деления линейного масштаба, в результате чего появляются неизбежные погрешности. Чтобы избежать глазомерного определения десятых долей наименьшего деления масштаба и повысить точность построений и измерений расстояний на плане чаще применяют поперечный масштаб.
Для построения поперечного масштаба на горизонтальной прямой откладывают 5-7 раз основание масштаба, равное 2 см. Из концов отложенных отрезков восстанавливают к прямой перпендикуляры длиной по 2,5 см. Крайние из них делят на 10 равные частей и соответствующие точки соединяют прямыми, параллельными нижней линии масштаба. Затем первое слева основание и противолежащий равный ему отрезок на самой верхней горизонтальной линии делят также на 10 равных частей и точки этого деления соединяют наклонными линиями, т.е. трансверсалями.
Чтобы отложить в масштабе 1:5000 длину горизонтального проложения необходимо:
длину горизонтального проложения разделить на удвоенное основание масштаба
365,33 м:100 м = 3,653
По графику откладывают: 3 основания
6 делений влево от 0
3 части вверх от 5 линии к шестой на глаз.
Величина масштаба – расстояние на местности, соответствующее 1 см плана величина М 1:5000 – 50 метров.
Точность масштаба – расстояние на местности, соответствующее 0,1 мм на плане данного масштаба 1 : 5000 – 0,5 м.
Задача № 3. Ориентирование линий.
Зависимость между азимутом и румбом определяется по следующим формулам:
СВ 60 о 05’, А = 60 о 05’
II четверть А (90 о – 180 о ), румб во второй четверти называется ЮВ (юго-восточный)
А = 180 о – ЮВ 24 о 15’ = 155 о 45’
III четверть А (180 о – 270 о ), румб называется ЮЗ (юго-западный)
Пример: А = 211 о 25’
А = 180 о + ЮЗ 25 о 05’ = 205 о 05’
IV четверть А (270 о – 360 о ), румб называется СЗ (северо-западный)

Пример: А = 305 о 50’
А = 360 о – СЗ 82 о 20’ = 277 о 40’
Задача № 4. Составление плана буссольной съёмки по румбам.
Результаты измерений во время съёмки заносят в полевой журнал (таблица № 2) и дублируют их запись для надёжности и наглядности на схематическом чертеже – абрисе (рис 3), который выполняется в произвольном масштабе.