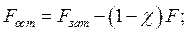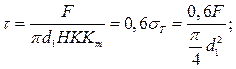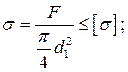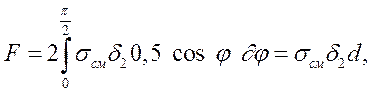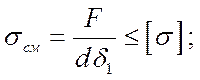Как посчитать резьбу на срез

Детали машин

Расчет резьбовых соединений на прочность

Критерии работоспособности резьбы и причины отказа

Для ответственных деталей используют легированные стали 40Х, 30ХГСА.
Для повышения коррозионной стойкости резьбовые детали оксидируют, омедняют, оцинковывают.

Причины выхода из строя резьбовых соединений

В зависимости от характера нагружения и способа сборки деталей резьбовых соединений их делят на соединения без предварительной затяжки и с предварительной затяжкой.
Основные критерии работоспособности резьбовых соединений определяют на основе анализа причин выхода из строя крепежных деталей.
Выход из строя (отказ) винтов, болтов, шпилек происходит вследствие:

Гайки чаще всего выходят из строя по причине смятия, среза или износа резьбы или разрушения (износа) боковых граней.

Разрушение болтов под головкой имеет место из-за наличия концентраторов напряжений в зоне перехода от стержня к головке. В стандартных крепежных изделиях этот недостаток устраняют с помощью галтелей (плавного перехода между сечениями), значительно уменьшающих концентрацию напряжений. По этой причине расчеты болтов на прочность по этому критерию, как правило, не производят.

В некоторых конструкциях (где крепежные детали нагружены поперечной силой) производят расчет стержней болтов, шпилек и винтов на срез и смятие.

Примеры расчетов резьбовых соединений для разных случаев крепления деталей и связанных с этим характером нагрузок приведены ниже.

Расчет одиночных болтов при постоянной нагрузке

Расчет незатянутого болта при действии осевой силы

откуда можно определить минимальный диаметр болта, способный выдержать допускаемое напряжение.
Проектировочный расчет для незатянутого резьбового соединения выполняют по формуле:

где: d₀ – минимальный расчетный диаметр болта; F – внешняя осевая (продольная) сила.

Расчет затянутого болта, нагруженного внешней растягивающей силой

Для обеспечения плотности стыка и жесткости соединения болты (винты, шпильки) затягивают. В затянутом резьбовом соединении полная нагрузка на болт составляет:

где: F₀ – сила предварительной затяжки; χ – коэффициент внешней нагрузки, учитывающий, какая часть внешней нагрузки при совместной деформации болта и деталей стыка приходится на болт;
χ = 0,2…0,3 – при соединении деталей без прокладки,
χ = 0,4…0,5 – при соединении деталей с упругой прокладкой (резина, картон и т. п.).

Затянутый болт растянут и скручен за счет трения в резьбе и под головкой болта.
Эквивалентное напряжение в стержне по гипотезе видоизменения определяется по формуле:

Расчет болтов для крепления крышек

Расчет на прочность болтов для крепления крышек цилиндров, находящихся после затяжки под давлением, может быть произведен по формуле, учитывающей полную нагрузку (с учетом кручения) на болт:

Расчетный диаметр болта определяют по формуле:

где: [σ_р] = σ_т / [s] ; σ_т – предел текучести материала; [s] – коэффициент запаса прочности, учитывающий условия работы соединения, материал и диаметр резьбы.
В начале расчета величина [s] задается ориентировочно, после расчета уточняется.

Расчет болта под действием поперечной силы

Условие прочности на срез определяется зависимостью:

Проверочный расчет на смятие осуществляется по формуле:

Расчет болта, установленного в отверстие с зазором и нагруженного поперечной силой, производится с учетом силы трения, препятствующей сдвигу деталей под действием внешней силы. Сила трения возникает из-за необходимой затяжки такого резьбового соединения. Затянутый болт работает на растяжение и скручен за счет трения в резьбе.

Потребная затяжка определяется по зависимостям:

Влияние скручивания болта при затяжке учитывают, увеличивая расчетную нагрузку на 30%:

Расчетный диаметр болта:

Формулы для проверочного расчета болтов

Проверочные формулы для болтов (шпилек, винтов) в зависимости от вида нагружения стержня:

Источник

Расчет крепежных резьбовых соединений

Основным критерием работоспособности крепежных резьбовых соединений является прочность. Стандартные крепежные детали сконструированы равнопрочными по следующим параметрам: по напряжениям среза и смятия в резьбе, напряжениям растяжения в нарезанной части стержня и в месте перехода стержня в головку. Поэтому для стандартных крепежных деталей в качестве главного критерия работоспособности принята прочность стержня на растяжение, и по ней ведут расчет болтов, винтов и шпилек. Расчет резьбы на прочность выполняют в качестве проверочного лишь для нестандартных деталей.

Расчет резьбы.Как показали исследования, проведенные Н.Е. Жуковским, силы взаимодействиямежду витками винта и гайки распределены в значительной степени неравномерно, однако действительный характер распределения нагрузки по виткам зависит от многих факторов, трудно поддающихся учету (неточности изготовления, степени износа резьбы, материала и конструкции гайки и болта и т.д.). Поэтому при расчете резьбы условно считают, что все витки нагружены одинаково, а неточность в расчете компенсируют значением допускаемого напряжения.

Условие прочности резьбы на срез имеет вид

где Q– осевая сила; A_ср– площадь среза витков нарезки; для винта (см. рис.1.9) A_ср= πd₁kH_г,для гайки А_ср = πDkH_г.Здесь Н_г – высота гайки; k– коэффициент, учитывающий ширину основания витков резьбы: для метрической резьбы для винта k≈ 0,75, для гайки k≈ 0,88; для трапецеидальной и упорной резьб (см. рис.1.11, 1.12) k≈ 0,65; для прямоугольной резьбы (см. рис.1.13) k= 0,5. Если винт и гайка из одного материала, то на срез проверяют только винт, так как d_l (δ₁ + δ₂), то в расчет (при одинаковом материале деталей) принимается меньшая величина. Обычно из условия прочности на срез определяют диаметр стержня болта, а затем проводят проверочный расчет на смятие.

Во втором варианте конструкции болтового соединения, нагруженного поперечной силой, диаметр стержня болта получается в два–три раза меньше, чем в первом варианте (без разгрузочных деталей).

Допускаемые напряжения.Обычно болты, винты и шпильки изготовляют из пластичных материалов, поэтому допускаемые напряжения при статической нагрузке определяют в зависимости от предела текучести материала, а именно:

при расчете на растяжение

при расчете на срез

при расчете на смятие

Рис. 2.8. Болтовое соединение без зазора

Значения допускаемого коэффициента запаса прочности [s] зависят от характера нагрузки (статическая или динамическая), качества монтажа соединения (контролируемая или неконтро­лируемая затяжка), материала крепежных деталей (углеродистая или легированная сталь) и их номинальных диаметров.

Ориентировочно при статической нагрузке крепежных деталей из углеродистых сталей: для незатянутых соединений [s]=1,5. 2 (в общем машиностроении), [s] = 3. 4 (для грузоподъемного оборудования); для затянутых соединений [s]=1,3. 2 (при контролируемой затяжке), [s]=2,5. 3 (при неконтролируемой затяжке крепежных деталей диаметром более 16 мм).

Для крепежных деталей с номинальным диаметром менее 16мм верхние пределы значений коэффициентов запаса прочности увеличивают в два и более раз ввиду возможности обрыва стержня из-за перетяжки.

Для крепежных деталей из легированных сталей (применяемых для более ответственных соединений) значения допускаемых коэффициентов запаса прочности берут примерно на 25% больше, чем для углеродистых сталей.

При переменной нагрузке значения допускаемых коэффициентов запаса прочности рекомендуются в пределах [s] = 2,5…4, причем за предельное напряжение принимают предел выносливости материала крепежной детали.

В расчетах на срез при переменной нагрузке значения допускаемых напряжений берут в пределах [τ_ср]=(0,2…0,3)σ_т (меньшие значения для легированных сталей).

Источник

Оформление и защита курсовых работ

Расчёт на прочность резьбовых соединений

Осевая нагрузка винта передаётся через резьбу гайке и уравновешивается реакцией её опоры. Каждый из Z витков резьбы нагружается силами F1, F2, … FZ.

В общем случае нагрузки на витках не одинаковы. Задача о распределении нагрузки по виткам статически неопределима и была решена русским учёным Н.Е. Жуковским в 1902 г. на основе системы уравнений для стандартной шестигранной гайки. График показывает значительную перегрузку нижних витков и бессмысленность увеличения длины гайки, т.к. последние витки практически не нагружены. Такое распределение нагрузки позже было подтверждено экспериментально. При расчётах неравномерность рагрузки учитывают эмпирическим (опытным) коэффициентом Km, который равен 0,87 для треугольной, 0,5 – для прямоугольной и 0,65 для трапецеидальной резьбы.

для расчёта крепёжных резьб – прочность по касательным напряжениям среза, а для ходовых резьб – износостойкость по напряжениям смятия.

Условие прочности на срез:

F / (πd1HKKm) ≤ [τ] для винта; τ = F / (πdHKKm) ≤ [τ] для гайки,

где H –высота гайки или глубина завинчивания винта в деталь, K=ab/p или K=ce/p – коэффициент полноты резьбы, Km – коэффициент неравномерности нагрузки по виткам.

Условие износостойкости на смятие:

s см = F / (πd2HZ) ≤ [ s ]см,

где Z – число рабочих витков.

Равнопрочность резьбы и стержня винта является важнейшим условием назначения высоты стандартных гаек. Так, приняв в качестве предельных напряжений пределы текучести материала и учитывая, что τТ ≈ 0,6 s Т условие равнопрочности резьбы на срез и стержня винта на растяжение предстанет в виде: τ = F/(πd1HKKm)= = 0,6σТ = 0,6 F /[(π/4) d12]. При K = 0,87 и Km = 0,6 получаем H ≈ 0,8d1, а учитывая, что d1 = d окончательно принимаем высоту нормальной стандартной крепёжной гайки H ≈ 0,8d.

Кроме нормальной стандартом предусмотрены высокие H ≈ 1,2d и низкие H ≈ 0,5d гайки. По тем же соображениям устанавливают глубину завинчивания винтов и шпилек в детали: в стальные H1 = d, в хрупкие – чугунные и силуминовые H =1,5d. Стандартные высоты гаек (кроме низких) и глубины завинчивания избавляют нас от расчёта на прочность резьбы стандартных крепёжных деталей.

В расчётах невозможно игнорировать податливость болта и соединяемых деталей. В простейшем случае при болтах постоянного сечения и однородных деталях

λб = lб / (Еб Аб); λд = δд / (Ед Ад),

В сложном случае податливость системы определяют как сумму податливостей отдельных участков болта и отдельных деталей. Под площадями сечения A понимают площади тех частей, которые подвержены деформации от затяжки болта. Здесь полагают, что деформации от гайки и головки болта располагаются вглубь деталей по конусам с углом α = 30о. Приравнивая объём этих конусов к объёму цилиндра, находят его диаметр

D1 = D +(δ1+ δ2) / 4; Aд = π (D12– dотв2) / 4.

Внешняя нагрузка F деформирует не только болт, но и прокладки, шайбы, тарельчатые пружины и т.п. (1,2). Поэтому при расчёте суммарной нагрузки болта FΣ вводят понятие коэффициента внешней нагрузки χ, равного приращению нагрузки болта в долях от внешней нагрузки. Тогда
FΣ = Fзат + χF. При этом упругие прокладки 1 и 2 нельзя рассматривать как детали 3, 4 и 5, деформация которых уменьшается. В таких случаях все детали соединения разделяют на две системы:

Детали системы болта, в которых под действием нагрузки абсолютная деформация возрастает (болт, прокладки 1,2);

Детали системы корпуса, в которых абсолютная деформация уменьшается (3,4,5).

При этом

В таких соединениях наборы упругих прокладок (шайб, тарельчатых пружин) существенно увеличивают податливость системы болта, а следовательно, уменьшают нагрузку на болт.

В расчёте болтов сначала находят силу, приходящуюся на один болт. Затем всё многообразие компоновок резьбовых соединений может быть сведено к трём простейшим расчётным схемам.

А. Болт вставлен в отверстия с зазором.

Соединение нагружено продольной силой Q. Болт растянут.

Условие прочности на растяжение запишется в виде:

Напряжения растяжения в резьбе

Из условия прочности на растяжение находим внутренний диаметр резьбы болта

Найденный внутренний диаметр резьбы округляют до ближайшего большего по ГОСТ 9150-59. Там же указан конкретный типоразмер-номер (наружный диаметр резьбы) болта.

Б. Болт вставлен в отверстия без зазора.

Соединение нагружено поперечной силой Р.

При этом болт работает на срез. Внутренний диаметр резьбы рассчитывается аналогично случаю с растяжением:

Порядок назначения номера болта также аналогичен предыдущему случаю.

В. Болт вставлен с зазором.

Соединение нагружено поперечной силой F.

Сила затяжки болта V должна дать такую силу трения между деталями, которая была бы больше поперечной сдвигающей силы F.

Болт работает на растяжение, а от момента затяжки испытывает ещё и кручение, которое учитывается повышением нормальных напряжений на 30% (в 1,3 раза).

Тогда

По опыту многочисленных расчётов принимают величину требуемой растягивающей силы V в зависимости от сдвигающей поперечной силы F

Тогда внутренний диаметр резьбы болта

где f – коэффициент трения.

Во всех случаях в расчёте находится внутренний диаметр резьбы, а обозначается резьба по наружному диаметру. Распространённая ошибка состоит в том, что рассчитав, например, внутренний диаметр резьбы болта 8мм, назначают болт М8, в то время как следует назначить болт М10, имеющий наружный диаметр резьбы 10мм, а внутренний 8мм.

Концентрация напряжений во впадинах витков резьбы учитывается занижением допускаемых напряжений резьбы на 40% по сравнению с соответствующими допускаемыми напряжениями материала.

Источник

2.7.2. Расчет резьбы на срез и смятие*

При действии на винт осевой силы условие прочности выглядит так:

ι и· Μ —допускаемое напряжение (см. § 2.3).

1’акой простейший случай нагружения in фсчается довольно редко (например, резъбо- м’>и участок крюка грузоподъемной машины ).

Прии действии на винт осевой силы F_iST и момента Т_р. что место во всех затянутых резьбовых соединениях (рис. 2.14),реже возникают нормальные и касательные напряжения.

1 1 ном случае для определения эквивалентных напряжений σ _F π ι > ι ι ΐΜ м ι iccTBCHHo применяют энергетическую теорию прочности

W_p = Ttd \ j \ b — момент сопротивления кручению. Если в форму­лу (2.8) подставить приведенные зависимости, то после преобра­зований получаем

Геометрическое подобие резьб позволяет приближенно при­нять d ₂ fd ₃ = 1,1, ψ = 2°30′ и / _S =0, I 5 (что соответствует ψ ] « 8°30 F ). С учетом этих значений

При проектном расчете диаметр dj можно определить из (2.9):

2.7.2. Расчет резьбы на срез и смятие*

Расчет витков резьбы на срез и смятие производят в случаях, когда одна из деталей, с резьбой выполнена из материала менее прочного, чем другая, или при использовании резьбовых деталей с нестандартными параметрами.

Таким образом, для резьбы винта F

коэффициент, учитывающий неравномерность распределения но ρ ν i к и по виткам резьбы с учетом пластических деформаций в «те наиболее нагруженных витков (для резьб с крупным ша-

Источник

Расчет резьбы на прочность

Основные виды разрушения резьб: крепежных — срез витков, ходовых — износ витков. В соответствии с этим основными критериями работоспособности и расчета для крепежных резьб являются прочность, связанная с напряжениями среза t, а для ходовых резьб — износостойкость, связанная с напряжениями смятия s _см, рис. 1.17.

Условия прочности резьбы по напряжениям среза:

для винта,

для гайки(1.12)

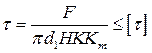
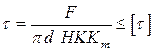
где H — высота гайки или глубина завинчивания винта в деталь; К = аb/р или К = се/р — коэффициент полноты резьбы; К_m — коэффициент неравномерности нагрузки по виткам резьбы.

Если материалы винта и гайки одинаковы, то по напряжениям среза рассчитывают только резьбу винта, так как d₁

где z = H/p — число рабочих витков (например, число витков гайки). Формула (1.13)—общая для винта и гайки. Коэффициент К_m здесь принят равным единице, с учетом приработки ходовых резьб и при условии, что допускаемые напряжения принимают согласно с накопленным опытом эксплуатации.

Высота гайки и глубина завинчивания. Равнопрочность резьбы и стержня винта является одним из условий назначения высоты стандартных гаек.

Так, например, приняв в качестве предельных напряжений пределы текучести материала на растяжение и сдвиг и учитывая, что t_T = 0,6 s_T,

запишем условия равнопрочности резьбы на срез и стержня винта на растяжение в виде:

F/[(p/4)d₁ 2 ] — напряжение растяжения в стержне винта, рассчитанное приближенно по внутреннему диаметру резьбы d₁. откуда при K = 0,87 и K_m » 0,6 получаем:

В соответствии с этим высоту нормальных стандартных гаек крепежных изделий принимают H » 0,8d. (1.15)

Кроме нормальных стандартом предусмотрены высокие H » 1,2 d низкие H » 0,5 d гайки.

Так как d > d₁ (например, для основной крепежной резьбы d » 1,2 d₁, то прочность резьбы при нормальных и высоких гайках превышает прочность стержня винта.

По тем же соображениям устанавливают глубину завинчивания винтов и шпилек в детали: в стальные детали H₁ = d, в чугунные и силуминовые H₁ » 1,5d.

Стандартные высоты гаек (за исключением низких) и глубины завинчивания исключают необходимость расчета на прочность резьбы стандартных крепежных деталей

Расчет на прочность стержня винта (болта) при различных случаях нагружения

Стержень винта нагружен только внешней растягивающей силой. Примером служит нарезанный участок крюка для подвешивания груза (рис. 1.18). Опасным является сечение, ослабленное нарезкой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d₁ резьбы. Условие прочности по напряжениям растяжения в стержне:

Болт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин (рис. 1.19). В этом случае стержень болта растягивается осевой силой F_зат возникающей от затяжки болта, и закручивается моментом сил в резьбе Т_р—см. формулу (1.5), где F равна Fзат. Напряжение растяжения от силы F_зат, Напряжение кручения от момента Т_Р : Требуемое значение силы затяжки

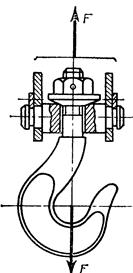
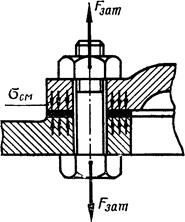
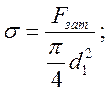
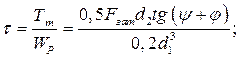
Прочность болта определяют по эквивалентному напряжению: 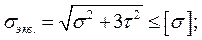(1.18)

Вычисления показывают, что для стандартных метрических резьб, s_экв= 1,3 s.

Это позволяет рассчитывать прочность болтов по упрощенной формуле:

Поэтому в среднем и тяжелом машиностроении не рекомендуют применять болты малых диаметров (меньше М8). На некоторых заводах для затяжки болтов используют специальные ключи предельного момента. Эти ключи не позволяют приложить при затяжке момент больше установленного. В таком случае отпадает необходимость ограничивать применение болтов малых диаметров (при условии, что ключи предельного момента применяют и в эксплуатации).

Болтовое соединение нагружено силами, сдвигающими детали в стыке

Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах. Болт поставлен с зазором (рис. 1.20). При этом внешнюю нагрузку F уравновешивают силами трения в стыке, которые образуются от затяжки болта. Без затяжки болтов детали могут сдвигаться на значение зазора, что не допустимо. Рассматривая равновесие детали 2, получим условие отсутствия сдвига деталей

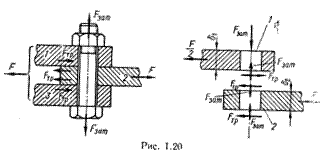
F £ iF_TP = iF_зат f, илиF_зат = K F / ( i f );

Прочность болта оценивают по эквивалентному напряжению — формула (1.19).

Отметим, что в соединении, в котором болт поставлен с зазором. внешняя нагрузка не передается на болт. Поэтому болт рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных значений коэффициента запаса.

Болт поставлен без зазора (рис. 1.21).

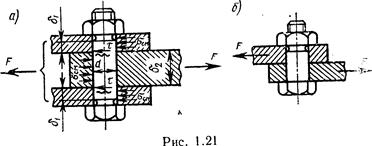
В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности соединения не учитывают силы трения в стыке, так как затяжка болта необязательна. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия.

Условие прочности по напряжениям среза:

(1.21), где i — число плоскостей среза (на рис. 1.21a, i = 2; при соединении только двух деталей — рис. 1.21, б i = 1). Закон распределения напряжений смятия по цилиндрической поверхности контакта болта и детали (рис. 1.22) трудно установить точно.

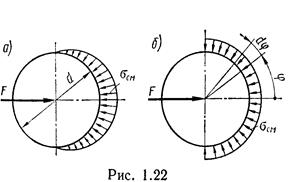
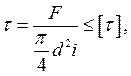
В значительной степени это зависит от точности размеров и формы деталей соединения. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рис. 1.22, а) заменяют условной с равномерным распределением напряжений (рис. 1.22, б).

При этом для средней детали (и при соединении только двух деталей)

или 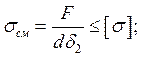для крайней детали

Формулы (1.22) справедливы для болта и деталей. Из двух значений s_cм в этих формулах расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали.

Сравнивая варианты установки болтов с зазором и без зазора (см. рис. 1.20 и 1.21), следует отметить, что первый вариант дешевле второго, так как не требует точных размеров болта и отверстия. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора.

Так, например, приняв коэффициент трения в стыке деталей f » 0,2, K=1,5 и i = 1, из формулы (1.20) получим F_зат= 7,5F. Следовательно, расчетная нагрузка болта с зазором в 7,5 раз превышает внешнюю нагрузку. Кроме того, вследствие нестабильности коэффициента трения и трудности контроля затяжки работа таких соединений при сдвигающей нагрузке недостаточно надежна.

Болт затянут, внешняя нагрузка раскрывает стык деталей

Примером служат болты для крепления крышек резервуаров, нагруженных давлением p жидкости или газа (рис. 1.23). Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Задача о распределении нагрузки между элементами такого соединения статически неопределима и решается с учетом деформаций этих элементов. Обозначим: F_зат — сила затяжки болта; F=R/z — внешняя нагрузка соединения, приходящаяся на один болт (z — число болтов).

После приложения внешней нагрузки к затянутому соединении; болт дополнительно растянется на некоторую величину D, а деформация сжатия деталей уменьшится на ту же величину.

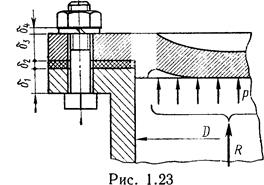
Для простоты можно сказать, что только часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку стыка.

Если обозначим c — коэффициент внешней нагрузки (учитывает; приращение нагрузки болта в долях от силы F, то дополнительна нагрузка болта равна c F, а уменьшение затяжки стыка — (1—c)F

Значение коэффициента c определяют по условию равенства дополнительных деформаций болта и деталей (условие совместности деформаций):

(1.23);

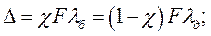
где l_б — податливость болта, равная его деформации при единично нагрузке; l_д — суммарная податливость соединяемых деталей.

(1.24)

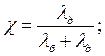
Далее получим приращение нагрузки на болт

(1.25)

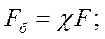
расчетную (суммарную) нагрузку болта

(1.26)

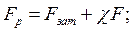
и остаточную затяжку стыка от одного болта

(1.27)

Источник